Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Chimie-Physique | |||||||
Le but de ce chapitre n’est pas de se lancer dans la chimie au sens strict, mais d’aborder la chimie physique. Celle-ci tente d’expliquer la structure électronique des divers éléments, qui permet à son tour de comprendre :
Les deux premiers domaines intéressent l’astronomie, le premier pour l’étude des molécules qui se forment dans les atmosphères froides de certaines étoiles, dans celles des planètes ou dans leur sol, ou encore dans le milieu interstellaire ; le second par l’importance capitale que représente la spectroscopie dans l’étude de tous les astres. Le tableau de Mendeleev enfin, est l’outil fondamental de l’étude des éléments. Il résume une grande partie de leurs propriétés.
Les éléments qui sont dans une même colonne possèdent des propriétés chimiques très semblables, et forment une famille. Ainsi, la colonne de gauche est celle des alcalins : Li, Na, K, Rb, Cs, Fr. La colonne de droite est celle des gaz rares ou gaz nobles : He, Ne, Ar, Kr, Xe, Ra. L’avant-dernière à droite celle des halogènes : F, Cl, Br, I, At.
Les lignes de ce tableau représentent des périodes.
Les atomes sont attachés les uns aux autres, dans les molécules chimiques, par la force électromagnétique. Pour comprendre la chimie, il faut donc étudier les propriétés électroniques des atomes.
L’énergie d’ionisation est la première notion importante. Lorsqu’un atome est neutre, son noyau est entouré d’un nombre d’électrons égal à son nombre de protons, et ces électrons sont liés par la force électromagnétique. Mais cette force est limitée, et l’atome peut perdre un ou plusieurs électrons. Tout dépend de l’énergie disponible. Plus un électron est lié fortement, plus il faut d’énergie pour l’arracher à son atome. Et cette énergie se mesure. Un atome ayant en général plusieurs électrons (sauf l’hydrogène), les divers électrons n’ont pas le même comportement. On utilise le modèle en couches, dans lequel les électrons se répartissent selon des niveaux d’énergie, correspondant à des orbitales autour du noyau. L’électron sur l’orbitale la plus externe est le plus susceptible de quitter l’atome, l’énergie nécessaire pour cela est nommée énergie de première ionisation. Pour l’hydrogène, l’énergie de première ionisation est de 13,6 eV (il n’y en a pas d’autres, puisque l’hydrogène n’a qu’un seul proton).
L’énergie d’ionisation est toujours positive : pour arracher un électron lié à son atome, il faut en fournir.Lorsqu’un premier électron a été arraché, un second peut être enlevé à son tour. Il faut pour cela disposer de l’énergie de seconde ionisation. Pour la chimie, l’énergie de première ionisation joue un rôle important : elle détermine la capacité d’un atome à perdre un électron.
Réciproquement, un atome peut gagner un électron. Si son cortège électronique n’est pas complet, l’acquisition d’un électron s’accompagne de l’émission d’une énergie égale à celle nécessaire pour arracher l’électron. Cette énergie est sous la forme d’un photon, d’énergie bien précise, et elle donne lieu à une raie d’émission.
Un atome peut-il acquérir plus d’électrons qu’il n’a de protons ? Oui, car en fait il crée autour de lui un champ électromagnétique positif, qui attire les électrons sans distinction. La limitation vient de la répulsion que les électrons produisent entre eux. Mais dans certains cas, le nombre d’électrons peut donc dépasser le nombre de protons. On a alors ce qu’on appelle un ion négatif (lorsqu’on arrache des électrons à un atome, on obtient un ion positif).
Si un atome gagne un électron en plus de son quota (égal au nombre de protons), cet ajout se fait avec un échange d’énergie, nommée énergie d’attachement. Mais alors que l’énergie d’ionisation est toujours positive, l’énergie d’attachement peut être positive ou négative. Ceci a une grande importance : un système physique, quel qu’il soit, tend toujours à se placer dans son état d’énergie minimale. Par conséquent, si l’état de l’atome avec un électron en plus est moins énergétique que son état avec le nombre standard d’électrons (égal au nombre de protons), alors l’ion négatif est plus stable que l’atome neutre.
Les atomes qui sont dans ce cas sont donc plus stables s’ils ont un électron en plus ! Et cet électron, ils pourraient le prendre à un autre atome… pourvu que ce dernier soit dans la situation inverse, c’est-à-dire que son état neutre soit plus stable.
L’énergie d’attachement correspond à l’énergie échangée lors de l’attachement du premier électron supplémentaire. Cette notion est symétrique de l’énergie de première ionisation
Cette nouvelle notion est dérivée de la précédente, c’est l’électronégativité. Elle compare l’énergie d’ionisation (faculté de perdre un électron), à l’énergie d’attachement (faculté d’en gagner un). Il y a deux définitions différentes de l’électronégativité, qui donnent le même classement des éléments chimiques. Nous en choisirons une, celle de Mulliken pour des raisons de simplicité. Elle définit l’électronégativité comme la moyenne arithmétique de l’énergie d’ionisation et de l’énergie d’attachement. Cette moyenne est une énergie. Or l’électronégativité est simplement une tendance à acquérir ou perdre des électrons. Mulliken a donc multiplié cette moyenne par une constante exprimée en eV-1. Ainsi, le produit n’a pas d’unité :
L’électronégativité représente le comportement chimique des éléments. Ainsi, leur caractère réducteur ou oxydant lui est lié :
Dans le tableau de Mendeleev, l’électronégativité croît de la gauche vers la droite : les alcalins (colonne de gauche) sont peu électronégatifs ; les halogènes (avant-dernière colonne à droite) le sont fortement. Verticalement, l’électronégativité croît de bas en haut.
Prenons le fluor en exemple. C’est un oxydant très puissant. Il se trouve en haut et à droite du tableau de Mendeleev. Son électronégativité de Mulliken est la plus élevée, et vaut 3,90. A l’inverse, le rubidium a une électronégativité de Mulliken de 0,50 seulement. Il est tout à gauche dans le tableau de Mendeleev, dans la colonne des alcalins. Il est très réducteur.
Pour qu’une réaction chimique se produise, il faut que des molécules se rencontrent. Certaines réactions mettent en jeu un grand nombre de molécules. Si c’était la réalité physique, la probabilité qu’elles se produisent serait infiniment faible, puisqu’elle nécessiterait la rencontre simultanée de toutes ces molécules. En fait, les réactions très probables sont celles qui ne mettent en jeu que deux molécules. Les réactions à trois molécules peuvent encore se produiren beaucoup plus rarement. Pour un nombre plus grand, la probabilité est si faible que le taux de réaction est totalement négligeable.
Il faut alors admettre que ce que nous voyons en observant les réactifs d’une part, et les produits de l’autre (c’est-à-dire avant et après la réaction), ne décrit pas ce qu’il se passe dans le réacteur (pendant). La réaction ne se produit en général pas comme on la décrit, mais elle est la somme d’une suite de réactions plus simples, que l’on appelle réactions élémentaires.
Par analogie, vous pouvez considérer en physique nucléaire la chaîne proton-proton, qui s’écrit globalement 4 1H → 4He, mais qui est en fait une succession de réactions élémentaires. La probabilité que 4 protons donnent directement un noyau d’hélium est infiniment petite.
La vitesse de réalisation d’une réaction est donc conditionnée par la plus lente des réactions élémentaires qui la constituent. Aussi, pour calculer cette vitesse est-il nécessaire d’analyser la réaction.
Nous avons vu les propriétés optiques de l’atome d’hydrogène dans le chapitre consacré à la lumière. Pour expliquer les raies d’émission (ou d’absorption), on a utilisé un nombre entier qui définit des niveaux d’énergie ; lorsque l’électron change de niveau d’énergie, il émet ou absorbe un photon d’énergie correspondant à la différence entre les deux niveaux. Si la différence est négative, il émet un photon, sinon il l’absorbe. L’atome d’hydrogène possèdant un unique proton, on conçoit que ses propriétés soient plus simples que celles des autres, et c’est d’ailleurs pourquoi il a été pris comme premier sujet d’étude, et comme exemple.
Le nombre entier défini pour l’atome d’hydrogène est appellé nombre quantique principal, et il est noté n.
L’extrapolation de ce modèle simple aux autres atomes ne donne pas de résultats en accord avec l’expérience. Un niveau d’énergie, définit par le nombre n, peut accueillir deux électrons, de spins opposés. Pas plus. Donc, en extrapolant ce raisonnement pour des noyaux lourds, le second niveau d’énergie ne doit contenir que 2 électrons. Or ceci est contredit par la spectroscopie : le second niveau d’énergie accueille 8 électrons !
Comment concilier le modèle de l’atome d’hydrogène, qui le décrit si bien, avec ce résultat incompatible ? Les principes utilisés pour l’hydrogène sont : quantification de l’énergie (par le nombre n), et principe d’exclusion qui interdit que deux électrons soient dans le même état. Le spin permet d’avoir deux électrons au même niveau d’énergie. Pour en accepter plus sur un même niveau, en conservant ces idées, il est assez naturel d’introduire un nouveau nombre quantique, qui permettra de différencier des états sans lui semblables.
On a donc introduit le nombre quantique azimutal, noté l. Physiquement, il correspond à l’opérateur de moment angulaire, et donc à la forme des orbitales. Ceci impose une contrainte sur ses valeurs.
Enfin, pour tenir compte de certains effets, comme l’effet Zeeman (dédoublement magnétique des raies spectrales), on doit introduire un dernier nombre, nommé nombre quantique magnétique, et noté ml. Il représente l’orientation de l’atome dans l’espace. Le nombre quantique magnétique doit, lui aussi, satisfaire à des contraintes déduites de la théorie.
L’état d’un électron est donc totalement décrit par les 4 nombres quantiques suivants :
| nombre quantique principal | n | n ≥ 1 |
| nombre quantique azimutal | l | 0 ≤ l ≤ n - 1 |
| nombre quantique magnétique | ml | -l ≤ ml ≤ +l |
| nombre quantique de spin | ms | ms = -1/2 ou ms = +1/2 |
Lorsqu’une orbitale est peuplée par deux électrons, ceux-ci, pour respecter le principe d’exclusion, doivent obligatoirement être de spins opposés. On dit qu’ils sont apariés. Si un électron se trouve seul sur son orbitale, on le dit célibataire. Electrons célibataires et apariés jouent des rôles différents dans les liaisons chimiques.
En ne considérant tout d’abord que le nombre quantique principal n, on obtient les couches électroniques. Elles prennent pour nom une lettre majuscule, en commençant par K :
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| symbole | K | L | M | N | O | P | Q |
Prenant ensuite en compte le nombre quantique azimutal (en conjonction avec n), on définit la notion de sous-couche. Pour chaque couche n, il y a une sous-couche par valeur différente de l. Les sous-couches sont nommées par une lettre minuscule, attachée au nombre quantique azimutal :
| l | 0 | 1 | 2 | 3 | 4 |
| sous-couche | s | p | d | f | g |
La signification des lettres, provenant de la spectroscopie, est la suivante : s = sharp ; p = principal ; d = diffuse ; f = fondamental. Pour la suite, il n’y a plus de signification particulière, et on prend simplement les lettres suivantes dans l’ordre alphabétique : g, h, i…
La caractérisation complète d’une sous-couche fait apparaître le nombre quantique principal n et le nombre quantique azimutal, le premier précédant l’autre exprimé par sa lettre. Ainsi, on aura les sous-couches 1s, 2s, 2p, 3d… Le tableau ci-dessous tient compte de la contrainte qui pèse sur l (0 ≤ l ≤ n - 1) pour définir les sous-couches possibles :
| n \ l | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 1 | 1s | ||||
| 2 | 2s | 2p | |||
| 3 | 3s | 3p | 3d | ||
| 4 | 4s | 4p | 4d | 4f | |
| 5 | 5s | 5p | 5d | 5f | 5g |
Toute sous-couche est donc caractérisée par un couple (n, l), formé par les deux premiers nombres quantiques : 1s : (1, 0) ; 2s : (2, 0) ; 2p : (2, 1) ; 3s : (3, 0) ; 3p : (3, 1) ; 3d : (3, 2) ; etc.
Les sous-couches représentent la possibilité d’accueillir un (ou plusieurs) électron(s). Elles peuvent être vides, ou en partie pleines. Si elles le sont en totalité, on dira qu’elles sont saturées. Il est important d’indiquer le nombre d’électrons qui peuplent effectivement une sous-couche. Ceci se fait en indiquant ce nombre en exposant à droite de la désignation de la couche. Ainsi, 1s1 indique que la couche 1s contient 1 électron. 1s2 indique qu’elle en contient 2, elle est alors saturée. Lorsqu’on précise l’état d’un atome, on indique toutes les couches partiellement ou totalement remplies, et on omet les vides.
Les sous-couches représentent les niveaux d’énergie. Pour une même valeur de n, il y a autant de niveaux d’énergie que de sous-couches, c’est-à-dire autant que de valeurs différentes de l soit n valeurs (puisque 0 ≤ l ≤ n - 1). Un niveau d’énergie, pour les atomes plus lourds que l’hydrogène, est donc défini par le couple (n, l). Pour le niveau n, ce sont donc les couples (n, 0), (n, 1), … (n, n-1).
Pour l’atome d’hydrogène, nous avons parlé d’orbite de l’électron, et pour être plus correct dans le langage de la Mécanique Quantique, d’orbitale. L’électron est sur une orbitale, et en change par émission ou absorption de photons. Dans ce cadre, nous avons toujours confondu orbitale et niveau d’énergie. C’est possible, car l’atome d’hydrogène est le plus simple. Mais pour les autres atomes, il convient de bien distinguer : à un niveau d’énergie correspondent en général plusieurs orbitales, distinguées par leur nombre quantique magnétique (leur orientation dans l’espace).
La caractérisation complète d’une orbitale fait donc intervenir les trois premiers nombres quantiques, et correspond au triplet (n, l, ml). La contrainte de définition de ml étant -l ≤ ml ≤ +l, la table ci-dessous donne toutes les orbitales pour les couches K, L, M et N (n = 1, 2, 3, 4).
| couches | sous-couches / orbitales | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 1s | |||||||||||||||
| (1, 0, 0) | ||||||||||||||||
| L | 2s | 2p | ||||||||||||||
| (2, 0, 0) | (2, 1, -1) | (2, 1, 0) | (2, 1, +1) | |||||||||||||
| M | 3s | 3p | 3d | |||||||||||||
| (3, 0, 0) | (3, 1, -1) | (3, 1, 0) | (3, 1, +1) | (3, 2, -2) | (3, 2, -1) | (3, 2, 0) | (3, 2, +1) | (3, 2, +2) | ||||||||
| N | 4s | 4p | 4d | 4f | ||||||||||||
| (4, 0, 0) | (4, 1, -1) | (4, 1, 0) | (4, 1, +1) | (4, 2, -2) | (4, 2, -1) | (4, 2, 0) | (4, 2, +1) | (4, 2, +2) | (4, 3, -3) | (4, 3, -2) | (4, 3, -1) | (4, 3, 0) | (4, 3, +1) | (4, 3, +2) | (4, 3, +3) | |
Les couches K, L, etc sont indiquées à gauche. Les sous-couches sont notées dans les cellules du haut de chaque couche (1s, 2s, 2p, etc). Enfin, les orbitales sont données par les triplets qui les représentent.
Le dernier nombre quantique, le spin, intervient maintenant. Sur chaque orbitale, l’atome peut accueillir 2 électrons et non un seul,à la condition que leurs spins soient différents. L’état complet d’un électron est donc défini, finalement, par les 4 nombres quantiquesnotés par un quadruplet tel par exemple (4, 3, -2, +1/2) ou (4, 3, -2, -1/2). On peut alors déterminer le nombre d’électrons par couches : 2 pour K, 8 pour L, 18 pour M, 32 pour N… Les parties grisées du tableau sont vides, car elles sont en-dehors des contraintes sur les nombres quantiques. Par exemple, pour la couche K (n = 1), l ≤ n - 1 implique que l ne peut prendre que la seule valeur 0.
Toutes les orbitales qui sont dans la même sous-couche ont le même niveau d’énergie. Dans chaque cellule du tableau, on devrait remplacer le triplet (n, l, ml) par les deux quadruplets (n, l, ml, s), où s prend les valeurs +1/2 et -1/2. Ainsi, chaque cellule du tableau représente au plus deux électrons. La sous-couche 3p par exemple peut contenir jusqu’à 3 × 2 = 6 électrons.
Un atome peut être totalement ionisé, c’est-à-dire avoir perdu la totalité de ses électrons. Il suffit pour cela qu’il soit plongé dans un milieu assez chaud. Si la température baisse alors, il va capturer un électron, puis un second… Le premier électron ira tout naturellement dans le niveau d’énergie fondamental, qui correspond à l’énergie minimale. Le second ira dans la première sous-couche disponible (ce sera la même que pour le premier si le spin peut les différencier). Ainsi, le remplissage se fait par ordre d’énergie de liaison croissante, de l’orbitale la plus liée à la moins liée (principe d’aufbau = construction). Ceci est tout à fait normal. Mais la difficulté vient du fait que cet ordre ne correspond pas exactement à l’ordre lexicographique des sous-couches (ordre des nombres quantiques croissants que nous avons utilisé jusque-là).
L’ordre qui semble naturel est celui dans lequel on a tendance à les écrire, par n croissant, et par l croissant en cas d’égalité de n. Mais il ne correspond pas à l’ordre des énergies décroissantes. Par exemple, la sous-couche 4s possède une énergie plus élevée que la sous-couche 3d ! Ainsi, elle sera remplie avant. Klechkowski a proposé une règle facile à retenir :
Ecrivons d’abord les sous-couches dans l’ordre naturel, en plaçant en-dessous la somme n + l :
| sous-couche | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| état (n, l) | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (3, 2) | (4, 0) | (4, 1) | (4, 2) | (4, 3) | (5, 0) | (5, 1) | (5, 2) | (5, 3) | (5, 4) |
| n + l | 1 | 2 | 3 | 3 | 4 | 5 | 4 | 5 | 6 | 7 | 5 | 6 | 7 | 8 | 9 |
Entre 2p et 3s, la somme ne change pas. La règle indique qu’il faut choisir le n minimum, et cela correspond à l’ordre naturel.
Entre 3d et 4s, la somme décroît. La règle impose donc de permutter ces deux sous-couches, ce qui correspond à l’énergie croissante. On doit alors comparer 3d et 4p, ce qui revient à conserver cet ordre, puisqu’il est celui des n croissants.
| sous-couche | 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| état (n, l) | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (4, 0) | (3, 2) | (4, 1) | (4, 2) | (4, 3) | (5, 0) | (5, 1) | (5, 2) | (5, 3) | (5, 4) |
| n + l | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 5 | 6 | 7 | 8 | 9 |
La couche 5s, de somme 5, doit rétrograder de deux places.
| sous-couche | 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | 5s | 4d | 4f | 5p | 5d | 5f | 5g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| état (n, l) | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (4, 0) | (3, 2) | (4, 1) | (5, 0) | (4, 2) | (4, 3) | (5, 1) | (5, 2) | (5, 3) | (5, 4) |
| n + l | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 | 7 | 6 | 7 | 8 | 9 |
On doit permuter 4f et 5p :
| sous-couche | 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | 5s | 4d | 5p | 4f | 5d | 5f | 5g |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| état (n, l) | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (4, 0) | (3, 2) | (4, 1) | (5, 0) | (4, 2) | (5, 1) | (4, 3) | (5, 2) | (5, 3) | (5, 4) |
| n + l | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 9 |
Maintenant, les sous-couches que nous avons considérées sont dans l’ordre de remplissage qui correspond à l’ordre des énergies décroissantes (en valeur absolue), jusqu’à 5p. En effet, la somme n + l pour 5p est 5 + 1 = 6, et celle de 6s, que nous n’avons pas représentée dans le tableau, vaut 6 + 0 = 6 également. Elle va donc venir après 5p, puisque son n est supérieur, et immédiatement après puisque les suivants sont plus élevés :
| sous-couche | 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | 5s | 4d | 5p | 6s | 4f | 5d | 5f |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| état (n, l) | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (4, 0) | (3, 2) | (4, 1) | (5, 0) | (4, 2) | (5, 1) | (6, 0) | (4, 3) | (5, 2) | (5, 3) |
| n + l | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 8 |
Maintenant, le tableau est dans l’ordre jusqu’à 5f. On peut imaginer comment ordonner la suite, sans même écrire la suite du tableau. On construit un graphe de remplissage :
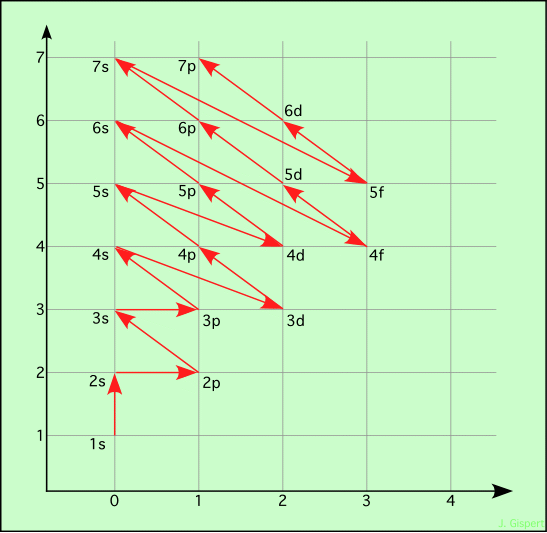
Comme on le constate, le remplissage est loin d’être aussi simple qu’on pouvait le supposer a priori. Mais la règle de Klechkowski est d’application aisée, et donne facilement la solution.
Remarquez que, historiquement, le schéma a été construit sur les données expérimentales, et la règle de Klechkowski en a été déduite. Elle se voit très clairement par le parcours : n a tendance à augmenter globalement. Lorsque ce n’est pas le cas, c’est l qui augmente. Il est assez facile de constater que leur somme est vraiment croissante. Et les seuls cas où elle est stationnaire, n augmente.
On doit maintenant se demander comment les électrons peuplent les différentes sous-couches. Les sous-couches s sont caractérisées par l = 0, donc -l ≤ ml ≤ +l devient -0 ≤ ml ≤ +0, donc une seule orbitale correspondant à ml = 0. Mais les autres sous-couches se décomposent en plusieurs orbitales, puisque pour elles des valeurs > 0 sont possibles.Comment les électrons vont-ils peupler ces orbitales ? L’ordre défini par la règle de Klechkowski ne répond pas. Réécrivons le tableau ci-dessus, en remplaçant la somme n + l par le nombre d’électrons que la sous-couche peut accueillir (deux par orbitale, en respectant le principe d’exclusion naturellement).
| sous-couche | 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | 5s | 4d | 5p |
|---|---|---|---|---|---|---|---|---|---|---|---|
| état | (1, 0) | (2, 0) | (2, 1) | (3, 0) | (3, 1) | (4, 0) | (3, 2) | (4, 1) | (5, 0) | (4, 2) | (5, 1) |
| nombre d’orbitales (-l .. +l) | 1 | 1 | 3 | 1 | 3 | 1 | 5 | 3 | 1 | 5 | 3 |
| Nombre d’électrons | 2 | 2 | 6 | 2 | 6 | 2 | 10 | 6 | 2 | 10 | 6 |
| 1s | 2s | 2p | 3s | 3p | 4s | 3d | 4p | ||||||||||
| (1, 0, 0) | (2, 0, 0) | (2, 1, -1) | (2, 1, 0) | (2, 1, +1) | (3, 0, 0) | (3, 1, -1) | (3, 1, 0) | (3, 1, +1) | (4, 0, 0) | (3, 2, -2) | (3, 2, -1) | (3, 2, 0) | (3, 2, +1) | (3, 2, +2) | (4, 1, -1) | (4, 1, 0) | (4, 1, +1) |
| 5s | 4d | 5p | 6s | 4f | 5d … | ||||||||||||
| (5, 0, 0) | (4, 2, -2) | (4, 2, -1) | (4, 2, 0) | (4, 2, +1) | (4, 2, +2) | (5, 1, -1) | (5, 1, 0) | (5, 1, +1) | (6, 0, 0) | (4, 3, -3) | (4, 3, -2) | (4, 3, -1) | (4, 3, 0) | (4, 3, +1) | (4, 3, +2) | (4, 3, +3) | … |
Le tableau contient les différentes sous-couches dans l’ordre de remplissage vu plus haut. Les orbitales sont indiquées. Voyons comment elles se remplissent.
Pour cet élément, un problème se pose. Pour le cinquième électron, trois orbitales se présentent, toutes vides : les (2, 1, -1), (2, 1, 0) et (2, 1, +1). Laquelle sera occupée ? Les trois orbitales ne se distinguent que par leur orientation spatiale, et partagent exactement la même énergie. De ce fait, la probabilité d’occupation des trois orbitales est la même, et l’électron se place sur l’une quelconque des trois.
L’élément suivant est le carbone (Z = 6). Le sixième électron est placé devant un choix : soit occuper la même orbitale que le précédent, en ayant un spin opposé ; soit occuper une autre orbitale, les spins étant alors libres. Les spins tendent à se placer parallèles plutôt qu’antiparallèles (minimum d’énergie). Cette particularité donne lieu à la règle de Hund :
Parmi les configurations possibles, celle qui maximise le spin total (la somme des spins des électrons considérés) est celle qui minimise l’énergie. C’est ce qui justifie la règle de Hund. Les spins pouvant valoir +1/2 ou -1/2, c’est la configuration avec tous les spins +1/2 (si elle est possible), qui est celle de moindre énergie.
Un noyau tout seul produit dans son voisinage un champ électromagnétique de symétrie sphérique (à la distance à laquelle se trouvent normalement les électrons, la distribution des protons est pratiquement sphérique). Si un électron est autour du noyau, le champ est modifié : vu de l’extérieur, le champ négatif de l’électron masque le champ positif du noyau. Comme si un écran était intreposé, c’est pourquoi on nomme ce phénomène écrantage. Un second électron, plus loin du noyau, ressent donc un champ positif affaibli, et sa liaison au noyau s’en trouve affaiblie.
| couches | sous-couches / orbitales | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 1s | |||||||||||||||
| (1, 0, 0) | ||||||||||||||||
| L | 2s | 2p | ||||||||||||||
| (2, 0, 0) | (2, 1, -1) | (2, 1, 0) | (2, 1, +1) | |||||||||||||
| M | 3s | 3p | 3d | |||||||||||||
| (3, 0, 0) | (3, 1, -1) | (3, 1, 0) | (3, 1, +1) | (3, 2, -2) | (3, 2, -1) | (3, 2, 0) | (3, 2, +1) | (3, 2, +2) | ||||||||
| N | 4s | 4p | 4d | 4f | ||||||||||||
| (4, 0, 0) | (4, 1, -1) | (4, 1, 0) | (4, 1, +1) | (4, 2, -2) | (4, 2, -1) | (4, 2, 0) | (4, 2, +1) | (4, 2, +2) | (4, 3, -3) | (4, 3, -2) | (4, 3, -1) | (4, 3, 0) | (4, 3, +1) | (4, 3, +2) | (4, 3, +3) | |
On peut considérer cet ordre de remplissage pour un atome ionisé, qui récupère au fur et à mesure des électrons. Mais il est également l’ordre dans lequel les différents atomes remplissent leurs couches. Ainsi, l’hydrogène (un seul proton, Z = 1) reçoit son électron au niveau 1s. L’atome d’hydrogène neutre peut donc se représenter par 1s1, le 1 en exposant rappelant qu’il y a un électron.
Pour l’hélium, les deux électrons coexistent sur la couche 1s, avec leurs spins antiparallèles : +1/2 pour l’un, -1/2 pour l’autre. La représentation est : 1s2. Remarquez que l’hélium ionisé une fois est représenté par 1s1, comme l’hydrogène neutre. Plus généralement, tout atome ionisé auquel ne reste qu’un unique électron possède la même configuration électronique : 1s1. Ces ions sont nommés, pour cela, hydrogénoïdes.
Le lithium possède 3 protons (Z = 3), donc la première couche est saturée : 1s2. Il reste un électron à caser ; il ira dans la sous-couche 2s : 2s1. La notation complète pour le lithium sera donc : 1s22s1.
L’élément suivant, le berylium Be, possède 4 protons. Les deux premiers électrons iront saturer la sous-couche 1s, les deux autres trouveront leur place dans la sous-couche 2s, et seront naturellement antiparallèles (principe d’exclusion). Ensuite, le bore B possède 5 protons ; il aura la même configuration pour les 4 premiers électrons, et logera le cinquième dans une nouvelle sous-couche.
| 1H | 2He | 3Li | 4Be | 5B | 6C | 7N | 8O | 9F | 10Ne |
| 1s1 | 1s2 | 1s22s1 | 1s22s2 | 1s22s22p1 | 1s22s22p2 | 1s22s22p3 | 1s22s22p4 | 1s22s22p5 | 1s22s22p6 |
| 11Na | 12Mg | 13Al | 14Si | 15P | 16S | 17Cl | 18Ar |
| 1s22s22p63s1 | 1s22s22p63s2 | 1s22s22p63s23p1 | 1s22s22p63s23p2 | 1s22s22p63s23p3 | 1s22s22p63s23p4 | 1s22s22p63s23p5 | 1s22s22p63s23p6 |
La suite du remplissage serait fastidieuse, car on observe que la configuration électronique s’allonge de plus en plus. Mais on peut faire une remarque : on a rempli le tableau jusqu’au troisième gaz rare, l’argon. Et il apparaît que les éléments qui suivent chaque gaz rare reprennent la configuration électronique de ce dernier, en lui ajoutant de nouveaux électrons. Le premier gaz rare est l’hélium, 1s2. Tous les éléments, du lithium jusqu’au néon, ont leur configuration électronique qui commence comme celle de l’hélium. Alors, au lieu de répéter celle-ci, on note à sa place le symbole du gaz rare, mis entre crochets : la configuration du lithium est [He]2s1, celle du berylium [He]2s2, celle du bore [He]2s22p1, etc.
Il en est de même après les autres gaz rares. Ainsi, le sodium Na est représenté par [Ne]3s1, etc. on peut réécrire le tableau sous cette nouvelle forme, en le complétant :
| 1H | 2He | 3Li | 4Be | 5B | 6C | 7N | 8O | 9F | 10Ne |
| 1s1 | 1s2 | [He]2s1 | [He]2s2 | [He]2s22p1 | [He]2s22p2 | [He]2s22p3 | [He]2s22p4 | [He]2s22p5 | [He]2s22p6 |
| 11Na | 12Mg | 13Al | 14Si | 15P | 16S | 17Cl | 18Ar |
| [Ne]3s1 | [Ne]3s2 | [Ne]3s23p1 | [Ne]3s23p2 | [Ne]3s23p3 | [Ne]3s23p4 | [Ne]3s23p5 | [Ne]3s23p6 |
| 19K | 20Ca | 21Sc | 22Ti | 23V | 24Cr | 25Mn | 26Fe | 27Co |
| [Ar]4s1 | [Ar]4s2 | [Ar]4s23d1 | [Ar]4s23d2 | [Ar]4s23d3 | [Ar]4s23d4 | [Ar]4s23d5 | [Ar]4s23d6 | [Ar]4s23d7 |
| 28Ni | 29Cu | 30Zn | 31Ga | 32Ge | 33As | 34Se | 35Br | 36Kr |
| [Ar]4s23d8 | [Ar]4s23d9 | [Ar]4s23d10 | [Ar]4s23d104p1 | [Ar]4s23d104p2 | [Ar]4s23d104p3 | [Ar]4s23d104p4 | [Ar]4s23d104p5 | [Ar]4s23d104p6 |
| 37Rb | 38Sr | 39Y | 40Zr | 41Nb | 42Mo | 43Tc | 44Ru | 45Rh |
| [Kr]5s1 | [Kr]5s2 | [Kr]5s24d1 | [Kr]5s24d2 | [Kr]5s24d3 | [Kr]5s24d4 | [Kr]5s24d5 | [Kr]5s24d6 | [Kr]5s24d7 |
| 46Pd | 47Ag | 48Cd | 49In | 50Sn | 51Sb | 52Te | 53I | 54Xe |
| [Kr]5s24d8 | [Kr]5s24d9 | [Kr]5s24d10 | [Kr]5s24d105p1 | [Kr]5s24d105p2 | [Kr]5s24d105p3 | [Kr]5s24d105p4 | [Kr]5s24d105p5 | [Kr]5s24d105p6 |
On s’arrêtera là, juste après avoir indiqué l’élément suivant, le césium : [Xe]6s1.
On doit admettre que la règle de Klechkowski échoue dans quelques cas. Empirique, elle n’a pas de base théorique parfaitement sûre, et c’est là le problème. Les éléments dont la configuration est en rouge dans le tableau sont mal définis.
Pour le chrome, [Ar]4s23d4 doit être remplacé par [Ar]4s13d5. On constate qu’il s’agit simplement de déplacer un électron de l’orbitale 4s à l’orbitale 5d. Ce déplacement provient des interactions complexes entre les électrons, que la règle modélise de façon approchée.
Pour le cuivre, [Ar]4s23d9 devient [Ar]4s13d10
Le tableau précédent corrigé (pour la partie concernée) est :
| 19K | 20Ca | 21Sc | 22Ti | 23V | 24Cr | 25Mn | 26Fe | 27Co |
| [Ar]4s1 | [Ar]4s2 | [Ar]4s23d1 | [Ar]4s23d2 | [Ar]4s23d3 | [Ar]4s13d5 | [Ar]4s23d5 | [Ar]4s23d6 | [Ar]4s23d7 |
| 28Ni | 29Cu | 30Zn | 31Ga | 32Ge | 33As | 34Se | 35Br | 36Kr |
| [Ar]4s23d8 | [Ar]4s13d10 | [Ar]4s23d10 | [Ar]4s23d104p1 | [Ar]4s23d104p2 | [Ar]4s23d104p3 | [Ar]4s23d104p4 | [Ar]4s23d104p5 | [Ar]4s23d104p6 |
| 37Rb | 38Sr | 39Y | 40Zr | 41Nb | 42Mo | 43Tc | 44Ru | 45Rh |
| [Kr]5s1 | [Kr]5s2 | [Kr]5s24d1 | [Kr]5s24d2 | [Kr]5s14d4 | [Kr]5s14d5 | [Kr]5s24d5 | [Kr]5s14d7 | [Kr]5s14d8 |
| 46Pd | 47Ag | 48Cd | 49In | 50Sn | 51Sb | 52Te | 53I | 54Xe |
| [Kr]5s04d10 | [Kr]5s14d10 | [Kr]5s24d10 | [Kr]5s24d105p1 | [Kr]5s24d105p2 | [Kr]5s24d105p3 | [Kr]5s24d105p4 | [Kr]5s24d105p5 | [Kr]5s24d105p6 |
Les irrégularités sont toujours de même nature : on pourrait dire qu’elles sont régulières ! Il s’agit du transfert d’un électron, que la règle prévoirait sur l’orbitale s, vers l’orbitale d. C’est presque toujours le second électron s qui est déplacé. Mais dans le cas du palladium, ce sont les deux.
Règle de Klechkowski, règle de Hund, exceptions… On peut considérer que les configurations électroniques sont bien compliquées. Et c’est la réalité ! Les interactions entre les protons et les électrons d’un atome, qui sont tous en mouvement, constituent un problème vraiment difficile de Mécanique Quantique : c’est un problème à N corps. En fait, ce qui est surprenant, c’est au contraire qu’on puisse décrire ces configurations à l’aide de deux règles, et quelques exceptions. Leur existence montre qu’il y a, derrière toute cette difficulté, des régularités profondes dont les équations de la Mécanique Quantique tiennent compte.
On peut remarquer qu’après chaque gaz rare, on ouvre la couche suivante. Tous les éléments entre deux gaz rares ont leurs orbitales sur la couche ouverte par le premier d’entre eux ou en-dessous : du lithium au néon, la formule est [He]2s… ; du sodium à l’argon, la formule est [Ne]3s… ; du potassium au krypton, la formule est [Ar]4s… ; du rubidium au xénon, la formule est [Kr]5s… Etant donné que les lignes du tableau de Mendeleev (les périodes), construites par ressemblances chimiques, sont justement limitées par les gaz rares, on constate que l’on ouvre une nouvelle ligne du tableau à chaque fois qu’on commence le remplissage d’une nouvelle couche.
Le modèle des couches quantiques ainsi exposé permet de comprendre le tableau de Mendeleev. Mais la correspondance n’est pas simple. En particulier, les couches K, L, M… correspondent aux périodes (les lignes du tableau), jusqu’à la troisième incluse. Au-delà, nous avons vu que le remplissage se faisait en diagonale, et non plus par nombre quantique principal croissant (c’est n + l qui est croissant). Ce qui signifie qu’on laisse le remplissage de certaines sous-couches pour la période suivante.
Le tableau de Mendéléev est utilisé dans de nombreux domaines. Aussi est-il placé dans une page séparée.
Remarque La ligne 6 dont la 3e case contient une étoile), comprend 17 éléments. Si oeur ajoute les 15 éléments lanthanides (référencés par l’étoile), on obtient 32 éléments. C’est bien le nombre qu’on avait trouvé plus haut en étudiant le remplissage des orbites.
Pareillement, la ligne 7 comprend 17 éléments, et la ligne des actinides 15, donnant un total attendu de 32.
Les électrons qui entourent le noyau sont plus ou moins liés, selon leur niveau d’énergie. Ceux qui participent aux liaisons chimiques sont les moins liées. On les appelle électrons de valence. Par opposition, les autres électrons sont les électrons de cœur.
Comment les reconnaître ?
Lorsqu’une sous-couche est pleine, elle atteint une grande stabilité. Et de ce fait, les électrons qui s’y trouvent ne participent plus aux liaisons chimiques. Les électrons actifs sont ceux qui sont les plus éloignés du noyau, donc ceux qui présentent le numéro principal le plus élevé.
Les électrons de valence sont ceux dont le nombre quantique principal n est le plus élevé, ou qui appartiennent à des couches en cours de remplissage.
Les molécules sont des édifices polyatomiques. La liaison qui retient ces atomes ensemble est l’interaction électromagnétique entre les protons et électrons des atomes concernés. Les électrons qui réalisent ces liaisons sont les électrons de valence, les électrons de cœur n’interviennent pas. Les molécules obéissent elles aussi au principe d’énergie minimum habituel en physique : un ensemble d’atomes évolue vers l’état qui minimise son énergie.
Le modèle de Lewis a été proposé en 1916, avant que les principes de la Mécanique Quantique qui nous ont permi de comprendre à peu près la structure des atomes ne soient connus. Lewis a supposé que les liaisons se faisaient entre deux atomes par la mise en commun de deux électrons (éventuellement de plusieurs paires). C’est le principe d’exclusion qui justifiera a posteriori cet appariement des électrons (notez que les paires d’électrons se retrouveront bien plus tard dans l’explication de la supraconductivité ; ce sont les paires de Cooper).
Les deux électrons d’une paire peuvent provenir :
Lorsque les deux atomes mettent en commun deux paires d’électrons, on parle de liaison double ; lorsqu’ils partagent trois paires, il s’agit d’une liaison triple.
La molécule de dioxygène présente une double liaison, celle de diazote une triple liaison.
L’hélium ne possède que deux électrons, qui saturent sa couche 1s. Mais tous les autres gaz rares ont le même type de structure électronique : leur configuration électronique se termine par ns2np6, où n est leur numéro quantique principal. Ils ont donc tous leur dernière couche saturée, consituée de 4 paires d’électrons (chaque paire se trouve sur une sous-couche). Ces 4 paires forment elles-même un octet d’électrons.
La règle de l’octet stipule que les atomes, lorsqu’ils se groupent en molécules, tendent à saturer leur dernière couche non vide. Pour cela, ceux dont la structure électronique est légèrement déficitaire en électrons auront tendance à en récupérer pour la compléter ; ceux qui au contraire ont leur dernière couche presque vide, chercheront à vider cette couche, en associant les électrons en trop à leur voisin.
La règle s’énonce ainsi :
Lorsque cette configuration est atteinte, ils présentent tous deux une couche extérieure de gaz rare, forme la plus stable possible.
La représentation de Lewis est un graphisme indiquant les électrons de valence des atomes. Elle permet donc de déterminer les réactions possibles, selon que les atomes peuvent céder ou accepter des électrons.
Sans entrer dans le détail de cette représentation, indiquons seulement que la double liaison, par exemple du dioxygène, se représente avec un double trait entre les deux atomes :
Tout ce qui précède montre comment la Mécanique Quantique permet de comprendre (et de représenter assez simplement) les diverses structures des atomes. Ces structures permettent à leur tour de calculer (difficilement) les niveaux d’énergie des différents atomes, et ces niveaux d’énergie permettent à leur tour, par leurs différences, de déterminer les raies spectrales des atomes plus lourds que l’hydrogène. Mieux, le calcul permet de trouver les longueurs d’onde des raies interdites qui, comme leur nom l’indique, ne peuvent être produites au laboratoire. La spectroscopie est donc tributaire de la chimie-physique.
---=OO=---