Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Matière noire | |||||||
… dans cette grande cuisine qu’est la préparation d’un univers épicé en galaxies,
tout se joue sur la taille des grumeaux et le temps de cuisson.
Matière noire et autres cachotteries de l’Univers
Alain Bouquet, Emmanuel Monnier
Table des matières
1.1 Rapport de masse
1.2 Courbe de rotation
1.3 Forme de la courbe de rotation
1.4 L’observation initiale
1.5 L’émergence des idées
1.6 Bilan
2 Observations récentes
2.1 La radioastronomie
2.2 Le disque maximum
2.3 La loi de Tully-Fisher
2.4 Premières tentatives
2.5 Le temps des expériences
2.6 Résultat des simulations
2.7 Diversité des galaxies
2.8 Sous-structures
2.9 Stabilité des amas
2.10 CDM et la loi de Tully-Fisher
2.11 Masse manquante dans les amas
2.12 Problème cosmologique
2.13 Lentille gravitationnelle faible
2.14 Cas particulier
2.15 Chaude ou froide ?
2.16 HDM
2.17 Les neutrinos
2.18 Le modèle CDM
2.19 De quoi est faite la matière noire ?
2.20 En cas de découverte…
2.21 Une curiosité embarrassante
2.22 Explication des courbes de rotation par la matière noire
3 Modification de la dynamique
3.1 MOND
3.2 Conséquences
3.3 Loi de Tully-Fisher
3.4 Fondement de la théorie
3.5 Les courbes de rotation en détail
3.6 Les amas de galaxies
4 Bibliographie
Lorsqu’on observe une galaxie, on voit la lumière émise par ses étoiles. On peut la mesurer, et si on connait la distance de la galaxie à la Terre (par son décalage spectral par exemple), on peut déterminer sa luminosité totale (quantité d’énergie émise). Notons-là L.
On peut éventuellement déterminer la masse de la galaxie. C’est plus difficile, puisque ce n’est pas une mesure directe. Mais diverses techniques le permettent. Donneront-elles des valeurs compatibles ?
La théorie des étoiles donne une indication précieuse : elle permet d’associer une masse à un type spectral. Pour une étoile de type spectral donné (déterminé par son spectre), la masse est donc connue.
Il y a beaucoup d’étoiles plus petites que le Soleil, qui contribuent très peu à la luminosité totale, un peu plus à la masse totale. Par contre, on observe très peu d’étoiles plus grosses que le Soleil, considérablement plus lumineuses, et un peu plus massives. Connaissant la proportion d’étoiles des différents types spectraux dans la population d’une galaxie, on peut évaluer la masse totale de la galaxie. Il s’agit donc de la masse que l’on dira visible, puisqu’elle est déterminée par l’observation de la lumière des étoiles. On la note Mv.
Lorsque ces deux paramètres sont connus, on peut évaluer leur rapport Mv/L de la galaxie. Bien évidemment, Mv et L sont en unités solaires. Il y a beaucoup d’étoiles plus petites que le Soleil, mais qui contribuent peu à la luminosité totale. Par contre, on observe très peu d’étoiles plus grosses que le Soleil, mais qui sont très lumineuses. Ceci fait que le rapport Mv/L pour une galaxie typique est de l’ordre de 1.
Remarquez qu’il est calculé en utilisant le modèle astrophysique des étoiles, qui lie la masse et la luminosité de chacune.
Une courbe de rotation est un graphique montrant la vitesse orbitale d’une étoile de la galaxie, en fonction de sa distance au centre. On la mesure simplement en observant le décalage spectral de la lumière provenant des étoiles à diverses distances du centre. Ce décalage se traduit immédiatement en vitesse de rotation, et permet de tracer la courbe.
Une fois la courbe tracée, on connait les mouvements des étoiles dans la galaxie. Ces mouvements sont produits par la gravitation, un peu comme le mouvement des planètes autour du Soleil. Et comme le mouvement des planètes permet de déterminer la masse du Soleil, on peut déduire ici la masse de la galaxie. Précisément, pour une étoile orbitant à la distance r du centre, la masse attirante est celle M(r) contenue à l’intérieur de l’orbite. Pour les étoiles périphériques, cette masse est simplement celle de la galaxie, tout au moins jusqu’à la distance de ces étoiles.
Ayant déterminé la masse Md de la galaxie de cette manière (l’indice d signifie dynamique), on peut l’utiliser pour déterminer le rapport M/L. Notons Md/L sa valeur.
Nous avons donc déterminé Mv/L et Md/L. La comparaison de ces deux rapports joue un grand rôle dans les études que nous allons décrire. Naturellement, puisqu’on parle de la même quantité M/L, on doit obtenir une valeur tout à fait comparable.
La vitesse d’une étoile dépend de la masse située au-dessous de l’orbite de l’étoile dans la galaxie. Donc, plus une étoile est lointaine, plus la masse qui l’attire augmente, ce qui accroît l’attraction gravitationnelle qu’elle subit. Mais comme elle est plus loin, cette même attraction diminue comme le carré de la distance. Le résultat est assez complexe, et dépend de la répartition de la matière dans la galaxie. Le bulbe, région centrale, a une densité d’étoiles forte puis en s’éloignant, on trouve une densité d’étoiles décroissante. La masse contenue à l’intérieur de l’orbite d’une étoile est donc croissante avec la distance, mais de moins en moins. Puis on arrive aux confins de la galaxie (de la galaxie visible). Alors, la masse interne n’augmente plus, et la gravité ressentie pas les quelques étoiles lointaines ne varie plus qu’en raison inverse du carré de la distance. La vitesse orbitale de ces étoiles devrait donc diminuer comme diminue la vitesse des planètes autour du Soleil.
Par conséquent, la courbe de rotation doit montrer un accroissement de la vitesse avec la distance au centre, jusqu’à un maximum qui correspond à la région où la densité diminue, et où l’effet de la distance sur la gravité devient prépondérante. Au-delà, la vitesse de rotation doit diminuer de façon képlérienne, comme celle des planètes du Soleil.
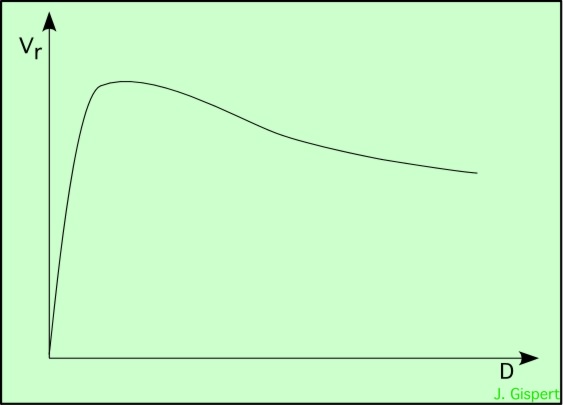
Courbe de rotation képlérienne typique
Ce schéma montre une courbe de rotation képlérienne caractéristique, avec l’augmentation rapide de la vitesse dans les régions centrales, puis un maximum, et ensuite une décroissance képlérienne lorsque la masse en-dessous n’augmente plus de manière significative.
La quête de la matière noire trouve son origine dans les observations de Zwicky (1933), qui a montré que les galaxies dans l’amas de Coma avaient une vitesse moyenne trop élevée pour rester liées. La masse visible M des galaxies (étoiles et gaz) déduite en supposant le rapport M/L = 1, est trop faible pour les retenir en orbite. Il faudrait, pour assurer la stabilité dynamique, que le rapport M/L soit de l’ordre de 500, ce que la physique des étoiles interdit formellement.
Les amas pourraient être instables par manque de masse, mais alors leur durée de vie serait brève, et on n’en observerait beaucoup moins. Ce n’est pas l’explication. Il faut donc envisager que la masse qu’on mesure par le rapport M/L n’est pas la masse totale.
Dans les galaxies, les premières observations de la vitesse des étoiles ont été difficiles, mais ont montré que le rapport M/L croît en allant du centre vers les parties externes.
En 1932, Jan Oort a observé le mouvement des étoiles de la Voie Lactée qui se trouvent en dehors du plan de la galaxie. Il a montré qu’elle étaient plus rapides que ce que la masse connue de la galaxie justifiait. Et il a parlé de matière noire pour justifier ces mouvements.
Zwicky a envisagé l’existence d’une matière noire, mais ne s’est pas prononcé sur sa nature. Il a simplement imaginé qu’elle puisse se trouver dans les galaxies, ou entre elles dans le milieu intergalactique. La matière noire dont parlent Zwicky et Oort est conventionnelle : il s’agit de particules connues, ou de poussières, de météorites, ou même d’étoiles trop faibles pour être visibles. La matière noire non baryonique n’émergera que plus tard.
En 1939, Babcock a analysé la rotation de la galaxie d’Andromède, et constaté que les vitesses ne décroissaient pas vers l’extérieur du disque lumineux. Il en a déduit que le rapport Md/L augmentait avec la distance au centre, et l’a expliqué de deux façons différentes :
Cette seconde explication, seulement envisagée, sera reprise bien plus tard…
A la fin des années 30, la première phase est terminée, le décor est en place. Deux observations ont été faites dans le visible, dans les amas de galaxies, et dans les galaxies elles-mêmes. Ces deux observations concernent des vitesses, et sont en contradiction avec la gravitation universelle. Remarquez bien que ce n’est qu’à la lumière de ce modèle théorique de la gravitation qu’un problème se pose… Dans les galaxies, le rapport Md/L croît vers l’extérieur, soit parce que Md croît, soit parce que L décroît.
Les solutions envisagées par les astronomes de l’époque se conçoivent dans ce cadre :
En 1957, Henk van de Hulst publie un article dans lequel il construit la courbe de rotation de M31 (Andromède), obtenue par l’observation des nuages d’hydrogène neutre (raie à 21 cm de longueur d’onde). Ces nuages débordent largement (35 kPc) le disque visible (moins de 20 kPc), et permettent donc de tracer la courbe de rotation bien au-delà de la dernière étoile visible. Ces observations ont largement confirmé les idées précédentes, en montrant que la vitesse orbitale reste approximativement constante au-delà du disque visible.
On peut tracer la courbe de rotation à l’aide de ces nuages, parce qu’ils ne représentent qu’une fraction peu importante de la masse de la galaxie. Ils sont donc influencés par la masse totale, sans la modifier significativement. C’est ce qui permet de les utiliser comme traceurs des vitesses.
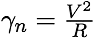
Si on se place loin du centre, en observant un nuage externe, la masse totale lui est intérieure, et l’accélération newtonienne est :
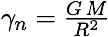
En tirant V :
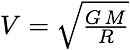
Soit V ∝ R-1/2. C’est la décroissance newtonienne des vitesses de rotation, pour les régions galactiques où la masse extérieure est négligeable.
La première observation de van de Hulst a été largement confirmée par la suite, et on considère maintenant que les courbes de rotation sont globalement plates vers l’extérieur des galaxies spirales. La vitesse de rotation est pratiquement constante, au lieu de décroître comme r-1/2.
En 1978, Albert Bosma a utilisé le radiointerféromètre de Westerbork pour déterminer les courbes de rotation externe de 25 galaxies.
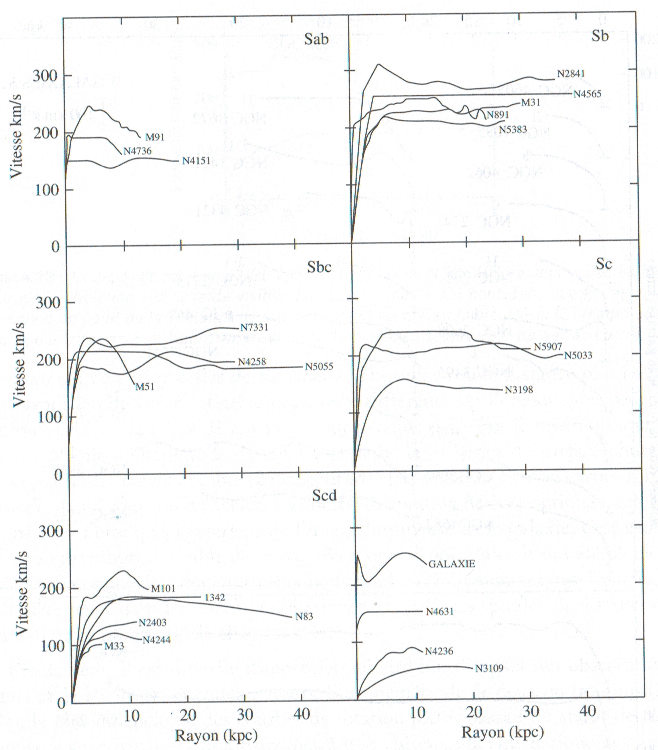
La masse intérieure à une distance r du centre croît comme M(r) ∝ r.
Des observations dans le visible ont été faites aussi, par exemple par Rudolph Kurth en 1950, qui a évalué la masse de la Voie Lactée à 3 fois la masse visible, en analysant le mouvement des amas globulaires.
Agris Kalnajs (Australie) a fait une étude poussée des courbes de rotation dans le visible, et utilisé l’approximation du disque maximum. En analysant la courbe de lumière de chaque galaxie (et non pas une courbe moyenne), et en considérant la masse maximum compatible avec la luminosité, il a trouvé que la courbe de rotation était compatible avec une rotation newtonienne… Mais le bulbe perturbait les mesures, et il a fallu le considérer à part (décomposition bulbe-disque). La conclusion de cette étude est que la partie visible de la galaxie n’est pas critique, et que la nécessité de matière noire n’est pas évidente en ne considérant que cela. C’est donc bien la rotation des nuages externes qui emporte la conviction.
En 1977, Tully et Fisher ont découvert une relation empirique entre la vitesse de rotation d’une spirale et sa luminosité. Nommée loi de Tully-Fisher, cette relation s’exprime par :
L ∝ V4
C’est une simple loi de puissance. Elle permet de déterminer la luminosité réelle d’une galaxie spirale, en mesurant sa vitesse de rotation (par spectroscopie), indépendamment de sa distance. Cette loi est l’une des mieux vérifiées dans le domaine des galaxies ; elle est valide sur une échelle de 100 en luminosité. La seule dispersion des valeurs qu’on constate est due aux erreurs de mesure.
Dès qu’on peut mesurer la vitesse de rotation d’une spirale, on en déduit sa luminosité, et par comparaison avec sa luminosité observée, on en déduit sa distance. Cette loi est donc d’une très grande utilité en cosmologie.
Mais elle présente ici un tout autre intérêt. La luminosité est proportionnelle à la masse visible de la galaxie, alors que la vitesse de rotation est fonction de la masse totale. On a donc un moyen de comparer ces deux masses.
Les observations étant à l’époque difficiles et laissant une incertitude assez importante, les astronomes ne s’en souciaient pas vraiment, et pensaient que des découvertes d’objets non lumineux résoudraient le problème. L’utilisation des satellites artificiels a permi d’observer dans l’infrarouge en particulier, et faire un bilan plus précis de la luminosité des galaxies. Les toutes petites étoiles étant de très loin les plus nombreuses, contribuent pour beaucoup à la luminosité, mais dans le rouge et l’infrarouge. Aussi étaient-elles plutôt oubliées avant l’ère spatiale.
Tous les objets visibles ne résolvant pas le problème, il fallait en chercher d’autres. On a recherché :
Les objets compacts de ce genre (naines brunes, naines blanches, trous noirs…) ont été nommés collectivement MACHOs (Massive Compact Halo Objets). Leur recherche a été faite par des moyens systématiques puissants : projet européen EROS (Expérience pour la Recherche d’Objets Sombres), projet américain MACHO, qui ont suivi les effets de lentille gravitationnelle sur quelques millions d’étoiles, puis AGAPE (Andromeda Galaxy Amplified Pixel Experiment) qui en a suivi 10 milliards. Leurs résultats ont montré que très peu de tels objets peuplent le halo de la Voie Lactée et d’Andromède.
La prise en compte de tous ces objets a un peu amélioré la situation, mais pas assez pour résoudre le problème. Cette matière-là ne suffisant pas, qu’imaginer d’autre ?
Arrigo Finzi a explicitement envisagé une modification de la loi de la gravité, qu’il voyait plutôt en 1/r1,5 qu’en 1/r2. Mais en 1963, c’était difficile de toucher à la Gravitation Universelle, qui a été étendue par la relativité générale. Même aujourd’hui…
La matière noire et d’un type totalement inconnu. Comment l’étudier ? Tout d’abord, en essayant de cerner ses propriétés. Où est-elle ? Comment se comporte-t-elle ?
Puisque tout ce que nous savons d’elle est son activité gravitationnelle, c’est bien par là qu’il faut commencer. Il faut essayer de savoir où elle est, comment elle est répartie, et en quoi elle résoud les problèmes dynamiques correspondants.
Les questions de dynamique galactique sont :
La puissance de calcul des ordinateurs permet de décrire des points matériels dans l’espace, représentant les étoiles d’une galaxie, et de calculer comment ils s’attirent gravitationnellement. On peut alors déterminer où ils seront un instant après. Puis là, recalculer les forces, et ainsi de suite… Au bout d’un certain temps de calcul, on arrivera à faire tourner une galaxie sur elle-même.
Lorsque de telles simulations ont été réalisées pour la première fois, la puissance de calcul limitait beaucoup le nombre d’étoiles qu’on pouvait décrire. Cependant, on est arrivé à une conclusion concernant la dynamique des galaxies :
Dans les spirales, les orbites des étoiles sont pratiquement circulaires et dans un même plan, ce qui donne à l’ensemble une dynamique de rotation. Dans les elliptiques, les orbites sont très elliptiques, et orientées au hasard. Par analogie avec les molécules d’un gaz, on peut considérer que les galaxies elliptiques sont chaudes (en ce sens que les vitesses des étoiles y sont élevées).
Analysons plus finement les premiers résultats. Une galaxie contient des étoiles et du gaz, et l’on doit modéliser les deux. Mais leur comportement est différent. Les étoiles sont des objets condensés, le gaz est diffus. Dans leurs relations, les étoiles s’ignorent presque totalement les unes les autres, parce que leurs distances sont considérables. Dans une galaxie spirale aux orbites régulières, il n’y a pratiquement pas d’influence des étoiles entre elles, sauf par leur masse globale, cumulée. Par contre, un atome de gaz apprtenant à un nuage a toutes chances de heurter prochainement un autre atome d’un autre nuage. Par rapport à leur section efficace (leur champ d’action), leurs distances sont faibles. Aussi, les atomes du gaz perdent-ils en permanence de l’énergie, ce qui a pour effet de les refroidir. Alors, les chercheurs ont aménagé leur simulation pour refroidir le gaz. Et là, la structure spirale s’est particulièrement bien manifestée.
La galaxie simulée est divisée en deux composantes :
On doit se souvenir ici que les magnifiques bras spiraux des galaxies sont des ondes de densités, des régions où la matière est plus condensée et forme des étoiles. L’aspect brillant des bras vient de la forte luminosité des étoiles massives ainsi formées, dont la durée de vie est faible. Quand elles s’éteignent, l’onde de densité est allé un peu plus loin, et a allumé d’autres étoiles, qui tracent ainsi visuellement la rotation du bras.
Mais les étoiles laissées derrière les bras peuplent la totalité du disque, leur densité est uniforme. Etoiles et gaz n’ont donc pas le même comportement, et l’artifice du refroidissement du gaz dans les simulations a bien mis en évidence ce phénomène.
Les simulations sont donc un outil très efficace, permettant de jouer avec des paramètres, afin de voir quels sont ceux qui permettent de modéliser au mieux ce que l’on observe.
Il ne reste donc plus qu’à y ajouter la matière noire, pour essayer d’obtenir des courbes de rotation réalistes. La répartition qui donnera ces courbes devrait être pertinente.
Avant d’incorporer cette matière noire dans les simulations, on doit se demander ce qu’il faut modéliser. La matière noire agit gravitationnellement, mais elle est invisible : elle ne brille pas, elle n’absorbe pas la lumière non plus. On n’observe pas plus de désintégrations, qui donneraient des photons, ou d’autres particules observables. La seule chose à mettre dans les simulations est donc la masse de cette matière, avec bien sûr une répartition appropriée.
Les galaxies sont construites régulières, isotropes. Rapidement, une structure spirale apparaît, avec une barre centrale. Mais elle disparaît tout aussi vite au profit d’une structure chaude : les orbites deviennent fortement elliptiques, et les interactions entre les étoiles fréquentes. Spontanément, la galaxie est passé d’un équilibre de rotation à un équilibre de pression.
Pour éviter cette dissipation de la structure, qui n’est pas observée, Ostriker et Peebles ont modélisé un halo de matière noire entourant une galaxie spirale. Cette matière est chaude (la vitesse des particules est importante), et sa masse est au moins égale à celle de la masse visible. Avec ces ingrédients, ils ont obtenu des galaxies simulées qui ressemblent fort aux galaxies réelles. Le point le plus important est que ce halo stabilise la structure spirale.
Un tel halo n’est pas tout à fait nouveau. Les amas globulaires et quelques étoiles en constituent un, bien visible, autour des spirales. Il suffit donc d’imaginer qu’il contienne, en plus, de la matière exotique.
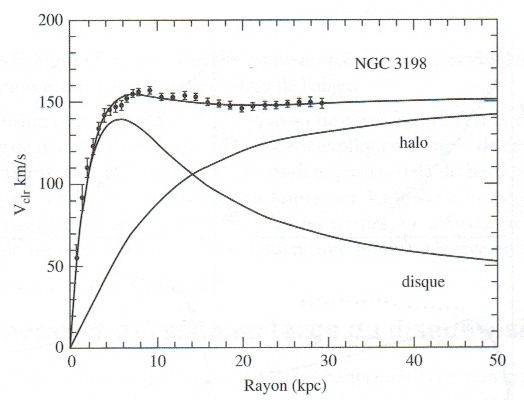
Il y a une différence, notée dans les années 90, entre les galaxies spirales à forte brillance superficielles (HSB pour High Surface Brightness ≈ 100 L /pc2), et les autres (LSB pour Low Surface Brightness ≈ 10 L /pc2). Les HSB montrent une courbe de rotation quasiment newtonienne, alors que les LSB s’en écartent beaucoup. Les courbes de rotation optiques ne sont pas vraiment probantes pour affirmer l’existence de la matière noire. Il faut invoquer les courbes étendues aux nuages de gaz externes.
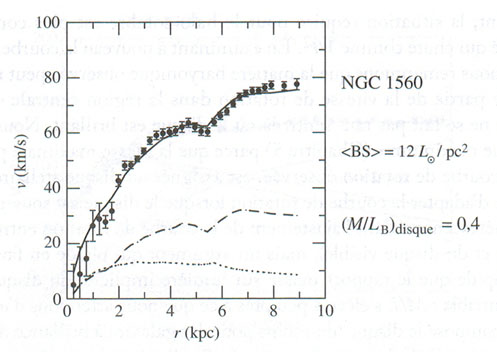 |
 |
Clairement, ce schéma nous montre que les galaxies à faible brillance de surface (à gauche) ont une courbe de rotation qui monte doucement, alors que les autres montent brusquement et passent par un maximum. Les galaxies à faible brillance superficielle sont faibles, et dificiles à voir. Aussi n’ont-elles été étudiées que récemment. Ces petites galaxies sont totalement dominées par la matière noire, la matière normale qui les constitue est négligeable. Leurs courbes de rotation sont difficiles à expliquer par le modèle du halo CDM. Pour sauver le modèle, on peut faire intervenir l’évolution de la galaxie, avec des mouvements de matière normale (explosions de supernovæ) qui, par leur action gravitationnelle, pourraient avoir modifié la répartition de la matière noire.
Les simulations d’évoution pour ces halos de matière noire montrent une fragmentation. Le halo principal baigne une grande quantité de petites condensations, plusieurs centaines. C’est une conséquence de la formation hiérarchique des halos, par condensation de petits objets, qui se regroupent pour en former de plus gros. Le halo de la galaxie est donc le résultat de ces fusions. Mais on s’aperçoit que la fusion est imparfaite, les petites structures ne se laissant pas déchiqueter par les grosses. Elles subsistent donc.
Autour de la Voie Lactée, on observe effectivement des sous-structures : ce sont les galaxies naines sphéroïdales. Mais on n’en connait qu’une douzaine, ce qui est bien insuffisant. Il reste la possibilité que des sous-halos de matière noire existent, sans matière normale suffisante pour être visible…
En fait, la solution proposée pour résoudre un problème en pose d’autres !
Ce qui explique la stabilité des galaxies peut aussi expliquer celle des amas. Des simulations à cette autre échelle ont été faites. Elles indiquent qu’il faudrait beaucoup de matière noire pour expliquer cela, en fait une bonne centaine de fois la masse visible. C’est en accord avec les observations initiales de Zwicky, et de nombreuses autres, plus récentes.
Si l’hypothèse de départ (il y a de la masse invisible, et la gravitation newtonienne est correcte), alors cette masse est largement dominante par rapport à la masse visible. Ce qui constitue une toute autre vision de l’Univers…
De plus, pour expliquer la vitesse de rapprochement de la galaxie d’Andromède, les masses d’Andromède et de la Voie Lactée sont bien insuffisantes. Là encore, de la matière noire est bienvenue pour améliorer la situation.
Enfin, dans les amas comme Coma, on a refait des mesures de vitesse et montré que la masse visible est bien insuffisante, confirmant les premières constatations de Zwicky.
Remarquez que les simulations ne présagent pas de la nature de la matière qu’il faut ajouter pour stabiliser. Elle peut être normale et non détectée, aussi bien qu’exotique. De la matière normale a bien été détectée etre les galaxies dans les amas, sous la forme de grands nuages d’hydrogène chaud (quelques millions de degrés) imaginés initialement par Finzi. Mais ils sont loin d’atteindre la masse nécessaire.
Tout ce faisceau de faits observationnels, et de simulations, a donné sa force au concept tout théorique de matière noire. Il ne reste plus qu’à l’observer…
Le paradigme CDM doit aussi expliquer la loi de Tully-Fisher, qui est empirique. Les observations récentes en ont fixé l’exposant à 4.
Analysons cette loi. Elle dit que L ∝ V4. L est la luminosité globale de la galaxie dans le proche ifrarouge. Elle reflète directement la masse baryonique des étoiles. De l’autre côté, V est la vitesse marginale de la spirale, elle est définie par la masse totale de la galaxie, donc fortement liée à la matière noire. L’équation de Tully-Fisher met donc en regard la matière ordinaire à gauche, et la matière noire à droite. Comment peut-on expliquer un tel lien, ces deux formes de matière interférant si peu ? Puisqu’i n’y a pas d’interactions, ce lien ne peut être acquis, il devrait alors être produit par la formation des spirales.
Après le découplage de la matière noire, vers z = 100.000, les fluctuations de matière noire ont pu commencer à s’effondrer, et à cosntituer des structures. Ces objets ont donc une origine très semblable, et sont autogravitants, comme les nébuleuses habituelles. De ce fait, leur masse M est proportionnelle au cube de leur rayon R3 : M ∝ R3. Puisqu’ils sont en équilibre, ils doivent, comme la matière ordinaire, satisfaire au théorème du viriel (partage entre l’énergie cinétique et l’énergie potentielle), et donc V2 = G M / R. De ces deux relations, il est immédiat de tirer : M ∝ V3. Les simulations montrent en effet une telle relation, mais avec une grande dispertion des valeurs (la proportionnalité n’est qu’approximative). Mais remarquez que cette relation ne fait intervenir que la matière noire, et non la matière ordianaire comme la loi de Tully-Fisher.
Alors, pour passer de l’une à l’autre, il faut faire intervenir la façon dont la matière ordianire, après son propre découplage vers z = 1.000, va à sont tour s’effondrer. A ce moment-là, les halos sombres sont déjà structurés, et par leur gravité vont guider la matière habituelle. La matière va donc se condenser vers le centre du halo sombre, mais cette condensation s’arrêterra lorsque la rotation produira assez de force centrifuge pour cela (moment cinétique suffisant). Si on admet que la vitesse de rotation di disque baryonique est est proprotionnelle à la dispersion des vitesses de la matière noire dans le halo, alors on arrive à une relation de la forme Tully-Fisher, mais avec un exposant 3 et non 4 : L ∝ V3.
Pour sauver la matière noire, on peut invoquer que le scénario de formation des galaxies est loin d’être maîtrisé à l’heure actuelle, et que dans ces incertitudes on trouvera le moyen d’augmenter l’exposant… C’est tout à fait possible, mais cette discordance entre la loi prévue et la véritables loi observée est tout de même un gros éceuil pour le paradigme CDM.
Faber et Gallagher en 1979 ont obtenu un rapport M/L ≈ 100. Les amas comme Coma ont une masse visible de l’ordre de Mv ≈ 1013 L, alors que leur masse dynamique Md ≈ 1015 L. Ces données confirment celles obtenues bien plus tôt par Zwicky.
La plupart des galaxies des amas sont elliptiques, sans rotation d’ensemble et dépourvues de gaz. Si M/L ≈ 100 pour l’amas, en supposant que la matière noire soit associée aux glaxies et non diffuse, chaque galaxie doit avoir aussi un rapport M/L ≈ 100. Donc les grandes elliptiques auraient une grande masse, et elles devraient tomber vers le centre de l’amas. Ce qui n’est pas le cas. Donc, le gaz doit être diffus, au moins partiellement.
Depuis les années 70, on utilise des télescopes spatiaux à rayons X. Et ils ont découvert du gaz chaud dans les amas. La température est de l’ordre de 107 K et correspond à une vitesse des atomes de 1.000 km/s. Finzi avait justement prévu l’existence d’un gaz dont les atomes auraient la même vitesse que les galaxies, ce qui est le cas. Finzi avait compris aussi que sa densité devait être faible, sans quoi il se serait déjà refroidi. C’est bien ce qui a été observé, même si la densité est assez élevée dans certains amas pour que le refroidissement ait déjà commencé. Mais même dans ce cas, la masse est trop faible pour satisfaire l’équilibre.
Le satellite à rayons X Eisntein en 1978 a cartographié la répartition de ce gaz dans les amas.
Dans les amas denses, la masse de ce gaz atteint 1013, 1014 M, soit 3 à 4 fois la masse des étoiles. Le gaz invisible (en optique) domine donc largement la matière visible condensée en étoiles. On a donc découvert une partie de la matière noire…
La masse dynamique de l’amas est de ≈ 1015 M. Le rapport (M* + Mgaz) / Md reste de l’ordre de 5 ou 6. Il manque encore beaucoup de matière pour assurer la stabilité dynamique des amas…
Pour produire les éléments chimiques après le Big Bang, il faut que la densité baryonique (la matière ordinaire) soit de Ωb = 0,04 (4 % de tout ce qu’il y a dans l’Univers). S’il y a 6 fois plus de matière noire, cela fait ΩMN = 0,24. Matière ordinaire et matière noire constituent donc Ωmatière = Ωb + ΩMN ≈ 0,3.
Les observations les plus récentes montrent que l’Univers est plat, à courbure nulle globalement, c’est-à-dire euclidien. Dans ces conditions, sa densité doit être égale à la densité critique, par définition de celle-ci (les Ω sont le rapport d’une densité à la densité critique), donc Ωtot = 1. Par conséquent, il nous manque encore 70 % de l’Univers…
Le phénomène de lentille gravitationnelle a été imaginé à la suite de la publication de la Relativié Générale. Il a été plus tard observé sous la forme d’arc lumineux, qui sont des images de galaxies lointaines, ou de quasars, déviées et déformées par la masse d’un amas situé entre l’objet et nous. Ces observations sont une validation de la relativité générale.
Puisque cette théorie est confortée, on peut rechercher des effet de lentille gravitationnelle faible, produits par des objets de masse plus petite. On n’attend pas d’arcs somptueux, mais plus prosaïquement des déformations des galaxies proches. Celle-ci doivent perdre leur forme approximativement circulaire, et s’allonger dans les sens de la gravitation. On peut objecter (et on le fait) que les galaxies ne sont pas rondes, mais elliptiques. Cependant, l’orientation d’une galaxie donnée par rapport à la Terre est tout à fait aléatoire. Dans un champ, les galaxies visibles sont orientées au hasard. Alors, si on observe un allongement systématique de toutes ces galaxies vers un point particulier, on peut considérer que c’est une déformation gravitationnelle orchestrée par une masse occupant ce point. Ce phénomène permet, avec toutes les difficultés observationnelles qui l’accompagnent, de cartographier le ciel et de déterminer le masses perturbatrices.
Remarquez que cette méthode pour peser les galaxies ne s’appuie que sur la relativité générale, alors que la méthode par les rayons X nécessite d’assumer l’équilibre hydrostatique. Ce dernier a des chances d’être réel, mais peut-être pas dans tous les cas.
Les masses obtenues par cette méthode sont en très bon accord avec celles déterminées par les rayons X.
Il existe un amas de galaxies, découvert en 2006, qui est tout à fait particulier. Il se nomme amas du Boulet, et se trouve à z = 0,296 ou encore 2.500 Mpc (avec H0 = 74 km/s/Mpc). Cet amas est tout à fait étonnant. C’est en fait un amas double, avec une composante mineure éloignée de 720 kpc. Chandra, en rayons X, a trouvé deux grands nuages de gaz, associés aux deux amas, mais pas centré sur les étoiles ; ils sont entre les amas. L’un des deux nuages montre de manière évidente les traces d’un choc supersonique avec un autre nuage. En fait, l’explication est simple (en apparence) : les deux amas sont entrés an collision, les systèmes de galaxies se sont croisés sans interactions, mais les nuages de gaz ont subi un choc. La perte d’énergie du gaz lors du choc les a dissociés des galaxies, et ils sont maintenant en arrière d’elles.
Mais la surprise vient de l’analyse par lentille gravitationnelle. La distortion des images des galaxies du champ indique où se trouve la masse qui la produit. Et celle-ci correspond aux galaxies, et non au gaz. Alors ? Si on imagine que la matière noire se comporte un peu comme du gaz, elle aurait dû subir le choc, et traîner comme les nuages. Sa masse se manifesterait ainsi dans le nuages de gaz, et non dans les systèmes stellaires. Il fait admettre que cette matière noire n’a pas subi le choc… Elle est sans dissipation. Les particules de matière noire n’interagissent pas lorsqu’elles se croisent ! Curieux comportement. En particulier, il indique que cette matière n’est pas baryonique, ce dont on se doutait.
La matière est chaude lorsque les particules qui la composent se déplacent à grande vitesse. On peut donc imaginer que la matière noire soit froide ou chaude, selon la vitesse de ses particules. Aux premiers instants de l’Univers, tout était en équilibre thermique. Il est facile de l’imaginer : la densité était telle que toutes les particules, quelle que soit leur section efficace, se heurtaient. Et par là, équilibraient leur température. Mais lorsque la densité, en baissant, passait en-dessous d’un certain seuil, la section efficace d’un type de particule se trouvait trop petite pour que la particule interagisse encore. On parle de découplage. Ce type de particule continue donc son existence indépendante, sans plus interagir avec les autres.
La matière noire, selon ses propriétés, pourrait être aujourd’hui chaude ou froide. On a donc exploré les deux possibilités. La version chaude est nommée HDM (Hot Dark Matter en bon français), et la froide naturellement CDM (Cold Dark Matter).
Considérons d’abord le cas HDM. Il concerne de la matière qui, au moment de son découplge du reste de l’Univers, se déplace à une vitesse fortement relativiste, donc très proche de la vitesse de la lumière. Auparavant, elle était donc en équilibre thermique avec l’Univers. La matière noire naturelle qu’on a considéré était les neutrinos. Ces particules ont beaucoup de caractéristiques adéquates, la seule donnée qu’il manquait au tableau pour conclure était leur masse.
Leur masse était bornée supérieurement : on savait qu’elle était inférieure à une dizaine d’eV, alors que l’électron, bien léger, a une masse de 511 keV. Cette masse était donc si petite, que les physiciens ont pris l’habitude de la considérer nulle, possibilité tout à fait raisonnable. Mais la physique du Soleil en a décidé autrement. Lorsqu’on a enfin construit des détecteurs à neutrinos (qui interagissent si peu avec la matière que c’est bien difficile), on a constaté un déficit significatif dans les neutrinos solaires. Il fallait remmettre quelque chose en cause, soit la physique du Soleil, soit celle des neutrinos. Le modèle du Soleil étant par ailleurs très bien adapté, c’est la masse du neutrino qui a été mise en question.
Si cette masse est nulle, le neutrino ne peut pas se désintégrer. Or les expériences détectaient le neutrino électronique seulement, ignorant les neutrinos muonique et tauique. Imaginant que le neutrino électronique puisse se désintégrer dans l’un des deux autres types, il serait normal d’en observer sur Terre moins que ce que le Soleil en produit. Le modèle du Soleil serait sauf. C’est ce qui s’est passé.
Les physiciens ont fait des expériences bien contrôlées, entre le CERN à Genève producteur de neutrinos, et le Gran Sasso près de Rome, détecteur. Et le déficit observé a montré que le neutrino se désintègre bel et bien, donc qu’il a une masse.
Par conséquent, le neutrino pourrait être la particule de matière noire recherchée. Mais pour cela, il faudrait que sa masse atteigne quelques 20 ou 30 eV, il est donc disqualifié. Il joue certainement un rôle, mais secondaire.
La matière est regroupée en galaxies, amas et superamas. Comment ces structures se sont-elles formées ? Il y a deux scénarios possibles, soit elles se forment par regroupement, les petites en premier, qui fusionnent progressivement pour obtenir les grosses, soit par éclatement, les grosses d’abord, qui se fragmentent pour donner les petites.
Que s’est-il passé, dans un Univers baigné de matière noire chaude ? Les neutrinos se sont découplés lorsque leur énergie est tombé à 2 MeV environ. Etant donné leur masse dérisoire, ils étaient hautement relativistes. Dans ces conditions, ils constituent un bain si chaud, qu’ils effacent toutes les fluctuations de densité qui pourraient se former. Ceci pour des échelles de la taille de l’Univers… tel qu’il était. Mais à cette époque, il était bien plus condensé qu’aujourd’hui. Pour une masse de 17,5 eV, les neutrinos se découplent à z = 105, soit 700 ans après le Big Bang, et l’horizon de l’Univers n’était que de 700 AL. Aujourd’hui, à z = 0, cette partie de l’Univers atteint la dimension de 700 105 AL = 70 millions d’AL ou 20 Mpc. Ce qui veut dire que notre fluctuation de 700 AL à l’époque était détruite, et donc les amas de galaxie n’existent pas (aujourd’hui) !
Les galaxies ne peuvent donc se former que beaucoup plus tard, lorsque l’horizon aura bien augmenté. Les simulations numériques montrent que ceci se réalise à z = 2. Or on observe des galaxies à des décalages bien supérieurs, bien plus anciennes.
Un autre argument est bien plus subtil. Il s’agit du théorème de Liouville, qui précise que les particules ultra-relativistes ne peuvent jamais dépasser l’énergie qu’elles avaient un moment du découplage. Ceci se traduit par le fait qu’elles ne peuvent pas peupler davantage l’espace des phases, et ressemble un peu au principe d’exclusion de Pauli. Cet argument disqualifie la matière noire chaude.
L’impossibilité de former les petites structures au bon moment, met à mal le modèle de matière noire chaude. On montre que cette difficulté est la même que pour les autres particules envisageables. On a donc abandonné le modèle HDM.
Examinons maintenant le modèle CDM. La matière noire froide est non-relativiste, c’est-à-dire qu’au moment de son découplage, la vitesse moyenne des particules est bien en-dessous de celle de la lumière. Une particule dont la masse serait de 100 GeV, et qui se découplerait à une température de 10 GeV, ne pourrait pas se déplacer à une vitesse relativiste. Ce serait de la matière noire froide.
La matière noire froide ne transmet pas les informations comme la chaude, sa vitesse étant bien faible. Aussi, les fluctuations de densité ne sont pas effacées par elle, et l’argument de formation des galaxies tombe naturellement. La CDM est un candidat, de ce point de vue, tout à fait présentable.
Dans ce modèle, nous avons deux composantes de l’Univers : la matière baryonique normale, et la matière noire. A cela s’ajoutent les photons et les neutrinos. Au début, tout cela est en équilibre. Puis la matière noire se découple du reste à z = 100.000, et enfin, à z = 1.000, les photons se découplent de la matière ordinaire. Entre z = 100.000 et z = 1.000, la matière noire n’est plus perturbée, et ses fluctuations peuvent parfaitement s’amplifier. Lorsque z tombe à 1.000, la matière ordinaire à son tour peut vivre sa vie. Mais elle est libérée à un moment où la matière noire a déjà formé des embryons de structure. Et sa gravitation attire la matière ordinaire, qui se précipite dans ces puits de potentiel.
Dans ce modèle, les petites galaxies se forment très tôt, et se regroupent progressivement pour constituer des galaxies plus grosses, des amas et des super-amas.
Ceci a une influence sur la taille des structures produites.
C’est là tout le problème. On n’en sait rigoureusement rien… Mais on imagine ce qu’elle doit être :
Pour ces raisons, on appelle ces particules hypothétiques WIMPs (Weakly Interactive Massive Particles). Wimp signifie mauviette en anglais. Ainsi, pour expliquer les anomalies gravitationnelles dans le cosmos, on invoque des machos et des mauviettes…
Le modèle standard de la physique des particules nous propose les leptons (électron, muon, tau, et neutrinos associés), et les baryons (proton, neutron, constitués de quarks) ; à cela s’ajoutent les particules d’interaction, ou fermions : photon, bosons faibles W+, W- et Z0, gluons, et graviton (ce dernier n’ayant jamais été observé). Les baryons constituent donc la matière baryonique, celle que nous connaissons. Les particules hypothétiques ne faisant pas partie de cette liste constituent la matière non baryonique, jamais détectée à ce jour.
Une première hypothèse, concernant la matière noire, a été de la rechercher dans la liste connue. Seuls les neutrinos, dont on a parlé plus haut, étaient candidats. Mais on sait maintenant qu’elle est très faible, de l’ordre de 1 eV, et donc bien insuffisante.
Force est donc de rechercher des particules exotiques. Mais pour cela, les physiciens s’appuient sur des théories connues, qui pourraient être vérifiées bien qu’elles ne le soient pas encore. La première est la supersymétrie (SUSY). Elle prévoit un échange entre bosons et fermions. Dans la physique standard, il y a une barrière entre les deux classes. On envisage de la lever…
La supersymétrie oblige à doubler le nombre des particules, car les particules connues ne sont pas supersymétriques les unes des autres. Et parmi les nouvelles, il doit y en avoir une plus légère que les autres. Elle ne peut donc pas se désintégrer. Cette particule aurait-elle les bonnes propriétés pour être la matière noire ? Il faudrait déjà qu’elle existe, ce qui n’est pas prouvé.
D’autres théories physiques spéculatives ont été envisagées, apportant des particules nouvelles. Mais rien à ce jour n’est venu étayer ces théories.
La découverte éventuelle d’une particule nouvelle se ferait dans le LHC, le plus grand accélérateur de particules d’aujourd’hui. Les collisions entre particules existantes se feront à une énergie de 14 TeV à son redémarrage prochain. Ce qui veut dire que des particules de grande masse pourront être produites à partir de cette énergie. Comment découvre-t-on une nouvelle particule ? De façon indirecte et statistique. En fait, on ne la "voit" pas. On trace des courbes, obtenues à partir d’une très grand nombre d’expériences (??). Et parfois, dans une de ces courbes, apparaît une bosse, qui montre que là, quelque chose se passe. "Là" signifie à cette énergie, donc à cette masse précise. La courbe est obtenue comme moyenne des résultats d’une grand nombre de collisions. Elle a donc une valeur statistique. Elle montre qu’il existe quelque chose, mais ne dit rien des propriétés de la chose. Le boson de Higgs a été découvert ainsi, et ses propriétés ne sont pas encore conuues.
Alors, imaginant qu’on découvre ainsi une nouvelle particule, supersymétrique ou non, il faudra faire encore de nombreuses expériences pour arriver à en déterminer les propriétés. Et rien ne dit que ces propriétés cadreront avec celles attendues de la matière noire. Autrement, dit, il est tout à fait envisageable de découvrir une particule qui ne soit pas de la matière noire ! A contrario, si le paradigme de la matière noire est exact, il faudra bien qu’un jour ou l’autre on la découvre. Mais il faut bien voir que si la matière noire n’existe pas, on ne pourra jamais l’affirmer ! On pourra toujours imaginer que quelque chose nous échappe encore… L’un des problèmes de fond de cette théorie est justement qu’elle n’est pas réfutable.
On a observé la collision récente de deux amas de galaxies, dans plusieurs domaines de longeurs d’onde, et l’interprétation est difficile.

L’amas du boulet 1E0657-56, photo satellite Chandra NASA
Les deux amas s’éloignent l’un de l’autre. Cette photo est composite, et regroupe :
On voit bien que la masse est centrée sur les galaxies. Mais les nuages chauds sont restés en arrière… Lors d’une collision de galaxies, ou d’amas de galaxies, les étoiles ou les galaxies se croisent sans se heurter, car leurs distances sont bien grandes devant leurs dimensions. Par contre, les nuages de gaz qui les accompagnent se heurtent violemment, et sont freinés par le choc. Le nuage de droite a d’ailleurs une forme caractéristique produite par une onde de choc supersonique. Il est donc tout à fait normal de voir les nuages de gaz désolidarisés des galaxies et à la traîne. On dit qu’il y a dissipation d’énergie pour le gaz, mais pas pour les galaxies.
Par contre, la masse se trouve bien centrée sur les galaxies visibles. Ce qui veut dire que la matière noire, qui confère cette masse aux amas, a traversé la collision sans dissipation, comme (noire essentiellement, puisque la matière normale est rare à l’extérieur) est le rapport de la masse au volume V. Donc ρ ∝ M(r) / V. Mais celui-ci varie comme r3. Donc ρ ∝ M(r) / r3. Et puisque M(r) est proportionnel à r : ρ ∝ r / r3 = les galaxies. S’il s’agit de particules, celles-ci ne subissent pas de dissipation, ce qui n’est pas le cas de la matière ordinaire ! Cette observation plaide donc vraiment en faveur de la matière noire exotique.
Nous avons vu plus haut que, à l’extérieur des spirales, là où la luminosité disparaît, la courbe de rotation est plate au lieu de décroître. Et la formule qui donne la vitesse de rotation à la distance r est telle que :
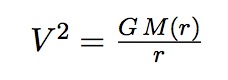
Si la vitesse doit être constante, alors le membre droit de cette formule l’est aussi. G étant une constante, il faut de M(r) / r le soit également. Par conséquent, M(r) ∝ r. Mais la densité de matière1 / r2.
Ainsi, pour justifier des courbes de rotation plates, la matière noire doit se répartir de façon très précise, et augmenter se densité graduellement tandis que celle de la matière normale diminue… Le lien entre les deux est si fort, que l’on parle de conspiration disque-halo. C’est assez troublant de voir une telle entente entre deux formes de matière qui, par ailleurs, semblent s’ignorer superbement !
On doit remarquer aussi que la vitesse constante due au halo n’a a priori aucune raison d’être égale à la vitesse maximum donnée par la matière visible. Ceci aussi montre la conspiration.
Prenons le problème à l’envers. Imaginez-vous frabriquer une galaxie spirale. Mettez de la matière normale, visible, en la répartissant pour donner l’aspect visuel habituel d’une spirale. Maintenant, ajoutez de la matière noire. Quelle quantité ? Puisque les deux types de matière sont indépendantes, vous pouvez mettre la quantité que vous voulez ! Croyez-vous que vous obtiendrez une courbe de rotation plate ? Il y a peu de chances… Pire, rien ne vous empêche de faire varier, d’une galaxie à l’autre, à la fois la quantité de matière noire et sa répartition. Et d’obtenir des courbes de rotation de formes diverses, différentes d’une galaxie à l’autre.
Cette petite expérience de pensée nous montre l’importance de la répartition précise de la matière noire par rapport à la matière normale, alors qu’elles sont indépendantes l’une de l’autre… Pour que la matière noire soit la solution au problème des courbes de rotation, il faut donc lui reconnaître des propriétés bien étranges : indépendante de la matière normale, mais variant en parfaite harmonie avec elle.
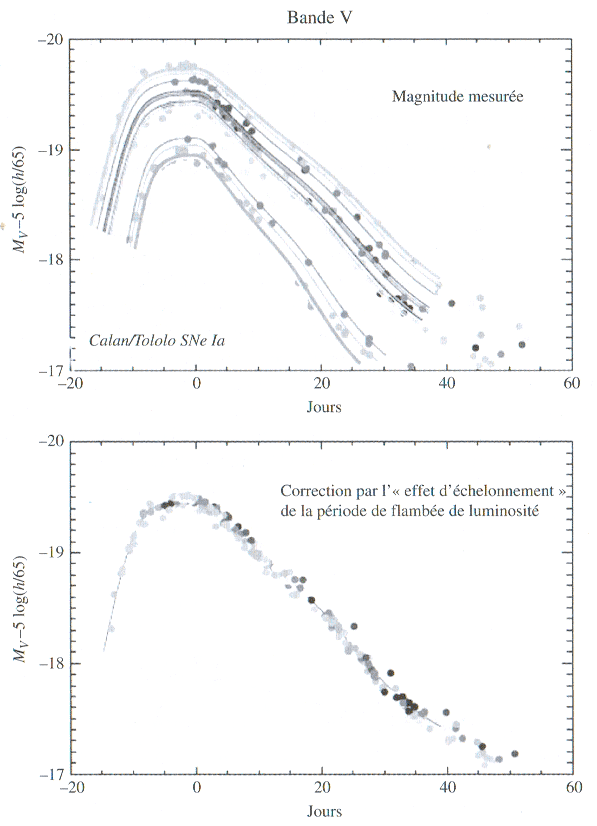
Le problème provient de la discordance entre les mouvements observés et les mouvements prévus. Ceux-ci sont calculés à partir de la matière visible, en utilisant la loi de Newton (ou la Relativité Générale, ce qui revient au même, sauf en cosmologie). Par conséquent, une hypothèse (au moins) est fausse. Soit la masse observée est trop faible (d’où le paradigme de la matière noire), soit la gravité est mal comprise, soit ce sont les deux qui sont à remettre en cause ! C’est le deuxième point qu’on va maintenant aborder.
MOND (MOdified Newtonian Dynamics) a été proposée par Mordehai Milgrom, astrophysicien israélien. Il a réfléchi sur la façon de modifier la loi de newton pour obtenir une théorie qui satisfasse les observations.
La dynamique est définie par deux lois : la force agissante, et la réaction des corps à cette force. La première est la loi de la Gravitation Universelle F = G M m / r2. La seconde est la loi de l’inertie, découverte par Galilée, et que Newton a écrite F = m γ. Milgrom a vite abandonné la modification de la gravitation elle-même, pour jouer sur la loi de l’inertie.
Newton a obtenu ses deux lois à partir des lois de Képler, qui régissent le mouvement des planètes autour du Soleil. Pour préciser, ces lois ont été établies à partir du mouvement de la seule planète Mars, dont Képler avait des positions précises sur une longue durée. Ensuite, elles ont été extrapolées avec succès aux autres planètes. Puis les lois de Newton ont été largement validées dans le domaine du système solaire, domaine défini par un certain niveau de forces, et des distances qui s’expriment en millions ou milliards de kilomètres.
Lorsqu’on explore les confins des galaxies spirales, la valeur de la force de gravitation qu’on y rencontre est bien plus faible que dans le système solaire, et les distances sont bien plus grandes. On est donc bien dans un cas où les lois de Newton sont largement extrapolées pour leur faire dire quelque chose pour quoi elles n’ont été faites. Est-ce raisonnable ?
Milgrom est parti de la loi de Newton, réécrite sous la forme :
F = m γ = m γ2 / γ
Maintenant, on remplace le γ du dénominateur par une constante γ0.
F = m γ2 / γ0.
Bien sûr, ceci modifie la loi, puisque la simplification ne peut plus se faire. Aussi réserve-t-on cette forme modifiée au domaine où les accélérations sont très faibles (par exemple au large des spirales). On a donc maintenant deux formes différentes de la loi fondamentale de la dynamique. Elles s’appliquent dans deux domaines différents :
| lorsque γ ≫ γ0 | F = m γ | |
| lorsque γ ≪ γ0 | F = m γ2 / γ0 | |
| entre les deux | non défini |
Le fait que la fonction ne soit pas définie entre ces deux domaines n’est pas critique. C’est forcément une fonction qui permet de passer en douceur d’un domaine à l’autre. Et le but de cette théorie est de montrer une alternative dans le domaine des petites gravités. Elle sera à améliorer par la suite.
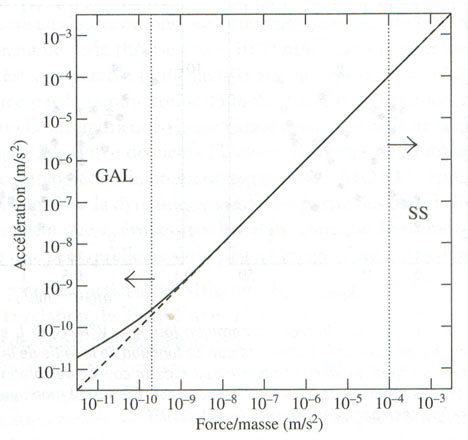
Ce schéma montre la différence entre les deux domaines : à gauche le domaine galactique des très faibles accélérations, à droite celui du système solaire des accélérations fortes. Entre les deux, c’est la fonction x / (1 + x) qui a été choisie pour assurer la continuité.
Dans le mouvement circulaire, l’accélération centripète (en fait l’inertie qui entraînerait l’objet en ligne droite), est :
γc = V2 / r, où V est la vitesse orbitale, et r la distance à l’attracteur. Puisque l’objet est en orbite stable, la force centripète est égale à la force gravitationnelle, donc :
F = m γ2 / γ0 = G M m / r2
On remplace γ par sa valeur centripète :
F = m (V2 / r)2 / γ0 = m V4 / r2 γ0 = G M m / r2
On en tire immédiatement :
V4 / γ0 = G M
et donc :
V4 = G M γ0
Par conséquent, on a bien obtenu ce que l’on cherchait : la vitesse dans ce domaine est une constante.
On peut remarquer en plus que la masse est proportionelle à la quatrième puissance de la vitesse à l’extérieur de la galaxie. Si, comme il est naturel de le penser, la luminosité de la galaxie est proportionnelle à sa masse, on a obtenu le relation de Tully-Fischer.
Ainsi, la relation de Tully-Fisher est naturelle dans cette nouvelle physique. Bien qu’elle ait été trouvée observationnellement avant, on pourrait dire que la théorie la prévoit, puisqu’elle en est une conséquence, alors que la théorie n’a pas été bâtie pour cela.
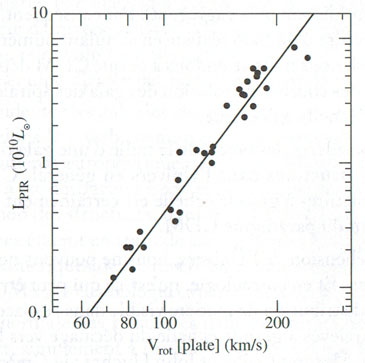
La droite représentée est la prédiction de la théorie MOND. Elle s’adapte parfaitement aux données observationnelles.
Milgrom a basé sa théorie sur l’idée que la modification devait porter sur l’accélération gravitationnelle. Il est maintenant conforté par une observation de 15 ans plus récente.
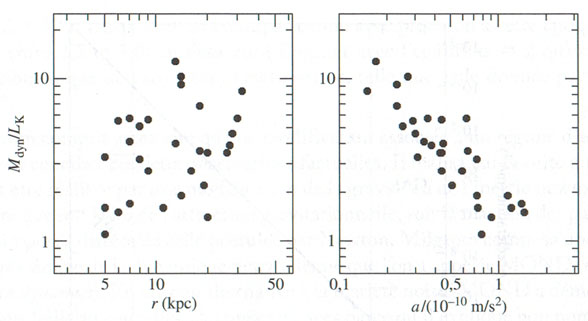
Ces deux schémas montrent le rapport M / L de l’amas de galaxies de la Grande Ourse (spirales seulement), mais classé de deux façons différentes. A gauche, les galaxies sont classées en fonction de leur rayon (taille de la galaxie), et à droite en fonction de l’accélération mesurée à l’extérieur. La masse est la masse newtonnienne.
Il est absolument évident que le classement par taille éparpille les galaxies, alors que le classement par accélération le regroupe selon une diagonale. On constate une dispersion assez importante, ce n’est pas une droite régulière, mais la tendance est claire.
On trouve de petites galaxies avec un rapport M / L faible, d’autres avec un rapport élevé ; de même on en trouve de grandes avec des rapports variés.
A droite, les galaxies dont l’accélération extérieure est relativement élevée ont un rapport M / L faible, celles dont l’accélération est faible ont un rapport élevé.
Le rapport M / L est calculé en considérant la masse des étoiles et la masse du gaz, matière noire exclue bien sûr.
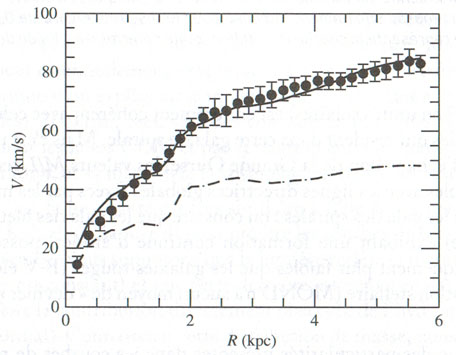
Ce schéma montre la courbe de rotation calculée par MOND, confrontée à la courbe mesurée au radiotélescope de Westerbork, sur les nuages d’hydrogène neutre. On constate le très bon accord entre les deux.
En fait, la théorie s’adapte parfaitement aux galaxies, qu’elles soient à faible ou forte brillance de surface, ce que la théorie CDM ne peut faire. La discordance de CDM vient du fait qu’il faudrait un réglage extrêmement précis entre les densités de matière noire et brillante, pour arriver exactement à ces courbes. MOND n’a pas besoin de cet artifice.
Là est le problème… L’application de MOND aux amas permet, comme on s’y attend, de réduire la quantité de matière noire nécessaire pour justifier les mouvements des galaxies. De réduire, mais pas d’annuler. On passe de 6 fois la masse de matière brillante à 2 fois seulement, mais on n’explique pas tout.
Peut-être faut-il encore un peu de matière noire pour tout expliquer, les neutrinos pourraient éventuellement jouer ce rôle. Mais il reste un problème que MOND ne résoud pas.
Il existe une version relativiste de MOND, nommée TeVeS, mais elle comprend trois champs au lieu d’un… Une belle complexité, à côté de laquelle la Relativité Générale apparaît toute simple !Ni la matière noire, ni la gravité modifiées ne peuvent, chacune séparément, vérifier toutes les observations. Les recherches doivent affiner les résultats, et les théories progresser.
A la recherche de la matière noire H. Sanders, de Boeck 2012
Energie noire, matière noire M. Cassé, Odile Jacob 2004Matière noire et autres cachotteries de l’Univers A. Bouquet, Dunod 2003
---=OO=---