Historique de Marseille
| liens |
le 18/08/17
| Bonne année 2026 ! |
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
|||||
| �� Physique des particules |
| |||||||
… vous commencez à vous sentir comme Sbozo le clown.
Ou Bozo le clownino. N’importino squoi…
Lee Smolin
Rien ne va plus en physique
Dans ce chapitre, vous rencontrerez de nombreux termes nouveaux, dont la consonnance est souvent semblable. Ceci prête naturellement à confusion. Pour bien vous souvenir de ces termes, retenez leur origine étymologique, elle vous sera d’un très grand secours. Vous trouverez à la fin de ce chapitre un résumé de ces étymologies.
Cette simple question cache une difficulté extraordinaire, qui n’est pas totalement maîtrisée aujourd’hui.
La matière est ce que nous connaissons et dont nous sommes faits. Son analyse a pris pratiquement tout le vingtième siècle… Le résultat est le modèle standard de la physique des particules, comprenant 12 particules considérées comme élémentaires. Mais la matière que nous voyons tous les jours n’est pas la seule possible. Les rayons cosmiques se sont avérés constitués en partie de particules instables, qui ne peuvent donc pas subsister dans notre environnement. Elles sont produites dans certaines réactions à haute énergie, et se désintègrent très vite en ne laissant que des particules ordinaires. Nous allons utiliser une approche essentiellement historique.
Les atomes sont les constituants de la matière. Ils ont été imaginés par les philosophes grecs dans l’Antiquité (Démocrite, 4e siècle avant J.C.), qui leur ont donné ce nom : atome vient du grec a : privatif, et du verbe tomein : couper ; littéralement, il signifie insécable. Un atome ne devrait donc pas avoir de structure. Pourtant… L’idée des grecs était que, en coupant en deux un morceau de matière, puis en recoupant en deux l’une des parties, et ainsi de suite, on arriverait à un point où on ne pourrait plus le faire. Le dernier morceau obtenu était donc un atome. Dans ce sens, il reste vrai qu’on ne peut plus couper un atome, sans en changer les propriétés.
Mais les atomes sont complexes, quelques belles expériences l’ont montré.
Ces recherches ont donc montré que l’atome contenait des électrons, particules négatives. Parallèlement à la découverte de l’électron, le noyau a été mis en évidence en 1911 par Ernest Rutherford.
L’expérience de Rutherford a, outre la découvete des noyaux, permis de calculer leur volume. Leur distance donne la taille des atomes, que l’on peut donc comparer à celle des noyaux.
Les atomes sont neutres. Sans cette neutralité, la matière dont nous sommes faits serait chargée, ce qui n’est évidemment pas le cas. Puisqu’ils contiennent des électrons négatifs, il faut qu’une charge positive équivalente soit associée. Il est naturel de penser qu’elle se localise dans le noyau, ce que confirment les expériences. C’est l’attraction électromagnétique entre la charge positive du noyau et les électrons qui lie ces derniers à l’atome.
Le noyau lui-même n’est pas simple. Il est constitué de deux types de particules, les protons et les neutrons. On les appelle génériquement nucléons (du latin nucleus = noyau). Comme leur nom l’indique, les neutrons sont électriquement neutres, alors que les protons portent une charge positive élémentaire (ce qui veut dire la même pour tous ; elle est égale à la charge de l’électron en valeur absolue, on la note donc +e). Un noyau comportant Z protons présentera donc une charge électrique +Z e.
Les protons ont été découverts en 1919 par Rutherford encore, et les neutrons en 1932 par James Chadwick (dans la réaction 4He + 9Be → 12C + n).
En résumé : les atomes sont constitués d’un noyau, comportant Z protons (charge électrique +Z e) et N neutrons, entouré d’un cortège électronique de Z électrons, ce qui lui assure sa neutralité. Le nombre Z de protons est appelé numéro atomique de l’atome. C’est lui qui le caractérise. Le nombre total de nucléons, A = Z + N, est nommé nombre de masse de l’atome. Le nombre de masse est donc, par définition, un entier. Un atome est noté par son symbole, avec en indice son numéro atomique, et en exposant son nombre de masse, les deux du côté gauche :
| atome de carbone ordinaire |
Cortège électronique et neutralité sont réalisés dans des conditions de température (ce qui revient à dire d’énergie) normales (température basse). Ceci constitue le modèle planétaire de l’atome, dû à Niels Bohr, qui le représente avec le noyau semblable au Soleil, et les électrons semblables aux planètes. Il n’est pas exact en Mécanique Quantique, mais se trouve bien utile encore pour essayer de comprendre le fonctionnement de l’atome. On pourra donc l’utiliser, en gardant bien en mémoire les limites de cette représentation.
Masse d’un atome La masse de l’atome est concentrée presque uniquement dans le noyau. Ce dernier contient à peu près autant de neutrons que de protons (ceci est surtout vrai pour les moins lourds).
La masse d’un proton, notée mp, est de 1,7 10-27 kg, c’est-à-dire 1,7 millièmes de milliardième de milliardième de milligramme… La masse du neutron est presque égale. La masse de l’électron est encore bien plus faible : 9,1 10-31 kg, soit 1.836 fois moins que la masse du proton.
Le kilogramme n’étant pas adapté à des masses si petites, on définit l’unité atomique : 1 u = 1,660 540 2 10-27 kg. Pourquoi cette valeur ? Elle est censée représenter la masse d’un nucléon. Pour l’obtenir, on divise par 12 la masse de l’atome de carbone ordinaire (puisqu’il contient 12 nucléons).
La masse d’un atome, exprimée dans cette unité, est nommée masse atomique. La masse atomique du carbone 12 est donc exactement 12 unités atomiques. Cette définition peut paraître curieuse, et en fait elle a varié au cours du temps. Certains chimistes ont pris le noyau d’hydrogène comme référence, d’autres l’oxygène 16 (1/16 de sa masse). Cette variété s’explique par l’énergie de liaison des nucléons dans le noyau : variant d’un atome à l’autre, elle s’ajoute (E = mc2) à la masse atomique, qu’elle modifie légèrement.
La masse atomique est donnée dans le tableau de Mendéléev.
La masse du proton est alors : mp = 1,007 276 470 u. Celle du neutron est 1,008 664 904 u.
On voit que le neutron est légèrement plus massif que le proton. Or les particules se désintègrent toujours de la plus massive vers la moins massive. Ceci est une autre justification de la notion de nucléon, dont le neutron massif est un état excité, et le proton plus léger l’état fondamental.
Il ne faut pas confondre le nombre de masse entier, avec la masse atomique, qui est fractionnaire
Ainsi, un noyau atomique de Z protons contient à peu près 2 Z nucléons (moitié protons, moitié neutrons), sa masse est approximativement de 2 Z mp. La masse des Z électrons est Z × (mp / 1.836). Donc le noyau est :
2 Z mp/ ( Z mp / 1.836) = 2 × 1.836 = 3.672 fois plus massif que les électrons
99,97 % de la masse de l’atome est donc concentrée dans le noyau.
On utilise aujourd’hui un autre système d’unités, mieux adapté aux valeurs des masses. Les physiciens travaillent sur les particules dans de grands accélérateurs, en provoquant des collisions d’une particule projectile sur une cible fixe, ou bien de deux jets de particules opposés l’un contre l’autre. Alors, on détermine les caractéristiques du choc par l’énergie qui a été communiquée aux particules projectiles. Les particules étant accélérées par des champs électriques dans les premiers accélérateurs, on a pris l’habitude de déterminer l’énergie communiquée à une particule par la différence de potentiel qui lui est appliquée.
L’électron-volt (eV) est une unité d’énergie adaptée au monde microscopique. C’est l’énergie cinétique qui est communiquée à un électron accéléré dans le vide par une différence de potentiel de 1 volt.
En unités internationnales, l’eV = 1,602 10-19 joules.
On utilise les multiples : keV (kilo eV = 103 eV), MeV (Mega eV = 106 eV), le GeV (Giga eV = 109 eV), le TeV (Tera eV = 1012 eV).
L’énergie de l’accélérateur de particules le plus puissant jamais construit, le LHC, est actuellement de 7 TeV, mais passera bientôt à 14 TeV.
L’eV est une unité extrêmement petite. Il faut 6 1018 eV (6 milliards de milliards) pour soulever 100 grammes d’un mètre, soit 400.000 fois l’énergie du LHC !
Lorsqu’on dispose, dans un accélérateur, d’une énergie suffisante, on peut créer une paire électron-positron. Ceci en vertu de l’équation si célèbre d’Einstein E = m c2, qui signifie que masse et énergie sont équivalentes : l’une peut se transformer en l’autre, ce sont deux facettes d’une même réalité. Dans l’autre sens, une paire électron-positron peut disparaître, et l’énergie correspondante est créée. En vertu de cette équivalence, les physiciens ont pris l’habitude d’exprimer les masses des particules en unités d’énergie. Puisque E = m c2, on obtient m = E / c2. L’unité choisie est alors le MeV/c2, ou le GeV/c2, mais le plus souvent on note seulement, par abus de langage, MeV ou GeV (en omettant /c2). Si vous trouvez la masse d’une particule exprimée en GeV, rappellez-vous qu’elle est en réalité en GeV/c2.
On peut considérer un atome dont le noyau comporte 1 proton et 1 neutron. Puisqu’il n’a qu’une seule charge électrique, il n’aura qu’un seul électron. Or ce sont les électrons qui déterminent les propriétés chimiques des corps, donc ce sera de l’hydrogène, comme s’il n’y avait qu’un proton seul. Sa masse étant plus grande, on l’appelle hydrogène lourd (lorsqu’il se combine à l’oxygène, il donne aussi de l’eau ; c’est la célèbre eau lourde). On dit que l’hydrogène lourd est un isotope de l’hydrogène. On le nomme plus souvent deutérium, et on lui associe le symbole particulier D. On peut ajouter un second neutron (1 proton, 2 neutrons) ; c’est encore de l’hydrogène, mais plus lourd encore, et nommé Tritium (symbole T). L’hydrogène est le seul élément dont les isotopes portent un nom particulier.
Il existe aussi un atome possédant deux protons et un neutron. Il possède deux charges électriques, il n’a pas les mêmes propriétés chimiques que l’hydrogène : c’est de l’hélium. Et puisqu’il comporte trois nucléons (protons et neutrons), on dit que c’est de l’hélium 3. Il en existe un autre : l’hélium 4 qui est le deuxième isotope de l’hélium. Ce dernier comporte bien sûr deux protons, sinon ce ne serait pas de l’hélium, et deux neutrons qui le rendent différent de l’hélium 3 : plus lourd, mais avec les mêmes propriétés chimiques. Nous verrons toutefois plus loin qu’ils ont des propriétés physiques différentes aussi.
Dans le tableau de Mendéléev, on trouve pour la masse atomique du chlore la valeur 35,5. La masse du proton étant 1,007 on pourrait penser que les masses atomiques, multiples entiers approximatifs de cette valeur resteraient proches d’un entier. Pour le chlore, ce n’est évidemment pas le cas. La raison est simple : il n’y a pas qu’un seul chlore, il y en a 24 (24 isotopes) ! Mais seulement 2 sont présents à l’état naturel sur Terre, les isotopes 35 et 37. L’isotope 36 est radioactif, et il est produit par divers mécanismes en petite proportion, que l’on peut négliger. La masse atomique 35,5 résulte donc du mélange des deux isotopes 35 et 37 : l’isotope 35 (18 neutrons, 75,78 % du mélange, masse atomique 34,9688 u) et l’isotope 37 (20 neutrons, 24,22 % du mélange, masse atomique 36,9659) : (34,9688× 75,78 + 36,9659× 24,22) / 100 = 35,4525.
A chaque fois que vous trouverez un poids atomique qui s’écarte nettement d’un entier dans le tableau de Mendéléev, vous saurez qu’il s’agit d’un mélange d’isotopes.
Les atomes sont minuscules. La taille d’un atome est celle de son cortège électronique, soit de l’ordre de 10-10 m, i.e. un dix milliardième de mètre. On utilise comme unité de longueur dans le domaine atomique, le fermi (noté fm) qui vaut :
1 fm = 10-15 m
1 millionième de milliardième de mètre
Un atome a donc une taille de l’ordre de 100.000 fermis, alors que le noyau ne mesure que quelques fermis.
Le noyau est 100.000 fois plus petit que l’atome
Remarque : la notion de taille d’un noyau atomique a-t-elle un sens ? Il est impossible de photographier un noyau pour en mesurer le diamètre. On utilise une autre technique, on le bombarde avec des projectiles suffisamment petits (?). La plupart continuent leur route sans être perturbés. Mais certains heurtent le noyau et rebondissent dessus : ils sont diffusés. Par analogie, imaginez que vous envoyiez des fléchettes sur une cible, les yeux bandés. Le bruit de la fléchette qui touche la cible vous permet seulement de compter combien d’entre elles ont atteint le but. En supposant que vous envoyiez beaucoup de fléchettes, distribuées aléatoirement dans la région de la cible, le rapport de celles qui ont touché sur le nombre total vous permettra de déduire la surface de la cible par rapport à celle du mur, donc le diamètre de la cible. Le problème est que, selon le type de fléchette utilisé (neutron, proton, électron), les résultats varient quelque peu. Mais ici, l’ordre de grandeur nous suffit.
Quand à l’électron, on ne sait pas trop quelle est sa taille exacte, car on manque de moyens pour le mesurer. Mais on sait qu’il est plus petit que 10-18 m, soit 10-3 fm. L’électron est 1.000 fois plus petit que le noyau, et 108 (cent millions de) fois plus petit que l’atome…
Si le noyau d’un atome d’hydrogène (un proton) mesurait 1 mm de diamètre (une tête d’épingle), l’électron mesurerait moins d’un micromètre (une bactérie), et tournerait autour du proton à 100 m.
A cette même échelle, le noyau aurait une masse de 170 millions de tonnes, l’électron de 9.000 tonnes.
Une conséquence de ces valeurs est que l’atome est totalement vide ! Le volume étant proportionnel au cube du rayon, et le rapport entre le diamètre du noyau et celui de l’atome étant de 10-5, le rapport de leurs volumes est de (10-5)3 = 10-15 soit 1 millionième de milliardième. Ou encore 99,9999999999999 % du volume de l’atome est vide…
L’analogie ci-dessus donne à réfléchir : tout l’équilibre de la matière qui nous entoure, et dont nous sommes faits, est réalisé par les électrons, qui sont tellement petits. La stabilité d’une naine blanche aussi repose sur eux… Petits, mais efficaces !
Schéma des deux atomes les plus simples et les plus légers (isotopes les plus courants) :
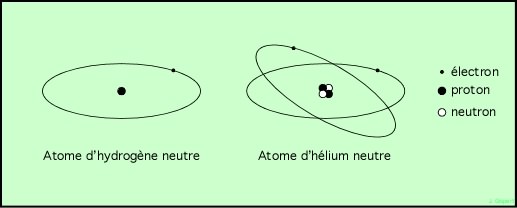
Représentation de deux atomes à l’aide du modèle planétaire
Evidemment, les proportions ne sont pas respectées, et de loin ! Ces schémas représentent le modèle planétaire de l’atome de Bhor. Conçu avant la Mécanique Quantique, ce modèle classique permet de bien représenter les niveaux d’énergie électronique de l’hydrogène, qui expliquent très bien son spectre, depuis l’infrarouge jusqu’à l’ultraviolet. La représentation d’orbites bien définies est fausse en Mécanique Quantique, mais bien pratique pour la compréhension.
C’est le nom que l’on donne à l’ensemble des électrons qui, liés à un noyau, assurent la neutralité de l’atome. Il est responsable des propriétés chimiques des atomes, et aussi de nombreuses propriétés physiques, comme la fluorescence. L’étude de l’atome complet, avec ses électrons, ne fait pas partie au sens strict de la physique nucléaire. Elle est traitée dans le chapitre consacré à la lumière.
D’où vient la stabilité de ces structures ? Pourquoi les nucléons restent-ils ensemble, et pourquoi les électrons s’attachent-ils aux noyaux ? Parce qu’il existe des forces qui les réunissent.
Historiquement, la notion de force a été introduite par Newton pour expliquer que le Soleil attire la Terre, et lui permet ainsi de rester en orbite autour de lui. Cette notion de force, assez anthropomorphe, est tombé en désuétude. Elle a eu sa part dans les tentatives d’explication du monde, mais elle paraîssait un peu mystérieuse par son action à distance et instantanée. Elle est remplacée aujourd’hui par la notion relativiste d’interaction, qui est portée par un champ, lequel se propage à vitesse finie (celle de la lumière) par des ondes. Un champ matérialise la présence, en chaque point de l’espace, de l’influence de la source de l’interaction.
Nous allons donc voir quelles sont les interactions en cause. Elles sont au nombre de quatre.
Depuis l’Antiquité, l’interaction électromagnétique est connue, sous ses deux formes : l’aimant naturel (magnétite, Fe3O4), capable d’attirer le fer, et l’ambre (elektron en grec) qui, frotté, attire les corps légers comme des poussières. L’aimant agit par l’interaction magnétique, l’ambre par l’interaction électrique. Ces deux formes, pourtant fort dissemblables en apparence (l’aimant naturel n’a pas d’action sur l’ambre), ont été unifiées par Maxwell, qui en a fait l’interaction électromagnétique. La justification de cette unification est donnée par le moteur électrique, la dynamo, etc. Dans le moteur électrique, un courant (électricité) produit un champ magnétique (magnétisme) qui donne la force motrice ; dans la dynamo, c’est un aimant qui tourne à l’intérieur d’une bobine de fil électrique ; le champ magnétique variant à cause de la rotation, induit un courant électrique dans le fil. Donc, courant électrique et champ magnétique s’induisent l’un l’autre.
L’interaction électromagnétique a été étudiée à propos de la lumière, et vous pouvez vous y reporter. Elle agit entre particules portant une charge électrique, c’est-à-dire protons et électrons (il existe d’autres particules chargées). C’est elle qui maintient les électrons autour du noyau, en nombre égal à celui des protons, ce qui assure la neutralité électrique de l’atome.
Pour expliquer la liaison durable entre les nucléons, il faut une interaction qui agisse tout aussi bien sur les neutrons que sur les protons.
Les neutrons étant neutres, l’interaction électromagnétique ne convient pas. La gravité est bien trop faible, nous le verrons plus loin. On doit donc invoquer une interaction spécifique, possédant des propriétés très particulières : dans un noyau d’hélium, il y a deux protons pratiquement collés l’un à l’autre. Les deux protons portant chacun une charge électrique positive, se repoussent très violemment. Ils devraient par conséquent s’éloigner brutalement. Pour que ce ne soit pas le cas, l’interaction qui les colle doit être beaucoup plus forte, d’où son nom d’interaction forte. Elle doit agir indifféremment sur les protons et les neutrons, puisque ces derniers sont fixés dans le noyau. Mais pour que le noyau d’hélium soit stable, il faut ajouter au moins un neutron, qui participe à l’interaction forte et retient les deux protons, sans augmenter leur répulsion puisqu’il est neutre. Sans lui, ils se sépareraient. C’est pourquoi l’hélium 2 (2 protons, pas de neutrons) n’existe pas.
Si l’interaction forte portait à grande distance, tous les nucléons devraient se réunir en un seul noyau atomique ! l’Univers serait un trou noir… Ce n’est manifestement pas le cas, et ceci ne s’explique qu’en admettant que l’interaction forte est à très courte portée. En fait, son domaine d’influence ne dépasse pas les dimensions du noyau atomique, car c’est justement lui qui les fixe : si la portée de l’interaction forte était plus grande, les noyaux atomiques seraient plus gros !
L’interaction forte est donc très forte à moins d’un fermi (10-15 m), mais pratiquement inexistante au-delà.
Cette courte portée a deux implications importantes :
Nous reviendrons plus loin sur l’interaction forte, dont les propriétés sont assez surprenantes, et dont l’explication met en jeu des éléments que nous verrons bientôt.
On observe des transformations de particules : par exemple, la désintégration du neutron citée plus haut : n → p + e- + ν’e (où ν’e est l’antineutrino électronique). Le neutron étant électriquement neutre, il n’y a pas de charge électrique avant la réaction, c’est-à-dire à gauche de la flèche. Il ne doit pas y en avoir non plus à droite, pour satisfaire au principe fondamental de conservation de la charge. Or le proton qui remplace le neutron porte une charge positive. Celle-ci doit donc être annulée par une charge négative de même valeur absolue -e. C’est la création d’un électron qui y pourvoit. Dans cette désintégration, on peut faire aussi le bilan énergétique. Et là, ce fut la catastrophe ! Le bilan n’était pas équilibré, on trouvait plus d’énergie avant la réaction qu’après. Où était passée la différence ? La conservation de l’énergie est un autre principe fondateur de la physique, et il doit être respecté. Alors, Wolfgang Pauli a eu l’idée de concevoir une nouvelle particule, qui emporterait l’énergie manquante. Cette particule devait être électriquement neutre, puisque l’équilibre électrique est déjà réalisé. D’autre part, le bilan des masses montrait un équilibre entre les deux termes de la réaction, donc la masse de cette nouvelle particule devait être, sinon nulle, tout au moins extrêmement faible, plus faible que les erreurs de mesure. Cette particule a été nommée neutrino (petit neutre), par Enrico Fermi. C’est le ν’e de la réaction précédente.
Mais cette réaction couramment observée, posait un problème de fond : ni l’interaction électromagnétique, ni l’interaction forte n’explique ces changements. Il fallait invoquer une nouvelle interaction, nommée interaction faible, car les mesures ont montré qu’elle était encore plus faible que l’interaction électromagnétique. Elle intervient dans toutes les réactions où figurent des électrons et des neutrinos.
La quatrième interaction est connue depuis toujours, mais sans le savoir, comme la prose de Mr Jourdain : la gravité qui nous retient au sol est tellement naturelle et évidente, que peu de gens imaginent qu’il faut une force pour nous maintenir ainsi au sol.
L’interaction électromagnétique et la gravitation présentent une caractéristique commune : elles ont une portée infinie. Les deux sont additives. Si on place deux électrons au lieu d’un, on obtient une force électromagnétique double. Deux planètes attirent deux fois plus qu’une seule. Mais elles diffèrent aussi par leur intensité : l’interaction gravitationnelle est 1034 fois plus faible que l’interaction électromagnétique. Pour elle, l’union fait vraiment la force ! Tous les atomes qui constituent le Soleil s’unissent pour créer une force gravitationnelle capable d’enchaîner toutes les planètes… Une raison est que les masses sont toutes positives ! Elle s’additionnent, et ne se neutralisent pas, alors que les charges électriques présentent deux signes, l’un annulant l’autre. Bien qu’elle soit de portée infinie, l’interaction électromagnétique est limitée par la neutralité de la matière.
L’interaction gravitationnelle est tellement faible, qu’elle n’a strictement aucune influence sur les particules élémentaires, au niveau microscopique. Au niveau astronomique et cosmologique par contre, elle est la seule sensible, car son aspect additif prend le pas sur toutes les autres (d’ailleurs, la portée des autres est négligeable, car les deux interactions nucléaires forte et faible ont une portée très courte, et l’électromagnétisme a une portée infinie, mais limitée pratiquement par la neutralité globale de la matière).
Dans cette remarque, on voit poindre les distinctions entre les domaines :
Ces 4 interactions sont les seules nécessaires pour expliquer toute la physique actuelle, depuis les particules jusqu’à l’Univers dans son ensemble (et ceci jusqu’à preuve du contraire).
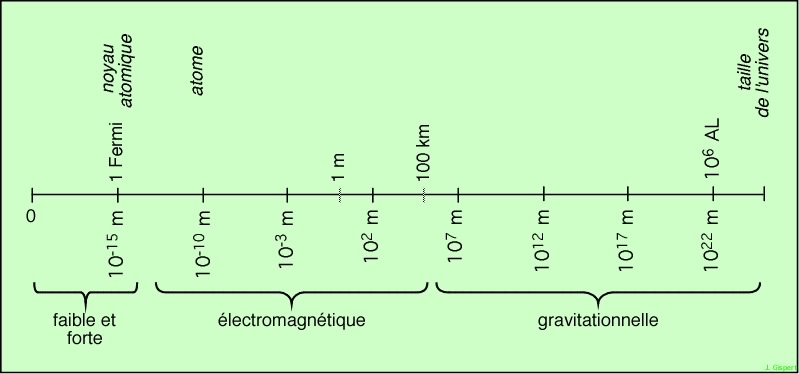
Portée des interactions
Les réactions chimiques consistent à coller des atomes complets, la colle étant l’interaction électromagnétique. Ce sont donc les électrons qui entourent le noyau qui sont responsables de la formation des molécules (agrégats d’atomes).
Par contre, les réactions nucléaires portent sur les constituants des noyaux (protons et neutrons). La force qui les lie est l’interaction forte.
La chimie se place donc à une échelle de distances 100.000 fois plus grandes que la physique nucléaire. Mais l’énergie mise en jeu est aussi très différente. L’énergie typique d’une réaction chimique se compte par un petit nombre d’électron-volts. Les réactions nucléaires jouent sur des MeV (millions d’électron-volts).
La fusion construit des noyaux lourds à partir de noyaux plus légers (fusion de l’hydrogène, de l’hélium, du carbone…) ; la fission détruit des noyaux lourds pour restituer des noyaux plus légers (fission de l’uranium…).
La fusion de l’hydrogène donne 27 MeV par noyau d’hélium produit ; la fission de l’uranium donne de son côté 200 MeV par atome brisé. L’énergie nucléaire est donc des dizaines de millions de fois plus grande que l’énergie chimique.
Ces données ne doivent pas faire croire que la fission est plus énergétique que la fusion. Pour produire 27 MeV, la fusion utilise 4 protons, donc une masse de 4 mp. Ce qui fait 27 / 4 = 6,75 MeV par nucléon (par unité de masse). Pour produire 200 MeV, la fission brise un atome d’uranium 235, de masse 235 mp. Donc 200 / 235 = 0,85 MeV par nucléon seulement. Par unité de masse, la fusion de l’hydrogène produit donc 8 fois plus d’énergie que la fission de l’uranium.
Le tableau ci-dessous permet de comparer grossièrement les distances et les énergies dans les deux domaines, chimique et nucléaire (atomes pour la chimie, nucléons pour les noyaux atomiques). Les énergies de liaison sont aussi les énergies produites par les réactions :
| chimie | physique nucléaire | |
|---|---|---|
| distance | 100.000 fm | 1 fm |
| énergie | 1 eV | 100.000.000 eV |
On a montré expérimentalement que la lumière est à la fois corpusculaire (le corpuscule est le photon, qui explique l’effet photoélectrique, le rayonnement du corps noir, la diffusion Compton…) et ondulatoire (l’onde électromagnétique, qui explique les interférences…). Pourquoi l’interaction électromagnétique serait-elle la seule à associer onde et corpuscule ? En fait, pourquoi toute interaction ne serait-elle pas portée par une particule spéciale ?
Ce pas a été franchi par Louis de Broglie : il a supposé que toutes les particules ont une onde associée, et réciproquement. Ce point de vue a l’avantage supplémentaire de limiter la vitesse de propagation de l’interaction. Puisque c’est une particule, elle ne peut se déplacer à une vitesse supérieure à celle de la lumière.
La Mécanique Quantique, basée sur ce principe, et la Relativité, sont les deux grandes théories physiques qui ont occupé les physiciens pendant tout le XXe siècle, et ce n’est pas fini.
Chaque interaction se propage comme une onde, c’est ainsi qu’elle agit à distance, comme la lumière. Par analogie avec la lumière, et en suivant Louis de Broglie, on considère que les ondes qui portent les autres interactions ont aussi une particule associée, dite médiatrice. On aura donc deux types de particules : les particules de matière, et les particules d’interaction. Qu’est-ce qui les différencie ?
C’est une propriété que possèdent les particules, et que l’on associe, pour tenter de l’expliquer, à la rotation de la particule. Image qui trouve vite sa limite, mais qui a tout au moins donné un nom à cette propriété : le spin. La limitation vient du fait que le spin est quantifié -ce qui signifie qu’il ne peut prendre que certaines valeurs- par opposition à la Physique Classique, qui admettait pour toute propriété une continuité de valeurs.
Si le spin était une vitesse de rotation, il pourrait prendre n’importe quelle valeur, comme 1,753 par exemple. C’est le cas pour une toupie, dont la vitesse diminue régulièrement et continuement.
Mais le spin ne peut prendre comme valeurs que des entiers : 0, 1, 2,… -1, -2…. ou des demi-entiers : 1/2, 3/2 … -1/2, -3/2 …
Le spin différencie deux types de particules :
Le boson médiateur de l’interaction électromagnétique est le photon. Pour l’interaction faible, il y a trois bosons médiateursnbsp;: le W+, le W- et le Z0. Et pour l’interaction forte, il y a 8 gluons (explication plus loin).
Tous ces bosons ont été observés, leur existence est donc prouvée. Enfin, pour l’interaction gravitationnelle, le boson médiateur est le graviton, mais on n’a aucune preuve observationnelle de son existence. Il n’est pas étonnant que ce soit la dernière qui résiste, tels certains gaulois, puisqu’elle est associé à la moins intense de toutes les interactions. Théorisée par Einstein, dans la Relativité Générale, l’interaction gravitationnelle s’adapte à l’échelle macroscopique, mais non à l’échelle microscopique, car elle est incapable de modéliser les fluctuations de l’espace-temps qui s’y produisent.
La Mécanique Quantique est surprenante, car à l’échelle microscopique des particules, la Nature n’a pas le même comporterment qu’à notre échelle macroscopique. Il est d’ailleurs possible que les notions que nous utilisons pour décrire les objets, découlant de notre expérience quotidienne, ne soient pas adaptés à la description des particules. Mais si c’est le cas, ce sera probablement l’avancée théorique qui nous permettra d’améliorer ces descriptions.
On considère le montage des trous de Young. On lance des électrons en direction de l’écran percé, et on relève l’intensité du faisceau projeté sur un écran placé derrière. On y observe des franges d’interférence. Comment savoir si un électron particulier est passé par le trou du haut ou par celui du bas ? Imaginons qu’on l’éclaire avec une source lumineuse pour le voir passer. L’énergie du photon qui éclaire est h ν. Si elle est assez haute, elle nous renseigne précisément sur la position de l’électron, mais elle le perturbe (elle lui cède son énergie) et l’électron n’interférera plus : on sait d’où il vient, mais on ignore ce qu’il aurait fait si on l’avait laissé tranquille… Si on baisse l’énergie du photon, on baisse aussi la précision, la finesse de l’image. Lorsque la perturbation devient ainsi acceptable, on constate que l’image est assez floue pour qu’on ne sache plus par quel trou est passé l’électron ! Les interférences se produisent, mais on ne sait pas d’où il vient !!!
C’est cette théorie de la perturbation qui est à la base du principe d’incertitude : les moyens pour observer une particule microscopique la perturbent profondément. A contrario, sur un objet macroscopique, l’énergie cédée par quelques photons n’est en aucune manière capable de le perturber.
Le principe d’incertitude s’applique d’abord aux mesures de la position et de l’impulsion d’une particule (l’impulsion est le produit de la masse par la vitesse). Il stipule que :
![]()
où Δx est la variation de position, et Δpx la variation d’impulsion (la relation s’applique pour le mouvement dans la direction x, et pour l’impulsion dans cette même direction). Ceci signifie que si on connait précisément x (Δx petit), alors on connait mal px (Δpx grand, donc erreur sur la vitesse grande), et réciproquement. On ne peut connaître les deux simultanément avec une bonne précision. Mais les particules doivent obéir à cette règle : si on les rapproche, Δx diminue, et Δpx doit augmenter (autrement dit la vitesse doit augmenter, puisque p = m v). C’est ce qui explique la stabilité des naines blanches ou des étoiles à neutrons, l’augmentation de vitesse entraînant une augmentation de pression.
Principe d’incertitude d’Heisenberg
L’animation présente la courbe des valeurs minimales satisfaisant le principe d’incertitude, soit Δx Δpx = hBarre. Elle représente Δx = hBarre / Δpx, ou bien Δpx = hBarre / Δx.
L’une des valeurs étant fixée, la valeur minimale de l’autre s’en déduit donc immédiatement, et se voit sur la courbe.
Deux curseurs, en bas de la fenêtre, permettent de choisir les valeurs de Δx ou Δpx. Vous constaterez que toute variation imposée à l’un entraîne une variation de l’autre en sens inverse, de telle sorte que le produit Δx Δpx soit toujours égal à hBarre. Vous vérifierez cela en observant les valeurs données dans le haut de l’animation.
Par exemple, fixons Δx = 0,288. Δpx prend la valeur 3,467, telle que leur produit soit égal à 1. Pour que le principe d’incertitude soit satisfait, il faut que Δpx ≥ 3,467.
Les deux petits traits sur la courbe indiquent les valeurs de Δx (jaune) et Δpx (vert). Vous pouvez cliquer sur ces traits. Cliquez par exemple sur le jaune (Δx). Vous fixez Δx, et les valeurs de Δpx qui satisfont au principe d’incertitude correspondent à la partie de courbe dessinée en vert. Ce sont les valeurs de Δpx supérieures à la valeur minimale définie par le trait vert. Toute valeur de Δpx correspondant à la partie verte est acceptable.
La contrainte Δpx ≥ valeur minimale possible apparaît.
Le nom du principe est mal choisi. Il semble indiquer que l’on n’est pas capable de faire des mesures précises, et ce n’est pas le cas. Le problème est bien plus fondamental. Prenons un exemple compréhensible : nous voulons mesurer la fréquence d’une onde, par exemple le son d’une sirène. Pour mesurer la fréquence, il faut connaître l’intensité du son à plusieurs instants différents ! Plus la durée de la mesure est grande, plus grande est sa précision. Pour une durée très brève, nous devrons nous contenter d’une mesure grossière. Si vous voulez imager ceci, regardez une sinusoïde à travers une fente. Si la fente est large, vous en voyez beaucoup, et la mesure de la fréquence est facile. Si la fente est étroite, vous n’en voyez que très peu, et il faut imaginer le reste, ce qui rend la mesure bien moins précise. Ce problème est donc inhérent aux ondes, et puisque toute particule est décrite par son onde associée, elle est soumise à ce principe.
Mathématiquement, on considère deux grandeurs que l’on souhaite mesurer, et qui sont nommées observables. A chacune est associé, en Mécanique Quantique, un opérateur (fonction mathématique). Deux observables A et B sont dits conjugués si leurs opérateurs ne commutent pas : AB - BA ≠ 0. C’est le cas entre autres de la position et de l’impulsion, du moment cinétique et de la position angulaire… C’est aussi le cas de l’énergie et du temps, mais pour une autre raison, car il n’existe pas d’opérateur correspondant au temps.
On préfère parfois nommer ce principe principe d’indétermination. Il est même élevé en théorème, car il se déduit logiquement des bases de la Mécanique Quantique.
Le principe d’incertitude s’applique aussi au domaine macroscopique, mais les limitations qu’il impose sont très très en-dessous des erreurs de mesures, même les plus précises. Il suffit, pour s’en persuader, de faire le calcul pour une voiture par exemple… Toutefois, des expériences très fines sont faites maintenant, et la vérification a pu être obtenue pour des objets aussi gros qu’une molécule de fullerène (C60, formée de 60 atomes de carbone).
Imaginons que le vide soit, comme on le pensait à la fin du XIXme siècle, l’absence de toute chose (matière et énergie). Prenons un point quelconque dans ce vide. Puisqu’il n’y a rien, l’énergie y est, et y reste, nulle : E = 0 à tout instant. Entre deux instants quelconques t1 et t2, la variation d’énergie est donc ΔE = 0 - 0 = 0. On peut faire des mesures aussi rapprochées que l’on veut, donc avec t2 pratiquement égal à t1. Alors, ΔT = 0. Et le produit ΔE ΔT est inférieur à hBarre !
Cette hypothèse d’espace totalement vide n’est donc pas possible : l’espace contient donc de l’énergie qui fluctue au cours du temps. En un point donné, l’énergie varie constamment. La conséquence immédiate est que, lorsqu’une fluctuation d’énergie est supérieure à la masse d’un couple particule-antiparticule, ce couple peut être créé. Mais pour respecter le principe d’incertitude, et permettre à l’énergie de retourner à une faible valeur, ce couple doit immédiatement s’anihiler en restituant son énergie de masse.
On conçoit donc aujourd’hui le vide quantique comme une mousse dans laquelle se créent et se détruisent constamment des paires de particules…
L’état quantique d’une particule est défini par son énergie, son spin… toutes propriétés qui la caractérisent. Il traduit donc le fait que les particules obéissent à la statistique correspondant à leur type : statistique de Fermi-Dirac pour les fermions, de Bose-Einstein pour les bosons.
La Mécanique Statistique décrit un gaz comme un ensemble de particules, dont elle détermine les propriétés macroscopiques (pression, masse volumique…), par l’application des lois physqiues, essentiellement de la Mécanique Quantique, sur ses composants microscopiques. La thermodynamique, théorie empirique, est ainsi retrouvée à partir de concepts bien plus fondamentaux.
Pour apréhender un très grand nombre de particules, il est impossible de représenter et de mettre en équation les paramètres de chacune d’entre elles. On caractérise alors par exemple, dans un gaz, la proportion d’atomes ou de molécules (les constituants) possédant à tout instant une certaine vitesse. La théorie détermine ainsi quelle proportion d’atomes possède une vitesse donnée.
Pour les photons, on peut déterminer de cette manière combien d’entre eux ont une énergie donnée, dans un milieu à la température T. Ils se comportent collectivement selon la statistique de Bose-Einstein. A partir de là, le physicien indien Satyendra Nath Bose a retrouvé la loi du rayonnement du corps noir (loi de Planck).
Les photons sont des bosons, et peuvent donc marcher au pas (statistique de Bose-Einstein) : l’application la plus connue est le laser. Dans un rayon laser, tous les photons ont exactement la même couleur, et sont en phase. Lorsque des bosons se mettent tous dans le même état, on parle de condensation de Bose-Einstein. L’association de "condensation" et de "Bose" dans cette locution peut aider à mémoriser la distinction entre les deux statistiques.
Sur le plan mathématique, la différence entre bosons et fermions vient d’une symétrie. L’onde associée à une particule (onde de de Broglie) est décrite par une fonction d’onde Ψ, déterminée par Schrödinger. Pour deux particules identiques x et y, et deux points p1 et p2, la fonction est Ψ(x, y). Le carré de sa norme |Ψ(x, y)|2 donne la probabilité de trouver x en p1, et y en p2. |Ψ(y, x)|2 donne la probabilité de trouver y en p1, et x en p2. Puisque les particules sont identiques, ces probabilités sont égales : |Ψ(x, y)|2 = |Ψ(y, x)|2. Cette égalité se réalise dans deux cas différents :
| Ψ(x, y) = Ψ(y, x) | la fonction d’onde est symétrique | bosons | spin entier |
| Ψ(x, y) = - Ψ(y, x) | la fonction d’onde est antisymétrique | fermions | spin demi-entier |
Le lien entre le spin et la statistique est démontré par le théorème spin-statistique, qui est de nature relativiste (dans la théorie non-relativiste décrite par l’équation de Schrödinger, le spin est indépendant de la statistique, ce que l’expérience ne confirme pas). Il n’y a pas d’explication simple à donner. Il faut l’admettre. | |||
La fonction d’onde symétrique signifie qu’on peut échanger deux particules (identiques) sans changer les propriétés globales. C’est le cas dans un rayon laser où tous les photons jouent exactement le même rôle. Par contre, si on échange deux fermions, la fonction d’onde étant antisymétrique, le signe du résultat est changé, et certaines propriétés physiques sont modifiées également.
Le comportement collectif des bosons et des fermions est fondamentalement différent, et présente une importance capitale en astrophysique.
S’il vous plait, dessine-moi un boson ! Le Petit Prince, Antoine de Saint Exupéry (presque…) |
 |
Dans le monde microscopique des particules, il n’est donc pas possible de définir exactement ce que fera une particule. On peut seulement donner la probabilité qu’elle ait un comportement déterminé. Chaque type de particule obéit ainsi à une loi statistique particulière. Et les lois associées aux bosons et aux fermions sont radicalement différentes. Ces deux lois statistiques portent les noms des physiciens qui les ont découvertes :
| bosons (interaction) | spin entier | statistique de Bose-Einstein |
| fermions (matière) | spin demi-entier | statistique de Fermi-Dirac |
On dit que les particules de matière obéissent à la statistique de Fermi-Dirac, alors que les particules d’interaction obéissent à la statistique de Bose-Einstein.
Le principe d’exclusion de Pauli stipule que :
Remarque importante : le principe d’exclusion s’applique pour des particules ayant le même état quantique. En particulier donc, il ne s’applique qu’à deux fermions IDENTIQUES. Par exemple, à deux protons, à deux neutrons, mais pas à un proton et un neutron, qui sont des fermions différents. Par exemple, on peut très bien grouper deux protons et deux neutrons, pourvu que chaque paire soit dans un état de spin différent. C’est la particule alpha, noyau d’hélium (un proton de spin up, un proton de spin down, un neutron de spin up, un neutron de spin down). Et cette propriété assure sa grande stabilité, puisque ses quatre composants sont tous dans l’état d’énergie minimum !
Lorsque deux fermions identiques (deux protons, ou bien deux neutrons, ou bien deux électrons…) se trouvent au même endroit (même position, Δx négligeable), ils ne peuvent y rester. En effet, s’ils restent proches, c’est que leur vitesse relative est négligeable, donc que Δpx est proche de 0. Alors, le produit Δx Δpx est inférieur à hBarre, violant le principe d’incertitude. Pour le respecter, il faut que Δpx soit très grand, donc que la vitesse relative soit très grande. Par conséquent, l’un des deux fermions s’échappe à grande vitesse de l’autre, vitesse d’autant plus élevée que la proximité était grande. Et dans cette fuite, il heurte d’autres particules, auxquelles il confère une vitesse. Ceci produit donc une pression, nommée pression de Fermi.
La propriété remarquable de la pression de Fermi, est son indépendance de toute source d’énergie : elle est produite par un principe quantique, qui dépend de la nature des particules seulement. Elle est donc éternelle, pour autant que les particules elles-mêmes le soient.
La pression de Fermi explique la stabilité des naines blanches et des étoiles à neutrons : les naines blanches sont stabilisées par la pression de Fermi des électrons, les étoiles à neutrons par celle des neutrons, ces deux types de particules étant des fermions. Une fois le stade de naine blanche atteint, l’étoile n’a plus besoin d’énergie pour maintenir son équilibre contre la gravité : elle est devenue éternelle. Il en est de même des étoiles à neutrons, qui sont bien plus condensées que les naines blanches, et dont l’équilibre est assuré par les neutrons, beaucoup plus lourds que les électrons.
Mais la pression de Fermi a des limites : c’est la vitesse des fermions qui l’assure, et celle-ci ne peut en aucun cas dépasser ni même atteindre celle de la lumière. Plus la gravité écrase, plus les fermions se rapprochent, et plus leur vitesse augmente. Si la gravité devient assez forte pour que les neutrons approchent la vitesse de la lumière, la rupture n’est pas loin. La masse maximum d’une étoile à neutrons est donc celle pour laquelle le principe d’incertitude amène les neutrons exactement à la vitesse de la lumière. Au-delà, la pression de Fermi ne peut plus augmenter, et l’écrasement de l’étoile est inéluctable : elle devient un trou noir.
Dans les naines blanches, ce sont les électrons qui atteignent la limite de pression lorsqu’ils approchent la vitesse de la lumière. Mais une naine blanche qui s’effondre a encore la ressource de freiner l’écrasement par les neutrons… La masse maximale d’une naine blanche est la masse de Chandrasekhar.
Nous avons considéré jusque là des particules isolées. Si on considère maintenant des associations de plusieurs particules simples, comme par exemple un noyau d’hélium, que pourrait-on dire de leur comportement ? La règle est simple :
Une particule composée est un fermion si elle comprend un nombre impair de fermions et un nombre quelconque de bosons. Sinon, c’est un boson.
Ceci est facile à comprendre si on envisage la fonction d’onde de la particule composée, qui s’obtient par l’association des fonctions d’onde des constituants : pour chaque fermion ajouté, elle change de signe. Donc, s’il y en a un nombre impair, le signe résultant sera changé (la particule sera donc un fermion), inchangé sinon (ce sera un boson). Et pour chaque boson, le signe est conservé, il peut donc y en avoir un nombre quelconque.
Conséquences :
C’est Einstein qui a découvert ces conséquences. Il en a déduit que ces particules, refroidies, devraient se retrouver toutes dans un même état quantique (condensation de Bose-Einstein). Ceci a été vérifié plus tard sur l’hélium 4 qui, au-dessous de 2,18 Kelvins, est superfluide. L’hélium 3 étant un fermion, ne peut être superfluide.
Paul Dirac a réécrit l’équation de Schrödinger (l’équation qui donne la fonction d’onde en Mécanique Quantique) pour la rendre relativiste. Lorsqu’il a cherché les solutions de son équation (énergie), Dirac a trouvé que le carré de l’énergie avait une certaine valeur E2 = v. Alors, l’énergie vaut E = ± √v, soit deux valeurs de signe opposé (E = +√v, E = -√v). La solution négative correspondait à l’électron, mais la solution positive ne correspondait apparemment à rien. Dirac a imaginé qu’il existe une particule semblable à l’électron, mais de charge positive. Il l’a nommée positron (ou positron), ou anti-électron.
Le positron a été découvert expérimentalement peu après par Anderson.
Dans certaines réactions, un positron est émis. S’il est pris dans un champ magnétique, il parcourt une trajectoire circulaire, comme l’électron, mais à l’envers. Ce sens opposé permet de déterminer sa charge positive.
Le même rayon de sa trajectoire (à la même énergie bien sûr) montre par ailleurs qu’il a la même masse.
Dirac a généralisé son idée en supposant que toute particule pourrait avoir son antiparticule. La suite lui a donné raison.
La caractéristique essentielle d’un couple particule-antiparticule et de pouvoir s’annihiler : lorsqu’elles se rencontrent, elles disparaissent, et laissent à leur place une paire de photons. Pour que l’énergie soit conservée, il faut que l’énergie des deux photons représente la somme des masses des deux particules. C’est l’équation d’Einstein E = m c2 qui en rend compte. Prenons l’exemple courant de l’électron : sa masse, égale à celle du positron, est de 511 keV/c2. L’anihilation d’une paire électron-positron donne deux photons tels que E = h ν = 511 keV. Des annihilations de ce genre se produisent dans l’Univers, car des positrons sont produits dans certaines réactions énergétiques. Lorsqu’un positron rencontre un électron (qui sont partout), ils s’annihilent et produisent deux photons de 511 keV. On les observe effectivement. Réciproquement, si on dispose d’une énergie au moins égale à cette valeur, il est possible de créer une paire électron-positron.
On note que, lorsqu’un électron et un positron s’annihilent, la charge négative du premier, et la charge positive du second, s’annulent : -e + e = 0. Si la charge d’une particule est nulle, elle peut être sa propre anti-particule puisque -0 + 0 = 0. Le photon par exemple, particule neutre, est sa propre anti-particule.
Dans le cas des fermions, on parle de particule de Majorana (du nom d’Ettore Majorana) pour ceux qui sont leur propre antiparticule ; ou bien de particule de Dirac, pour celles dont l’antiparticule est distincte. A l’heure actuelle, on ne connait pas de particules de Majorana (le photon est un boson et non un fermion, il n’est donc pas concerné par cette dénomination). Pour le neutrino, on ignore laquelle de ces deux catégories lui convient.
En bombardant des protons à l’aide d’électrons de haute énergie dans un accélérateur de particules, on a pu découvrir que les protons montraient des points durs, et n’étaient pas d’une seule pièce. Cette expérience à mis en lumière l’existence d’un nouveau type de particules, nommées quarks. Un proton en contient trois (les neutrons également). Les quarks sont bien plus petits que le proton. Ce qui fait que le noyau de l’atome est lui-même pratiquement vide, puisque constitué de nucléons vides… A l’heure actuelle, on considère que les quarks sont des particules élémentaires (particules qui n’ont pas de structure).
| Le nom quark a été donné par Murray Gell-Mann, qui les a imaginés, d’après une citation de James Joyce
"Three quarks for Muster Mark !
Finnegans Wake, James Joyce |
Les quarks sont des particules élémentaires massives, qui composent de nombreuses particules. Murray Gell-Mann en a défini les propriétés de telle manière que leurs associations donnent les propriétés observées des particules composées : masse, charge électrique, spin… (si la ville est rose, on peut en déduire que les briques dont elle est construite sont elle-mêmes roses, même si on est trop loin pour les voir). Pour former les protons et neutrons, il a dû considérer qu’il existait deux types de quarks, qu’il a nommés up (u) et down (d), sans quoi protons et neutrons auraient été identiques. Le proton est alors la combinaison de deux quarks up et d’un down (uud), le neutron d’un up et de deux down (udd).
Pour que le spin des protons et neutrons soit 1/2 (ce sont des fermions), il fallait que le spin des quarks soit aussi 1/2. Remarquez que le proton contient deux quarks identiques et un différent. Il suffit que les deux quarks identiques puissent se placer avec leurs spins anti-parallèles (spins +1/2 et -1/2) pour que l’assemblage satisfasse au principe d’exclusion, et obtenir le bon spin.
Pour la charge électrique, il a fallu considérer des charges fractionnaires :
Soit u la charge du quark up, d celle du quark down. La charge du proton sera donc u + u + d = 2u + d. Or la charge du proton vaut +e. Donc on a d’abord : 2u + d = +e.
La charge du neutron est : u + d + d = u + 2d. Mais cette charge est nulle, donc : u + 2d = 0.
On en déduit immédiatement que u = -2d, ce qu’on reporte dans la première équation : 2 (-2d) + d = +e.
-4d + d = -3d = +e.
D’où d = -e / 3. C’est la charge du quark down.
Reportant dans la seconde équation par exemple, il vient : u + 2(-e/3) = 0 ; donc u = 2e / 3. C’est la charge du quark up.
On avait dit que la charge de l’électron était élémentaire, ce qui signifie qu’on ne peut pas la diviser. Si on définit des charges fractionnaires, on se met quelque peu en contradiction. Mais le confinement des quarks lève cette contradiction, puisqu’on ne peut pas observer directement les charges fractionnaires (voir plus bas).
Continuons notre exploration. Dans leurs multiples expériences, les physiciens avaient découvert deux particules, nommées Δ++ et Δ-. Comme leurs noms l’indiquent, la première porte une charge +2e, la seconde une charge -e. Mais leur spin vaut 3/2. Il faut les définir par des quarks. Ceci est facile, et sert de justification à la théorie :
Le Δ++ est constitué de trois quarks u (charge électrique 3 × 2e/3 = 2e), le second est formé de trois quarks d (charge électrique 3 × (-e / 3) = -e).
Toutefois, l’existence de ces deux particules pose un véritable problème : pour obtenir le spin 3/2, il faut considérer que les trois quarks ont leurs spins parallèles (3 fois 1/2 = 3/2). Mais alors, ce sont trois fermions identiques, dans le même état quantique ! En violation apparente avec le principe d’exclusion. Pour sauver la théorie, il faut donc introduire une nouvelle charge, qui sera différente pour les trois quarks. On la nomme charge de couleur, et on lui donne les valeurs rouge, vert et bleu. Ainsi, dans ces particules, les trois quarks doivent obligatoirement être de trois couleurs différentes, et le principe d’exclusion est préservé.
Ceci semble un peu magique, mais la suite des travaux a parfaitement vérifié cette vision des choses, et même étendu la porté de l’explication. C’est la charge de couleur qui rend les quarks sensibles à l’interaction forte.
Ces couleurs n’ont rien à voir avec la notion habituelle, les particules considérées étant bien plus petites que la longueur d’onde de la lumière, mais elles ont été définies par analogie, car leur somme est neutre : bleu + vert + rouge = blanc (ce qui veut dire sans couleur, donc neutre vis-à-vis de l’interaction forte).
Les antiquarks portent des anticouleurs anti-bleu, anti-vert, et anti-rouge. Une couleur et son anti-couleur donnent également du blanc. Comme le + est l’opposé du -, l’anticouleur est l’opposé de la couleur. On pousse parfois l’analogie à l’équivalence anti-bleu = jaune, anti-vert = magenta, et anti-rouge = cyan.
C’est la charge de couleur qui permet l’interaction forte, elle agit sur les quarks et elle est à très courte portée. Puisque les protons et neutrons sont blancs, ils sont neutres vis-à-vis de l’interaction forte, et ne devraient pas y être sensibles… Ils ne devraient pas se coller pour former les noyaux. Mais dans un proton, les trois quarks ne produisent pas une symétrie sphérique : les quarks du proton voisin (ou du neutron), sont plus proches de l’un des trois, et de ce fait la force que celui-ci exerce sur eux est plus importante ; c’est ce résidu d’interaction forte qui produit la force attractive entre protons et neutrons, et assure la cohésion du noyau.
C’est aussi ce résidu qui a été étudié en premier, bien avant de découvrir les quarks. On l’appelle souvent interaction nucléaire, puisqu’elle porte sur les nucléons vus globalement. Le potentiel qui traduit cette action résiduelle, potentiel de Yukawa, a été décrit en 1935 par Yukawa. Il est de la forme :
![]()
C est la constante de couplage de l’interaction. Le terme en r est positif, l’exponentielle aussi, la constante de couplage aussi, donc le signe - placé devant C indique que le potentiel est négatif, et que la force qui en dérive est attractive. m est la masse de la particule qui porte l’interaction.
Quand r = 0, l’exponentielle vaut 1, quelle que soit la masse m. Pour m > 0 et r > 0, l’exposant étant négatif, l’exponentielle tend vers 0 lorsque r croît. Et ce d’autant plus vite que m est plus grande. La valeur de r pour laquelle elle devient négligeable dépend de m, et définit la portée de l’interaction. Au-delà, l’interaction n’agit plus. Si m = 0 (l’exponentielle vaut alors 1), la portée de l’interaction est infinie, et l’on retrouve un potentiel de nature coulombienne (en 1/r). L’exponentielle est donc un terme d’amortissement, qui affaiblit le terme C / r lorsque r augmente.
Pour résumer, nous avons vu que les quarks ont un spin qui vaut 1/2, donc :
D’après la règle énoncée plus haut, un groupement de trois fermions est aussi un fermion. Donc, les nucléons (tois quarks) sont des fermions parce que les quarks en sont !
Le nom de couleur vient des propriétés d’association, qui se résument par :
Ces deux règles permettent d’envisager les compositions possibles. On obtient du blanc par mélange des trois couleurs, donc par association de trois quarks ou de trois antiquarks (qui donneront une anti-particule), mais aussi avec un quark et un antiquark, portant deux couleurs complémentaires : bleu et anti-bleu par exemple.
En dehors de la classification en bosons et fermions, qui est définie par le spin, on utilise une autre classification, définie par la masse. Elle subdivise le même ensemble de particules en :
Ce sont les baryons qui constituent notre matière, la matière baryonique. Lorsqu’on parle de matière non baryonique, on envisage donc l’existence de particules non formées de quarks, mais qui présenteraient une masse, et qui expliqueraient la matière noire.
Les particules constituées de quarks, donc les baryons et les mésons, sont nommées collectivement hadrons (du grec hadros = fort). Comme leur nom l’indique, ce sont celles qui ressentent l’interaction forte, ou interaction de couleur.
| hadrons interaction forte |
baryons part. lourdes |
3 quarks | bleu + vert + rouge |
| anti-bleu + anti-vert + anti-rouge | |||
| mésons part. de masse moyenne |
quark + antiquark | bleu + anti-bleu | |
| vert + anti-vert | |||
| rouge + anti-rouge |
Les quarks qui forment notre matière sont deux : le Up, noté u, et le Down, noté d. Ils se différencient par une nouvelle propriété, un peu analogue au spin, et qu’on a noté isospin. Les valeurs de l’isospin sont haut et bas, d’où les noms des deux quarks.
Le proton est formé de deux quarks up et d’un down (uud), le neutron d’un up et de deux down (udd). Le quark up possède une charge électrique positive +2/3, et le down une charge négative -1/3. Faites le compte : uud, le proton, porte la charge +2/3 +2/3 -1/3 = 3/3 = +1, tandis que udd, le neutron, porte +2/3 -1/3 -1/3 = 0. Le mystère est éclairci.
Le méson π+ (ou pion positif) est ud′ (d′ représente l’anti-quark d). Le quark u porte une charge +2/3, l’anti-d (d′) porte la charge opposée du d, donc +1/3. Le méson π+ porte donc une charge +1, qui justifie son nom. Le méson π- (ou pion négatif), est la combinaison u′d. Sa charge est donc -2/3 (u′) -1/3 (d) = -1. Enfin, il existe un méson neutre. Nommé naturellement π0 , il est de constitution plus complexe : c’est un mélange d’états quantiques, formé de groupements dd′ et uu′. La charge d’un groupe dd′ est -1/3 +1/3 = 0. Pour le groupe uu′, c’est +2/3 - 2/3 = 0. On peut donc, en respectant les règles d’association des états quantiques, former des particules neutres par association de ces groupes uu′ et dd′. Les pions sont produits par les rayons cosmiques.
Toutes les combinaisons précédentes sont bâties sur les quarks de matière normale, u et d. Mais il existe deux autres familles de quarks, les charmé c (charmed) et étrange s (strange), et les top t et bottom b. Ils peuvent également s’associer pour produire des particules complexes, selon les mêmes règles. Et de fait, il y a beaucoup de possibilités… Mais ces groupements permettent de représenter très fidèlement les particules vraiment observées dans les accélérateurs, ce qui valide l’interprétation des quarks. Nous résumerons plus bas leur propriétés.
Prenons comme exemple de particules formées avec ces nouveaux quarks, le méson K+, qui est un assemblage us′, d’un quark up et d’un anti-quark s. Les particules qui contiennent des quarks s ou s′ sont nommées particules étranges.
Tout ce qui précède concerne les particules dans leur état fondamental. Mais il existe aussi des états excités. Par exemple, le proton uud possède normalement un spin 1/2, car deux de ses quarks constituants prennent un état de spin, et le troisième l’état opposé. Mais si on communique à ce proton un peu d’énergie, on peut faire basculer le spin d’un des quarks, et obtenir un assemblage identique, mais de spin 3/2. Cette particule prend le nom de Δ+. C’est en fait un état excité et instable du proton.
Tout ceci peut paraître compliqué, mais en fait, à partir de seulement 6 quarks (et leurs anti-quarks), et quelques règles de construction simples, les physiciens sont parvenus à représenter l’ensemble des particules qu’ils observent dans les accélérateurs, à la fois dans leur état fondamental et dans les états excités. Jusqu’à maintenant, on n’a jamais obtenus de résultats contredisant ce modèle, qui de fait est devenu le modèle standard de la physique des particules.
Confinement des quarks
Les charges fractionnaires définies pour les quarks ne sont jamais observées ! La contradiction évoquée plus haut, relative à la charge élémentaire de l’électron, n’est qu’apparente. Les quarks ne sont jamais observés isolés… Donc, il était impossible d’observer directement une charge fractionnaire. Détaillons ce nouveau problème.
Le potentiel qui agit sur les quarks n’est pas le potentiel de Yukawa, mais il a été déterminé par les résultats des diverses expériences. Il est de la forme :
V(r) = -150 / r + 800 r
Lorsque r est très petit, le second terme est négligeable. Donc, à courte distance, le potentiel se réduit à V(r) = -150 / r. C’est un potentiel coulombien habituel. Mais si r est grand, c’est le premier terme qui devient négligeable. Et le potentiel prend la forme V(r) = 800 r, il est proportionel à la distance. La force, qui dérive (opération mathématique de dérivation) du potentiel, est alors de la forme F = 800. Elle est constante, ne dépend pas de la distance. Quelle que soit la distance qui sépare deux quarks, la force qui les réunit est toujours la même.
Si une fusée s’éloigne de la Terre, à chaque kilomètre parcouru, la force qui la retient diminue. A chaque fois qu’on lui communique un peu d’énergie, elle est un peu plus libre. Pour les quarks, rien de tel. Quelle que soit l’énergie qu’on leur fournisse, ils sont toujours aussi fermement liés l’un à l’autre. Pour les séparer, il faudrait une énergie infinie… On ne peut donc pas les séparer !
Il y a pire : si vous continuez à les éloigner, en fournissant assez d’énergie, vous arriverez à un niveau d’énergie tel que vous pourrez créer une paire quark-antiquark ! Au lieu de séparer les quarks, vous en avez créé deux nouveaux, de même couleur. Au lieu de se séparer, les deux quarks ont formé ainsi un hadron. Impossible donc de les séparer : si on fournit une énergie croissante dans ce but, lorsqu’on atteint l’énergie correspondant à la création d’une paire quark-antiquark, cette paire se crée, diminuant d’autant l’énergie disponible. Si on continue de fournir de l’énergie, on créera ainsi de nouvelles paires, ce qui limite toujours l’énergie disponible, et empêche définitivement de séparer les quarks.
On appelle ce phénomène hadronisation des quarks. Décidément, ce sont de bien étranges particules qui nous constituent !
Dans les accélérateurs de particules, par exemple dans un choc électron-positron, il arrive qu’une paire quark-antiquark soit créée, et que les deux particules s’éloignent dans des directions opposées, à grande vitesse. Entre les deux, la force qui les relie diminue leur énergie, et cette énergie est utilisée pour créer des paires quark-anti-quark. Il se forme ainsi deux jets de hadrons (particules formées avec ces quarks créés), symétriques de part et d’autre du point de choc.
Par contre, si on rapproche des quarks, la force diminue. C’est ce qu’on appelle liberté asymptotique. Dans les conditions qui régnaient après le Big Bang, les quarks étaient très serrés, et donc totalement libres.
Particule d’interaction forte
Les quarks se collent l’un à l’autre par échange de gluons, comme l’interaction électromagnétique se transmet par échange de photons. Mais alors que le photon ne porte pas de charge électrique, chaque gluon porte une charge de couleur, et une charge d’anti-couleur : bleu et anti-rouge par exemple. Ceci devrait faire 9 gluons différents, mais à cause de la neutralité des combinaisons couleur-anticouleur, il n’en existe réellement que 8.
Tous les objets de l’univers s’expliquent par un subtil équilibre entre les distances qui séparent leurs composants, et l’intensité des forces en jeu :
Une bien curieuse affaire a fait courir, au sens propre, les physiciens du début de XXe siècle. Ils ont d’abord découvert qu’un électroscope à feuilles d’or se déchargeait spontanément, sans cause apparente. Il a fallu plus de vingt ans pour résoudre le problème, et c’est Victor Hess qui y est parvenu. Montant en ballon jusqu’à la stratosphère, il a montré que l’électroscope se déchargeait de plus en plus vite avec l’altitude croissante. La décharge venait donc de l’espace, provoquée par un rayonnement alors inconnu. Il a été nommé pour cela rayonnement cosmique. Peu après, on a compris que les rayons cosmiques étaient en fait des particules chargées. Elles avaient les propriétés d’un électron, mais étaient bien plus lourdes. On avait découvert un électron lourd, qui fut nommé muon.
Plus tard, on devait découvrir un troisième électron encore plus lourd, le tau. Ces deux nouvelles particules n’étaient pas connues avant car elles sont instables : il faut les observer très peu de temps après leur formation, avant leur désintégration. Les rayons cosmiques primaires arrivant sur la haute atmosphère, produisent des muons qu’on capte au sol. Le muon se désintègre en 2,2 µs en un électron, et deux neutrinos, à cause de sa masse supérieure.
On a ensuite compris que, dans la désintégration béta, le neutrino est associé à l’électron. Si bien qu’il devenait évident que d’autres neutrinos, associés respectivement au muon et au tau, devaient aussi exister. On n’a pas tardé à les mettre en évidence. Il a fallu donner des noms distinctifs à ces trois particules. Le premier neutrino a pris le nom de neutrino électronique, les deux autres étant le neutrino muonique et le neutrino tauique.
Les neutrinos ont une masse très faible, et pendant longtemps on a considéré qu’elle était nulle. Mais il n’en est rien, et c’est la physique du Soleil qui en a apporté l’indication sinon la preuve. Mais cette masse est vraiment extrêmement faible.
Les trois électrons, et les trois neutrinos, sont tous de faible masse. Aussi, ils sont nommés collectivement leptons, ce qui signifie léger en grec.
En utilisant de nouveaux outils, on fait toujours des découvertes innattendues. La Nature est plus riche que notre imagination… C’est ainsi que dans les accélérateurs de particules, construits pour étudier la matière courante, on a découvert des particules nouvelles, tout à fait surprenantes. Nous avons déjà parlé du muon et du tau, découverts dans l’accélérateur de particules naturel qu’est le cosmos. Mais les physiciens ont observé dans leurs détecteurs la signature de particules ressemblant aux quarks, mais tout de même différentes. Ils ont montré que ce sont des quarks, mais se différentiaient entre eux par une nouvelle propriété, qu’ils ont nommé saveur (encore un terme bien curieux, puisque la véritable saveur provient de la chimie, qui se passe à des dimensions des milliards de fois plus grandes).
Mais ces quarks nouveaux possèdent aussi l’isospin, et sont donc arrivés par paires. Les deux quarks déjà connus ont pour saveur up et down. Les nouveaux sont les quarks charmé c (vous avez bien lu, en anglais charmed), étrange s (strange), vérité t (truth, mais on préfère une autre apellation qui commence aussi par t : top), et le dernier beauté b (beauté n’est pas utilisé, on lui préfère bottom, dont la signification anglaise est tout de même moins poétique).
Maintenant, toutes les particules élémentaires qui composent la matière ont été décrites. Elles se classent en trois familles, qui possèdent des propriétés très semblables.
La première famille est celle de la matière que nous connaissons, les autres sont plus exotiques. Chaque famille comprend deux quarks, et deux leptons. Les particules des deux dernières familles sont instables, et se désintègrent rapidement en particules équivalentes de la première.
Le tableau ci-dessous les résume :

Ce sont les particules qu’on considère aujourd’hui comme élémentaires, en ce sens que les accélérateurs de particules n’ont jamais permis de les casser en constituants plus petits. Leurs masses sont indiquées entre parenthèses (en omettant / c2). Les quarks sont les briques qui servent à construire la matière ordinaire. Les leptons sont les constituants légers de celle-ci. Les antiparticules ne sont pas notées.
De même, on peut écrire le tableau qui résume les propriétés essentielles des quatre forces fondamentales, et des particules associées :
| interraction | découvreur | médiateur | masse | spin | charge | vie | agit sur | portée | intensité |
|---|---|---|---|---|---|---|---|---|---|
| forte | Hideki Yukawa | gluons | 0 | 1 | 0 | ∞ | quarks | 1,5 fermi | 1 |
| électromagnétique | Maxwell | photon | 0 | 1 | 0 | ∞ | quarks, leptons | infinie | 10-2 |
| faible | Glashow, S. Weinberg, A. Salam | W+ | 80,4 GeV | 1 | +e | 3 10-25 s | quarks, leptons | 1,5 fermi | 10-7 |
| W- | 80,4 GeV | 1 | -e | 3 10-25 s | |||||
| Z0 | 91,2 GeV | 1 | 0 | 3 10-25 s | |||||
| gravitation | Einstein | graviton | 0 | 2 | 0 | ∞ | quarks, leptons | infinie | 10-36 |
Le nom du boson W vient de l’anglais Weak (faible). Les masses sont données en GeV ; il faut lire GeV/c2 (voir plus haut).
L’intensité est une indication de la puissance relative des interactions. En fait, l’intensité de l’interaction forte dépend de l’énergie mise en jeu, ce qui explique que l’on trouve des valeurs différentes selon les auteurs. Lorsque l’énergie est très élevée, l’interaction forte diminue, jusqu’à une intensité égale à celle de l’interaction faible. Cette convergence des intensités est à la base des tentatives d’unification des forces fondamentales : les physiciens rêvent d’une seule force, qui expliquerait l’Univers lorsqu’il était très chaud, à très haute énergie.
On remarque sur ce tableau que l’interaction gravitationnelle est de très, très loin, la plus faible. Mais sa portée est infinie, aussi les petites contributions de chaque particule s’ajoutent pour arriver à une force colossale. Les particules médiatrices de l’interaction électromagnétique et de la gravitation ont une masse nulle, conférant à ces interactions une portée infinie. A l’opposé, la masse des bosons faibles (W+, W- et Z0) est très élevée, impliquant une très faible portée de l’interaction faible.
L’interaction forte a été découverte comme force unissant les nucléons, et assurant la stabilité du noyau atomique. Mais ses propriétés sont quelque peu curieuses. Et lorsqu’on a mis en évidence les quarks, constituants des nucléons, la question s’est posée : qu’est-ce qui réunit les quark ? Il faut une force, et l’interaction forte est la candidate naturelle. On doit alors considérer que le nucléon est formé de trois quarks, liés les uns aux autres par l’interaction forte, et donc que cette dernière n’agit pas sur les nucléons, mais sur leurs composants.
La particule d’interaction, le gluon, a une masse nulle. Donc, la portée de l’interaction est infinie. Pourtant, la force qui unit les nucléons est au contraire à très courte portée… Comment concilier ces deux constatations opposées ?
Le cas de l’interaction forte est plus complexe que celui des autres interactions. Les particules de matière sensibles à l’interaction forte, les quarks, ne peuvent apparaître isolés : ils ne se montrent que dans des combinaisons blanches (neutres). Considérons un quark. Il crée autour de lui un champ de couleur (d’interaction forte) qui possède la symétrie sphérique. Plaçons deux autres quarks à proximité, tels que les trois couleurs soient différentes (la particule formée ne peut exister que si elle est blanche). Leurs champs sphériques se mélangent, et forment un champ résultant complexe. Si on s’éloigne suffisamment de l’ensemble, la séparation entre les trois quarks devient négligeable devant la distance d’observation, et ils apparaissent comme une unique particule blanche (neutre), donc le champ global produit est nul. C’est pourquoi le champ de couleur voit sa portée limitée par l’association neutre des quarks, à une distance de l’ordre du diamètre d’un noyau atomique.
Par contre, pour un quark qui se trouve pratiquement au contact avec le proton, le champ produit par ce dernier apparaît non symétrique : le quark extérieur ne peut pas être à la même distance des trois quarks qui le composent, et donc ressent plus l’un que l’autre. C’est ce reste d’interaction forte qui lie protons et neutrons dans le noyau atomique.
Il y a une analogie importante avec l’interaction électromagnétique. Une molécule est globalement neutre, mais son nuage électronique n’a pas forcément la symétrie sphérique. C’est le cas des molécules polaires : les électrons sont plus nombreux d’un côté que de l’autre. Alors, cette molécule crée autour d’elle un potentiel qui lui permet de se lier faiblement à un atome ou une autre molécule. Cette force de liaison est nommée force de van der Wals.
Jusqu’ici, nous avons évoqué les baryons (trois quarks), mais pas les mésons. La raison en est que ces derniers ne constituent pas de manière durable la matière habituelle. Ces particules n’existent que brièvement à la suite de certaines interactions qui les produisent. Elles apparaissent par exemple dans l’interaction des rayons cosmiques avec la haute atmosphère terrestre.
La première que nous mentionnerons est le méson K, ou kaon. Il est constitué d’une paire quark-antiquark (puisque c’est un méson). Il reste à préciser de quel quark et de quel antiquark il est fait. En fait, il existe plusieurs kaons : l’un est positif, un autre négatif, mais il en existe encore deux autres plus difficiles à interpréter. Il est temps de décrire ici un phénomène curieux de la Mécanique Quantique : la superposition d’états.
Cette notion est délicate, car elle ne se produit pas dans la vie courante. Une particule, à cause du principe d’incertitude d’Heisenberg, ne peut pas être caractérisée individuellement avec une précision fixée. Si on connait sa position par exemple, on ne pourra pas connaître sa vitesse. Alors, considérant un ensemble de particules identiques, on peut dire par exemple dans l’expérience des trous de Young vue plus haut, que 50 % des électrons passent par le trou 1, et 50 % par le trou 2. Ce qu’on résume en disant que l’électron moyen passe par 50 % du trou 1 et 50 % du trou 2… Autrement dit, l’électron est un mélange des deux états possibles. Pour un électron donné, il est bien évident qu’une des possibilités seulement se réalise. Mais comme on ignore laquelle, on ne peut parler que de statistiques, ce que fait le mélange d’états.
Pour en revenir aux kaons, il en existe deux autres qui sont des mélanges d’états :
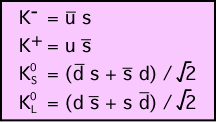
Le premier associe un antiquark up, de charge électrique -2/3 (moins parce que c’est un anti-quark), à un quark strange, de charge -1/3. Le résultat est une particule de charge -1, ce qui justifie le signe - accolé au nom de la particule.
Le second associe un quark up, de charge +2/3, à un antiquark strange, de charge +1/3, et donne une particule de charge +1.
Le troisième est une composition de deux états. Le premier de ces état à la charge +1/3 + (-1/3) = 0, le second état à la charge +1/3 + (-1/3) = 0. La somme des deux états est donc nulle, d’où l’exposant 0 accolé au nom de la particule.
Enfin, le dernier possède une charge nulle également, puisque ((-1/3) + (+1/3)) + ((-1/3) + (+1/3)) = 0.
Le noyau atomique étant constitué de plusieurs particules, se pose le problème de leur arrangement interne. Comment les nucléons se comportent-ils dans le noyau ? Sont-ils statiques, fixés une fois pour toutes ? Sont-ils mobiles ? Sont-ils entassés n’importe comment ou bien arrangés selon une loi à découvrir ? C’est le genre de question qui s’est posée après la découverte du neutron, et qui se pose encore d’ailleurs, car la solution correcte n’est peut-être pas encore trouvée.
Tout d’abord, il faut parler d’une propriété des noyaux atomiques pris globalement. Certains sont stables, d’autres instables, et les physiciens ont vite fait le tri entre eux. Ce faisant, ils ont remarqué que certains numéros atomiques (nombre de protons) donnaient des noyaux plus stables que d’autres. Il en est de même avec les neutrons. Les nombres de protons ou neutrons suivants sont dit magiques : 2, 8, 20, 28, 50, 82, 126. Les noyaux qui possèdent l’un de ces nombres de protons ou neutrons sont particulièrement stables. Le plomb 208 en est un : il comporte 82 protons, et donc 208 - 82 = 126 neutrons. Ses deux nombres sont magiques. Un modèle de noyau doit expliquer les nombres magiques, et les déterminer par la théorie. Le noyau d’hélium 4 est doublement magique, puisqu’il l’est pour ses protons (2) et pour ses neutrons (2).
Un premier modèle est celui de la goutte liquide : les nucléons sont relativement libres dans le noyau, comme les molécules dans un liquide. Ce modèle, correctement établi, a connu certains succès, et explique certaines des propriétés du noyau. Mais pas toutes, et il présente des défauts. Le plus grave est qu’il n’est pas quantique, et ne permet pas d’expliquer certains états excités discrets. Il est donc abandonné.
Le second modèle reprend pour le noyau une structure semblable à celle du cortège électronique : c’est le modèle en couches. Comme les électrons se placent dans des niveaux d’énergie discrets autour du noyau, les nucléons se placent de même à l’intérieur du noyau. Ces couches nucléoniques correspondent aux nombres magiques. Les noyaux correspondant à un nombre magique de protons ont la dernière couche complète : par analogie avec les couches électroniques, ce sont les plus stables.
Entre deux niveaux d’énergie électroniques, il y a une différence d’énergie qui est de l’ordre de grandeur de quelques électrons-volt. Les photons émis par une transition sont compris entre l’infrarouge et l’ultraviolet. Par contre, entre deux niveaux nucléoniques, la différence d’énergie est de l’ordre de 100 keV, ce qui fait que les photons émis par désexcitation nucléaire sont dans le domaine gamma très énergétique.
Le modèle en couches est très important, car il explique assez naturellement les réactions résonnantes, qui permettent par exemple la fusion de l’hélium dans les géantes rouges.
Physique fondamentale et astronomie ont développé, au XXe siècle, la connaissance de la matière, à petite et grande échelle. La matière habituelle… D’autres particules ont fait plus tard leur apparition sur la scène scientifique. La Physique des particules doit rendre compte de leur existence et de leurs propriétés.
A l’échelle des particules, règne la Mécanique Quantique. Impossible de s’en passer. Il faut donc une théorie qui satisfasse aux deux principes fondamentaux, le principe d’incertitude, et le principe d’exclusion.
Le Modèle Standard des particules (les deux tableaux vus plus haut en décrivent les particules et leurs propriétés), a été établi, et donne des résultats excellents. Il décrit les interactions électromagnétique, forte et faible. Il est quantique, et compatible avec la relativité. On pourrait donc s’en contenter, mais le conditionnel montre bien qu’il y a une difficulté. Celle-ci tient en grande partie dans le problème de la masse. Si vous reprennez les deux tableaux, vous verrez des valeurs de masse affectées à chaque particule, mais vous ne trouverez dans le texte aucune explication à leur sujet. Les masses sont des paramètres libres, qui doivent être obtenues par l’observation (et qui le sont effectivement). Le Modèle Standard contient en tout 29 paramètres libres, ce qui est énorme.
Une théorie dans laquelle il y a tant de paramètres libres est suspecte : on suppose qu’il y a des relations non encore découvertes qui lieraient ces paramètres, et permettraient de les réduire à un nombre bien plus petit. Beaucoup de chercheurs travaillent donc dans cette direction, sur le plan théorique. Ainsi, dans la théorie la plus avancée, on a imaginé un mécanisme, dit mécanisme de Higgs, qui donnerait aux particules leur masse, et nous fournirait une explication plausible de leur existence. Si ce mécanisme de Higgs a lieu, alors il y a un champ de Higgs et un boson associé, le boson de Higgs. La chasse au boson de Higgs est donc ouverte.
Le LEP (Large Electron-Positron collider), qui était situé en souterrain à la frontière franco-suisse près de Genève, et qui était le plus puissant accélérateur de particules, a donné un résultat qui peut s’interpréter comme une confirmation du boson de Higgs. Mais il a été démantelé… pour faire place au LHC (Large Hadron Collider) dans le même tunnel. Le LHC a été construit en grande partie dans le but de trouver ce boson de Higgs, ou de démontrer qu’il n’existe pas. Donc de confirmer ou d’infirmer la théorie qui prévoit son existence.
La Mécanique Quantique, outil indispensable pour cette physique, nous propose des équations très complexes, qu’il est impossible de résoudre analytiquement. Ceci ne doit pas étonner, sachant que le mouvement des trois corps en mécanique céleste, bien plus simple, n’a pas lui-même de solution analytique. La mécanique céleste a contourné le problème en introduisant le calcul des perturbations : si le problème se décompose en une force principale, dominante, et une force secondaire dite perturbation, alors on peut développer les équations en séries, calculables. Mais dans le cas de trois corps de masses semblables, cette méthode ne s’applique évidemment pas, et seul un calcul pas à pas permet de déterminer une solution numérique. En Mécanique Quantique, on s’adresse à des particules ayant souvent des masses semblables, et donc on est dans le plus mauvais cas de figure.
Une question simple se pose : peut-on calculer la masse du proton, ou celle du neutron, à partir des masses des quarks qui les constituent ? La réponse est non, aujourd’hui. En effet, pour calculer la masse du proton, il faut résoudre les équations décrivant les interactions entre les trois quarks. Ceux-ci sont de masses égales… Les calculs que l’on peut faire aujourd’hui sont trop approximatifs. La théorie des perturbations s’applique dans un grand domaine d’énergies élevées, et donne de très bons résultats. Mais lorsque l’énergie tombe au niveau de celle du proton, l’approximation des perturbations devient bien trop mauvaise pour donner un résultat acceptable. Il faudra trouver une méthode bien plus directe, et ce problème est l’un des sept problèmes ouverts pour la résolution desquels l’Institut Clay a proposé en 2000 un prix d’un million de dollars…
L’idéal des physiciens serait de trouver un tout petit nombre de particules, dites élémentaires, qui se combineraient pour former toutes les autres. Et effectivement, on connaît quelques particules que l’on n’a jamais réussi à casser (elles sont donc élémentaires, sans structure, jusqu’à preuve du contraire), et d’autres qu’on a pu briser en divers composants. Malheureusement pour l’idéal, le zoo des particules est bien plus riche qu’on ne l’espérait. Plus on augmente l’énergie des accélérateurs, avec l’espoir de briser des particules pour les analyser, plus on crée de nouvelles particules par transformation de l’énergie. Chaque nouvelle particule pose un problème supplémentaire.
Δ++ uuu (charge 3 × 2/3 = +2) , Δ+ uud (charge 2 × 2/3 - 1/3 = +1), Δ0 udd (charge 2/3 - 2 × 1/3 = 0), Δ- ddd (charge 3 × (-1/3) = -1). On remarque que Δ+ et Δ0 sont exactement de même composition que les nucléons : proton uud et neutron udd. Pourtant, ce sont des particules différentes, si on considère le spin des quarks. Dans le proton et le neutron, deux des quarks ont le spin dans une direction, et le troisième dans la direction opposée. De ce fait, le spin des nucléons est 1/2. Dans les particules Δ, les spins sont tous alignés, et donc le spin vaut 3/2. Ayant la même composition que les nucléons, les Δ0 et Δ+ sont donc considérés comme des états excités de ces nucléons.
Les Δ ont leurs antiparticules, formées avec les antiquarks correspondants. Leur masse est 1,232 GeV/c2.
Les particules Ω constituent toute une famille dont seulement deux membres ont été observés. Ces particules ne contiennent ni quark u ni d, mais tous les autres sont possibles, ce qui fait un nombre de combinaisons important :
| nom | composition | charge | spin | étrangeté | charme | bottomness | observé |
|---|---|---|---|---|---|---|---|
| Ω- | sss | -1 | 3/2 | -3 | 0 | 0 | oui |
| Ω-b | ssb | -1 | 1/2 | -2 | 0 | -1 | |
| Ω0c | ssc | 0 | 1/2 | -2 | +1 | 0 | oui |
| Ω-bb | sbb | -1 | 1/2 | -1 | 0 | -2 | |
| Ω0cb | sbc | 0 | 1/2 | -1 | +1 | -1 | |
| Ω+cc | scc | +1 | 1/2 | -1 | +2 | 0 | |
| Ω-bbb | bbb | -1 | 3/2 | 0 | 0 | -3 | |
| Ω++ccc | ccc | +2 | 3/2 | 0 | +3 | 0 | |
| Ω+ccb | bcc | +1 | 1/2 | 0 | +2 | -1 | |
| Ω0cbb | bbc | 0 | 1/2 | 0 | +1 | -2 |
Toutes ces particules ont leur antiparticule, dans laquelle les quarks sont remplacés par les antiquarks correspondants. Le passage des quarks aux antiquarks changeant le signe de la charge électrique, il en est de même pour les anti Omégas par rapport aux Omégas.
Passons maintenant aux combinaisons quark-antiquark, que l’on nomme de manière générique quarkonium. Lorsqu’on associe un quark et un antiquark, on obtient une particule qui peut être dans son état fondamental d’énergie minimale, ou dans un état excité. Les états excités ayant une énergie supérieure ont aussi une masse plus élevée (E = mc2), et sont instables. Mais ces états apparaissent souvent dans les expériences en accélérateur. Ce sont parfois eux qui ont été détectés les premiers, éventuellement les seuls.
Considérons d’abord la configuration obtenue avec quark et antiquark b&,nsp;: bb′. Cette configuration est nommée bottomium (quarkonium bottom), pour son état fondamental. Le bottomium a été découvert par les différents états du méson &upsih.
La seconde configuration de quarkonium est obtenue avec quark et antiquark charmés c : cc′. Elle est nommée charmonium. Le J/Ψ est de composition cc′, c’est donc un état excité du charmonium dont la masse 3,096 GeV/c2 est un peu supérieure à celle de l’état fondamental. La masse étant supérieure, cette particule est instable et se désintègre en un peu moins de 10-20 s.
Le nom curieux du J/Ψ est historique : il a été découvert simultanément (les deux publications datées du 11 novembre 1974) par deux équipes, qui bien sûr lui ont donné des noms différents. Du fait de la simultanéité des découvertes, on a associé les deux noms sous cette forme exceptionnelle.
Les physiciens bâtissent des théories pour expliquer tout ce qu’ils ont trouvé. Malheureusement, ces théories, pour être cohérentes, prévoient l’existence de particules non encore observées… qu’il faut chercher à leur tour, pour valider ou invalider la théorie ! Les choses ne sont pas simples.
Comment décrit-on une particule ? Par son état quantique, qui est l’énoncé de quelques propriétés.
La physique des particules a pour objet de décrire les particules qui existent, et leurs propriétés, et surtout d’expliquer comment elles se transforment, avec quelle probabilité, quelle énergie…
Il existe d’autres combinaisons plus lourdes, nommées hypérons. Les baryons sont donc l’ensemble des nucléons et des hypérons (les hypérons n’apparaissent pas dans le tableau).
| particule | masse MeV/c2 | particule | masse MeV/c2 |
|---|---|---|---|
| e | 0,510999 | neutron | 939,6 |
| μ | 105,658 | proton | 938,3 |
| τ | 1776,99 | π+, π- | 139,57 |
| u | 1,5 à 3,0 MeV/c2 | π0 | 134, 976 |
| d | 3 à 7 | K+, K- | 493,677 |
| s | 70 à 120 | K0 | 497,648 |
| c | 1,25 | γ (photon) | < 6 10-17 eV |
| b | 4,2 | g (gluon) | 0 |
| t | 174,2 | W+, W- | 80,403 103 |
| H0 Higgs | > 114,4 103 | Z0 | 91,1876 103 |
A gauche, les particules élémentaires, leptons et quarks, et hypothétique boson de Higgs. A droite, les particules composites, hadrons d’abord, et bosons d’interaction ensuite. Les masses sont données en équivalent énergie (Mev/c2), sauf pour le photon, dont la masse est extrêmement petite, et peut-être strictement nulle.
Les incertitudes ne sont pas mentionnées, ce tableau étant donné seulement pour mémoire. Les données sont extraites du Particle Physics Booklet publié par le CERN, édition 2006.
Après le grand succès de Maxwell, qui a unifié deux interactions autrefois distinctes (électricité et magnétisme), la grande quête est celle d’une interaction unique, qui engloberait toutes celles que l’on connait. Dans les conditions normales que nous connaissons, électricité et magnétisme sont de même intensité. C’est ce qui a permi à Maxwell de réussir son travail. Mais les autres interactions ont des intensités très différentes, ce qui fait qu’a priori elles apparaissent très dissemblables.
Signalons à ce sujet que l’électromagnétisme de Maxwell contient les bases de la Relativité : on montre que la théorie implique l’existence d’ondes qui se propagent à la vitesse c :
![]()
où ε0 et μ0 sont des constantes. Il s’ensuit que c est également une constante. C’est la vitesse de la lumière, qui ne dépend donc pas de l’observateur.
L’électrodynamique quantique (Quantum ElectroDynamics, QED) est la théorie quantique de l’électromagnétisme. Elle n’unifie pas deux interactions différentes, mais quantifie l’électromagnétisme. Elle a remporté de grands succès, comme l’explication d’un dédoublement des raies spectrales de l’hydrogène, produit par les fluctuations du vide (décalage Lamb).
Tomonaga, Schwinger et Feynman ont eu le prix Nobel de physique 1965 pour cette théorie.
La théorie de l’interaction faible a été établie par Enrico Fermi. Mais elle s’appuie sur des expériences faites à énergie assez basse, celle disponible dans les accélérateurs de l’époque. Aussi, si on l’utilise dans une gamme d’énergie élevée, n’est-elle plus tout à fait en accord avec les observations. L’interaction faible voit en effet son intensité augmenter avec les énergies croissantes. Tellement que, vers les 100 GeV, elle devient équivalente à l’interaction électromagnétique. C’est ce qui justifie leur unification. C’est la masse des bosons W± et du Z0 qui limite la portée de l’interaction faible, alors que la masse nulle du photon autorise une portée infine pour l’électromagnétisme.
La première unification est la théorie électrofaible. Comme son nom l’indique, elle unifie l’interaction électromagnétique avec l’interaction faible.
Cette théorie électrofaible a valu le prix Nobel de physique à S. Glashow, A. Salam et S. Weinberg en 1979.
La théorie qui explique la constitution de certaines particules en quarks est la chromodynamique quantique (ce qui rappelle qu’elle décrit l’interaction de couleur, ou interaction forte). Elle a été établie par David Politzer, Frank Wilczek et David Gross en 1973, et leur a valu le prix Nobel de physique en 2004.
Les équations qui décrivent un système physique sont invariantes par une certaine transformation (symétrie) ; mais les solutions de cette équation peuvent être symétriques dans un domaine, et non dans un autre.
Une barre d’acier verticale, sur laquelle on applique un poids bien centré, se tasse si le poids n’est pas trop grand. L’ensemble est symétrique par rapport à l’axe de la barre. Si le poids est trop grand, la barre se plie dans une direction aléatoire. Il y a alors brisure de symétrie.
Un exemple courant de brisure de symétrie est le gel de l’eau. Lorsque la surface d’un lac gèle en hiver, elle passe de l’état liquide à l’état solide. Cette transition de phase (de la phase liquide vers la phase solide), s’accompagne d’un réarrangement des molécules d’eau. Dans la phase liquide, les molécules d’eau sont orientées dans n’importe quelle direction, car elles possèdent suffisamment d’énergie pour s’agiter et tourner, présentant successivement toutes les orientations possibles. Les chocs qu’elles reçoivent des autres molécules changent de même leur orientation. Toutes les directions de l’espace sont alors représentées par un ensemble de molécules à chaque instant. Mais lorsque l’eau commence à geler, l’agitation des molécules diminue fortement, et elles ont tendance à s’orienter toutes dans une même direction, car cet arragement minimise l’énergie de l’ensemble. C’est cette orientation commune qui construit le cristal (la forme des flocons de neige par exemple). Alors que dans l’état liquide les molécules ont toutes les orientations possibles, donc que le liquide présente le même aspect dans toutes les directions, une fois gélée, l’eau a perdu cette symétrie. L’orientation commune de toutes les molécules désigne une direction particulière de l’espace comme privilégiée. On dit qu’il y a eu une brisure de symétrie. Bien entendu, l’orientation des molécules d’eau se fait de proche en proche, à partir d’un germe où le gel commence. Ce germe donne le ton, d’une certaine manière, en imposant son orientation aux molécules voisines, qui à leur tour vont l’imposer à leur voisines. Ainsi, de proche en proche, cette orientation aléatoire de la première molécule va se répandre à toutes les molécules alentour.
Cet exemple vous montre aussi que la brisure de symétrie est liée à une baisse de température, c’est-à-dire d’énergie. Et elle caractérise une transition de phase. En cosmologie, on trouve ainsi plusieurs transitions de phase, qui participent à décrire l’état de l’Univers aujourd’hui, à partir d’un état extrêmement chaud initial.
Attention, l’exemple du lac peut s’étendre encore un peu : lorsque le gel commence, il n’y a aucune raison que ce soit un un seul point. Plusieurs germes peuvent commencer le gel en des endroits différents, et c’est bien ce qu’il se passe. Mais puisque l’orientation de la molécule germe est aléatoire, deux germes différents ne seront sûrement pas orientés pareillement. Et lorsque le gel se propage, il va produire des plaques qui s’étendent, avec des orientations différentes. Et lorsque deux plaques se rejoignent, on va constater un défaut d’orientation à leur jonction : une molécule d’eau à la jonction ne peut prendre deux orientation différentes. Elle doit choisir l’une ou l’autre, et par conséquent on observera deux molécules voisines d’orientation discordantes. Ces défauts dans le cristal sont nommés défaut topologiques. On les observe dans les cristaux, où la cristallisation se fait aussi à partir de germes. Et on envisage qu’ils aient pu apparaître dans le tissus même de l’Univers dans sa prime jeunesse, et ceci pose en cosmologie des problèmes actuellement non résolus.
On trouve des cas de brisure de symétrie dans la physique des particules. En particulier, le mécanisme de Higgs expliquerait la masse des particules par ce phénomène.
La supersymétrie consiste à unifier la matière et les forces, c’est-à-dire les fermions et les bosons. Pour cela, il est nécessaire que toute particule ait son superpartenaire. Le quark est associé à un quark supersymétrique, l’électron à un électron supersymétrique… De plus, le superpartenaire d’un boson est un fermion et réciproquement. Pour trouver des noms parlants pour ces nouvelles particules, on a pris la convention de placer un "s" devant le nom d’un fermion, pour en faire le boson superpartenaire. Ainsi, le superpartenaire de l’électron (un fermion), est le sélectron (un boson). Et pour les bosons, on a décidé d’ajouter le suffixe "ino" au nom du boson. Ainsi, le photino (fermion) est le superpartenaire du photon (boson). La supersymétrie multiplie par deux le nombre de particules (et même plus…). L’unification a un prix !
Mais les physiciens ne perdent pas leur humour :
«… Une paire (de particules supersymétriques) suivant une autre, tout cela se rassemblait en une véritable arche de Noé des particules. Tôt ou tard, pris au filet des nouveaux snoms et nominos, vous commencez à vous sentir comme Sbozo le clown. Ou Bozo le clownino. N’importino squoi… »
Lee Smolin
Rien ne va plus en physique
Pour fixer les idées, voici un tableau établissant un parallèle entre les particules normales et les nouvelles particules supersymétriques :
| particule normale | symbole | spin | particule nouvelle | symbole | spin |
|---|---|---|---|---|---|
| électron | e | 1/2 | sélectron | ẽ | 0 |
| muon | μ | 1/2 | smuon | 0 | |
| tau | τ | 1/2 | stau | 0 | |
| neutrino | ν | 1/2 | sneutrino | 0 | |
| quark | q | 1/2 | squark | 0 | |
| photon | γ | 1 | photino | 1/2 | |
| bosons W | W+, W- | 1 | Wino | ~W | 1/2 |
| boson Z | Z0 | 1 | Zino | ~Z | 1/2 |
| gluons | g | 1 | gluino | ~g | 3/2 |
| graviton | G | 2 | gravitino | ~G | 3/2 |
| boson de Higgs | h | 0 | Higgsino | ~h | 1/2 |
Toutes les théories des particules élémentaires considèrent en fait que les particules sont ponctuelles, sans dimension. Et certains problèmes se posent, qui viennent de là. Alors, certains ont imaginé de décrire les particules non plus comme des points, mais comme de minuscules (oh, combien !) cordes ayant une dimension. Ces cordes vibrent, un peu comme une corde de guitare. Etant finies, elles ont des modes de vibration bien définis, qui correspondent aux états excités de la particule.
Dans une théorie des cordes, les cordes peuvent vibrer dans bien plus que 3 dimensions. Mais comme nous n’en connaissons que trois, il faut que les autres soient invisibles, donc trop petites pour être perçues. On considère qu’elles sont enroulées sur elle-mêmes, mais ceci est difficile à imaginer…
Il n’y a pas une théorie des cordes, mais plusieurs, certains prétendent qu’il y en a une infinité… En fait, ces théories s’appuient sur des paramètres ajustables, et de là vient la difficulté. On règle les paramètres pour que la théorie s’adapte aux observations. Ce qui veut dire qu’on peut adapter la théorie à un peu n’importe quoi : elle n’est pas réfutable, ce qui la rend totalement inacceptable pour beaucoup de physiciens.
| particule | origine | étymologie | explication |
|---|---|---|---|
| atome | grecque | a = privatif; tomein = couper | insécable, qui est réputé non divisible en éléments plus petits. |
| lepton | grecque | leptos = léger | les leptons sont les particules légères, électron, muon, tau et les neutrinos. |
| hadron | grecque | hadros = fort | les hadrons sont les particules sensibles à l’interaction forte. |
| baryon | grecque | barys = lourd | les baryons sont les particules lourdes, proton, neutron, etc. |
| méson | grecque | mésos = moyen, intermédiaire | les mésons sont les particules de masse intermédiaire ; ce sont des bosons formés d’un quark et d’un anti-quark. |
| boson | nom propre | Bose, physicien indien | les bosons sont les particules qui se placent de préférence toutes dans le même état quantique. Ce sont les particules d’interaction. |
| fermion | nom propre | Fermi, physicien italien | les fermions sont les particules qui se placent dans des états quantiques différents. Ce sont les particules de matière. |
| boson W boson Z0 |
anglaise | weak = faible | les bosons W + et - sont les deux vecteurs chargés de l’interaction faible. Le dernier est neutre, c’est le Z0. |
---=OO=---