Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Loi de la Gravitation Universelle | |||||||
Ce petit chapitre décrit (à peu de choses près) comment Newton a découvert la loi de la Gravitation Universelle.
Avant lui, Galilée avait découvert la loi de l’inertie :
un objet, non soumis à des forces extérieures, reste au repos, ou conserve un mouvement rectiligne uniforme.
Cette loi est une abstraction pure, car il est impossible d’en réunir les conditions à la surface de la Terre, puisqu’on est toujours soumis à une force extérieure : la gravité. Mais le champ de gravitation, dans l’espace restreint du laboratoire, est très uniforme, donc son action est la même partout. Et de plus, Galilée a utilisé des plans horizontaux très lisses, sur lesquels les frottements sont très faibles : il a extrapolé sur des frottements nuls.
Ensuite, Kepler a énoncé les lois du mouvement des planètes, dans ses fameuses 3 lois :
Enfin, Newton lui-même a fondé la dynamique en énonçant les lois :
Partant de la loi de l’inertie de Galilée et de sa seconde loi, Newton a retrouvé la loi des aires de Kepler. Voici la démonstration :
Considérons le Soleil, et une planète placée en A, et se dirigeant vers B. On suppose que le Soleil n’exerce aucune force sur la planète. On considère le point B’, aligné avec A et B, et tel que BB’ = AB. D’après la loi de l’inertie, la planète conservera son mouvement rectiligne uniforme, et donc elle mettra le même temps pour aller de A à B et de B à B’.
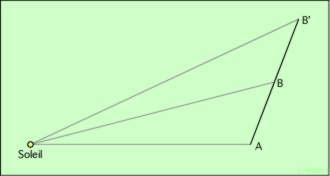
On vérifie que les triangles SAB et SBB’ ont des surfaces égales :
Prenons AB et BB’ comme bases de ces deux triangles. La surface d’un triangle vaut 1/2 b h, où b est la base, et h la hauteur. Ici, les deux bases AB et BB’sont égales. Et les deux hauteurs sont confondues :
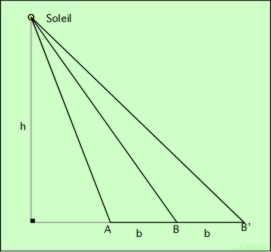
Les deux triangles ayant des bases égales, et la même hauteur, ont des aires égales.
Maintenant, ajoutons la force exercée par le Soleil, et dirigée vers lui. Elle est portée par le segment BK (figure ci-dessous). Si le temps considéré est bref, on peut décomposer le mouvement réel de la planète en supposant qu’elle va de B à B’, puis de B’ à C. Pour calculer chacun de ces déplacements, il faut considérer le même temps t, puisqu’en fait ils sont simultanés.
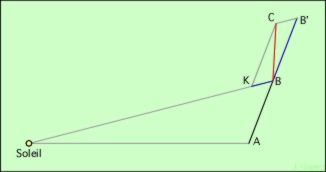
Le premier de ces déplacements, de B à B’, est fait sous l’action de l’inertie seule, aucune force n’intervenant (l’action de la force est reportée sur la seconde partie du mouvement). Il est donc dans le prolongement de AB, et son amplitude est simplement égale à AB par définition.
Pour la seconde partie de la décomposition, les choses sont un peu plus compliquées. La force appliquée en B aurait amené la planète en K (en l’absence d’inertie, comme nous avons considéré l’absence de force dans la première partie). Si on applique la force en B’, le calcul semble être différent, en particulier la direction de la force n’est pas la même. Il faut imaginer le triangle SAB infiniment plat, avec un angle en S infiniment petit. Alors, on peut considérer que la force appliquée en B, d’amplitude BK, s’applique à l’identique en B’, B’ étant infiniment voisin de B. On dessine donc sur la figure un segment B’C, parallèle à BK, et de même longueur. C’est lui qui définit le chemin que suit la planète, à partir de B, sous l’action de la force. Ces deux parcours infinitésimaux BB’ et B’C sont des vecteurs. Ils se composent pour donner comme somme la diagonale du parallélogramme, chemin qui sera réellement parcouru par la planète.
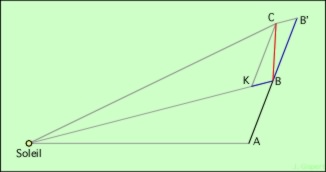
Quelle est l’aire du triangle SBC ?
 >
>
Nous avons vu que le triangle SBB’ a même aire que le triangle SAB : surface(SBB’) = surface(SAB). Montrons maintenant que le triangle SBC a même aire que le triangle SBB’. C’est très simple, car ils ont un côté commun SB. Prenons-le pour base. La hauteur de chacun des triangles est la projection du troisième sommet (respectivement C et B’) sur cette base, donc les projections de C et B’ respectivement. Mais CB’ est parallèle à KB par construction. Les points C et B’ sont donc à la même distance de SB, et ces distances sont les hauteurs des deux triangles. Donc, les deux triangles ont même base et même hauteur, et leurs surfaces sont donc égales.
Puisque surface(SBB’) = surface(SAB), et que maintenant surface(SBB’) = surface(SBC), on obtient par transitivité que surface(SBC) = surface(SAB). Nos deux triangles ont donc bien la même aire.
SA et SB étant les rayons-vecteurs de la planète, on a démontré que le rayon-vecteur balaye des aires égales en des temps égaux, c’est-à-dire la seconde loi de Kepler !
Mais aussi, les points S, A et B définissent un plan. Puisque K est sur SB, K est dans ce plan aussi. Par le principe d’inertie, B’ est sur la ligne AB, donc dans le même plan également. Par conséquent, tout le parallélogramme ABB’C est dans ce plan, donc en particulier C. Ce qui montre que la trajectoire de la planète est dans un plan, c’est la première loi de Kepler !
De plus, la démonstration ne dépend pas de la longueur du segment BK, qui représente l’intensité de la force. Par conséquent, cette loi est valable pour toute force dirigée vers un centre, ce que l’on appelle une force centrale.
Enfin, remarquez que si l’on considère des instants de plus en plus brefs, les déplacements considérés sont de plus en plus petits, et la ligne brisée s’approche de plus en plus de l’orbite réelle. Cette remarque permet d’entrevoir le calcul infinitésimal, nommé maintenant calcul différentiel, inventé indépendamment par Newton et Liebniz. Toutefois, ces idées d’approximations successives étaient déjà présentes dans la pensée grecque antique, pour la mesure des surfaces.
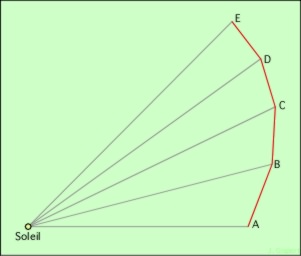 >
>
positions successives d’une planète
Un raisonnement géométrique de nature semblable a amené Newton à découvrir la loi de la Gravitation Universelle, c’est-à-dire la dépendance en 1/R2 de la force exercée par le Soleil.
Reprenant le dernier schéma, puisque les temps t entre A et B, et entre B et C sont égaux, on peut les considérer comme unitaires : t = 1. Alors, la vitesse de la planète entre A et B est égale à AB / t = AB / 1 = AB. De même pour tous les autres segments, puisque les temps sont égaux. Pour définir correctement la vitesse, il faut tenir compte de la direction de chacun des segments (ce sont les vecteurs vitesse).
Reprenons un schéma précédent, en y ajoutant le segment AK :
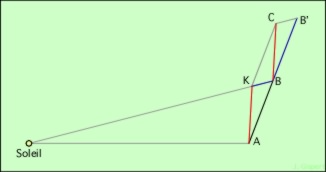
KBB’C est un parallélogramme, donc BB’ = KC. D’autre part, AB = BB’ par le principe d’inertie. Donc, AB = KC. De plus, ces segments sont parallèles. Donc, KCBA est aussi un parallélogramme. Par suite, AK = BC.
Or AB mesure la vitesse de la planète entre A et B, et BC mesure sa vitesse entre B et C. Donc, AK mesure la vitesse entre A et K ; l’égalité de AK avec BC montre que AK mesure aussi la vitesse entre B et C. La vitesse tient compte de la mesure et de la direction. Elle s’exprime par des vecteurs.
Si vous ajoutez les deux vecteurs ![]() et
et ![]() , vous obtenez le vecteur
, vous obtenez le vecteur ![]() .
.
Ou encore : ![]() .
.
Les deux vecteurs ![]() et
et ![]() représentant les vitesses en A et B, leur différence
représentant les vitesses en A et B, leur différence ![]() est la variation de vitesse. Donc,
est la variation de vitesse. Donc, ![]() est d’autant plus long que la variation de vitesse Δv de la planète entre les couples de points (A, B) et (B, C) est plus grande. La mesure de BK est proportionelle à Δv.
est d’autant plus long que la variation de vitesse Δv de la planète entre les couples de points (A, B) et (B, C) est plus grande. La mesure de BK est proportionelle à Δv.
Si on change l’intervalle de temps, la variation de vitesse changera également. Donc, BK représente la variation de vitesse par unité de temps, et :
BK ∝ Δv / Δt
Et puisque BK est proportionnel à la force :
F ∝ Δv / Δt
Newton a ainsi montré que la force est proportionnelle à la variation de vitesse par unité de temps, ce qu’on appelle l’accélération
Considérons maintenant le cas particulier d’une orbite circulaire. Les différents rayons-vecteurs SA, SB, SC… sont tous égaux au rayon R de l’orbite. Les intervalles de temps étant toujours égaux, le schéma devient :
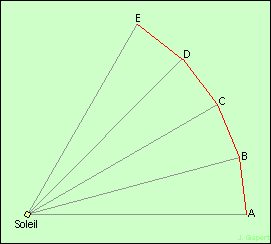
Lorsqu’on passe du point A au point B, on se retrouve à la même distance au Soleil (SB = SA). Même si la force qu’on recherche dépend de la distance au Soleil, elle ne change pas ici puisqu’on reste à la même distance. Le choix du cercle permet ainsi de s’affranchir de la dépendance de la force par rapport à la distance.
Passant de A à B, la figure a simplement tourné de 15° (ce nombre est un choix arbitraire pour le schéma ; il est bien évident que dans le calcul infinitésimal, il faut prendre un pas considérablement plus petit). On construit ainsi, pas par pas, un polygone régulier, qui approche le cercle.
Les segments AB, BC, CD… représentent chacun l’espace parcouru pendant l’unité de temps choisie. Donc la vitesse de la planète pendant cet intervalle. Ils sont tous égaux en longueur, donc la vitesse est constante en module. Par contre, elle est tout le temps variable en direction. Et lorsque la planète fait un tour complet, le vecteur vitesse fait aussi un tour complet. On peut représenter tous ces vecteurs vitesses en les plaçant à une même origine (le cercle dessiné par les extrémités des rayons-vecteurs est l’hodographe du mouvement) :

Les rayons rouges sont les segments AB, BC… du schéma précédent. Ils sont tous égaux au module v de la vitesse. Quelle est la variation de la vitesse au cours d’un intervalle de temps ? C’est le petit déplacement de l’extrémité du rayon, soit le chemin entre VA et VB sur le graphique (et qui correspond à BK sur le premier graphique). Pour une orbite complète, la variation totale de vitesse est donc 2 π v. Et par unité de temps, c’est donc Δv / Δt = 2 π v / T, puisque la vitesse est constante.
F ∝ Δv / Δt = 2 π v / T.
D’autre part, la vitesse moyenne de la planète sur son orbite est la distance parcourue divisée par le temps mis pour cela. Le temps est la période T de la planète (son année). Et la distance parcourue est la circonférence de l’orbite 2 π R. Donc, la vitesse moyenne est vm = 2 π R / T. Puisque l’orbite est circulaire, la vitesse instantanée est égale à la vitesse moyenne v = vm = 2 π R / T.
On remplace donc v par sa valeur :
F ∝ 2 π v / T = 2 π ( 2 π R / T) / T = 4 π2 R / T2
Il est temps d’utiliser la troisième loi de Kepler :
a3 / T2 = cste = R3 / T2 puisque le demi grand-axe a est le rayon R du cercle. Et donc : T2 = R3 / cste. Reportons cette valeur dans l’expression précédente :
F ∝ 4 π2 R / T2 = 4 π2 R / (R3 / cste) = 4 π2 cste / R2
En regroupant les constantes sous le même terme k :
Ainsi est trouvée la variation de la force gravitationnelle en 1 / R2. Elle résulte d’une longue chaîne de travail comprenant les excellentes observations de Mars par Tycho-Brahé, puis l’astucieuse exploitation de ces données par Kepler pour en déduire les lois du mouvement des planètes, et enfin l’abstraction de ces lois faite par Newton pour en déduire la force agissante.
La loi obtenue par Newton lui a permi de démontrer les lois de Kepler. C’est-à-dire de faire la démarche inverse : admettant sa loi, démontrer celles de Kepler. Puisque celles-ci sont validées par l’observation, elles valident en retour la loi de Newton.
La démarche utilisée par Newton est de même nature géométrique. Elle se trouve, ainsi que les démonstrations précédente, dans un petit livre très intéressant de D. et J. Goodstein intitulé "Le mouvement des planètes autour du Soleil".
Ensuite, les lois de Kepler sont apparues comme des approximations, qui correspondent à un cas idéal. La loi de Newton a permis de prendre en compte un cas bien plus proche de la réalité, dans lequel on tient compte de l’influence de Jupiter et Saturne par exemple dans l’étude du mouvement de Mars. Mais la loi de Newton a montré aussi la difficulté du problème du mouvement gravitationnel, lorsque plus de deux corps sont en interaction : il n’existe pas de solution analytique au problème. Seules des solutions numériques (méthode des perturbations spéciales), ou des approximations sous forme de séries de fonctions (méthode des perturbations générales), sont possibles.
---=OO=---