Historique de Marseille
| liens |
le 02/01/25
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 02/01/25 |
||||
| �� Réactions nucléaires | |||||||
Avant d’étudier les réactions nucléaires, il est bon de savoir ce que sont les atomes (spécialement les noyaux atomiques), et d’avoir quelques notions sur les particules élémentaires. Pour cela, la lecture du chapitre qui leur est consacré peut être utile.
La notion de réaction est bien mieux connue dans le domaine de la chimie que dans le domaine nucléaire. Aussi ferons-nous d’abord une claire différence entre les deux.
Une réaction chimique consiste à prendre deux molécules (associations d’atomes), à en extraire les constituants, et à les recoller différement. Par exemple, NaOH (une molécule de soude caustique, constituée d’un atome de sodium Na, un atome d’oxygène O, et un atome d’hydrogène H) et HCl (une molécule d’acide chlorhydrique, constituée d’un atome d’hydrogène H et d’un atome de chlore Cl) vont donner NaCl (une molécule de sel de cuisine, ou chlorure de sodium, constituée d’un atome de sodium Na et d’un atome de chlore Cl) et H2O (une molécule d’eau, constituée d’un atome d’oxygène O et de deux atomes d’hydrogène H). On écrit plus simplement :
NaOH + HCl → NaCl + H2O
On remarque que le nombre d’atomes de chaque espèce est le même avant et après la réaction (à gauche et à droite de la flèche). Ils sont conservés. On dit que la réaction est équilibrée.
Ce sont les électrons qui collent les atomes dans une molécule, par l’interaction électromagnétique. Les réactions chimiques réarrangent les atomes, de telle manière que leur stabilité électronique augmente.
Le nombre d’électrons de chaque atome détermine donc sa capacité plus ou moins grande à participer à ces réactions, c’est-à-dire ses propriétés chimiques. Il assure aussi la neutralité électrique de l’atome, donc il est identique au nombre de protons du noyau. En fin de compte, c’est donc le nombre de protons d’un noyau qui détermine, indirectement, ses propriétés chimiques.
Pour définir un noyau, on donne le nombre de protons qu’il contient, on le note Z, et on le nomme numéro atomique. Deux éléments chimiques différents (Na et Cl par exemple) ont des numéros atomiques différents (11 et 17 respectivement) ; deux isotopes d’un même élément possèdent le même numéro atomique (comme l’hélium 3 et l’hélium 4 ; ce sont deux noyaux d’hélium parce que leur Z est le même : 2). Pour préciser l’isotope considéré, il faut donner le nombre de neutrons. Mais l’habitude est autre, on donne la masse atomique, c’est-à-dire le nombre de nucléons (protons + neutrons), notée A. Par exemple, pour le carbone 14, on a Z = 6, A = 14. Le nombre de neutrons est N = A - Z = 8. Pour caractériser totalement un isotope d’un élément, on note A et Z à gauche du symbole, en haut pour A et en bas pour Z. (on peut remarquer que ceci est une redondance : He représente un atome d’hélium, donc qui possède 2 protons ; il est donc redondant, mais bien pratique, de noter le nombre Z)
Le carbone 14 est le plus célèbre des isotopes du carbone, et sert à dater les résidus organiques anciens. En fait, un morceau de carbone ordinaire est constitué d’un mélange d’atomes, ayant tous 6 protons (carbone), et dont la plupart possèdent 6 neutrons, mais quelques uns en ont 7 ou 8 . On les nomme carbone 12 12
6C, carbone 13 13
6C, et carbone 14 14
6C.
Un autre exemple célèbre est l’eau lourde, dont les molécules sont constituées avec des atomes d’hydrogène lourd ou deutérium : un proton et un neutron 2
1H. La masse d’un tel atome est à peu près double de celle de l’hydrogène normal. Il existe aussi un hydrogène super lourd, avec deux neutrons, nommé tritium 3
1H.
Avez-vous déjà bu de l’eau lourde ? Sans aucun doute ! En effet, l’eau des océans en contient un faible pourcentage. Il y en a donc un peu dans nos bouteilles d’eau minérale, et dans l’eau du robinet.
Retenez bien que les réactions chimiques portent sur les nuages électroniques, sans jamais toucher aux noyaux ! La chimie est produite par l’interaction électromagnétique. C’est pour cette raison qu’un atome de plomb restera toujours, quelque réaction chimique que vous puissiez lui faire subir, un vulgaire atome de plomb… Le rêve de l’alchimiste ne risquait pas de se réaliser de cette façon !
Mais la physique nucléaire donne la solution, et nous allons voir qu’on est capable de transformer un noyau de plomb en noyau d’or, à condition de payer le prix en énergie, ce qui ruinera (c’est le cas de le dire) tout espoir dans ce domaine. On sait le faire, mais ça coûte cher ! C’est peut-être bien mieux ainsi… La Pierre Philosophale est un accélérateur de particules !
Les réactions que nous allons étudier maintenant portent sur les noyaux (latin nucleus), c’est pourquoi on les nomme réactions nucléaires. C’est l’interaction forte qui en est responsable.
De la même manière qu’une réaction chimique, une réaction nucléaire consiste à prendre certains composants, et à les réordonner. Elle s’écrit donc de manière semblable, avec un groupe d’éléments à gauche, une flèche au centre, et un autre groupe à droite. Comme pour les réactions chimiques, il faut respecter un équilibre entre les deux membres : ils doivent présenter les mêmes caractéristiques.
Les constituants sont des noyaux atomiques (constitués de protons et neutrons), et la réaction les réarrange en deux nouveaux noyaux, en conservant le nombre de nucléons. Par exemple, un atome de 13
6C (carbone 13, 6 protons et 7 neutrons) et un atome d’hydrogène 1
1H (1 proton) vont donner un atome de 14
7N (azote 14, 7 protons et 7 neutrons). Ce qui s’écrit :
13
6C + 1
1H → 14
7N + γ
Dans cette réaction, le γ (gamma) représente un photon qui est émis, et qui emporte de l’énergie. Nous verrons un peu plus loin pourquoi. Vérifiez que le total des exposants à gauche (13 + 1) et à droite (14) est le même ; idem pour les indices (6 + 1 = 7). Ceci signifie que les nucléons se sont conservés, et réarrangés.
Remarquez que dans la réaction nucléaire, l’équilibre chimique est rompu : il y a un atome de carbone à gauche, et il n’y en a pas à droite. Par contre, le bilan de neutrons et protons est respecté : (6p + 7n) + 1p = 7p + 7n. Il s’agit d’une réaction nucléaire à proprement parler. Il est normal que l’équilibre chimique ne soit pas respecté, puisqu’il concerne l’interaction électromagnétique, alors que les réactions nucléaires dont on s’occupe concernent l’interaction forte.
Il existe d’autres réactions, dans lesquelles le nombre de nucléons est conservé, mais pas leur genre. Un proton peut se changer en neutron, et réciproquement. La responsable de ces changements est l’interaction faible, et des électrons sont concernés par ces transformations. Une réaction béta change un proton en neutron, ou l’inverse, ce qui fait que le noyau qui la subit n’est plus de la même espèce chimique. C’est ce qui permet certaines transmutations.
Les réactions nucléaires sont de plusieurs types, selon les transformations produites. On distingue tout d’abord les réactions de fusion, et les réactions de fission. Dans les premières, on ajoute des composants pour former des noyaux plus lourds, dans les secondes au contraire, on casse un gros noyau pour en produire de plus petits. Voici deux exemples de telles réactions (voir le tableau de Mendéléev pour suivre les réactions) :
| fusion | 2 1H + 1 1H → 3 2He + γ |
| fission | 226 88Ra → 222 86Rn + 4 2He |
L’hydrogène fusionne pour donner de l’hélium (4 noyaux d’hydrogène donnent un noyau d’hélium, grâce à la désintégration béta), mais l’hélium lui-même peut fusionner pour donner des éléments plus lourds encore, carbone (3 noyaux d’hélium donnent un noyau de carbone), oxygène, azote. Dans ce genre de réactions, il faut comme précédemment faire le bilan énergétique. Toutes les réactions de fusion produisent de l’énergie. Mais on s’aperçoit que l’énergie qu’elles dégagent est de plus en plus faible à mesure qu’on considère la fusion d’éléments plus lourds (en partant du plus léger, l’hydrogène). Lorsqu’on arrive à synthétiser du fer, la différence s’annule. Le bilan énergétique devient défavorable : à partir du fer, la réaction consomme de l’énergie au lieu d’en produire. On peut dire cela autrement : pour A < 56, la réaction est exothermique (productrice d’énergie), au-dessus, elle devient endothermique (consommatrice d’énergie).
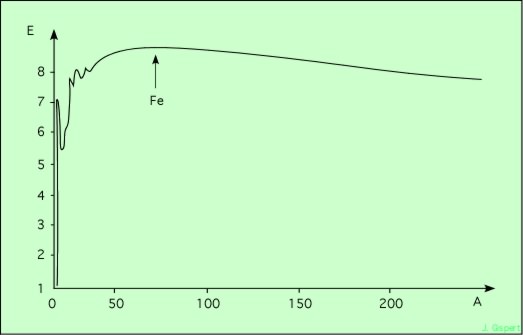
Energie de liaison par nucléon
Ce schéma montre l’énergie de liaison par nucléon, entre les nucléons qui constituent un noyau atomique. Pour que ceci ait un sens, on a divisé l’énergie totale de liaison à l’intérieur de l’atome par le nombre de nucléons. On montre ainsi une énergie moyenne par nucléon.
(26 mp + 30 mn - mFe) / 56
où mp = masse du proton, mn = masse du neutron, mFe = masse du noyau de fer 56. Il faut exprimer les masses en eV/c2 (eV signifie électron-volt, c’est une petite unité d’énergie), équivalence justifiée par l’équation d’Einstein E = m c2.Ce qui est remarquable, c’est que la courbe montre un maximum au niveau du fer. Ceci signifie que les nucléons dans un noyau de fer sont plus fortement liés à leurs voisins que dans tout autre noyau ! Les noyaux de fer sont donc les plus stables : pour les casser, il faut plus d’énergie que pour tout autre.
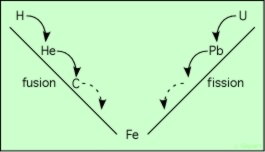
Ce schéma représente une sorte d’entonnoir, ayant le fer au centre. Ce dernier est le point de stabilité maximum. La fusion des divers éléments, depuis l’hydrogène jusqu’au fer, suit la pente descendante de gauche. De même, la fission de l’uranium suit l’autre pente. Ceci symbolise le caractère exothermique de la fusion, jusqu’au fer. Par contre, si on voulait fusionner des éléments plus lourds que le fer, il faudrait remonter la pente (du côté droit), donc fournir de l’énergie. Il faudrait fournir de l’énergie aussi de l’autre côté pour briser des atomes plus légers que le fer. Dans une étoile, il ne serait pas possible de fournir de l’énergie pour fusionner au-delà du fer, car ceci diminuerait l’énergie disponible, donc la pression, et romprait l’équilibre de l’étoile. Cette propriété des atomes détermine donc le fonctionnement et le devenir des étoiles.
Ceci ouvre une voie de recherche : quelle est la stabilité de chaque noyau ? Lorsqu’on teste une nouvelle colle, on se demande si elle va tenir… Cette question se pose pour des éléments chimiques différents, mais aussi pour les isotopes d’un même élément, puisque ce sont des noyaux ayant un nombre différent de neutrons. Certains noyaux ne risquent-ils pas de se casser ?
Une réaction nucléaire doit se faire (dans le sens de la flèche qui la représente) du moins stable vers le plus stable, comme un pendule évolue vers sa position d’équilibre. Des noyaux légers auront donc tendance à s’assembler (par réaction de fusion), alors que des noyaux lourds auront tendance à se briser (par réaction de fission). Dans les deux cas, ils se rapprochent du fer.
Bien que les réactions de fusion et de fission soient de nature très différente, elles procèdent des mêmes principes fondamentaux de la physique.
La radioactivité a été découverte par Becquerel en 1896 sur des sels d’uranium, puis confirmée peu après par Marie Curie sur le thorium. Les radionuclides (éléments radioactifs) les plus répandus sont l’uranium 238 (238
92U), le thorium 232 (232
90Th) et le potassium 40 (40
19K). Un champ magnétique partage les rayonnements produits par des sels uraniques (sels de l’uranium ; ce sont des molécules chimiques contenant au moins un atome d’uranium) en trois faisceaux différents, nommés historiquement alpha, béta et gamma. Ce sont les trois formes de radioactivité. Les trois consistent en l’émission d’une particule, avec les changements associés.
La radioactivité alpha est l’émission d’une particule alpha (noyau d’hélium 4) par un noyau atomique. On dit que le noyau est excité (son énergie est trop grande, ses nucléons s’agitent de façon désordonnée)) ; il se désexcite par cette émission, en se brisant. C’est une réaction nucléaire spontanée. La réaction donnée en exemple de fission plus haut est une radioactivité alpha. On reconait ces réactions au noyau d’hélium 4 présent à droite de la flèche.
La particule alpha doit avoir une grande stabilité pour se comporter dans cette réaction comme un tout. Ceci s’explique en particulier parce qu’elle est composée de 2 protons et 2 neutrons. Les deux protons (deux fermions identiques) se mettent en position de spin antiparallèle, les deux neutrons aussi (ce sont aussi deux fermions identiques). Ainsi, le principe d’exclusion de Pauli est respecté. Si on ajoute une cinquième particule, proton ou neutron, son niveau d’énergie devra être plus grand pour respecter le principe d’exclusion. La particule alpha est donc, de ce point de vue, la plus grosse possible au niveau d’énergie minimum, ce qui explique au moins en partie sa stabilité.
Dans la radioactivité béta, un électron est éjecté à la place d’une particule alpha. Une réaction s’écrit :
n → p + e- + νe
où n représente un neutron, p un proton (qu’on aurait pu noter aussi 1
1H), et e- un électron négatif (un véritable électron, celui portant une charge positive étant nommé positron), νe est un antineutrino électronique. Elle ne porte pas sur un noyau, mais sur un nucléon, qui peut faire partie d’un noyau. Si c’est le cas, le noyau est modifié (il aura un proton de plus, et un neutron de moins).
Cette réaction est nommée désintégration β-. Plus profondément, un quark d du neutron est changé en un quark u. Le neutron (udd) est donc devenu proton (uud). Le changement de saveur du quark s’accompagne de l’émission d’un boson W-, qui se désintègre immédiatement en un électron et un antineutrino, complétant la réaction.
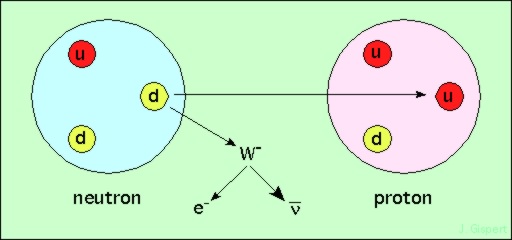
La réaction notée plus haut est en fait un résumé, qui en regroupe deux (le boson W fugace n’étant pas noté).
Il existe une radioactivité béta complémentaire, qui met en jeu le positron, antiparticule de l’électron :
p → n + e+ + νe
Elle est nommée désintégration β+. On voit que le proton à gauche porte une charge positive, qui est emportée à droite par le positron. La réaction est donc électriquement équilibrée.
Ces deux réactions ne sont pas symétriques l’une de l’autre quand à leur fréquence. Le proton étant un peu plus léger que le neutron, la réaction β- peut se produire spontanément, alors que la réaction β+ nécessite un apport d’énergie. Celle-ci est apportée sous forme d’énergie cinétique dans la fusion de deux protons qui donne un noyau de deutérium (première réaction de la chaîne proton-proton).
Enfin, on note des réactions symétriques des éjections : ce sont des absorptions. L’électron (ou positron) n’est pas produit (donc à droite de la flèche), mais consommé (donc à gauche). Elles sont possibles toujours par l’interaction faible, et justifiées par les mêmes principes :
p + e- → n + νe
n + e+ → p + νe
où νe représente un antineutrino électronique.
Ces réactions sont très simples à écrire : il suffit d’équilibrer les éléments à gauche et à droite. Ici, la charge doit être conservée, et vous pouvez vérifier, dans la dernière réaction par exemple, que l’on a à gauche neutre (le neutron), et + (le positron), donc 1 charge positive ; à droite + (le proton) et neutre (le neutrino). Donc un bilan d’une charge positive de chaque côté, la réaction est bien équilibrée.
De plus, l’énergie doit aussi se conserver, ce qui justifie la présence du neutrino (électriquement inutile). C’est d’ailleurs par ces réactions que le neutrino a été imaginé par Enrico Fermi pour équilibrer l’énergie de la réaction, puis observé expérimentalement plus tard.
Pour que la réaction soit totalement équilibrée, il faut aussi assurer la conservation du nombre leptonique. Les leptons sont les particules légères : électron et positron, neutrinos. Le nombre de ces particules doit être le même à gauche (avant) et à droite (après).
Le nombre leptonique est noté +1 pour les particules, -1 pour les antiparticules. L’électron est une particule, son nombre leptonique est +1. Le positron est son antiparticule, son nombre leptonique est -1. Remarquez que le nombre leptonique est l’opposé de la charge électrique, ceci pour des raisons historiques. Le nombre leptonique de toutes les autres particules, qui ne sont pas de leptons, est bien sûr 0.
De la même manière, le nombre leptonique d’un neutrino est +1 pour la particule, et -1 pour l’antiparticule. Ceci permet de comptabiliser les particules et les antiparticules pour équilbrer la réaction.
Examinons de ce point de vue la réaction :
n → p + e- + νe
A gauche de la flèche, il y a un neutron (nucléon), et aucun lepton (ni électron, ni neutrino). Par conséquent, le nombre leptonique à gauche vaut 0.
A droite de la flèche, le neutron étant devenu proton avec une charge électrique +1, on a ajouté un électron de charge électrique -1 pour assurer l’équilibre électrique. Mais de ce fait on a jouté un lepton, de charge leptonique +1. On doit donc ajouter encore une antiparticule leptonique neutre (neutre pour ne pas détruire l’équilibre électrique, antiparticule leptonique pour apporter un nombre leptonique -1). C’est l’anti neutrino électronique.
La radioactivité gamma, enfin, est simplement une perte d’énergie sous forme de rayonnement électromagnétique. La particule éjectée est le photon associé à l’onde. C’est par elle qu’un noyau se désexcite. Le niveau d’énergie d’un photon gamma est bien supérieur aux niveaux de fluorescence, qui concernent les électrons périphériques d’un atome.
| type | particule éjectée | interaction responsable |
|---|---|---|
| alpha | particule alpha (noyau 4 2He) | forte |
| béta | électron ou positron | faible |
| gamma | photon | électromagnétique |
Les réactions de fusion sont celles qui combinent deux noyaux, pour donner un noyau plus lourd.
Nous avons vu plus haut que le noyau d’hélium était plus léger que les 4 noyaux d’hydrogène qui l’ont produit. L’énergie par nucléon a augmenté, au détriment de la masse. La masse par nucléon a diminué.
Nous allons considérer la fusion de l’hydrogène, telle qu’elle se produit dans les étoiles. Ce n’est pas une réaction simple, mais un enchaînement de plusieurs réactions successives. Plusieurs enchaînements différents peuvent se produire.
Deux noyaux d’hydrogène (protons) portant chacun une charge électrique positive, se repoussent très fortement (répulsion coulombienne). Cette répulsion est si forte, à courte distance, que le noyau s’entoure d’une barrière, dite barrière coulombienne. Pour qu’un proton arrive au contact d’un noyau, il doit franchir la barrière coulombienne.
Mais les noyaux sont aussi sensibles à une autre force, qui agit de très près comme une colle. Si on rapproche deux protons assez près l’un de l’autre, malgré la répulsion électrique, on arrive à les coller, et ils le resteront (s’il n’y avait pas d’autre problème, comme nous le verrons plus loin). Mais il faut pour cela qu’ils soient vraiment très, très proches… L’interaction forte qui les attache est beaucoup plus intense que la répulsion électromagnétique, mais elle ne s’exerce pratiquement qu’au contact.
Mettez de la colle néoprène sur deux aimants de même polarité qui se repoussent ; rapprochez-les l’un de l’autre en forçant ; si vous arrivez à les faire toucher, la colle va les retenir l’un contre l’autre. La répulsion magnétique des aimants joue ici comme la répulsion électromagnétique des protons ; la colle agit comme l’interaction forte qui colle les protons dans le noyau d’un atome. La colle n’agit pas à distance !
Si vous agitez le groupe ainsi constitué, vous arriverez facilement à séparer les deux aimants, leur groupe explosant littéralement sous la répulsion électromagnétique. Le noyau simulé est instable, et se désintègre à la moindre excitation.
La répulsion électromagnétique des protons agit comme une barrière qui les empêcherait de se rapprocher. On la nomme barrière de potentiel. Considérons un proton au repos, et un autre qui s’en approche. Pour qu’il franchisse la barrière de potentiel dressée autour du premier, il faut qu’il ait une grande vitesse, et donc qu’il soit à très haute température. Ceci n’est pas réalisé dans les conditions qui règnent sur Terre, c’est pourquoi il est si difficile de construire un réacteur de fusion comme ITER.
Et malgré les 15 millions de degrés qui règnent au centre du Soleil, la vitesse des protons est encore trop faible pour les rapprocher suffisamment. Si la mécanique classique s’appliquait, la fusion de l’hydrogène n’y serait pas possible. Mais un phénomène de mécanique quantique, qui ne se produit pas dans le monde à notre échelle (macroscopique), permet à un proton de franchir la barrière parfois, sans disposer de la vitesse qui serait nécessaire (en mécanique classique). Tout se passe comme s’il avait traversé la barrière. Pour cette raison, ce phénomène est nommé effet tunnel.
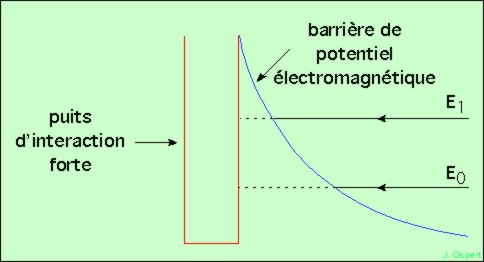
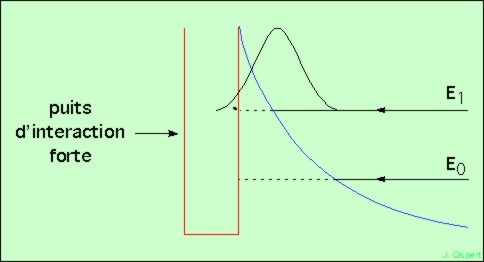
Ce schéma montre, en rouge, le puits de potentiel attractif de l’interaction forte. Pour que les deux protons soient collés, il faut que le second tombe dans le puits de potentiel du premier. Si le second arrive de la droite, avec l’énergie E0 (correspondant à sa vitesse, donc à sa température), il ne pourra pas franchir la barrière électromagnétique, qui est trop haute. A l’énergie E1, c’est encore impossible. Cependant, il arrive qu’un proton puisse passer, même si son énergie est trop faible. Il traverse alors la barrière de potentiel.
Ceci demande une petite explication. Nous avons dit que toute particule possédait une onde associée. Cette onde indique l’endroit de l’espace où se trouve la particule.
|
La particule est figurée par un petit cercle, et son onde associée au-dessus. On remarque que la particule se trouve au centre de l’onde. En fait, cette situation est la plus probable. Mais la particule peut se trouver n’importe où au-dessous de l’onde. La probabilité qu’elle se trouve en un point donné est proportionnelle à la hauteur (l’amplitude) de l’onde en cet endroit. La particule a donc peu de chances de se trouver sur une aile de l’onde, mais c’est possible. |
En reprenant le schéma de l’effet tunnel, on comprend que, lorsque le centre de l’onde heurte la barrière de potentiel, le proton se trouve en général bloqué. Mais parfois, s’il se trouve sur l’aile avant de l’onde, il se trouve de l’autre côté de la barrière, qui est par conséquent franchie :
Lorsque deux protons réussissent à se coller, ils forment un noyau ayant deux charges positives. Il n’aura donc pas les mêmes propriétés chimiques que l’hydrogène. Il s’agit d’un élément différent : c’est un noyau d’hélium. Comme il n’est constitué que de ces seuls protons, on dit qu’il s’agit d’hélium 2, et on le note 2
2He. Le 2 en haut à gauche indique le nombre total de particules qui constituent le noyau, et celui placé en bas (s’il est présent, mais le symbole chimique le rend superflu : He = Hélium ⇒ 2 protons) représente le nombre de protons. Cet hélium est donc constitué de deux nucléons, dont deux protons.
La répulsion électromagnétique, bien que moins intense que l’interaction forte, agit suffisament sur les deux protons pour faire éclater le noyau au bout d’un temps très bref (quelques milliardièmes de seconde…). Aussi le noyau d’hélium 2 tout juste formé se brise, et on retrouve les deux protons de départ (deux noyaux d’hydrogène). Comme si rien ne s’était passé !
Remarquez que les deux protons, étant deux fermions identiques, doivent obéir au principe d’exclusion. Ils doivent donc se placer des des états de spin différents (+1/2 pour le premier, -1/2 pour le second). L’ennui est que cet état antiparallèle possède une énergie négative, et les protons ne sont plus liés !
La fusion de deux noyaux d’hydrogène (protons) ci-dessus se note :
1
1H + 1
1H ↔ 2
2He
La double flèche indique que la réaction est réversible. Les deux protons sont notés 1
1H (puisque ce sont des atomes d’hydrogène 1), et le noyau produit est un 2
2He (hélium, constitué de deux protons ; ce noyau est surtout appelé diproton, étant donnée son instabilité : ce sont deux fermions identiques, qui devraient avoir des spins anti-parallèles, mais ceci leur donnerait une énergie de laison négative !).
La désintégration qui se produit très rapidement redonne donc les deux protons :
2
2He → 1
1H + 1
1H
Ces deux réactions se produisent en permanence dans le Soleil, et le très faible intervalle de temps, non nul, entre les deux permet d’entretenir en permanence une très faible proportion d’hélium 2.
Mais un autre phénomène se produit parfois : l’un des deux protons se débarrasse de sa charge électrique, en émettant un électron positif (positron) avant que le diproton n’éclate ; il devient alors un neutron par radioactivité β+ (plus parce que la particule éjectée est un positron). Un positron est exactement semblable à un électron, mais porte une charge positive et non négative. C’est l’antiparticule de l’électron, ou anti-électron.
La réaction qui se produit dans le noyau d’hélium 2 s’écrit :
2
2He → 2
1H + e+ + νe
où νe est un neutrino électronique.
Cette coïncidence est heureusement très rare, car sinon le Soleil aurait explosé à sa naissance !
Ainsi, l’assemblage 2
1H obtenu comporte maintenant un proton et un neutron. Entre eux, pas de répulsion électromagnétique ni de problème de spin, et donc l’assemblage est stable. Ce noyau va pouvoir vivre longtemps. On reconnait un noyau de deutérium, ou hydrogène lourd, noté D ( D = 2
1H). L’ensemble dégage 1,44 MeV d’énergie, emportée par le positron et le neutrino.
Les réactions ne s’arrêtent pas là. Le noyau de deutérium obtenu va capturer un nouveau proton, qui restera chargé (qui restera proton). Le nouvel assemblage comporte donc deux protons et un neutron ; c’est donc un noyau d’hélium, mais qui comporte un neutron de plus que celui qu’on a vu plus haut. De même qu’il existe plusieurs isotopes d’hydrogène, il existe plusieurs isotopes d’hélium : celui-ci est l’hélium 3 (car il comporte 3 nucléons), noté 3
2He.
La réaction s’écrit :
2
1H + 1
1H → 3
2He + γ
La réaction produit, en plus du noyau d’hélium 3, un photon gamma de haute énergie. Elle dégage 5,49 MeV, emportés par le photon. Ce photon constituera une partie de l’énergie produite dans le Soleil. Le noyau obtenu est stable, grâce au neutron qui colle les deux protons par interaction forte, sans les repousser par interaction électromagnétique. Il joue le rôle de liant. Les deux protons doivent avoir leurs spins opposés ; pour le neutron, il est indifférent.
Si vous collez un morceau de métal (non magnétique) sur les deux aimants, avec la même colle, vous renforcez la liaison. Vous obtenez alors un noyau stable ayant le même nombre d’aimants (de protons). Le morceau de métal joue le rôle d’un neutron, qui est sensible à l’interaction forte, mais n’exerce pas de répulsion électrique. L’assemblage est un isotope, ayant le même nombre de protons (aimants) et un nombre différent de neutrons (morceau de métal).
Et les réactions continuent, mais de façon un peu différente. Deux noyaux d’hélium 3 nouvellement formés se rencontrent, et fusionnent en se débarrassant de deux protons :
3
2He + 3
2He → 4
2He + 1
1H + 1
1H + γ
Cette réaction produit 12,86 MeV. Le résultat est un noyau comportant maintenant deux protons et deux neutrons ; c’est de l’hélium 4 (car il comporte 4 nucléons) 4
2He. On l’appelle aussi particule alpha (Lorsqu’on a découvert la radioactivité, on a identifié trois sortes d’émissions, nommées respectivement alpha, béta et gamma. La première consiste en éjection de noyaux d’hélium 4, la seconde d’électrons, et la dernière de rayonnement électromagnétique gamma). Ce noyau est très stable, et ne subira plus d’autre réactions, sauf si la température s’élève très fortement (100 millions de degrés).
La raison qui empêche une nouvelle fusion est simple : le noyau possède maintenant deux charges électriques, qui vont repousser vivement tout autre noyau candidat à la fusion. Mais si la barrière de potentiel était franchie, la fusion n’aurait pas lieu pour autant. Nous avons vu (radioactivité) que dans la particule alpha, les deux protons ont leurs spins antiparallèles, les deux neutrons aussi. Protons et neutrons étant des fermions différents, les quatre peuvent se trouver au minimum d’énergie. Si on veut ajouter un cinquième nucléon (ce serait 5
3Li), il devra se trouver obligatoirement sur un niveau d’énergie plus élevé, niveau qui est incompatible avec la stabilité du noyau !
On peut résumer tout ceci dans une animation, qui montre comment l’hydrogène fusionne en hélium.

| Fusion | Légende |
Cliquez sur l’animation pour la mettre en pause, ou la relancer.
L’animation montre le processus le plus simple de fusion de l’hydrogène qui se produit dans les étoiles, le processus dit PPI (proton-proton I), car sa première réaction consiste en la fusion de deux protons ; il en existe deux variantes, PPII et PPIII.
L’animation montre donc deux protons qui s’approchent l’un de l’autre. Lorsqu’ils arrivent en contact, grâce à leur vitesse (qu’on doit imaginer très grande), ils forment un diproton instable (ou noyau 2
2He), qui se brise presque intantanément.
La désintégration β+ d’un des protons au moment du choc est si rare, qu’il est impossible d’intégrer sa probabilité à l’animation. C’est pourquoi le bouton 'Forcer' permet de provoquer cette réaction, avant que le noyau d’hélium 2 ne se brise, pour former un noyau de deutérium. À partir de là, les autres réactions s’enchaînent : le noyau de deutérium rencontrant un nouveau proton (noyau d’hydrogène), forme avec lui un noyau ayant 2 protons et 1 neutron : c’est un noyau d’hélium 3 : 3
2He, stable.
Enfin, deux noyaux d’hélium 3 ainsi formés se rencontrent, et donnent un noyau d’hélium 4 : 4
2He, en rejetant 2 protons.
À chaque étape, l’animation montre en haut les réactions en cours, avec le temps moyen qu’elles nécessitent pour se produire. La désintégration béta d’un proton ne se réalise en moyenne qu’au bout de 14 milliards d’années, soit à peu près l’âge de l’univers... C’est le nombre colossal de protons dans l’étoile qui assure qu’un nombre important de telles réactions se produit à chaque seconde, fournissant l’énergie nécessaire à son équilibre.
Le second bouton permet de montrer ou cacher la légende de l’animation.
Les réactions sont mentionnée lorsqu’elles se produisent, avec le temps moyen nécessaire pour qu’elles se réalisent. Pour la première réaction, il s’agit de la durée de vie du noyau formé : l’hélium 2 ne subsiste que 10-20 seconde. Pour que le noyau ne se brise pas, il faut qu’une réaction béta transforme l’un des deux protons en neutron, pendant ce si bref intervalle de temps. Aussi, pour un proton donné, la transformation ne se fera en moyenne qu’au bout de 14 milliards d’années, plus que la durée de vie du Soleil. C’est le nombre extraordinaire de protons qui composent le cœur du Soleil qui permet de réaliser suffisamment de réactions pour assurer l’énergie de notre étoile.
Au total, 4 atomes d’hydrogène ont fusionné pour former un atome d’hélium 4. L’ensemble de ces réactions se résume à l’écriture simplifiée suivante :
4 1
1H → 4
2He + 2 e+ + 2 γ + 2 νe
On nomme cet ensemble de réactions chaîne proton-proton, d’après la première des réactions qui combine deux protons. En voici le résumé :
1
1H + 1
1H → 2
2He
Ce n’est pas la seule possibilité pour former un atome d’hélium à partir de l’hydrogène, nous le verrons plus loin.
On peut maintenant s’amuser à peser les atomes : on va avoir une bonne surprise ! L’atome d’hélium pèse moins que les 4 protons qui l’ont constitué. Comment se fait-il qu’un mur de briques soit plus léger que le tas de briques dont il est issu ?
La réponse est donnée par Einstein, et sa célèbre équation E = mc2 de la Relativité. La différence de masse entre les 4 protons et le noyau d’hélium a été transformée en énergie. La valeur de c étant très élevée (300.000.000 m/s), c2 est un coefficient multiplicateur prodigieux (presque 1017) : même si m est petite, l’énergie sera très grande. C’est la source de l’énorme énergie dispensée par le Soleil, est c’est parce qu’elle est très importante pour une faible perte de masse que le Soleil peut briller si longtemps…
Nous verrons plus loin d’autres réactions du même genre, qui se produisent dans le cœur des étoiles ou dans d’autres milieux encore plus extraordinaires.
Nous allons considérer la fusion de l’hydrogène que nous venons d’écrire (en ignorant les particules secondaires), sous la forme :
4 1
1H → 4
2He
Soit mp la masse d’un proton, et mh celle du noyau d’hélium 4. Appliquons l’équation d’Einstein E = m c2 :
| aux 4 protons | au noyau d’hélium |
| E4H = 4 mp c2 = 4 × (938,27 MeV / c2) × c2 = 3.753,08 MeV = 3,75308 GeV |
EHe = mHe c2 = (3,72738 Gev / c2) × c2 = 3,72738 Gev |
La réaction a diminué l’énergie totale du système (EHe est inférieure à E4H).
On retrouve un grand principe de la physique : les systèmes évoluent toujours vers un état de moindre énergie.
Exemple : si vous vous tombez une boule de pétanque sur le pied, ça vous fera d’autant plus mal qu’elle tombe de plus haut. Donc, plus elle est haute, plus elle possède d’énergie (c’est de l’énergie gravitationnelle). En tombant, elle trouve un état d’énergie moindre.
Attachez la boule à une ficelle. Faites balancer la boule, comme un pendule. Elle va osciller pendant un moment, puis se stabiliser dans la position la plus basse. Vous comprenez que le système a évolué vers son état d’énergie minimale. La boule ne peut pas descendre plus bas à cause de la ficelle.
Revenons maintenant à notre système à 4 nucléons. Nous avons deux états, l’un lié (He), l’autre libre (4 H). Le plus stable de ces deux états doit être celui de moindre énergie. C’est l’hélium, comme nous venons de le calculer. Et puisque l’énergie est équivalente à la masse, c’est aussi l’état de moindre masse. On comprend maintenant pourquoi le noyau d’hélium est plus léger que ses constituants séparés.
S’il était plus lourd que la somme de ses constituants, il évoluerait spontanément vers l’état libre, qui serait de moindre énergie.
Maintenant, un autre grand principe physique est la conservation de l’énergie. Elle ne doit ni augmenter, ni diminuer, dans un système isolé. Si les 4 atomes d’hydrogène antérieurs à la réaction présentent une énergie de masse supérieure à celle du noyau d’hélium produit, la différence d’énergie doit se retrouver ailleurs. Donc, le bilan doit être équilibré à gauche et à droite de l’équation. Il faut donc rajouter de l’énergie à droite, juste ce qui est nécessaire pour l’équilibre. Cette énergie est emportée par les positrons, neutrinos (sous forme d’énergie cinétique) et rayons gamma (énergie électromagnétique) émis.
La différence de masse correspond à l’énergie libérée :
Elibérée = EH - EHe = 3,753,08 MeV - 3,727,38 Mev = 25,7 MeV
Par rapport à la masse des 4 protons, cela représente : 25,7 / 3,753,08 = 0,00684 ou 0,7 %
Par conséquent, la fusion d’un gramme d’hydrogène produira l’équivalent de 0,007 g sous forme d’énergie. Nous allons faire le calcul dans le Système International. Il faut pour cela écrire la masse en kilogrammes.
0,007 g = 0,007 10-3 kg = 7 10-6 kg ;
c = 300.000 km/s, donc c = 300.000.000 m/s = 3 108 m/s.
Donc :
E = Δm c2 = 7 10-6 × (3 × 108)2 = 7 × 10-6 × 9 × 1016 = 63 1010 J/s
Ceci est équivalent à 25,7 MeV (exprimé dans une autre unité), qui sont dégagés pour chaque noyau d’hélium produit.
De quoi faire bouillir 10 000 tonnes d’eau ! Pour prendre 1 000 000 douches chaudes... soit une par jour pendant 2 700 ans.
Les 4 réactions qui composent cette chaîne n’ont pas toutes la même probabilité de se produire :
| réaction | type | attente | température |
|---|---|---|---|
| 1 1H + 1 1H → 2 2He + γ | nucléaire | 14 milliards d’années ! | 15 millions de degrés |
| 2 2He → 2 1H + e+ + ν | béta | moins de 10-8 s | |
| 2 1H + 1 1H → 3 2He + γ | nucléaire | 6 secondes | |
| 3 2He + 3 2He → 4 2He + 2 1 1H + γ | nucléaire | 1 million d’années |
Ces réactions se produisent à partir de 4 millions de degrés, mais le taux de réaction dépend de la température : plus c’est chaud, plus c’est efficace. Dans le cœur du soleil, la température est de 15 millions de degrés, et les réactions de cette chaîne sont très efficaces.
Toutes ces réactions ne se produisent pas à la même vitesse ; remarquons tout d’abord que la première n’est possible que par effet tunnel, dans une aile de l’onde associée au proton. La probabilité pour que le proton se trouve dans cette aile est très faible, et par suite la réaction ne se produit presque jamais. Pour un proton donné, dans le centre du Soleil (15 millions de degrés), l’attente est de 14 milliards d’années, en moyenne, avant que la réaction ne se produise. C’est dire que très peu d’hélium 2 est produit à chaque instant.
L’hélium 2 produit (2
2He) se désintègre en moins de 10-8 seconde en deux noyaux d’hydrogène (les deux protons de départ). C’est tout juste si le noyau d’hélium 2 a existé, sous une forme excitée. Cette réaction, très rare, permet cependant d’avoir à chaque instant un petit nombre de noyaux 2
2He présents dans le Soleil.
Dans les 10-8 secondes de vie de ce noyau, il est possible qu’une réaction béta désintègre l’un des protons en un neutron, pour donner le noyau de Deutérium qui permettra la réaction suivante (2
1H est noté D). Là encore, la probabilité est très faible (caractéristique des désintégrations béta), et presque tous les noyaux d’hélium 2 se brisent en noyaux d’hydrogène. C’est cette désintégration béta, par sa rareté, qui va ralentir énormément le processus de transformation de l’hydrogène en hélium. Heureusement, car sans cela, il y a longtemps que le Soleil aurait fini de briller !
Les deux réactions qui suivent, et achèvent la chaîne, sont rapides (un petit million d’années...), et ne posent pas de problème.
Pour être complet, il faut mentionner deux variantes du cycle proton-proton. Celle donnée ci-dessus se nomme alors PPI, et les deux autres PPII et PPIII. Elles font intervenir le lithium et le bérylium, qui sont des noyaux très fragiles, qui se brisent en général avant de pouvoir intervenir dans une autre réaction. Pour cette raison, l’efficacité de ces variantes est beaucoup plus faible que celle du cycle principal. Elles nécessitent la présence de noyaux d’hélium dans le plasma. Elles passent par des noyaux plus lourds, Bérylium 7 et même Bore 8.
Dans la variante PPII, le Bérylium se désintègre en Lithium :
| réaction | type |
|---|---|
| 3 2He + 4 2He → 7 4Be + γ | nucléaire |
| 7 4Be + e- → 7 3Li + νe | béta |
| 7 3Li + 1 1H → 4 2He + 4 2He | nucléaire |
Le 4
2He qui intervient dans la première réaction se retrouve à la fin dans la dernière. On dit qu’il a servi de catalyseur pour la réaction, par analogie avec les catalyseurs chimiques.
La seconde réaction est une désintégration béta, par capture d’un électron (négatif), qui annule la charge positive d’un proton.
Ici, le Bérylium croît encore en Bore, puis ce dernier en Bérylium 8, dont le noyau est équivalent à deux particules alpha :
| réaction | type |
|---|---|
| 3 2He + 4 2He → 7 4Be + γ | nucléaire |
| 7 4Be + 1 1H → 8 5B + γ | nucléaire |
| 8 5B → 8 4Be + e+ + νe | béta |
| 8 4Be → 4 2He + 4 2He | nucléaire |
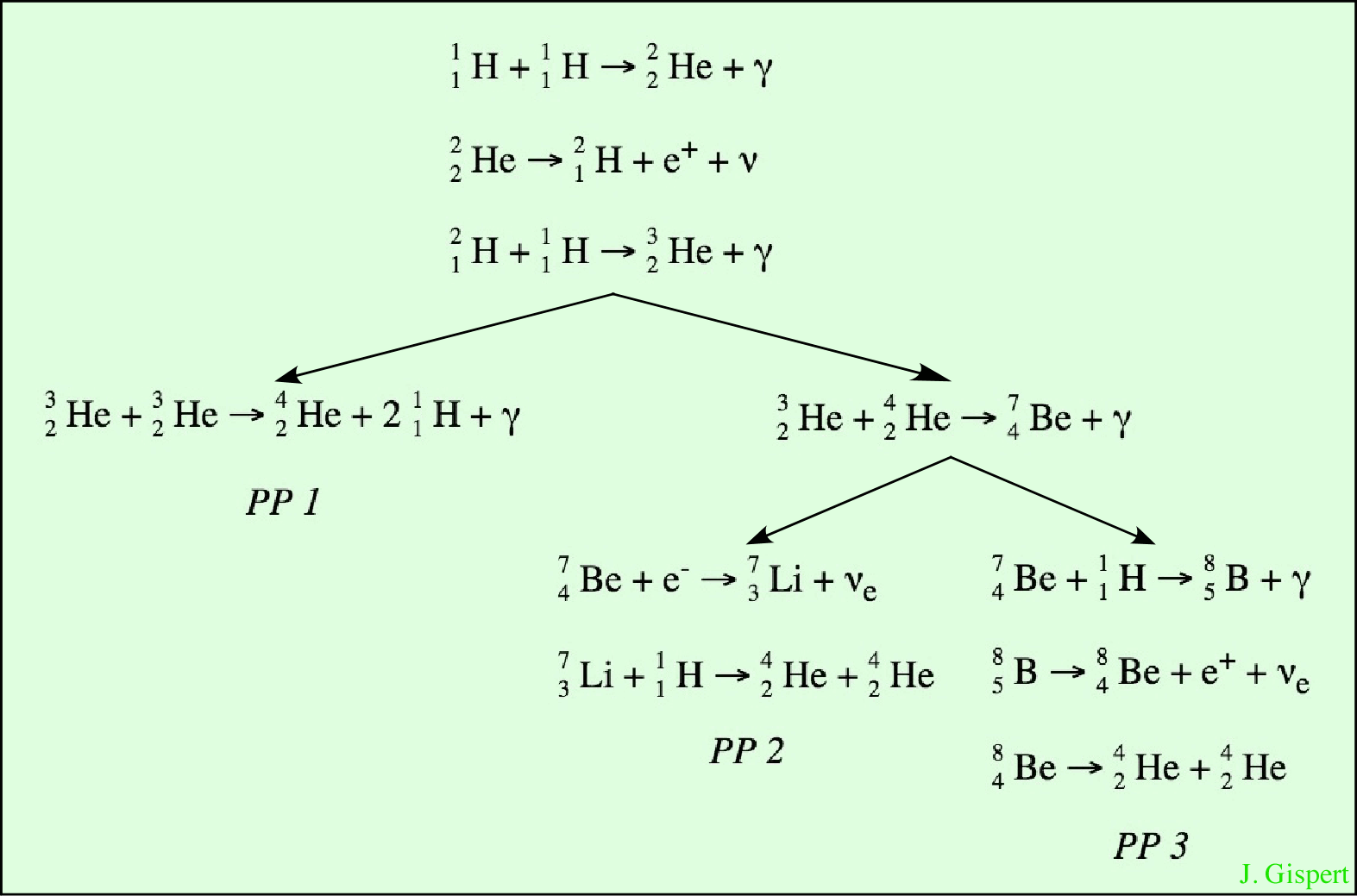
Résumé de la chaîne proton-proton
On visualise bien les différences entre les trois branches :
Une remarque à propos des deux variantes : au début de la fusion, le taux de 4
2He est très faible dans le cœur de l’étoile. Aussi, les réactions PP2 et PP3 ne se produisent-elles qu’exceptionnellement. Mais à mesure que la première chaîne concentre l’hélium, la probabilité des variantes augmente. La chaîne PP1 nécessite que deux réactions 1
1H + 1
1H se réalisent, afin de disposer de deux noyaux 3
2He. Mais les variantes n’ont besoin que d’un seul noyau 3
2He pour produire un noyau d’hélium 4. Donc, lorsque ces variantes deviennent productives, un noyau 4
2He est obtenu pour chaque fusion 1
1H + 1
1H.
On exprime le taux de production de la chaîne PP complète en fonction de la température. La formule de base est le taux de la première branche. Elle est valable à faible température, disons jusqu’à 8 millions de degrés. Pour obtenir une formule générale, on multiplie la formule de base par un terme qui représente l’apport des variantes lorsqu’elles sont actives. Ce facteur vaut 1 (il ne change pas la valeur) jusqu’à une température de l’ordre de 8 millions de degrés. Au-dessus, il augmente, pour atteindre pratiquement 2 vers 20 millions de degrés. Cette augmentation représente la contribution de la branche PP2, et s’explique par la remarque ci-dessus (un noyau 4
2He par fusion 1
1H + 1
1H). A plus haute température encore, la branche PP3 est favorisée par rapport à PP2. Mais elle produit moins d’énergie, et le taux est alors un peu décroissant.
Le cycle du carbone utilise des atomes présents dans le milieu pour permettre certaines réactions. Ces atomes servent de catalyseurs comme l’hélium dans la chaîne PP. Il ne peut donc se produire que si la métallicité de l’étoile est non nulle (si elle contient des éléments plus lourds que l’hélium). Les atomes utilisés sont reproduits à la fin du cycle, ce qui justifie la dénomination de catalyseurs.
Les deux premiers noms proviennent tout simplement des atomes catalyseurs, le seul carbone pour le premier, et les symboles chimiques des trois catalyseurs pour le second. Enfin, le denier nom provient du découvreur de ces mécanismes, Hans Bethe.
Il y a deux variantes de ce cycle. Toutes deux consistent en une succession d’absorptions de protons par un noyau de carbone (au départ). Ce noyau se transforme successivement :
Le cycle passe successivement par l’azote (7 protons), puis par l’oxygène (8 protons). La masse du noyau croissant ainsi, il devient instable, et se désintègre par radioactivité alpha, en émettant un noyau d’hélium. Le noyau d’azote 15, instable, se brise simplement en un noyau de carbone 12 (identique à celui qui a initié la réaction), et un noyau d’hélium 4 (qui vient d’être produit).
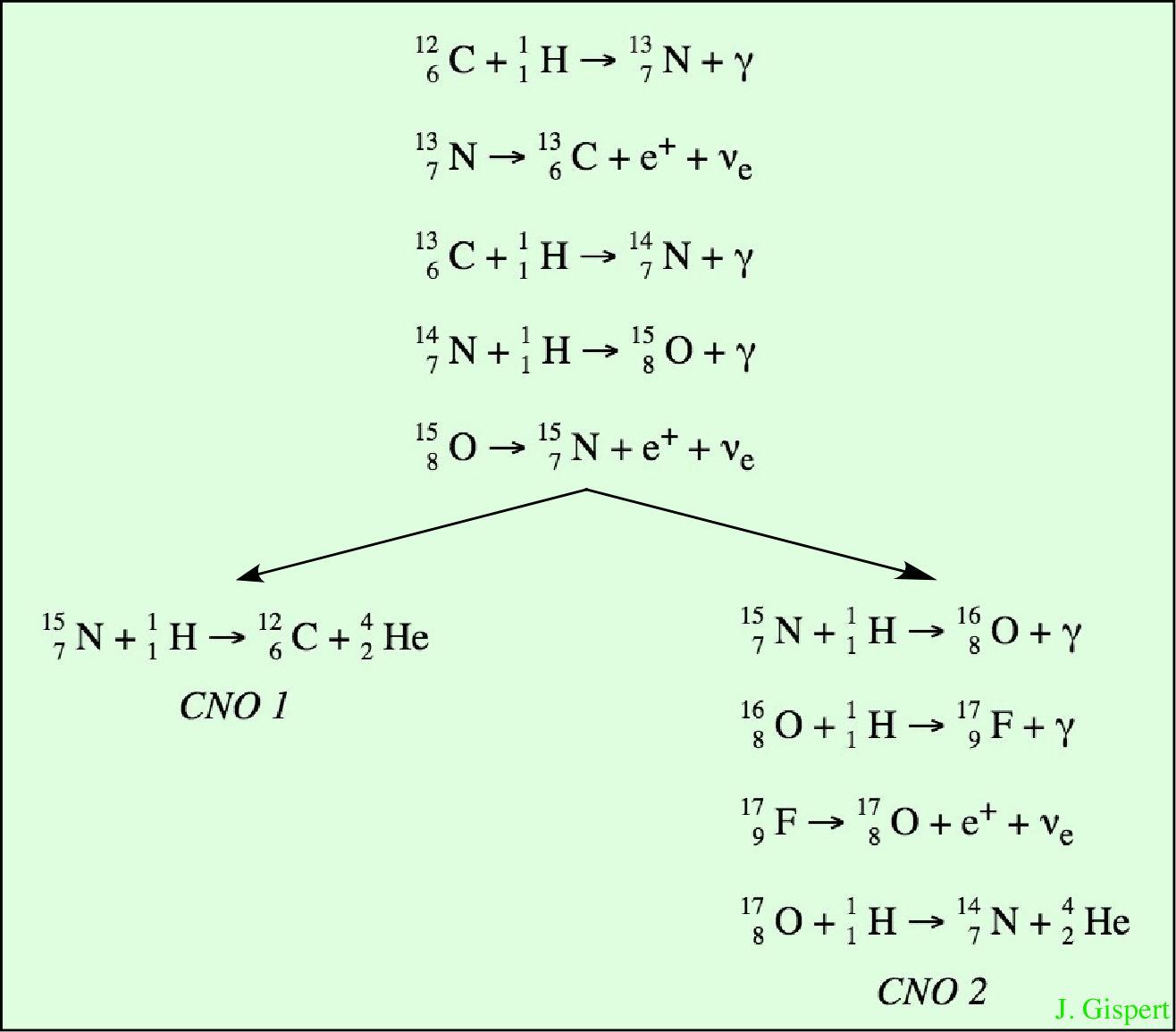
La première variante restitue le carbone utilisé dans la première réaction, alors que la seconde, passant par le fluor (9 protons) produit de l’azote dans la dernière réaction. En fait, l’azote produit peut intervenir dans la quatrième réaction du cycle, et donc redonner du carbone par la première variante au bout du compte.
Le bilan est assez difficile à faire, mais au bout du compte les abondances de carbone, azote et oxygène, ne changent guère.
Le cycle du carbone est efficace à plus haute température que la chaîne proton-proton, puisqu’il met en jeu des atomes plus lourds. A une température de l’ordre de 18 millions de degrés, les deux mécanismes produisent la même quantité d’énergie, chacun contribuant donc pour la moitié de la production totale. C’est pourquoi le moteur du Soleil, de température inférieure, est alimenté essentiellement par la chaîne proton-proton, qui produit 77 % de son énergie totale. Par contre, dans les étoiles plus massives, la température centrale est plus élevée, et le cycle de carbone devient prédominant. La masse pour laquelle ceci se produit est de l’ordre de 1,5 masses solaires.
Le schéma ci-dessous montre l’efficacité des deux cycles, et la courbe résultant de leur combinaison :
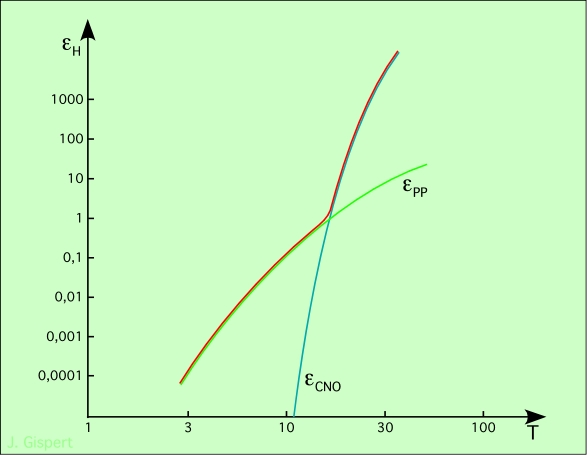
εPP est le taux de réactions de la chaîne PP, εCNO celui du cycle CNO. On voit que jusqu’à 18 millions de degrés, la courbe verte (chaîne PP) est au-dessus de la courbe bleu (CNO), et que donc la chaîne PP est plus efficace. La courbe rouge représente le taux de production d’énergie d’une étoile, qui suit le chemin le plus favorable.
Le Soleil se situe juste en-dessous du coude, et la chaîne PP y est prépondérante.
Le bilan global de toutes ces réactions peut s’écrire : 4 1
1H → 4
2He ; en effet, tout le reste est restitué à la fin de la réaction. Seul l’hydrogène a été transformé. C’est pour cette raison qu’on dit que les étoiles transforment l’hydrogène en hélium.
La fusion de l’hydrogène est le moteur de la phase la plus longue de la vie d’une étoile, la Séquence Principale. Lorsque tout l’hydrogène du cœur a été consommé, l’étoile est en panne ; mais elle peut le plus souvent utiliser un carburant de secours, tout simplement l’hélium qu’elle vient de produire. Cet élément-là est aussi capable de fusionner, mais à une température beaucoup plus élevée, qui n’était pas atteinte auparavant.
La fusion de l’hélium assure l’équilibre de l’étoile dans sa phase de géante rouge. Mais l’hélium étant plus lourd que l’hydrogène, l’énergie produite à chaque réaction est inférieure à celle produite par la fusion de 4 noyaux d’hydrogènes. Donc, pour produire une même quantité d’énergie, il faut un taux de réactions bien plus élevé. De plus, l’étoile est plus contractée, donc la gravité plus forte. Pour l’équilibrer, il faut bien plus d’énergie. Ces deux phénomènes, agissant dans le même sens, donnent une durée de vie considérablement plus courte dans la phase géante rouge, que dans la Séquence Principale.
Cette remarque est générale : plus on monte dans les masses atomiques, moins la fusion produit d’énergie. Donc les fusions successives, au cours de la vie de l’étoile, donneront de moins en moins d’énergie, et nécessiteront une température de plus en plus élevée (puisque les noyaux plus lourds ont plus de protons, la répulsion électrostatique est plus forte).
Une première idée qui vient à l’esprit pour construire des noyaux plus lourds, serait tout simplement de leur ajouter un proton. Ce genre de mécanisme a été largement utilisé dans les mécanismes précédents. Mais ce n’est pas si simple.
Il n’est pas possible d’ajouter un proton (noyau d’hydrogène) à une particule alpha (noyau d’hélium), car ceci produit un noyau de masse atomique 5. Or aucun n’est stable : 5
3Li (produit par 4
2He + p), et 5
2He (produit par la même réaction, suivie d’une désintégration béta d’un proton en neutron) ont une durée de vie de 10-21 s… C’est bien trop peu pour qu’ils capturent un autre proton et passent à Z = 6 (voir plus haut).
La particule alpha comporte deux protons, fermions identiques, qui se placent au plus bas niveau d’énergie, leurs spins antiparallèles. Ils ont ainsi des états quantiques différents. Il en est de même pour les deux neutrons.
Si on ajoute un nucléon, proton ou neutron, il devra se trouver sur le niveau d’énergie au-dessus. C’est ce qui produit l’instabilité de ces noyaux.
Pour fusionner l’hélium, il reste alors la fusion de deux particules alpha, qui donne un noyau de masse atomique 8 (donc du bérylium) :
4
2He + 4
2He → 8
4Be
Mais le Berylium 8 non plus n’est pas stable. Il se désintègre en 10-16 s. C’est très rapide, mais tout de même 100.000 fois moins que pour le lithium 5 ou l’hélium 5. En fait, dans les conditions qui règnent au centre des étoiles assez massives, les chocs entre atomes sont assez fréquents, pour que quelques atomes de 8
4Be réagissent, avant de se désintégrer, avec des particules alpha. Cette nouvelle réaction s’écrit donc :
8
4Be + 4
2He → 12
6C + γ
Ces deux réactions doivent se faire dans un temps très bref, sous peine de ne pas se réaliser du tout. C’est (presque) une réaction à trois particules alpha qui se produit. Pour cette raison, on appelle cet ensemble de deux réactions quasi-simultanées : réaction triple alpha.
Le résultat est un atome ayant le nombre de protons et de neutrons d’un atome de carbone, mais produit dans un état excité, et qui doit donc se désexciter (par réarrangement de ses nucléons). Il dispose pour cela de deux moyens :
C’est le premier mentionné des deux mécanismes qui est le plus probable. Mais les quelques désexcitations réalisées par des rayons gamma sont suffisantes pour qu’au fil du temps le carbone s’ammoncelle dans l’étoile.
La réaction de fusion de 8
4Be est donc peu probable en général, et ne justifierait pas l’abondance du carbone observée dans l’univers. Ceci a été longtemps un problème insurmontable. Il a été résolu par Edwin Salpeter dans les années 50.
La deuxième réaction, produisant l’atome de carbone, est une réaction résonante. Ceci signifie que sa section efficace (fixant le taux de réaction, comme la surface d’une cible fixe le nombre de fléchettes qui l’atteignent) dépend fortement de la température : lorsque celle-ci augmente, la section efficace croît très vite, passe par un maximum, puis décroît. Au maximum, le taux de réactions est très élevé, et l’hélium fusionne très vite en carbone. Dans certains cas, cette réaction est même explosive : c’est le flash de l’hélium, qui se produit lorsque la température, augmentant, atteint la température de résonance (parce que l’hélium est dans un état dégénéré).
Les nucléons, dans le noyau, sont organisés en couches d’énergie successives, comme les électrons dans l’atome (voir la description du modèle en couches). Chaque couche est à un niveau d’énergie. Lorsque deux noyaux fusionnent, chacun a ses nucléons organisés selon ses propres couches. Fusionnant, ils conservent la structure précédente (deux systèmes de couches). Ils produisent donc un noyau composé, dans lequel les couches ne correspondent pas au nombre total de nucléons. C’est l’origine de l’excitation.
Deux voies s’offrent pour désexciter le noyau intermédiaire : soit il éclate, et redonne les constituants de départ (c’est donc comme si rien ne s’était passé), soit le réarrangement des nucléons se produit, et un photon emporte l’énergie d’excitation. Mais la première alternative est de loin la plus probable.
Il arrive cependant, pour certaines réactions, que l’énergie d’excitation du noyau composé corresponde (presque exactement) à un niveau d’excitation du noyau ayant même nombre de protons et neutrons (mais organisés en couches). Alors, la probabilité de désexcitation par ce mécanisme est considérablement augmentée. L’énergie du noyau composé dépend évidemment de l’énergie cinétique des deux noyaux qui réagissent ; donc, elle dépend de la température du milieu. C’est ce qui explique l’existence d’une température de résonance.
Prenons l’exemple du carbone, dans la réaction
8
4Be + 4
2He → 12
6C + γ. La réaction peut se décomposer en :
8
4Be + 4
2He → Noyau Composé → 12
6C + γ
Le noyau de carbone final possède des niveaux d’énergie quantifiés. Le noyau composé, intermédiaire, contient bien 6 protons et 6 neutrons, mais ils ne sont pas arrangés pour former un noyau de carbone : il est dans un niveau d’énergie excité.
Or le noyau intermédiaire possède justement une énergie égale à celle d’un niveau excité du carbone. On dit que la réaction est résonante pour cela. Ainsi, il est tout à fait possible que le noyau intermédiaire se désexcite en passant dans l’état fondamental du carbone.
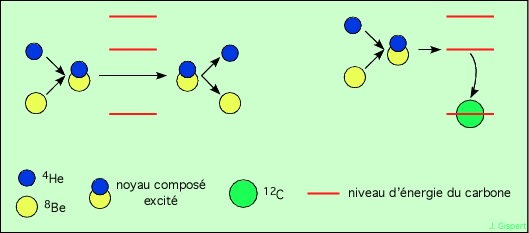
A gauche, le noyau composé possède une énergie qui ne correspond pas à un niveau de l’atome de carbone. Il se brise et redonne les deux composants séparés. A droite au contraire, son énergie est égale à celle d’un niveau excité du carbone. Alors, le noyau composé peut facilement se désexciter en émettant cette énergie (photon gamma), et se trouver donc au niveau fondamental du carbone, stable. Les nucléons, en perdant cette énergie, se réarrangent selon les couches du carbone.
Ces réactions ne sont possibles que lorsque la barrière électrostatique des protons est vaincue. Puisqu’elles mettent en jeu trois noyaux d’hélium, soit 6 protons, l’énergie cinétique des noyaux doit être très grande, et donc aussi leur température. 100 millions de degrés au moins sont nécessaire, et la densité doit être d’au moins 100 kg/cm3 pour assurer un taux de réaction suffisant. C’est pourquoi la fusion de l’hélium est impossible pendant celle de l’hydrogène (Séquence Principale).
De nombreuses autres réactions résonantes participent à l’explication du fonctionnement des étoiles, dans toutes leurs phases d’évolution. Ceci est possible parce que la température du cœur de l’étoile augmente plus ou moins rapidement, et finit ainsi par atteindre la température de résonance pour certaines réactions.
Ces deux réactions produisent 7,275 MeV par noyau de carbone produit. C’est 10 fois moins que ce que donne la fusion de l’hydrogène, par unité de masse.
Dans les mêmes conditions de température et de pression, d’autres réactions sont possibles. En réagissant avec une particule alpha, le carbone donne de l’oxygène 16. Cet oxygène peut parfois capturer une nouvelle particule alpha, pour donner du néon 20. De son côté, l’azote 14 produit de l’oxygène 18 :
Comme la réaction qui produit le carbone, ces réactions sont résonantes. Elles produisent les noyaux dans un état excité, qui se désexcite spontanément par émission d’un photon gamma.
L’azote 14 qui existe dans le milieu produit, dans les mêmes gammes de conditions et par des réactions résonantes, de l’oxygène 18 :
En fonction du taux de réalisation de chacune de ces réactions à la température considérée, on arrive à un état d’équilibre, et un mélange bien déterminé des différentes espèces produites. L’ensemble conduit à un cœur constitué de 49 % de 12
6C, 49 % de 16
8O et 2 % de 18
8O, à la fin de la fusion de l’hélium.
L’oxygène 18 est peu important en pourcentage, mais donne toute une famille de réactions, produisant beaucoup de neutrons. La première est la réaction entre un oxygène 18 et une particule alpha :
18
8O + 4
2He → 22
10Ne + γ
Elle donne du néon 22, qui peut à son tour capturer une particule alpha, donnant du magnésium. Enfin, le magnésium produit du silicium. Voici la suite de ces réactions :
| 18 8O + 4 2He → 22 10Ne + γ | 22 10Ne + 4 2He → 26 12Mg + γ | 26 12Mg + 4 2He → 29 14Si + γ |
La réaction suivante donnerait de l’argon. Mais le processus s’arrête là, car les conditions de température et de pression ne permettent pas de franchir la barrière électrostatique au-delà.
Une émission de neutron intervient parfois dans ce processus, et produit des noyaux ayant un neutron de moins, donc un isotope plus léger :
|
18 8O + 4 2He → 21 10Ne + n | 22 10Ne + 4 2He → 25 12Mg + n | 25 12Mg + 4 2He → 28 14Si + n |
Voici le résumé :
|
18 8O + 4 2He → 21 10Ne + n | 22 10Ne + 4 2He → 25 12Mg + n | 25 12Mg + 4 2He → 28 14Si + n |
| 18 8O + 4 2He → 22 10Ne + γ | 22 10Ne + 4 2He → 26 12Mg + γ | 26 12Mg + 4 2He → 29 14Si + γ |
Ces réactions produisent beaucoup de neutrons, comme on peut le voir. Ces neutrons permettront de nouvelles synthèses, par addition de neutrons (processus r et s). Elles auront un grand rôle à jouer dans certaines circonstances.
Si on s’intéresse à des noyaux plus lourds encore, on comprend bien que la température doit être de plus en plus élevée. Pour atteindre les températures requises, il faut que l’étoile ait une masse suffisante. Pour le Soleil, l’histoire s’arrêtera après la fusion de l’hélium.
Les fusions ne pourront pas se produire dans la même zone et au même moment. Ceci aura de grandes conséquences sur la constitution interne des étoiles de grande masse.
Lorsque la température atteint les 500 millions de degrés (avec efficacité maximum à 800), le carbone à son tour fusionne. Mais les réactions sont plus variées que pour la fusion de l’hydrogène. Deux atomes de carbone se combinent, pour donner du magnésium, du sodium ou du néon :
| 12 6C + 12 6C → 24 12Mg + γ |
| 12 6C + 12 6C → 23 12Mg + n + γ |
| 12 6C + 12 6C → 23 11Na + 1 1H + γ |
| 12 6C + 12 6C → 20 10Ne + 4 2He |
On y retrouve la désexcitation par émission d’un photon gamma et l’émission d’un neutron.
Ces réactions se comprennent de la façon suivante :
Remarquez que le noyau de néon produit est l’isotope 20, alors que les réactions précédentes donnaient les isotopes 21 et 22.
La deuxième réaction, qui produit le magnésium 23, est endothermique, c’est-à-dire qu’elle consomme de l’énergie au lieu d’en produire. Ces réactions produisent normalement de l’énergie, qui combat l’effondrement gravitationnel de l’étoile. Si de nombreuses réactions comme celle-ci se produisent, au lieu de le combattre, elles accéléreront l’effondrement. En plus, les neutrinos produits dans certaines réactions traversent la matière de l’étoile sans interaction, donc sans y déposer leur énergie. Ils emportent ainsi presque 30 % de l’énergie produite par l’étoile dans cette phase.
Enfin, le néon et le sodium produits donnent du magnésium, noyau le plus stable de cette zone de masse, et donc le plus abondant à la fin des réactions.
| 20 10Ne + 4 2He → 24 12Mg + γ |
23 11Na + p → 24 12Mg + γ |
La fusion de l’oxygène devient possible à des températures encore plus élevées, de l’ordre du milliard de degrés. Ce qui nécessite une étoile de masse importante pour atteindre une telle température.
| 16 8O + 16 8O → 32 16S + γ |
| 16 8O + 16 8O → 31 16S + n |
| 16 8O + 16 8O → 31 15P + p |
| 16 8O + 16 8O → 28 14Si + 4 2He |
| 16 8O + 16 8O → 24 12Mg + 2 4 2He |
Les mécanismes sont les mêmes que ci-dessus. La seule différence est dans la dernière réaction, qui éjecte deux particules alpha. Parmi les produits de ces réactions, le silicium est le plus stable. C’est donc lui qui est le plus abondant à la fin des réactions.
Le silicium 28 produit ci-dessus donne, par capture d’une particule alpha, du soufre 32, qui vient s’ajouter à celui déjà produit :
28
14Si + 4
2He → 32
16S + γ
Par photodésintégration, des atomes de silicium 28 éjectent une particule alpha, produisant du magnésium 24 (seconde voie de production) :
28
14Si + γ → 24
12Mg + 4
2He
La fusion du silicium requiers une température de 4,5 milliards de degrés pour se produire, en franchissant la barrière coulombienne de répulsion électrique. Ceci pose un gros problème : avant d’atteindre de telles températures, le rayonnement de corps noir devient tel que des photons gamma sont émis en abondance (ils emportent une partie de l’énergie). Ces photons sont assez énergétiques pour briser de nombreux atomes, et produisent des réactions de désintégration. En effet, leur énergie est du même ordre de grandeur que les niveaux excités des atomes. Plutôt que de se construire, les noyaux vont donc se briser. Ce phénomène empêche la fusion des éléments à partir du silicium (la fusion est la réaction d’un élément sur lui-même).
Les noyaux les plus fragiles sont brisés les premiers : ce sont ceux dont la masse atomique est impaire. Le fer et le silicium, de masse atomique paire, sont pour l’instant préservés. Ceci explique en partie le pic du fer.
Le pic du fer est une abondance plus forte du fer que des éléments de masses voisines. Ceci ne peut s’expliquer que par une stabilité particulière du fer, plus importante que celle des noyaux proches.
Le pic du fer s’explique par des réactions d’équilibre. Certaines réactions produisent un noyau instable, qui se désintègre très rapidement. Mais si de nombreuses réactions de ce type se produisent à chaque seconde, elles peuvent maintenir un faible taux du noyau instable avant qu’il ne se désintègre.
Le fer, étant l’élément le plus stable, bloque les réactions de fusion. Puisqu’au début de l’univers il n’y avait que de l’hydrogène et de l’hélium (plus des traces de deutérium et de lithium), les éléments plus lourds que le fer n’ont trouvé jusqu’ici aucune explication. Nous allons voir maintenant des mécanismes nouveaux, qui permettent de les synthétiser, dans des circonstances particulières.
Les réactions d’addition de neutrons ne jouent pas de rôle important dans la Séquence Principale, mais deviennent essentielles dans quelques cas où les neutrons sont émis en grandes quantités. Elles expliquent la formation des éléments à partir d’une masse atomique de 65 (que le fonctionnement des étoiles n’explique pas, tout au moins dans les proportions observées).
Pourquoi les noyaux ne peuvent-ils pas avoir un nombre très grand de neutrons ? La répulsion électrostatique ne l’explique pas, étant donnée leur neutralité. La raison tient dans le principe d’exclusion : pour un nombre de protons donné, plus on met de neutrons, plus ils seront proches les uns des autres. On serait alors amené à avoir deux neutrons (deux fermions identiques), au même endroit. Le principe de Pauli ne le permet que s’ils sont de spins opposés, et par conséquent on ne peut en mettre que deux ayant la même énergie, c’est-à-dire la même vitesse (nulle). Si un troisième arrive, il sera animé d’une vitesse qui ne lui permettra pas de rester lié.
Dans les phases normales de vie d’une étoile, la production de neutrons est faible, ne permettant ces processus qu’à un taux dérisoire. Mais pendant certaines phases transitoires, le taux de production des neutrons peut être conséquent.
Un atome qui a ainsi absorbé un neutron conserve le même nombre de protons, donc il s’agit toujours du même élément chimique. Mais on est en présence d’un isotope plus lourd. Est-il stable ?
Les processus r et s sont des processus d’addition de neutrons. Lorsqu’on ajoute un neutron à un noyau, on peut obtenir un nouveau noyau stable ou instable. Et s’il est instable, il se désintègre plus ou moins vite.
Naturellement, ce mécanisme produit des noyaux trop riches en neutrons, qui devront se désintégrer soit par réaction béta, soit par émission d’une particule. L’addition de neutrons, alternée avec des désintégrations béta ou des émissions de particules, permet toute une cascade de réactions qui produisent de nombreux éléments et isotopes.
Les réactions de spallation sont produites sur un noyau lourd (relativement), par l’impact d’une particule comme un proton ou une particule alpha. Ce choc perturbe l’équilibre du noyau percuté, et peut en extraire des fragments, particules simples ou noyaux légers. Parfois, elle peut induire la fission du noyau en deux noyaux de masses semblables. L’énergie typique de la particule incidente est de 200 MeV à 3 GeV.
Les réactions de spallation produisent des isotopes qui ne sont pas obtenus par des réactions d’addition.
Une réaction de spallation importante produit du lithium, qu’on ne sait obtenir différemment :
12
6C + p → 7
3Li + 4
2He + 2 p
Le proton incident pénètre dans le noyau. Il bouscule les nucléons (cascade intra-nucléaire), et provoque l’éjection de la particule alpha, et d’un autre proton. Cette phase dure de 10-23 à 10-21 seconde ! C’est le temps que met le proton incident à se déplacer dans le noyau, à une vitesse proche de celle de la lumière.
Le diamètre du noyau est de l’ordre de d = 10-15 m. Supposons qu’il soit parcouru à la vitesse de la lumière :
la distance parcourue est d = c t
le temps de parcours est donc : t = d / c
soit t = 10-15 m / 300.000.000 m/s = 1/3 10-15 10-8 = 1/3 10-23 s
Si le proton incident est 100 fois moins rapide que la vitesse de la lumière, on obtient 10-21 s. Si le proton incident est moins rapide, il n’a pas l’énergie suffisante pour provoquer la spallation.
Lorsque les particules ont été éjectées, le noyau restant est fortement perturbé, ses nucléons ne sont pas en équilibre. Ils se réarrangent progressivement, en un temps bien plus long, de l’ordre de 10-16. C’est la désexcitation.
La spallation étant un jeu de quilles, un neutron, sans charge électrique, peut aussi la produire.
Quelles sont les avancées faites en astronomie par la connaissance des réactions nucléaires ?
Elles sont de plusieurs ordres, selon le point de vue :
Lors de la séquence principale, l’énergie est produite par la fusion de l’hydrogène ; pendant la phase géante rouge, c’est la fusion de l’hélium, produit pendant la séquence principale, qui prend le relais ; ensuite, la fusion du carbone, puis de l’oxygène, du silicium, achèvent de contenir la gravité. Ce qui se passe ensuite dépend de la masse de l’étoile considérée, mais plus aucun équilibre ne peut venir d’une production d’énergie. La pression quantique de Fermi assure un équilibre définitif dans les naines blanches (par les électrons), et dans les étoiles à neutrons (par les neutrons), car elle ne nécessite aucune énergie.
Les éléments constitutifs de la matière interstellaire et des nuages de gaz sont produits par :
Dans la nature, on ne connait pas d’élément plus lourd que l’uranium, qui possède 92 protons. Chacun sait que certains des isotopes de l’uranium sont radioactifs, ce sont ceux qui permettent de retirer de l’énergie des centrales nucléaires actuelles.
Les noyaux ayant certains nombres particuliers de protons ou de neutrons présentent une stabilité particulièrement élevée. Ceci est expliqué par le modèle en couches du noyau atomique. Les abondances observées des éléments chimiques s’expliquent en partie par ce modèle de noyau.
La vallée de stabilité des noyaux atomiques
animation réalisée par Animéa pour le CEA (Irfu) et GANIL
Certaines particules sont stables, d’autres se désintègrent spontanément. On a tenté de mesurer la durée de vie du proton, sans succès. Il semble vraiment très stable, au point que sa durée de vie est supérieure à 1031 ans. L’âge actuel de l’Univers est de l’ordre de 10 milliards d’années, i.e. 1010 ans. Le proton doit donc vivre au moins 1021 fois l’âge de l’Univers…
Par contre, le neutron est instable, mais seulement dans son état libre. Sa durée de vie est de 10,6 minutes. Dans l’état lié, il est stable, fort heureusement, sinon les atomes n’existeraient pas !
La fission n’intervient pas dans les étoiles, qui tirent leur énergie de la fusion des éléments jusqu’au fer. Mais elle se produit dans certaines circonstances très particulières, comme par exemple le maintien de l’éclat d’une supernova, après l’explosion. Pendant la phase explosive elle-même, la température et la densité sont assez élevées pour synthétiser des éléments plus lourds que le fer, parce qu’il y a énormément d’énergie disponible, produite en un temps très bref. Cette énergie ne demande qu’à être utilisée, alors que dans les étoiles, elle doit servir à maintenir l’équilibre… Parmi les éléments produits dans l’explosion, certains sont radioactifs, avec des périodes diverses. La courbe de lumière montre bien la décroissance radioactive des éléments à courte période concernés.
La fission est la rupture spontanée d’un noyau lourd, trop massif pour être stable, en noyaux plus légers. C’est ce qui se produit s’il possède trop de nucléons, car l’interaction forte s’affaiblit très vite avec la distance (elle a une portée très faible). Lorsque le noyau contient un grand nombre de nucléons, la distance entre deux nucléons augmente, et donc l’interaction forte diminue rapidement. Mais la répulsion électrostatique entre les protons diminue bien moins vite, et finit par devenir prépondérante. Alors, le noyau perd sa cohésion, et va à la rupture.
Prenons l’exemple de l’uranium 235 (98 protons + 137 neutrons). Ce noyau est instable, car la liaison entre ses nucléons est faible, et la répulsion coulombienne presque aussi intense que l’attraction. Il présente une fission spontanée : chaque atome d’uranium 235 a une probabilité de se désintégrer très faible. On caractérise cette désintégration en indiquant le temps au bout duquel il ne reste plus que la moitié d’une masse initiale. Pour l’uranium 235, elle est de 700 millions d’années. Il s’use même si on ne s’en sert pas, mais pas vite
La fission de l’uranium produit une particule alpha (noyau d’hélium) et de l’énergie. Ceci parce que la particule alpha (deux protons et deux neutrons) ne présente qu’une faible répulsion électrostatique, produite par l’intéraction entre ses deux protons, et une attraction importante due à l’interaction forte entre ses 4 nucléons. La structure très symétrique de l’assemblage augmente encore sa cohésion. Pour l’atome d’uranium instable, il est donc plus facile de se défaire d’une particule alpha que d’un simple proton par exemple.
La fission de l’uranium est utilisée dans les centrales nucléaires. Ceci n’intéresse pas directement l’astronomie, bien que la désintégration des noyaux d’uranium à l’intérieur de la Terre (et des autres planètes) produit de la chaleur, sans laquelle notre planète serait sans doute froide aujourd’hui, et ne présenterait plus aucune activité volcanique ou tectonique. La Lune, Mercure et Mars, beaucoup plus petites, n’ont plus cette source pour les maintenir.
L’uranium 235 est faiblement fissile, c’est-à-dire qu’il se brise spontanément, mais avec une probabilité faible. Mais s’il est frappé par un neutron, la fission est provoquée :
Lorsqu’un noyau d’uranium reçoit un neutron (qui peut s’approcher sans subir de répulsion coulombienne), il se transforme en un autre isotope, l’uranium 236 (98 protons + 138 neutrons).
235
92U + n → 236
92U
Cet isotope est produit dans un état excité. Dans 16 % des cas, il se désexcite par rayonnement électromagnétique, et l’arrangement des nucléons devient stable. Sinon, il se désintègre en deux atomes de masse moyenne, et quelques neutrons. Le nombre de neutrons dépend des deux atomes produits, car plusieurs réactions différentes sont possibles :
236
92U → 92
36Kr + 141
56Ba + 3 n
236
92U → 93
36Kr + 140
56Ba + 3 n
236
92U → 94
38Sr + 140
54Xe + 2 n + γ
… et d’autres encore. Ces réactions n’ont pas toutes la même probabilité de se produire. Si on considère un grand nombre d’atomes d’uranium 235, les désintégrations produisent en moyenne 2,47 neutrons par atome brisé.
Imaginez qu’on possède une masse d’un kilo d’uranium 235. Dans cette masse, un atome se désintègre spontanément, en émettant deux neutrons (par exemple). Ces neutrons vont heurter deux autres atomes de l’uranium, qui vont se briser par la réaction ci-dessus, en émettant 3 nouveaux neutrons, qui vont à leur tour… Ce phénomène prend le nom de réaction en chaîne. En un temps extrêmement bref, tous les noyaux d’uranium vont éclater, et chacun libère son énergie. La quantité d’énergie libérée est vraiment énorme, et puisque c’est en un temps très bref, c’est une explosion : c’est le principe de la bombe A. Les fissions spontanées étant rares, la réaction en chaîne ne se déclenche que s’il y a un nombre suffisant d’atomes : c’est la masse critique.
Bien d’autres atomes se désintègrent ainsi, et leurs propriétés sont extrêmement utiles. C’est pourquoi il faut les étudier.
Des désintégrations se produisent dans les planétoïdes lorsqu’ils viennent juste de se former, et participent activement à leur chauffage, qui va permettre la différenciation. Il s’agit là d’atomes qui se désintègrent rapidement, on dira qu’ils sont à courte période.
Mais les désintégrations ont aussi un usage très important en astronomie, car ce sont elles qui permettent de donner des dates ! On utilise pour cela une propriété fondamentale : le taux de désintégration est constant, et ne dépend pas des conditions physiques dans lesquelles se trouvent les atomes. On peut mesurer ces taux en laboratoire, et ensuite, la proportion d’atomes radioactifs que l’on trouve dans un échantillon permet de déduire son âge.
La désintégration radioactive obéit à un double principe. Dans le temps (infinitésimal) dt :
Ceci implique que le nombre N d’atomes restant à l’instant t après la formation des atomes est :
N = N0 e-log 2 t / T
Au bout du temps T, il reste la moitié des atomes initiaux. Au bout de 2 périodes (2 T), il en reste le quart. Au bout de 3 périodes, il n’en reste plus que le huitième…
| Période | Nouvel échantillon |
Désintégration radioactive d’un élément de période donnée.
Les atomes sont représentés par des points rouges, qui passent au jaune lorsque l’atome se désintègre. On remarque que les désintégrations sont très nombreuses au début, puis se ralentissent. Lorsqu’il ne reste que peu d’atomes radioactifs, les désintégrations sont bien plus rares. Ceci parce que le nombre de désintégrations par unité de temps (par seconde), est proportionnel au nombre d’atomes radioactifs présents. La décroissance est donc exponentielle, et la courbe à droite est construite en reportant à chaque trame le nombre d’atomes radioactifs restant.
La période est modifiable par action sur le curseur. Pour que l’animation soit utilisable, les périodes sont limitées à un domaine réduit, de 50 à 500 unités de temps. Cette unité est arbitraire, l’important est de visualiser la vitesse décroissante de la désintégration. Au bout d’une période, il reste la moitié des atomes ; au bout d’une seconde période, il en restera seulement le quart... Au bout de 10 périodes, il n’en restera qu’un peu moins d’un millème. Ainsi, les éléments radioactifs à courte période ne subsistent que relativement peu de temps après leur synthèse. D’un kilogramme de carbone 14, dont la période est de 5 730 ans, il ne reste qu’un gramme au bout de 10 périodes, soit 57 000 ans.
Le bouton de droite permet de créer un nouvel échantillon, avec la période fixée par le curseur.
La barre de progression, en haut à gauche, visualise la proportion d’atomes radioactifs par rapport au nombre d’atomes initial. De 100 % au départ, elle arrive donc à 0 %. Observez la vitesse de son évolution, très rapide au début (lorqu’il y a beaucoup d’atomes radioactifs), puis de plus en lente (le nombre d’atomes radioactifs restant étant de plus en plus faible).
Désintégration radioactive de certains éléments, dans les planètes, dans les supernovæ…
La désintégration radioactive demande la présence d’atomes lourds, susceptibles de se briser. Il faut donc qu’ils aient été créés par un mécanisme précédent (essentiellement réactions explosives). Les principaux radioéléments sont l’uranium, le potassium 40, le thorium, et l’aluminium. Ils jouent des rôles différents, en fonction de leur mécanisme de formation et de leurs périodes.
Ces différents mécanismes sont étudiés dans les chapitres correspondant aux domaines où ils interviennent.
Les éléments à longue période ont un rôle majeur dans l’entretien de la chaleur d’une planète. Normalement, celles-ci sont chauffées par accrétion et contraction gravitationnelle dans leur phase de formation, mécanismes qui cessent rapidement. Ensuite, elles ne peuvent plus que se refroidir progressivement dans l’espace. Mais la présence d’éléments radioactifs en leur sein, par l’énergie dégagée lors de la fission, entretient un flux de chaleur qui compense partiellement le refroidissement.
Cette production d’énergie a sa source dans la masse de la planète, donc dans son volume. Elle est par conséquent proportionnelle au cube du rayon. De l’autre côté, le refroidissement se fait par la surface, donc proportionnellement au carré du rayon. Le bilan énergétique (gain / perte) est donc proportionnel au rapport R3 / R2 = R. Une planète conserve donc sa chaleur d’autant plus facilement qu’elle est plus grosse (rayon plus grand). C’est ce qui explique que Mercure et Mars soient refroidies, alors que la Terre est encore active (volcanisme).
L’explosion d’une supernova est un phénomène bref. La luminosité devrait donc monter très rapidement (ce qu’elle fait), puis baisser presque aussi vite. Or la baisse est beaucoup plus lente. On explique ce retard par la désintégration d’un isotope de l’aluminium, 26
13Al, dont la période est brève, et qui est synthétisé lors de l’explosion. L’explosion passée, l’aluminium 26 commence à se désintégrer, produisant une énergie qui va entretenir assez longtemps l’éclat de la supernova. Vous trouverez des explications détaillées dans le chapitre correspondant.
Le diagramme de Segrè, daté de 1945, dérive d’un ancêtre dû à Giorgio Fea. Depuis, des évolutions ont été proposées, mais le principe reste le même : il s’agit de classer graphiquement les noyaux atomiques connus selon deux axes, portant le nombre de protons (abscisse) et le nombre de neutrons (ordonnée). Si les noyaux avaient même nombre de protons et de neutrons, ils seraient sur la diagonale. Si ceci est assez vérifié pour les noyaux légers, les plus lourds contiennent davantage de neutrons, et sont donc au-dessous de la diagonale.
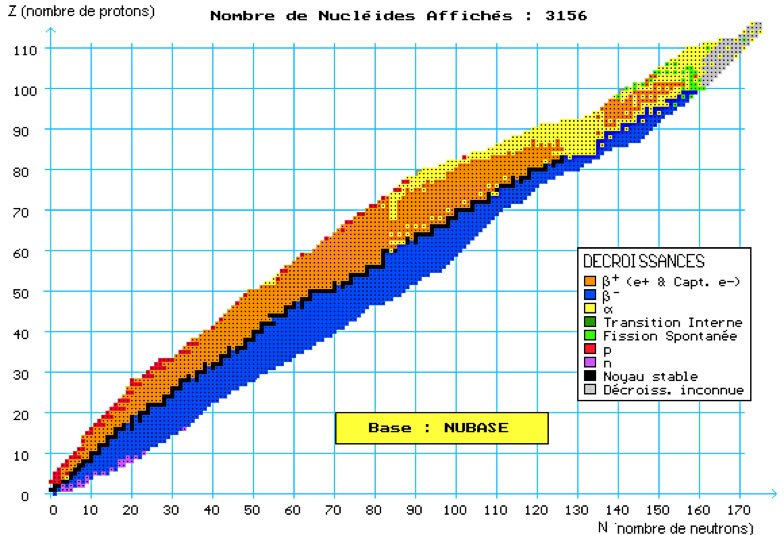
Beaucoup d’information se trouve dans ce diagramme. La légende des couleurs indique les différents modes de désintégration, associée à chaque noyau.
Le plus important pour nous, qui concerne les atomes dont nous sommes faits, est donné par les noyaux figurés en noir, selon la ligne principale du diagramme. Ce sont les noyaux stables. Tous les autres sont radioactifs, mais les modes de décroissance sont variés.
Supposons qu’on ait un échantillon contenant N atomes, dont p sont radioactifs, et les N - p autres proviennent de la désintégration. Au moment de la formation de l’échantillon, tous les atomes étaient radioactifs, il y en avait donc N. Puisqu’il y en reste maintenant p de radioactif, on peut écrire :
p = N e-(log 2) t / T
La période T est connue, et on mesure p. On peut donc calculer t :
p / N = e-(log 2) t / T
log(p / N) = -(log 2) t / T
t = -log(p / N) / (T log 2)
On obtient donc t en fonction de N. Il suffit de connaître N pour avoir la valeur de t.
Les arbres utilisent le gaz carbonique de l’atmosphère pour produire le bois, qui contient donc cette proportion de C 14. A la mort de l’arbre, ce C 14 commence à se désintégrer. Si on mesure la proportion qu’il reste aujourd’hui, on peut en déduire depuis combien de temps l’arbre est mort.
Cette méthode de datation s’adapte aux périodes peu anciennes qui concernent l’archéologie, car la période du carbone 14 n’est que de 5.734 ans. Au bout de 7 périodes, il ne reste que 1 / 27 = 1 / 128e de la quantité initiale. La méthode permet donc de dater jusqu’à 40.000 ans à peu près.
Avec des éléments de période plus longue, on peut dater des échantillons bien plus anciens. La méthode Potassium-Argon (le Potassium 40 se désintègre en Argon 40) est adaptée à des durées beaucoup plus longues, sa période étant de 1,25 milliards d’années.
En astronomie, on utilise d’autres atomes instables pour dater par exemple les météorites.
On trouve dans la nature tous les isotopes des éléments produits soit lors de la nucléosynthèse primordiale, soit dans les étoiles, soit par des réactions de spallation ou d’addition de neutrons sur des noyaux existants. Certains noyaux produits naturellement sont radioactifs, et disparaissent au cours du temps, plus ou moins vite. Les plus instables ont disparu depuis longtemps, sauf s’ils sont produits en permanence (C 14). Ceux à longue période sont encore présents, leur abondance étant directement liée à leur période.
Mais certains isotopes ne sont pas produits naturellement. Les moyens dont on dispose aujourd’hui permettent de compléter cette panoplie naturelle. C’est ainsi qu’en bombardant des noyaux assez lourds par des noyaux de masse moyenne, on peut obtenir des noyaux plus lourds que tout ce qui existe naturellement (au-delà de z = 92, bien qu’on ait observé un peu de californium z = 98, dans l’espace interstellaire). Dans certains cas, on n’a produit qu’un seul noyau… De plus, ces éléments sont instables et se désintègrent très vite.
Evidemment, ils n’ont pas de nom usuel, comme le zinc ou le fer. Il a fallu se mettre d’accord pour leur en trouver. Pour nommer un nouvel élément, l’organisme responsable attend d’avoir des indications sérieuses sur sa réalité. Aussi a-t-il décidé de donner à certains des noms provisoires, en attendant des preuves, ou même une première détection. On peut en effet établir théoriquement jusqu’où le tableau de Mendéléev pourrait aller, avec des noyaux à vie brève mais non nulle. Et ce sont ces éléments-là qu’on désigne par un nom provisoire.
Ces noms ont été définis à partir de l’élément 111, et leur construction suit une règle simple : elle est latine, et indique simplement la suite des trois chiffres qui composent le numéro, avec le suffixe ium, pour donner une allure connue ! Ainsi, l’élément 111 a été nommé Un-Un-Un, c’est-à-dire unununium. Le numéro 112 suivant est ununbium. Puis viennent ununtrium, ununquatrium, ununpentium, ununhexium, ununseptium, ununoctium, ununennium. Pour passer à la dizaine suivante, on change le second un en bi : unbinillium (120), unbiunium, etc.
Vous remarquerez que dans le tableau, certains de ces noms fabriqués ont déjà disparu, les élément correspondant étant maintenant acceptés, et ayant reçu un nom définitif.
L’élément 112 a été synthétisé pour la première fois en 1996 à Darmstadt, en Allemagne. Un seul atome a été produit ! La réaction qui l’a obtenu est la suivante :
On voit qu’il a été produit par coalescence de deux noyaux plus légers, du plomb et du zinc, dans un accélérateur d’ions lourds. La collision produit un noyau composé excité (ce qu’indique l’étoile placée à côté du symbole). Ce noyau s’est enfin désexcité en éjectant un neutron.
Lorsque sa découverte a été confirmée, on lui a donné un nom provisoire. Puisqu’il contient 112 protons, il a été nommé Unumbium (Uub).
Le nom définitif, proposé par l’équipe de Darmstadt, a été adopté par l’IUPAC le 19 février 2010, 537e anniversare de la naissance de Copernic.
Le Copernicium a plusieurs isotopes, mais aucun n’est stable. Leur nombre de masse est compris entre 277 et 285. Le plus stable a une période de 5 minutes. Ceci ne rend pas son étude bien facile. Aussi, ses propriétés sont déterminées autant par la théorie que par l’observation. On a ainsi déterminé qu’il s’agit d’un métal de transition, et qu’à température normale il est gazeux ! C’est le seul métal gazeux à température ambiante.
Même acceptés, ces éléments restent très mal connus, et leurs propriétés chimiques sont indéterminées. On pourrait se baser sur la périodicité du tableau de Mendéléev, mais ceci ne donnerait pas de bons résultats. Le nombre d’électrons est si grand, que des calculs quantiques (évidemment approchés), montrent qu’il doit y avoir des phénomènes d’interaction qui perturbent beaucoup leur ordonance, et devraient donner à ces éléments des propriétés chimiques bien différentes de ce qu’on connait. Dommage qu’ils soient si instables…
Dans la nucléosynthèse, le lithium apparaît comme un cas particulier. Il est en effet très fragile, et se détruit bien avant que la température n’atteigne la limite de fusion de l’hydrogène. Autant dire qu’il ne peut se trouver dans le cœur des étoiles.
Après le Big Bang, lorsque la température a baissé, se sont produits l’hydrogène et l’hélium primordiaux, mais aussi un peu de lithium. Comment s’est-il synthétisé, avec une telle fragilité ? Pour répondre, nous devons examiner deux pistes intéressantes :
La première est donnée par l’hélium 3. Réagissant avec une particule alpha, il produit du bérylium 7 :
3
2He + 4
2He → 7
4Be + γ
La température du milieu doit être assez élevée pour que cette réaction soit possible. Ensuite, le bérylium peut subir une désintégration béta :
7
4Be + e- → 7
3Li + νe
Le problème vient de l’avidité du lithium 7 pour capturer un proton, et se transformer en bérylium 8 !
Pour que du lithium soit effectivement produit ainsi, il faut qu’entre la synthèse du Be 7 et sa désintégration béta, la température ait suffisamment chuté pour le lithium ne puisse être détruit. Dans les conditions normales à l’intérieur des étoiles, ceci n’est pas possible, et le lithium ne peut donc être produit.
On nomme mécanisme de Cameron-Fowler la première de ces réactions (synthèse de Be 7), suivie d’un transport rapide vers un milieu plus froid, et enfin de la seconde réaction.
La seconde possibilité provient des réactions de spallation.
La recherche de la fusion controllée vise à produire énormément d’énergie dans un volume très petit, pour remplacer les énormes machines utilisées à l’heure actuelle (barrages, centrales thermiques…). L’étude des réactions de fusion dans les étoiles a montré la difficulté de réalisation de cette idée. En fait, on ne cherche même pas à reproduire ce qu’il se passe dans le Soleil. On peut dire, pour faire simple, qu’on cherche plutôt à imiter une naine brune. En effet, plutôt que de partir d’atomes d’hydrogène, dont la répulsion électrostatique est trop importante pour être envisageable, on essaye de fusionner des isotopes de l’hydrogène : deutérium et tritium.
Les réactions possibles sont :
| 2 1H + 2 1H → 3 2He + n | fusion de deux noyaux de deutérium |
| 2 1H + 2 1H → 3 1H + p | fusion de deux noyaux de deutérium |
| 2 1H + 3 1H → 4 2He + n | fusion d’un noyau de deutérium et d’un noyau de tritium |
| 2 1H + 3 2He → 4 2He + p | fusion d’un noyau de deutérium et d’un noyau d’hélium 3 |