L’actualité du LAM	Le cours à l’Observatoire Historique de Marseille	… …	liens - alphabet grec bibliographie fiches lexique multiplicateurs tableau périodique	Mis à jour le 16/10/23
Les étoiles

1 Définition

1.1 Qu’est-ce qu’une étoile ?

Un petit point lumineux qui brille dans le ciel la nuit !

Si on cherche à aller au-delà des apparences, de nombreux problèmes se posent. D’abord, on peut utiliser un instrument d’optique puissant pour tenter de mieux les voir. Espoir vite déçu : dans un instrument plus puissant, les points lumineux des étoiles apparaissent plus brillants, mais plus petits ! Ceci pour deux causes différentes :

•  les étoiles sont si loin qu’on ne peut rien voir de leur surface même avec les meilleurs télescopes (ceci est heureusement en train de changer…) ;
•  les propriétés de la lumière expliquent la plus petite taille d’un point lumineux dans un grand instrument.

L’aspect ponctuel des étoiles dans les plus grands instruments a longtemps limité leur étude à des dénombrements et des statistiques. Nous verrons plus loin que ces méthodes ont permis de concevoir la forme de notre galaxie.

Pour étudier les étoiles, il faut donc utiliser d’autres techniques, plus évoluées que le simple regard. Il faut des instruments de mesure.

Dans ce chapitre, nous allons voir ce que sont les étoiles, comment elles fonctionnent, comment elles se forment et évoluent, de leur naissance à leur mort. A côté des calmes étoiles normales, nous verrons quelques monstres, par leur taille, par leur masse, ou par leur densité. Nous verrons aussi que certaines montrent des variations d’éclat, et nous aborderons les relations qu’elles entretiennent entre elles.

Avant d’aller plus loin, nous devons préciser un point de vocabulaire très important. Nous verrons que les étoiles sont diverses, mais qu’un classement est possible. Presque toutes les étoiles qu’on voit à l’œil nu partagent un même fonctionnement, et pour cette raison on les met dans un même ensemble qu’on appelle séquence principale. Tout ceci sera détaillé plus loin.

2 Les apparences

2.1 Les constellations

Lorsqu’on regarde le ciel étoilé, certains dessins nous sautent aux yeux ; on appelle ces figures formées par les étoiles des astérismes (du latin aster). Les astérismes les plus remarquables sont nommés constellations.

Le ciel est comme un paysage : pour pouvoir en parler, il faut avoir des repères. Les constellations jouent ce rôle, depuis la nuit des temps. Un bon observateur se doit de bien connaître le ciel.

La plus belle de toutes les constellations est sans doute Orion, qui orne les nuits d’hiver. Elle est remarquable car elle est constituée d’étoiles qui sont toutes brillantes, alors que la plupart des autres constellations possèdent une ou deux étoiles brillantes, et d’autres plus discrètes.

Des constellations ont été définies par tous les peuples. Les associations les plus évidentes se retrouvent partout, parfois avec des noms différents : la Grande Ourse se nomme le Chameau chez les Touaregs. Chez les Arabes, elle évoque un corbillard.

Les constellations sont des figures formées par la perspective. Orion, par exemple, associe des étoiles très proches de la Terre, et peu brillantes, à des étoiles beaucoup plus lointaines et très lumineuses. Ces figures n’ont donc aucun intérêt astronomique, hormis celui de constituer des repères simples dans le ciel, car elles n’ont pas d’existence physique.

Les noms des constellations sont d’inspiration différente dans les deux hémisphères, pour des raisons historiques. Dans l’hémisphère nord, on trouve :

•  des noms de personnages mythologiques : Persée, Céphée, Andromède…
•  des noms d’animaux ayant eu un rôle dans la mythologie  : la Baleine, la Grande et la Petite Ourse, Pégase…
•  les noms des constellations zodiacales, qui ont une origine différente : la Vierge, le Verseau, le Capricorne, la Balance…

Les Arabes ont conservé les résultats de l’astronomie grecque, et ont fini par adopter les constellations définies par les grecs, en abandonnant les leurs. De ce fait, les noms des constellations sont, pour l’hémisphère nord, d’origine grecque, alors que les noms des étoiles sont pour la plupart d’origine arabe.

De nombreux personnages mythologiques ont été envoyés dans le ciel par les dieux pour les récompenser d’actes héroïques, ou bien les mettre à l’abri… Cette opération s’appelle la catastérisation ! Ce qui signifie transformation en astérisme.

2.2 Le Zodiaque

En tournant autour du Soleil chaque année, la Terre nous présente le ciel sous des aspects différents. La partie que nous voyons chaque nuit est celle qui est au-dessus de l'horizon. Pendant la journée, il y a des étoiles derrière le Soleil, que celui-ci nous empêche de voir par sa lumière. Nous ne voyons donc, à chaque saison, que celles qui lui sont opposées. Il y a donc des constellations d'hiver, de printemps, d'été ou d'automne.

Au cours de l’année, le Soleil se profile devant chaque constellation zodiacale à son tour. La constellation en question, masquée par la lumière du Soleil, demeure invisible pendant quelques temps. Jusqu’à ce que, la Terre s’étant déplacée, le Soleil ne soit plus devant la constellation.

Les constellations zodiacales ont été définies par les Babyloniens. Peuple pastoral, ils ont associé les figures dans le ciel à des périodes de l’année en relation avec l’agriculture et l’élevage. Le ciel leur servait ainsi de calendrier. Une petite explication est nécessaire pour comprendre le sens des signes du zodiaque. Les constellations zodiacales entourent notre système solaire par un grand cercle sur la sphère céleste. Les Poissons et la Vierge, par exemple, sont à l’opposé l’une de l’autre.

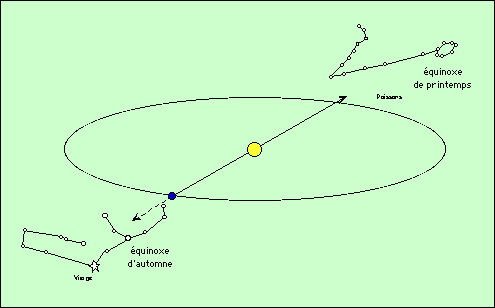
Au moment de l’équinoxe de printemps, la Terre se trouve dans la position indiquée sur la figure ci-dessous : le Soleil se profile devant les Poissons. Lorsqu’il est midi, c’est donc cette constellation qui culmine dans le ciel (bien qu’on ne puisse la voir). Si vous regardez le ciel à minuit, vous découvrirez donc au méridien la constellation exactement opposée. Si vous connaissez l’ordre de succession des constellations, il est donc facile de savoir dans laquelle se trouve le Soleil : vous regardez quelle constellation culmine à minuit ; le Soleil est dans celle qui lui est opposée !

Deux constellations sont opposées si l’une se couche lorsque l’autre se lève… L’ordre est le suivant :

Les dates supérieures correspondent au passage du Soleil au méridien autour de midi. Donc lorsque la constellation est invisible. Les dates de la partie inférieure sont décalées de six mois, et indiquent le passage de la constellation au méridien vers minuit, donc lorsqu’elle est le plus facilement observable. Vous voyez par exemple que le Sagittaire est au méridien aux alentours de minuit en juin-juillet.

Les Babyloniens ont nommé les constellations zodiacales en fonction de leurs activités de bergers et de paysans. Ainsi, au début du printemps, lorsque naissaient les agneaux, ils ont nommé Bélier la constellation dans laquelle se trouvait le Soleil. Au moment des labours, pour lesquels ils utilisaient des bœufs tirant la charrue, la constellation contenant le Soleil a pris le nom de Taureau. Le Cancer est plus difficile à définir. Si on regarde le soleil couchant tous les soirs au cours d’une année, on le voit se déplacer de soir en soir, du sud vers le nord pendant l’hiver et le printemps, puis du nord vers le sud en été et automne. Lorsque le Soleil change sa marche, autrement dit marche a reculons, il fait penser à une écrevisse. D’où le nom de la constellation associé, Écrevisse ou Cancer (crabe).

Je crois entendre votre objection : la constellation qui contient le Soleil sur la figure est celle des Poissons, et non le Bélier comme il est dit dans le texte ! Ce n’est pas une erreur, mais la conséquence d’un phénomène astronomique important, nommé précession des équinoxes. Au moment où les Babyloniens ont nommé les constellations, le Soleil se trouvait effectivement dans le Bélier au début du printemps. Mais le plan de l’équateur terrestre tourne lentement, et l’équinoxe de printemps est maintenant dans les Poissons. Il n’y restera d’ailleurs plus très longtemps, car il va passer dans le Verseau (le sens de la précession des équinoxes est de droite à gauche dans le tableau ci-dessus).

D’une façon analogue, les 12 constellations antiques du zodiaque ont été définies.

Si vous trouvez, dans une documentation, les coordonnées d’un astre, mais pas l’indication de la constellation dans laquelle il se trouve, la petite Applet ci-dessous vous aidera (elle n’utilise pas les limites exactes, très complexes, des constellations, et donne donc plusieurs constallations candidates) :

applet permettant de déterminer la constellation correspondant à des coordonnées équatoriales données.
Vous trouvez les constellations susceptibles d’abriter l’objet. Recherchez-le ensuite sur une carte.

Dans l’hémisphère sud, il y a beaucoup plus d’océans que de terres émergées. Et les peuples habitant ces régions ne nous ont pas laissé de noms pour les constellations (on n’a peut-être pas trop cherché d’ailleurs). Toujours est-il que ce sont les marins du nord qui, en découvrant ces régions, ont défini et nommé les constellations. On y trouve des choses curieuses : le Microscope, la Machine Pneumatique, le Sextant, la Boussole, la Mouche, l’Oiseau de Paradis, le Toucan… Une grande constellation a été définie, qui a pris le nom de Navire (Argos ; Argo était le bateau des Argonautes, compagnons de Jason à la recherche de la toison d’or)). Bien trop grande, cette constellation a été divisée, et chaque morceau a pris le nom d’une partie du navire. C’est ainsi qu’on trouve les Voiles et la Carène.

La définition usuelle des constellations, dont les frontières étaient floues, était insuffisante pour les besoins des astronomes. Ils ont voulu conserver leurs noms, mais en fixer les limites. C’est ce qu’a fait l’Union Astronomique Internationale (UAI). La carte ci-dessous montre bien la complexité des limites d’une constellation. Ces limites sont parallèles aux axes de coordonnées, et s’adaptent le mieux possible aux contours anciens, arrondis et mal définis.

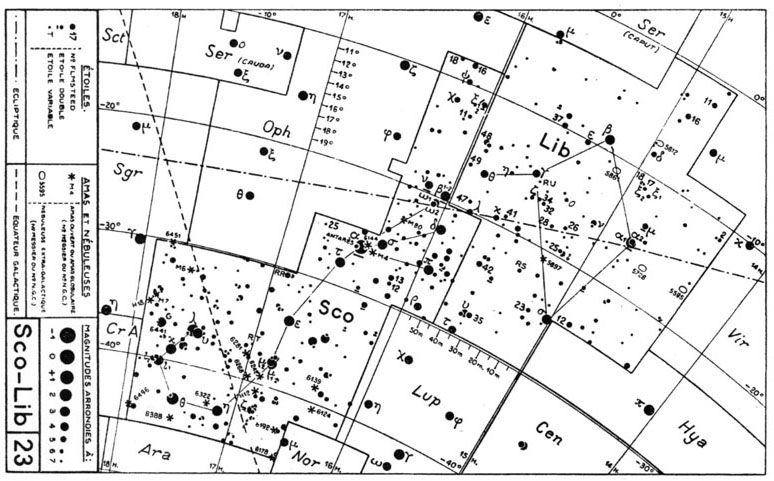
carte du Scorpion et de la Balance, Société Astronomique de France

L’écliptique est la ligne en double pointillés. Le zodiaque s’étend de 5° de part et d’autre. On remarque sur cette carte que le Scorpion est tout juste dans le zodiaque : seule la tête en fait partie. Et une autre constellation, Ophiucus, le Serpentaire en français, se trouve entre le Sagittaire et le Scorpion. De ce fait, le zodiaque comprend maintenant treize constellations et non douze ! (ceci a-t-il une importance ?)

2.3 Noms des étoiles

Les étoiles les plus brillantes et les plus remarquables ont été nommées par les bergers de Mésopotamie. Ensuite, les Grecs, les Egyptiens, les Arabes ont contribué à cette première reconnaissance du ciel.

Voici quelques noms avec une explication :

Lorsque certaines personnes ont tenté de faire œuvre scientifique en étudiant le ciel, il leur est vite apparu la nécessité de nommer un plus grand nombre d’étoiles. Bayer, en 1603 dans l’Uranometria, a choisi de nommer les étoiles avec des lettres grecques, et le nom de la constellation. La plus brillante est appellée α, la seconde plus brillante est β, etc. Les étoiles qui possédaient des noms, les plus brillantes, ont hérité en plus de cette dénomination. Par exemple, α du Lion (Régulus) ou bien β du Cygne (Albireo). De même, les astronomes ont traduit les noms des constellations en latin, langue morte et donc universelle. Le latin présente des déclinaisons. De ce fait, il faut utiliser le génétif pour nommer les étoiles : on dira α Andromedæ et non pas α Andromede. Pour connaitre tous les noms des constellations et leurs génétifs, vous pourrez consulter le tableau en annexe. Ce tableau présente en plus les abbréviations en trois lettres des noms des constellations, qui ont été également standardisées par l’UAI. L’étoile ci-dessus est alors notée α And, et ceci se lit α Andromedæ.

Ceci permet de nommer un plus grand nombre d’étoiles, mais l’alphabet grec est limité.

Aux alentours de 1700, John Flamsteed a dessiné d’excellentes cartes du ciel, et a classé les étoiles d’ouest en est dans chaque constellation. Joseph Lalande les a ensuite numérotées dans cet ordre. Bien sûr, cette classification s’adresse seulement aux étoiles visibles à l’œil nu. On utilise le numéro de Flamsteed pour les étoiles qui n’ont pas de lettre grecque.

D’autre part, il est très difficile de repérer une petite étoile faible parmi toutes les autres… Seule son adresse dans le ciel permet de la retrouver ! L’adresse d’une étoile, ce sont ses coordonnées, mesurées précisément. Alors, les astronomes ont constitué des catalogues contenant des centaines de milliers d’étoiles, avec leurs positions et leurs caractéristiques. Mais il y a dans notre voisinnage, notre Galaxie, 200 milliards d’étoiles ! Aucun catalogue ne peut les contenir toutes… Il faut donc se limiter, et ceci se fait de deux façons différentes :

•  en ignorant les étoiles faibles, et cataloguant toutes les étoiles du ciel plus brillantes qu’une limite donnée ;
•  en ne considérant que les étoiles ayant des propriétés physiques particulières bien définies, et ignorant toutes les autres, même brillantes.

C’est pour cette raison qu’il existe de nombreux catalogues, chacun ayant été construit dans un but un peu particulier.

Avant de parler des catalogues modernes, il faut dire que les Babyloniens, déjà, avaient constitué des listes rudimentaires d’étoiles. C’était il y a 6.000 ans à peu près. Ensuite, on a connaissance d’un catalogue établi par Hipparque en 127 avant JC, mais il a été détruit. Le premier catalogue ancien dont on dispose est celui de Claude Ptolémée, publié dans l’Almageste en 137 après JC. Il contient 1.028 étoiles. Plus tard, les Arabes au Moyen-Age et Tycho Brahé en 1594 ont constitué des catalogues de même importance. Pour trouver mieux, il faut attendre l’invention de la lunette, et son usage par Galilée.

Les catalogues publiés au XVII^e siècle (Lacaille, Bradley, Lalande) contenaient de 10.000 à 47.000 étoiles. Le catalogue d’Argelander publié en 1862 à Bonn, qui a pris le nom de Bonner Durchmusterung (Catalogue de Bonn), contenait 324.000 étoiles, et il a été complété en 1886 par 134.000 étoiles de l’hémisphère sud. Les étoiles de ce catalogue sont désignées par les initiales du catalogue BD, suivies de leur numéro. En 1914 a été terminé un autre supplément du BD, nommé Cordoba Durchmusterung (Catalogue de Cordoue, initiales CD), et qui contient 570.000 étoiles. Ce travail gigantesque a été fait visuellement… mais avec des télescopes bien sûr, puisque la plupart des étoiles référencées sont invisibles à l’œil nu.

L’apparition de la photographie, permettant d’enregistrer des étoiles plus faibles que celles visibles dans le même instrument, a multiplié encore le volume des catalogues. Il devenait impossible de créer un catalogue de toutes les étoiles, et Kapteyn a proposé de choisir quelques zones d’un degré de côté, et de les cataloguer en détail. Ce sont les Selected Areas. Elles sont réparties uniformément sur la sphère céleste. Enfin, signalons l’Atlas photographique du Palomar, réalisé à l’aide du grand Schmidt de cet observatoire. Il couvre tout le ciel visible de ce site jusqu’à la 21^e magnitude.

L’ensemble de tous les catalogues édités regroupe une quinzaine de millions d’étoiles, ce qui est énorme si on regarde le travail nécessaire, et dérisoire en comparaison du nombre d’étoiles de la Galaxie : 15 millions / 200 milliards, c’est-à-dire 0,0075 % du total…

Un autre catalogue célèbre, qui contient des objets autres que les étoiles, a été réalisé par le français Charles Messier. Ce brave homme était un chercheur de comètes méticuleux (activité importante à son époque). Il observait donc le ciel régulièrement, connaissait par cœur toutes les étoiles visibles avec son instrument, et cherchait tout nouveau point brillant. Les comètes se présentent comme de petites taches floues dans l’oculaire. Or dans le ciel, il y a de telles taches, qui ne sont pas des comètes. Alors, Charles Messier a noté précisément les positions de ces objets, génants pour sa recherche, dans un catalogue qui a pris son nom.

Il se trouve que tous les objets de Messier (ceux de son catalogue) se sont avérés être des nébuleuses de gaz (où naissent des étoiles), ou bien des nébuleuses planétaires (reste d’explosions d’étoiles) ou bien encore des galaxies. Son catalogue a été enrichi, et il est toujours en usage. Les objets sont désignés par la lettre M suivi du numéro. Par exemple, la nébuleuse d’Orion est désignée par M 42.

Sans chercher à être exhaustif, il faut encore signaler le catalogue NGC, ou New General Catalog, établi à la fin du XIX^e siècle par Dreyer. Il désigne en particulier les mêmes objets que le catalogue de Messier, mais il est beaucoup plus riche (et plus récent). Les objets de Messier ont donc tous une désignation dans le NGC, mais on les note souvent par leur nom de Messier. Par exemple, la nébuleuse d’Orion est M 42 ou bien NGC 1976. Le catalogue NGC a été étendu par la suite sous le nom de Index Catalog, dans lequel les objets sont indiqués pas les deux lettres IC (suivies d’un numéro).

Signalons enfin qu’il existe maintenant des catalogues d’objets très faibles ou même invisibles, mais très brillants dans d’autres longueurs d’onde (radio, ultraviolet, infrarouge, gamma, X). Le catalogue 3C (3^e catalogue des radiosources de Cambridge) est un très important catalogue de radiosources. En 1962, il a été étendu : 3CR, 3^e catalogue de Cambridge révisé.

2.4 Magnitude visuelle

Les étoiles ont été classées par éclat décroissant par Claude Ptolémée. Il a appellé grandeur l’impression de brillance d’une étoile : les plus brillantes à l’œil nu sont de la première grandeur, les plus faibles de la sixième. Cette définition élémentaire correspond à la capacité de discrimination de l’œil, elle donne une indication grossière insuffisante pour un usage scientifique. En particulier, toutes les étoiles brillantes sont qualifiées de première grandeur, même si leurs éclats sont très différents. On remarque que le nombre qui exprime la grandeur est d’autant plus élevé que l’étoile est moins brillante.

Plus tard, on a remplacé le mot grandeur, imprécis, par celui de magnitude (du latin magnus, grand). Les magnitudes déterminées comme précédemment sont appelées magnitudes visuelles.

Après l’invention de la lunette, on a prolongé les magnitudes vers le haut (vers les étoiles moins brillantes, invisibles à l’œil nu). Plus performants sont les instruments d’observation, plus faibles sont les étoiles visibles. Et leur nombre augmente très vite avec la magnitude limite accessible :

Une analyse photométrique a montré qu’en passant d’une magnitude à la suivante, l’éclat de l’étoile diminue d’un facteur 2,5. Elle est 2,5 fois moins lumineuse. Donc, si on ajoute 1 à la magnitude, on multiplie la luminosité par 2,5 : ceci prouve que l’échelle des magnitudes est logarithmique, et explique la formule ci-dessous.

Actuellement, on est capable de photographier des étoiles de magnitude supérieure à 30, qui sont 1.000 milliards de fois moins brillantes que les étoiles de première magnitude…

L’éclat apparent d’une étoile dépend de deux choses :

•  sa luminosité, qui caractérise le flot de lumière qu’elle émet. Une ampoule de 100 W émet plus de lumière qu’une ampoule de 60 W ;
•  sa distance à la Terre. Une ampoule de 100 W, vue à 100 mètres, semble moins brillante qu’à 10 mètres.

2.5 Magnitude absolue

On définit maintenant la magnitude absolue, comme étant la magnitude qu’aurait l’étoile si elle était à la distance standard de 10 parsecs (32,6 A.L., soit 32,6 10¹³ km). Si la magnitude absolue d’une étoile est plus petite que celle d’une autre, elle est réellement plus brillante, elle émet davantage de lumière (si vous mettez des ampoules de 60 W et 100 W à 100 mètres de vous, les plus fortes paraîtront plus brillantes).

Si d est la distance de l’étoile en parsecs, M sa magnitude absolue et m sa magnitude visuelle, alors :

La calculette ci-dessous vous permet de calculer l’une des trois variables en fonction des deux autres. Elle vous donne l’expression de chaque variable permettant son calcul, tirée de la définition ci-dessus.

Si on connait m (la magnitude visuelle mesurée) et d (sa distance mesurée par une méthode trigonométrique), alors on peut calculer sa magnitude absolue. Par ce moyen, on peut déterminer la magnitude absolue des astres proches (suffisamment pour que la parallaxe, c’est-à-dire la distance, puisse être déterminée). Fort heureusement, cette distance est assez grande pour qu’elle englobe tous types d’astres (hormis les quasars).

La parallaxe d’une étoile est l’angle sous lequel on verrait, depuis cette étoile, le rayon de l’orbite terrestre. Elle permet de rattacher la distance des étoiles à ce rayon, qu’on peut mesurer en kilomètres.

2.6 Parallaxe spectroscopique, module de distance

Réciproquement, si on connait la magnitude absolue d’une étoile, et sa magnitude visuelle, on peut en déduire sa distance. Or certaines étoiles sont si particulières, qu’elles ont toutes la même magnitude absolue (variables de type RR Lyræ par exemple). Si on est capable de les reconnaître (par leur spectre…), on connait donc cette dernière. La mesure de leur magnitude apparente permet alors facilement d’évaluer leur distance, grâce à la relation m - M = 5 log d - 5. Cette méthode est nommée parallaxe spectroscopique.

On appelle module de distance la quantité :

Exemple : l’amas M3 contient des variables RR Lyræ dont la magnitude absolue est M = 0,6. On les observe à la magnitude apparente m = 15,8. Utilisez la calculette ci-dessus pour calculer la distance de l’amas.

Réponse : 11 kilo parsecs (11.000 pcs).

De la magnitude absolue, on peut déduire la luminosité L par :

Certaines étoiles, qui étaient classées dans la première magnitude par les Anciens, sont en fait plus brillantes si on effectue une mesure de magnitude à l’aide d’une cellule photoélectrique. On a donc défini aussi des magnitudes négatives. Sirius, par exemple, est de magnitude -1,45.

Pour bien comprendre ce que sont les magnitudes visuelle et absolue, indiquons enfin que le Soleil présente une magnitude visuelle de -26,72. Elle correspond à une magnitude absolue de +4,8. A 10 parsecs, il serait à peine visible à l’œil nu !

Contrairement à la magnitude apparente, qui dépend de la distance, la magnitude absolue est une propriété intrinsèque des étoiles ; elle ne dépend que de leurs propriétés physiques.

Il faut, pour fixer les choses, donner une valeur à la constante. On la choisit telle que les magnitudes absolues du Soleil soient : M_B = 5,48 dans la bande spectrale autour de 0,436 µm (bande B, dans le rouge), et M_V = 4,83 dans la bande autour de 0,545 µm (bande V, dans le vert).

2.7 Magnitude absolue bolométrique

Cette dernière remarque montre que l’on peut définir la magnitude absolue dans un domaine restreint de longueurs d’onde. Ceci permet de comparer les couleurs des étoiles. Mais a contrario, on peut considérer la magnitude absolue correspondant à tout le domaine spectral. On parle alors de magnitude absolue bolométrique. Elle considère l’ensemble de la lumière émise, y compris dans l’infrarouge et l’ultraviolet. Certaines étoiles brillent plus dans l’un de ces domaines que dans le visible.

3 Les positions

3.1 Distance des étoiles

Pour les Anciens, les étoiles étaient toutes à la même distance de nous, collées sur la sphère des fixes. Mais n’oublions pas que la Terre était au centre de cette sphère, il ne pouvait donc pas y avoir de mouvements des étoiles, mise à part leur rotation diurne. Lorsque Copernic a introduit son système héliocentrique, il est devenu évident que la Terre devait se déplacer au cours de l’année autour du Soleil, et que les étoiles devaient présenter un mouvement apparent pour nous. Exactement de la même manière que les arbres du paysage semblent défiler devant nous quand nous déplaçons en train. Or ce mouvement apparent des étoiles est totalement insaisissable à l’œil nu. Les détracteurs du système héliocentrique en ont fait un argument contre cette idée, alors que ses partisans en ont conclu que les étoiles devaient être très loin ! En effet, les objets lointains ne changent guère de position apparente si on se déplace peu. De notre train, la montagne au loin semble immobile.

On sait bien maintenant que Copernic avait raison, et que les étoiles sont très loin. La mesure de leurs distances est un problème très difficile, qui a été résolu il y a peu de temps. Les étoiles nous apparaissent comme des points sur la voûte céleste. De notre point d’observation (la Terre) nous n’avons pas la profondeur. Donc pas les moyens de mesurer des distances sans mettre en œuvre des méthodes spéciales.

La diversité de ces méthodes se justifie par leur domaine d’application : la plus précise se limite au voisinage très proche du Soleil. Plus loin, il faut utiliser une méthode moins directe, moins précise. Et plus on s’éloigne, plus la précision des critères se dégrade. Cependant, il existe plusieurs méthodes pour estimer la distance d’une étoile donnée : en les comparant, on arrive à une valeur assez précise.

Toutefois, toutes les méthodes sont basées sur les propriétés physiques des étoiles, et leur précision dépend de la stabilité de ces propriétés. Il convient donc d’étudier en priorité la structure et l’évolution des étoiles. L’étude des distances fait l’objet d’un chapitre à part.

Pour la mesure des distances stellaires, l’unité que nous avons définie pour les planètes ne convient pas. On a défini deux nouvelles unités, l’année-lumière et le parsec.

L’année-lumière est la distance parcourue par la lumière en une année. Comme la lumière se déplace à 300.000 km par seconde, il suffit de multiplier ce nombre par le nombre de secondes qu’il y a dans l’année. Ce nombre de secondes est : 60 × 60 × 24 × 365 = 31.536.000 secondes. L’année-lumière vaut donc en kilomètres :

31.536.000 × 300.000 = 9.460.800.000.000 km, soit approximativement (on n’en est pas à quelques milliards de kilomètres près) 10.000.000.000.000 km.

On peut lire : 10.000 milliards de km. On retiendra :

1 AL = 10¹³ km.

L’étoile la plus proche est située à 4,2 années-lumière. Notre galaxie mesure 100.000 années-lumière, et les plus lointaines galaxies connues sont à une dizaine de milliards d’années-lumière…

L’année-lumière pose un problème qui est important en physique : elle définit une nouvelle unité qui n’a aucun rapport avec les précédentes. Puisqu’une année-lumière vaut 9.460.800.000.000 km, et l’unité astronomique 149.597.870,66 km, on en déduit facilement que 1 AL = 63.242 UA. On dit que ces deux unités sont rattachées l’une à l’autre, mais elles sont de nature différente.

3.2 Mouvements propres

Les mouvements que nous avons évoqués à propos de la mesure des distances étaient des mouvements apparents, produits par la rotation de la Terre autour du Soleil. Ceux que nous allons voir maintenant sont des déplacements des étoiles elles-mêmes, les unes par rapport aux autres. Pour différencier ces deux types de mouvements, il y a un critère simple : les mouvements apparents dus à la rotation de la Terre autour du Soleil sont périodiques, de périodes 1 an. Les mouvements propres des étoiles sont non périodiques, ils vont toujours dans le même sens (à cause du principe d’inertie).

Les étoiles se déplacent donc, mais tellement lentement en projection sur la sphère céleste qu’il faut des mesures très précises pour détecter leurs mouvements. Ou alors…

Les mouvements propres des étoiles ont été découverts par Sir Edmund Halley, celui de la comète. Il a comparé les positions de certaines étoiles brillantes mesurées en 1718, à celles faites dans l’Antiquité. Le temps séparant les deux séries de mesures est assez long pour que le déplacement soit très supérieur aux erreurs de mesure. Il a ainsi mis fin au dogme de la sphère des fixes. Il a notamment déterminé les mouvements propres d’Arcturus et d’Aldébaran. Sa méthode utilisait donc des mesures de précision médiocre (de l’ordre de la minute dans l’Antiquité), mais un temps très long pour que le déplacement soit très important.

Maintenant, les moyens d’observation permettent de déterminer les mouvements propres de nombreuses étoiles, notamment grâce à la précision des données du satellite Hipparcos, de l’Agence Spatiale Européenne.

L’étoile possédant le mouvement propre le plus important est l’étoile de Barnard ; elle se déplace sur le ciel de 10,3″ par an. C’est une petite étoile de magnitude 10. L’étoile de Kapteyn se déplace de 8,8″ par an. On voit que ces valeurs sont très faibles, c’est pourquoi les étoiles semblent fixes en première approximation.

Ces étoiles sont toutes proches, car sinon la distance interdit de mesurer les mouvements propres dans un temps raisonnable. Pour les étoiles dont le mouvement propre et la distance sont connus, il est possible de déterminer la vitesse linéaire en projection sur la sphère céleste (en km/s).

Nous avons vu que les constellations ne sont que des apparences dues à la perspective. Puisque les mouvements propres des étoiles changent leurs positions respectives au cours du temps, les constellations doivent se déformer. C’est le cas par exemple de la Grande Ourse, qui était très différente il y a 100.000 ans, et qui sera encore autre dans 100.000 ans. L’animation ci-dessous vous montre son évolution passée et future.

Votre navigateur ne supporte pas canvas...

	Tracer	Trajet	Nommer

Il est facile de voir que Benetnash, il y a 100.000 ans, nous aurait paru appartenir à un autre astérisme car elle était éloignée des autres étoiles qui constituent la Grande Ourse actuelle. De même, dans le futur, Benetnash, Mizar, Alioth, Mégrez et Phegda formeront un astérisme bien évident. Dubhé et Mérak, trop éloignées, pourraient appartenir à une autre constellation, avec d’autres étoiles dont elle se seront rapprochées…

Les constellations ne sont vraiment que des illusions d’optiques dues aux positions de la Terre et des étoiles constituantes. Elles sont aussi irréelles que le dessin fait à un instant donné par les voitures rouges circulant dans une ville.

Qu’en pensent les astrologues ?

3.3 Projection du mouvement sur la sphère céleste

Les mouvements propres des étoiles se font dans n’importe quelle direction, sans rapport avec la direction d’observation depuis la Terre. Les mouvements dont nous venons de parler sont la projection du mouvement réel sur la sphère céleste, on les appelle mouvements tangentiels (parce que c’est la projection du mouvement sur la tangente à la sphère céleste). La projection perpendiculaire se fait selon l’axe de visée ; on l’appelle mouvement propre radial (suivant le rayon de la sphère céleste). Le mouvement propre radial n’entraîne aucun déplacement par rapport aux autres étoiles (une voiture qui vient droit vers vous ne semble pas se déplacer par rapport aux arbres du paysage). Le seul moyen de détecter ce déplacement est la spectroscopie.

Les vitesses mesurées sont comprises entre 20 et 60 km/s pour la grande majorité, mais les plus rapides atteignent jusqu’à 600 km/s.

Nous allons passer maintenant aux propriétés physiques des étoiles.

4 Propriétés physiques

4.1 Masse d’une étoile

Comme pour la distance, la masse d’une étoile est très difficile à mesurer, sauf cas particulier. Son observation ne nous apprend rien à ce sujet. Mais certaines étoiles sont doubles, et tournent l’une autour de l’autre. Dans un tel cas, l’application des lois de la gravitation, ou plus simplement d’une version améliorée des lois de Kepler, nous permet de calculer les masses des composantes.

Toutes les étoiles ne sont pas doubles, et donc beaucoup échappent à cette méthode. Nous n’avons aucun moyen direct de mesurer la masse des étoiles simples. Mais la théorie des étoiles nous apprend que d’après leurs propriétés physiques, on peut les classer en divers types. Et que des étoiles de même type ont la même masse.

Alors, si on trouve quelques étoiles de chaque type faisant partie d’un couple, on pourra en déduire leur masse, et par suite celle des étoiles simples de même type.

Dans le cas particulier du Soleil, la mesure de la masse est très simple, car on dispose de tout son cortège planétaire pour appliquer les lois de Kepler. On trouve 2.000.000.000.000.000.000.000.000.000.000 kg.

Avez-vous réussi à lire ce nombre ? Vous pouvez l’exprimer en tonnes, ça supprimera toujours 3 zéros…

On peut le réécrire sous la forme 2 10³⁰ kg, qui est plus lisible, mais guère plus évocatrice…

Devant la difficulté à manier des nombres pareils, qui n’ont guère de signification pour nous, les astronomes ont mis en usage une unité plus pratique : tout simplement la masse du Soleil ! La masse d’une étoile sera donc donnée en masses solaires, ce qui est noté M. Une étoile de 2 M est donc deux fois plus massive que notre Soleil. Ainsi, les masses sont directement comparables.

On a observé des étoiles de masses très diverses, comprises entre 0,08 M et 120 M.

Nous verrons que la masse est le paramètre le plus important d’une étoile ; c’est lui qui détermine en particulier sa durée de vie et son évolution.

On retiendra :

1 M = 2 10³⁰ kg

La masse d’une étoile n’est pas quelconque. On peut considérer qu’elle est comprise entre les valeurs suivantes :

0,08 M < M_* < 120 M

•  la limite inférieure correspond à une température centrale (≃7 millions de degrés) juste suffisante pour permettre la fusion de l’hydrogène. Elle est définie par les propriétés physiques de l’hydrogène, et par la gravitation. Au-dessous de cette limite, la fusion du deutérium (hydrogène lourd) est possible. Mais cet isotope est rare, et la production d’énergie restera très faible. Les étoiles dont la masse est comprise entre 0,01 et 0,08 M sont des naines brunes : on qualifie ainsi des étoiles qui possèdent une source d’énergie propre par le deutérium, mais qui sont incapables de fusionner l’hydrogène. Au dessous de 0,01 M, ce sont des planètes (aucune production d’énergie nucléaire).
•  la limite supérieure est beaucoup moins bien définie, car elle dépend de nombreux paramètres. En fait, rien n’interdit la formation d’étoiles plus massives que 120 M, mais le débordement d’énergie nécessaire pour éviter leur écrasement gravitationnel est tel, qu’elles sont instables  : les couches extérieures sont violemment expulsées. Un bel exemple nous est donné par η Carinæ, qui atteint 150 M.

Un moyen pratique de se rappeler l’intervalle de masse des naines brunes : en anglais, elles sont comprises entre seventeen (17) et seventy (70) masses joviennes (masses de Jupiter).

4.2 Luminosité

La luminosité d’une étoile représente la quantité d’énergie qu’elle émet dans l’espace à chaque seconde. Elle concerne toutes les longueurs d’onde, de l’infrarouge jusqu’à l’ultraviolet. Or seul le visible est… visible ! Donc, la luminosité mesurée simplement d’après les observations télescopiques ne concerne que ce domaine. Si on mesure réellement toutes les longueurs d’onde, on utilise la magnitude absolue bolométrique, et on l’utilise pour déterminer la luminosité exacte de l’étoile.

La luminosité varie dans de très grandes proportions. Pour s’en rendre compte, il faut mesurer la brillance apparente des étoiles, et mesurer leur distance. On en déduit la quantité de lumière qu’elles émettent, donc leur luminosité. La mesure de la distance est difficile, et n’est très précise que pour les étoiles assez proches. Depuis la Terre, elle est fortement limitée par l’atmosphère et les mesures sont médiocres.

Le satellite européen Hipparcos (ESA) a fait faire à la mesure des distances un bond d’un facteur 10 (mesure des positions 50 fois plus précise que sur Terre, magnitude limite 12,4, 118.000 étoiles mesurées). Et parmi toutes les étoiles dont on connait bien la distance, on rencontre tous les types spectraux. On peut en déduire des lois.

Gaia, satellite également européen (ESA), atteint la magnitude limite 20,7. Il a observé plus d’un milliard d’objets (étoiles surtout), précision de 5 à 600 micro-seconde d’arc (jusqu’à 100 fois mieux qu’Hipparcos). Ces deux instruments ont fait faire à l’astronomie des progrès énormes. Dédiés à la mesure des positions des étoiles, avec leur précision, ils permettent de déterminer les distances précisément. De plus, Gaia fourni des mesures photométriques (brillance des étoiles). De ces informations, on peut déduire les caractéristiques physiques des étoiles, et améliorer considérablement les modèles théoriques.

0,005 L < L_* < 900.000 L

Les étoiles les moins lumineuses sont 200 fois moins brillantes que notre Soleil, et à l’opposé les plus brillantes rayonnent 900.000 fois plus que lui !

4.3 Rayon

Les tailles des étoiles sont aussi fort diverses :

0,02 R < R_* < 1.100 R

Le rayon du Soleil est de 700.000 km. La plus petite étoile a donc un rayon de 0,02 × 700.000 = 14.000 km (c’est seulement le double du rayon de la Terre, la moitié du rayon d’Uranus !). Par contre, la plus grosse a un rayon de 770 millions de kilomètres. C’est la distance de Jupiter au Soleil, ce qui signifie que si cette étoile était à la place de notre Soleil, Mercure, Vénus, la Terre, Mars et Jupiter seraient à l’intérieur…

Le système solaire avec une étoile géante

Ce schéma montre une étoile de taille maximum (en jaune), le Soleil (le petit point rouge au centre, très grossi…), avec les orbites des planètes Mercure, Vénus, la Terre, Mars et Jupiter.

Les premières estimations de la taille des étoiles ont été faites d’après des mesures de luminosité, et de température superficielle. A température égale, les plus lumineuses sont les plus grosses. De cette constatation sont venues les appellations d’étoiles géantes, et de naines. Il n’y a rien d’étonant, en voyant ce schéma, de penser que le Soleil est une naine…

5 Relations importantes

On a trouvé empiriquement des relations entre la masse d’une étoile (de la Séquence Principale) et son rayon ou bien sa luminosité. Attention, ces relations n’indiquent pas comment se comporte une étoile particulière, mais comment varient les propriétés des étoiles lorsqu’on considère des masses croissantes.

Ces relations ont été retrouvées par la théorie, et donnent une idée des propriétés d’une étoile particulière. Il est évident que si l’on veut une plus grande précision, on doit effectuer un calcul direct. Or les équations qui représentent la structure stellaire sont des équations aux dérivées partielles couplées, qui n’admettent pas de solution analytique générale. Pour un cas particulier donné, il faut faire une intégration numérique adaptée.

5.1 Relation masse-rayon

Les lois de puissance sont des formes particulières simples qui permettent d’estimer l’évolution d’une grandeur en fonction d’une autre. Une loi de puissance est de la forme générale

y = x^k

Cette loi donne la valeur de y en fonction de celle de x. Si k > 1, y croît plus vite que x. Si 0 < k < 1 y croît moins vite que x. Si k = 0, y est constante, et vaut toujours 1. Enfin, si k < 0, y décroît lorsque x croît; x^-k = 1 / x^k (si k est positif, -k est négatif). Bien sûr, plus k est grand, plus la variation de y sera rapide.

L’intérêt de ces lois de puissance est la possibilité d’effectuer les calculs analytiques jusqu’au bout. On s’en sert souvent dans la théorie des étoiles. Un cas particulier très important est les modèles polytropiques : on nomme ainsi les modèles dans lesquels la pression interne est une loi de puissance de la masse volumique. Ce cas particulier est totalement intégrable, et donne une solution analytique de la structure stellaire. Malheureusement, les étoiles réelles ne sont pas polytropiques… sauf quelques cas particuliers ! Les naines blanches en font partie, et on connait donc leur structure.

Pour les naines (étoiles sur la Séquence Principale, comme par exemple le Soleil), il existe deux relations masse-rayon, selon la masse de l’objet, différant de la valeur de l’exposant :

La masse étant donnée en masses solaires, le rayon est obtenu en rayons solaires. Si donc M = 1 M , on obtient R = 1 R. Pour M = 2 M (seconde formule), R = 1,74 R ; pour M = 3 M, R = 2,41 R ; pour M = 0,5 M (première formule), R = 0,67 R.

La limite entre les deux relations possède un sens physique : les étoiles de masse inférieure à 1,1 masses solaires ont un intérieur radiatif et une enveloppe convective, c’est le contraire pour les autres. Cette limite sépare la Séquence Principale en Séquence Principale inférieure, et Séquence Principale supérieure.

5.2 Relation masse-luminosité

On observe, et on justifie théoriquement, une relation de même type entre la masse et la luminosité d’une étoile de la Séquence Principale.

On remarque qu’il existe en fait deux relations, avec un exposant un peu différent. Le passage de l’une à l’autre se fait pour les étoiles dont la masse est la même que celle du Soleil. Nous verrons plus loin, en étudiant la source d’énergie des étoiles, que ce passage correspond à la transition entre deux mécanismes différents de fusion de l’hydrogène. Leur rendement étant légèrement différent, la relation qui en dépend doit être différente.

Pour 2 M, la luminosité est 14,7 L. Une étoile deux fopis plus massive que le Soleil émet 15 fois plus d’énergie que lui ; pourtant, elle ne possède que 8 fois plus de matière (hydrogène). Elle a donc plus de "carburant", mais elle le consomme beaucoup plus vite, et sa durée de vie est donc inférieure.

6 Classification

6.1 Types spectraux

Quand on regarde attentivement le ciel, on arrive à distinguer quelques étoiles colorées. C’est le cas par exemple, en hiver, des deux magnifiques étoiles d’Orion : Bételgeuse et Rigel. On voit bien que Bételgeuse est rouge, et Rigel bleue. Cette différence d’apparence traduit une différence de propriétés physiques.

Si vous placez un morceau de fer dans une forge, il va commencer à briller lorsque sa température atteint les 800°. Il est alors rouge sombre. Si on continue le chauffage, il va passer au rouge vif, puis au blanc si on insiste. D’où l’expression chauffé à blanc. Par analogie, on en déduit que la couleur d’une étoile va nous renseigner sur sa température.

Mais la couleur est difficile à apprécier, et ce ne sera pas un bon critère direct de classement. En fonction de la température, les divers éléments chimiques émettent de la lumière, et celle-ci ne dépend pas de leur nature (hydrogène, hélium, ou autre). Elle ne dépend que de la température, et donne un spectre continu coloré du violet au rouge. Par contre, l’atmosphère des étoiles est peu dense, produit très peu de lumière elle-même, et au contraire absorbe une partie de celle produite par la photosphère. L’absorption ne concerne que quelques couleurs très spécifiques, correspondant à des niveaux d’énergie des atomes. Et chaque type d’atome présente un spectre de raies bien précis, et différent de tous les autres. Tout ceci est expliqué dans un chapitre sur les propriétés de la lumière.

On analyse donc la lumière de l’étoile à travers un prisme (ou à travers un réseau de diffraction plus souvent). Selon les raies d’absorption observées, on sépare les étoiles en un certain nombre de classes définies ci-dessous :

Les étoiles O par exemple montrent dans leur spectre des raies d’absorption de l’hélium ionisé (He II) et de l’hélium neutre (He I). Les étoiles B présentent des raies du carbone, mais plus de l’hélium. C’est dû au fait que l’hélium s’ionise à une très haute température, atteinte dans les étoiles O, mais pas dans les B. On remarquera qu’à partir de la classe K apparaissent des raies de molécules. Or les molécules sont fragiles, facilement détruites par la chaleur. Leur présence montre que ces étoiles sont beaucoup moins chaudes.

Les étoiles R et N sont les étoiles carbonées. Ce sont toutes des géantes. Les S sont à faible teneur en carbone.

Remarquez que la température n’est pas un critère de distinction entre les classes spectrales : les étoiles de classes M, S et N ont les mêmes intervalles de températures, mais des compositions différentes.

A l’intérieur de chaque classe, les étoiles sont numérotées de 0 à 9. La valeur 0 correspond aux étoiles les plus chaudes, et 9 aux moins chaudes. Ainsi, le type spectral G par exemple est divisée en G0, G1, … G9, les étoiles G0 ayant une température d’à peu près 6.000 K alors que les G9 n’ont que 4.900 K.

Exemple : La température du Soleil étant d’à peu près 5.700 K, et ses principales raies spectrales étant celles du Calcium ionisé et des métaux, quelle est sa classe ?

Tout d’abord, le tableau ci-dessus montre que les étoiles ayant ces raies principalement sont de type spectral G. Il reste à déterminer la sous-classe.

La classe G va de 4.900 à 6.000 K. Elle s’étend donc sur un intervalle de 6.000 - 4.900 = 1.100 K.

Réparti sur dix sous-classes, cela donne 110 K par classe ; les sous-classes se répartissent donc ainsi :

Il suffit de lire ce tableau pour voir que le Soleil est de classe G2.

Pour être complet sur ce sujet, il faut considérer un ensemble de lettres qui viennent parfois modifier le type spectral, pour rendre compte de certaines particularités. On distingue des préfixes et des suffixes :

Exemple : Proxima Centauri est de type dM5e

Remarque si la Terre orbitait autour d’une naine rouge, pour avoir autant de lumière qu’autour du soleil, elle devrait être 1.000 fois plus près, donc à 150.000 km de l’étoile, soit 2 fois plus près que la Lune…
Si au contraire nous étions autour d’une étoile O, nous devrions être 200 fois plus loin, soit 5 fois plus loin que Pluton…

6.2 Classes de luminosité

La seconde propriété physique importante pour caractériser une étoile est basée sur la quantité de lumière qu’elle émet. A l’œil nu, on voit des étoiles d’éclat variable, mais cette apparence fait intervenir la distance. La magnitude absolue caractérise l’éclat des étoiles, elle est donc une mesure de la quantité de lumière émise.

Cette quantité dépend de deux paramètres :

•  la quantité de lumière émise par unité de surface ;
•  la surface émettrice.

Prenons deux morceaux de fer, l’un ayant une surface double de l’autre. A la même température, le premier émet deux fois plus de lumière.

Les étoiles se comportent de la même façon. A une même température, celle qui émet deux fois plus de lumière a une surface double. Cette remarque a permis de définir les classes de luminosité :

Les noms des classes appellent une explication. Lorsqu’on a compris qu’une grande luminosité correspond à une grande surface, donc un grand diamètre, on a réalisé qu’il existait des étoiles beaucoup plus grosses que notre Soleil, et on les a baptisées Géantes. On en a trouvé de plus grosses encore, dites supergéantes. On a alors réalisé que notre Soleil était finalement une toute petite étoile, donc une naine…

Et au bout du compte, il n’y a pas d’étoiles normales ! ! (tout au moins pour la taille).

La classe V, celle des naines, est qualifiée aussi de Séquence Principale. Ce terme vient du diagramme de Hertzprung-Russel, que nous étudierons plus loin.

Le Soleil étant une naine de la Séquence Principale, est de classe V. Sa dénomination complète est donc G2 V.

6.3 Naines et géantes

Comment a-t-on découvert l’existence d’étoiles naines et géantes, i.e. comment a-t-on pu avoir une idée de leur diamètre, alors que celui-ci était (est encore dans la plupart des cas) totalement inobservable directement ?

Très simplement parce qu’on a observé des étoiles de même température superficielle qui ont des éclats très différents. Une même température de surface implique une même quantité de lumière émise, pour chaque m². Alors, celle qui brille le plus a davantage de m² !

Explicitons :

•  la température de surface est connue par l’analyse de la lumière : on détermine dans le spectre la longueur d’onde où se trouve l’intensité lumineuse maximum, et par la loi de Stéfan-Boltzman, on en déduit la température (c’est ainsi qu’on a mesuré la température de surface du Soleil). On en déduit la quantité de lumière émise par m².
•  on peut mesurer la magnitude visuelle de l’étoile, qui indique son éclat apparent, fonction de sa distance. Pour savoir quelle est la brillance réelle de l’étoile, il faut faire abstraction de sa distance, qui affaiblit son éclat.
•  si l’étoile est assez proche, on peut mesurer sa parallaxe, qui nous donnera sa distance.
•  la magnitude visuelle et la distance nous donnent la magnitude absolue, qui mesure l’éclat intrinsèque de l’étoile. Nous connaissons maintenant la quantité de lumière émise par m² (point 1) et la quantité totale de lumière émise (point 3) ; il suffit de faire une division pour obtenir la surface de l’étoile.

On a ainsi montré que certaines étoiles, de haute température superficielle, émettaient peu de lumière ; donc leur surface était faible : ce sont les naines blanches. On a montré par ailleurs que d’autres étaient assez froides (2.000° de température superficielle) et pourtant très lumineuses : ce sont les géantes rouges.

Plus tard, on a obtenu pour quelques étoiles des mesures plus directes de leur diamètre, qui ont confirmé cette explication.

6 Fonctionnement des étoiles

6.1 Durée de vie sur la Séquence Principale

Eddington a montré que, pour maintenir son équilibre, une étoile doit rayonner une quantité d’énergie proportionnelle à M^3,5.

Nous allons en déduire l’ordre de grandeur de la durée de vie de l’étoile :

La durée de vie de l’étoile est :

•  d’autant plus grande que sa réserve d’énergie est plus grande,
•  et d’autant plus petite que la production d’énergie est plus rapide.

On en déduit qu’elle est proportionnelle à la réserve d’énergie, et inversement proportionnelle au taux de production d’énergie :

durée de vie = réserve d’énergie / taux de production

La réserve d’énergie est proportionnelle à la masse M de l’étoile (plus il y a d’hydrogène, plus elle peut en brûler ; elle brûlera seulement ce qui se trouve dans le cœur, mais c’est une proportion relativement constante) ; on peut donc remplacer ce terme par M. Quand au taux de production de l’énergie, nous avons vu qu’il est proportionnel à M^3,5. Notons V la durée de vie. Elle est donc proportionnelle à :

durée de vie = V ∝ M / M^3,5 = 1 / M^2,5

Le symbole mathématique ∝ signifie : proportionnel à. Il indique que V est égal à 1 / M^2,5 multiplié par une constante : V = k / M^2,5. Il reste à déterminer cette constante.

On exprimera la masse en masses solaires M. La formule doit donner, en particulier, la bonne durée de vie pour le Soleil. Donc si M = 1 M, V = 10, en milliards d’années. Donc 10 = k / 1^2,5 = k. On substitue cette valeur k = 10 dans la formule, et on obtient :

V = 10 / M^2,5 milliards d’années

Calculons la durée de vie de quelques étoiles :

On peut maintenant faire un calcul inverse : fixons une durée de vie, et calculons la masse de l’étoile :

        V = 10 / M^2,5 ⇒ V × M^2,5 = 10 ⇒ M^2,5 = 10 / V ⇒ M = (10 / V)^{1 / 2,5} = (10 / V) ^0,4

Prenant V = 13,7 milliards d’années, on trouve M = 0,88 M.

13,7 milliards d’années représente l’âge de l’Univers. Toutes les étoiles de masse inférieure à 0,88 M, qui se sont formées juste après le Big Bang, ont une durée de vie supérieure à l’âge de l’Univers, et n’ont donc pas fini leur vie (sur la Séquence Principale). Seule la théorie peut donc nous renseigner sur leur avenir.

Enfin, voici une animation qui vous permettra de voir la forme de la courbe. Les valeurs de la masse ont été limitées à l’intervalle de 0,2 à 5 masses solaires, car vous constaterez que la courbe tombe très très vite, lorsque la masse augmente un peu : elle est très creuse. Avec un intervalle plus grand, le creux serait encore plus marqué, et la courbe illisible.

Déplacez le curseur pour considérer des étoiles de diverses masses. Dans la partie haute, vous verrez les valeurs de la masse et de la durée de vie correspondante. Observez les variations très rapides pour les petites masses.

6.2 Température superficielle

On la note en général T_eff (pour température effective).

2.000 K < T_eff < 150.000 K

La température effective du Soleil est de 5.770 K. On voit donc qu’il est parmi les étoiles les plus froides. Heureusement pour nous !

Les étoiles dont la surface est la plus chaude sont des étoiles massives, dont les réactions nucléaires sont très rapides et violentes pour maintenir l’équilibre.

La température superficielle d’une étoile naine s’exprime par :

T_eff = (L / 4 π σ R²)^1/4

σ est la constante de Stefan-Boltzmann.

Certaines étoiles particulières ont aussi une surface très chaude, mais pour une raison un peu différente. Ce sont les étoiles dites de Wolf-Rayet, qui ont perdu leur enveloppe. Ce que nous voyons est donc leur cœur mis à nu, et par conséquent très chaud à cause des réactions nucléaires qui s’y produisent. Par opposition à ces étoiles de Wolf-Rayet, on peut dire que les étoiles normales sont constituées d’un cœur protégé par une couverture.

6.3 Animation

On peut réunir l’ensemble de ces valeurs dans une animation, qui permet de calculer les paramètres d’une étoile naine en fonction de sa masse :

L’axe horizontal (abscisses) représente la masse M de l’étoile, en masses solaires. Les deux courbes montrent l’évolution du rayon R (en jaune) et de la luminosité L (en vert). En haut, le bandeau résume les paramètres de l’étoile : masse, rayon, luminosité, température, durée de vie sur la Séquence Principale (SP), et type spectral. Les trois premiers sont en unités solaires (masses solaires, rayons solaires, luminosités solaires) ; la température est en Kelvins ; la durée de vie en millions d’années.

Vous remarquerez que la courbe rayon présente un point anguleux au niveau de 1,1 masses solaires. Cette particularité vient du changement d’exposant dans la formule : R = M^0,57 avant 1,1 masses solaires, et R = M^0,80 après.

En déplaçant le curseur rouge, on fait varier la masse de l’étoile, et tous ses paramètres. On peut ainsi afficher les caractéristiques de l’étoile choisie. Il est remarquable de constater que les types spectraux ne sont pas équivalents dans ce graphique : le type B s’étend depuis M = 2,55 M jusqu’à 15,9 alors que le type K ne couvre que l’intervalle de masses de 0,4 à 0,72. Leur importance sur le graphique est très différente, et les types représentant les faibles masses sont mal représentés.

Le bouton zoom en bas permet de remédier à ce défaut, en retraçant le graphique pour les étoiles en-dessous de 2 masses solaires. Vous y retrouverez la petite discontinuité due au changement de fonction sur la courbe des rayons. Cette limite défini la Séquence Principale inférieure (en dessous de 1,1 masses solaires), et supérieure.

6.4 Vitesse de rotation

Toutes les étoiles tournent sur elles-même, mais il faut une analyse assez fine pour le mettre en évidence. L’observation directe le montre pour le Soleil, grâce à sa grande proximité. Mais on ne peut résoudre la surface d’aucune autre étoile pour y voir des taches animées d’un mouvement de rotation. La mesure d’une vitesse de rotation ne peut donc se faire que par une méthode indirecte.

Prenons le cas d’une étoile dont l’axe de rotation soit perpendiculaire à la ligne de visée (la Terre se trouve dans son plan équatorial). Elle nous présente un disque dont la partie droite (par exemple) se rapproche de nous par la rotation, alors que la partie gauche s’éloigne. La lumière émise par la matière qui se trouve à droite et qui s’approche de nous, est donc décalée vers le bleu par effet Doppler. Par contre, la matière du côté gauche s’éloigne, et la lumière qu’elle émet est décalée vers le rouge.

L’animation ci-dessous le montre :

Votre navigateur ne supporte pas canvas...

	Inclinaison

On voit une étoile présentant quelques taches, qui visualisent la rotation. Le spectre de cette étoile apparaît, et montre quatre raies de l’hydrogène. La vitesse de rotation est initialement très faible, et les raies sont fines. Si on fait varier la vitesse de rotation de l’étoile, on voit les raies s’élargir accélération) ou se rétrécir (ralentissement).

Supposons l’étoile fixe par rapport à la Terre (si ce n’est pas le cas, l’ensemble du spectre sera décalé d’une même valeur).

Considérons la lumière émise par le centre de l’étoile. Elle nous parvient sans décalage (on la suppose fixe par rapport à la Terre). Les raies d’absorption produites par la chromosphère seront donc à leur position normale dans le spectre.

La lumière qui nous parvient du bord droit, qui se rapproche, est décalée vers le bleu. Par conséquent, nous recevrons moins de lumière dans ce domaine du spectre, qui paraîtra assombrie. Il en est de même à l’autre bord de l’étoile, qui s’éloigne, et produit une raie décalée vers le rouge. Au total, la raie est très sombre au centre, et s’étale sur les ailes en diminuant d’intensité.

Ce mécanisme produit un profil particulier de la raie, dont l’analyse permet de mettre en évidence une rotation, et de la mesurer.

Nous ne sommes cependant pas au bout de nos peines. Si nous inclinons l’axe de rotation, la largeur de la raie diminue ! L’explication est très simple : la vitesse de rotation apparente, par rapport à nous, est plus faible que si l’axe était bien perpendiculaire à la ligne de visée. A la limite, si l’axe pointe exactement vers nous, la rotation apparente est nulle, est les raies ne seront pas élargies. La forme de la raie n’est pas affectée, et rien ne nous permet de mesurer l’angle d’inclinaison.

Dans ces conditions, on peut penser qu’il est vain de tenter cette mesure, puisque nous ne saurons pas si nous mesurons la vitesse réelle (inclinaison nulle) ou seulement sa projection sur la ligne de visée, la vitesse exacte nous restant inaccessible.

C’est compter sans les statistiques ! On peut supposer que les étoiles ayant des propriétés physiques semblables partageront aussi une vitesse de rotation du même ordre. Les astronomes ont donc fait cette mesure pour un grand nombre d’étoiles de même type spectral. Et ils ont montré effectivement que les vitesses observées se confinent dans une certaines fourchette de valeurs. En supposant (ce qui est parfaitement raisonnable) que les orientations des axes de rotation sont distribuées au hasard, ils ont obtenu une vitesse représentative de chaque type spectral.

Pour les étoiles du bas de la Séquence Principale, entre les types M et G, la vitesse de rotation à l’équateur varie de 1 à 5 km/s. Mais on observe une discontinuité, nommée discontinuité rotationnelle, vers le type spectral F. Les vitesses sautent brutalement à 100 km/s ! Elles continuent d’augmenter, et atteignent 200 km/s pour le type spectral B.

Il y a une explication physique, au moins dans les grandes lignes, à cette discontinuité : elle se produit lorsque l’enveloppe convective disparaît. Celle-ci devient de plus en plus fine lorsqu’on monte dans les types spectraux, et devient inexistante pour le type F. Le transport d’énergie est à partir de là totalement radiatif.

Or la couche convective joue un grand rôle dans l’entretien du champ magnétique de l’étoile. Lorsqu’elle disparaît, une modification de ce champ entraîne une variation de la vitesse de rotation.

6.5 Problème de la rotation

Les étoiles se formant par effondrement d’un nuage d’hydrogène en rotation initiale, on peut calculer à quelle vitesse elle devraient tourner. L’image classique d’une patineuse qui tourne sur elle-même, bras écartés, puis ramène les bras le long du corps est très explicite : sa vitesse de rotation augmente beaucoup ! Les physiciens ont formalisé ce phénomène grâce à la notion de moment angulaire (moment n’a ici rien à voir avec le temps).

Considérons une sphère homogène (la masse est régulièrement répartie à l’intérieur). Pour la faire tourner, il faut lui fournir de l’énergie. On mesure la résistance à cet entraînement par le moment angulaire, qui vaut pour une sphère homogène :

I = 2/5 M R²

Si ω est la vitesse angulaire de rotation, le moment angulaire, qui mesure en quelque sorte la quantité de rotation, s’exprime par :

L = I ω = 2/5 M R² ω

Or, dans une transformation sans échange d’énergie avec l’extérieur, le moment angulaire se conserve. Lorsque notre nuage d’hydrogène se contracte pour former une étoile, son moment angulaire aura donc la même valeur avant et après la contraction.

Prenons par exemple, un nuage comptant 10¹⁰ atomes d’hydrogène par cm³, et ayant une masse solaire. Supposons qu’il tourne en 1.000 ans sur lui-même. Il se contracte pour donner une étoile de la taille du Soleil, soit 7 10⁸ m. Quelle sera sa vitesse de rotation après contraction ?

On utilise la conservation du moment angulaire :

L = I₁ ω₁ = I₂ ω₂

où I₁ et ω₁ représentent le moment angulaire et la vitesse angulaire avant contraction, et I₂ et ω₂ les mêmes quantités après contraction. La vitesse angulaire est :

ω = 2 π / P

où P est la période. Donc

ω₁ = 2 π / P₁ et ω₂ = 2 π / P₂.

et L = I₁ ω₁ = I₁ 2 π / P₁ = I₂ ω₂ = I₂ 2 π / P₂

Par suite, en supposant que l’étoile est une sphère homogène  :

I₁ / P₁ = I₂ / P₂

I₁ = 2/5 M R₁² et I₂ = 2/5 M R₂²

d’où :

I₁ / P₁ = 2/5 M R₁² / P₁ = I₂ / P₂ = 2/5 M R₂² / P₂

il vient : P₂ = P₁ (R₂ / R₁)²

Il nous reste à calculer le rayon avant contraction, et nous en déduirons la période recherchée.

Dans chaque cm³, il y a 10¹⁰ atomes d’hydrogène, de masse 1,6734 10^-24 g chacun. Ce qui fait une masse volumique de :

ρ = 10¹⁰ 1,6734 10^-24 g cm^-3 = 1,6734 10^-14 g cm^-3

Le nuage est une sphère de rayon R₁, qui a donc un volume V = 4/3 π R₁³, et une masse de M = ρ V = ρ 4/3 π R₁³.

On a supposé que sa masse était une masse solaire, donc 2 10³³ g. On peut donc écrire :

2 10³³ = M = ρ 4/3 π R₁³ = 1,6734 10^-14 4/3 π R₁³ = 7,009 10^-14 R₁³

d’où :

R₁³ = 2 10³³ / 7,009 10^-14 = 0,29 10⁴⁷ cm³

Il suffit d’extraire la racine cubique :

R₁ = (0,28 10⁴⁷)^-3 cm = (28 10⁴⁵)^-3 cm = 3 10¹⁵ cm = 3 10¹³ m = 30 milliards de km.

Six fois la distance de Pluton au Soleil.

Nous avons maintenant : P₁ = 1.000 ans, R₁ = 3 10¹³ m, et le rayon actuel du Soleil est R₂ = 7 10⁸ m. Donc :

P₂ = P₁ (R₂ / R₁)² = 1.000 ans ( 7 10⁸ / 3 10¹³)² = 1.000 × 5,44 10^-10 années = 5,44 10^-7 années

Multiplions cette valeur par 365, puis par 24, puis par 60 et encore par 60, pour l’écrire en secondes : P₂ = 17 secondes !

Même si les données choisies pour le calcul ne sont pas parfaitement exactes, l’erreur ne peut justifier un écart entre 17 secondes et un mois (rapport de 150.000), comme on l’observe. Remarquons de plus que nous avons omis le disque de matière qui reste autour de l’étoile naissante en supposant que la totalité du disque s’effondrait.

Il est évident qu’un mécanisme a dû freiner la rotation du Soleil, et la théorie de sa formation devra en tenir compte. Les vitesses de rotation des autres étoiles sont du même ordre de grandeur, à un facteur 100 près, et doivent justifier elles aussi de ce mécanisme. On sait que le moment cinétique de rotation du Soleil a été transféré aux planètes, qui en possèdent aujourd’hui 98 %.

On explique ce phénomène par l’existence d’un champ magnétique, dont les lignes partent du Soleil, et vont vers l’extérieur. Les planètes sont prises dans ce champ, et interagissent avec lui. Le champ leur communique de l’énergie, qu’il emprunte au Soleil. C’est ainsi que le Soleil ralentit et les planètes s’éloignent un peu.

6.6 Masse volumique

On ne peut pas parler simplement de la masse volumique d’une étoile. L’étoile n’a pas de limite précise, et se dilue progressivement dans l’espace à partir de ce qu’il est convenu d’appeler sa surface (la photosphère). En pénétrant dans son intérieur, on observerait une masse volumique régulièrement croissante vers le centre.

On peut donc parler de plusieurs masses volumiques différentes :

•  la masse volumique centrale, la plus forte, celle qui autorise les réactions thermonucléaires ;
•  la masse volumique moyenne, obtenue en divisant la masse totale de l’étoile par son volume total ;
•  la masse volumique en un point quelconque, à la distance r du centre.

La dernière n’est utilisée que pour construire des modèles d’étoiles. Dans ce cas, il faut définir précisément la variation de la masse volumique en fonction de la distance au centre, pour savoir où exactement se produisent les réactions.

Pour se faire une idée globale d’une étoile, la masse volumique moyenne semble la plus représentative, alors que pour déterminer sa production d’énergie, c’est la masse volumique centrale qui est décisive. Pour les étoiles de très faible masse, les deux sont proches : la gravité étant faible, la matière se réparti relativement uniformément dans le globe de l’étoile. Mais pour les étoiles très massives, la très forte gravité produit au contraire une grande concentration de matière au centre, avec une masse volumique très élevée, alors que les couches externes de l’étoile sont soumises à une température si forte qu’elles se dilatent démesurément. La masse volumique centrale est extrêmement élevée, et la masse volumique moyenne très basse à cause du rayon immense du globe.

Masse volumique moyenne de trois types d’étoiles :

•  Soleil : 1 g / cm³
•  naine blanche : 10⁹ g / cm³
•  étoile à neutrons : 10¹⁴ g/cm³
•  géante rouge : de l’ordre de 10^-6 g/cm³

Un seul cm³ d’étoile à neutrons a la même masse qu’un cube de granite de 333 m de côté !

Ou bien un petit volcan de pouzzolane ayant la silhouette du Fuji Yama, de 500 m de haut !

6.7 Diagramme HR

Nommé d’après les deux astronomes qui l’ont proposé, indépendamment l’un de l’autre : Ejnar Hertzsprung et Henry Norris Russel. Le diagramme HR montre la relation existant entre la température superficielle d’une étoile et sa luminosité totale. Ce diagramme, qui peut paraître semblable à beaucoup d’autres, est en fait l’outil fondamental de l’astrophysique.

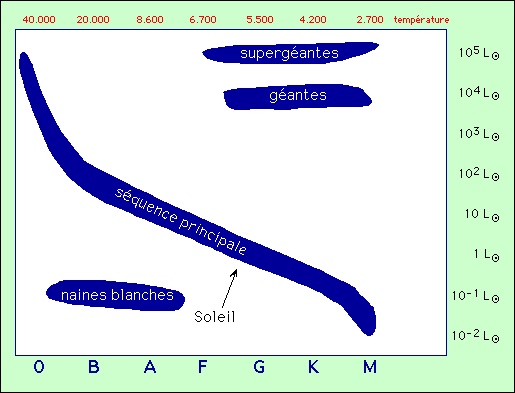
Le diagramme HR est à deux dimensions, avec en abscisse (axe horizontal) une indication de la température de l’étoile. Trois valeurs équivalentes sont possibles :

•  le type spectral ;
•  la température effective ;
•  l’indice de couleur.

Un examen rapide du tableau des types spectraux vous convaincra que ces trois éléments sont équivalents, le tableau permettant de passer simplement de l’un à l’autre.

L’axe des ordonnées (vertical) est gradué selon la luminosité de l’étoile, mais on peut aussi y mettre la magnitude absolue, ce qui est équivalent. Vous trouverez dans la littérature des diagrammes HR construits avec diverses combinaisons de ces quantités.

6.8 Les populations stellaires

Le diagramme HR permet de classer les étoiles (de notre Galaxie) en deux types de populations :

•  population I, comprenant des étoiles jeunes, dont la métallicité est forte (jusqu’à 2 %, valeur qui représente la métallicité du Soleil). Elles se trouvent essentiellement dans les bras spiraux de la Galaxie, noyées dans la matière interstellaire.
•  population II, constituée d’étoiles vieilles à métallicité beaucoup plus faible. Elles ne se trouvent pas dans les bras spiraux. Les géantes rouges et les naines blanches font partie de la population II. Les amas globulaires sont de population II exclusivement, ainsi que les galaxies elliptiques.

Pour un âge global donné, une population stellaire apparaît d’autant plus bleue que sa métallicité est plus élevée.

La métallicité dans les atmosphères stellaires entraîne un effet de serre ! Celui-ci est d’autant plus important que l’étoile est plus froide. Il joue donc un rôle dans les étoiles de faible masse.

On parle quelquefois de population III, pour classer des étoiles de métallicité quasiment nulle. De telles étoiles seraient vraiment très vieilles, formées juste après le Big Bang.

La composition globale des étoiles est de 90 % d’hydrogène (en nombre d’atomes), et 10 % d’hélium (tout le reste ne représente que 0,1 % des atomes présents dans les étoiles). Attention, on donne souvent la répartition sous la forme 74 % H pour 24 % He (2 % métaux). Lorsqu’on donne sous cette forme, il s’agit du pourcentage en masse. L’atome d’hélium étant 4 fois plus lourd que celui d’hydrogène, ces deux formulations sont équivalentes.

7 Equilibre

7.1 Antagonisme

Vous pourrez trouver des explications synthétiques sur la vie des étoiles,

L’équilibre d’une étoile se réalise entre deux forces antagonistes :

•  la gravité qui la comprime ;
•  une pression interne qui la dilate.

On nomme cet équilibre équilibre hydrostatique.

La gravité est due à la présence de la matière, donc elle est permanente.

La pression due à l’énergie n’est que transitoire ; lorsque la source d’énergie est épuisée, elle cesse. Par contre, la pression d’origine quantique est permanente, comme la gravité. Donc, tout équilibre induit par l’énergie est provisoire (pouvant atteindre des centaines de milliards d’années tout de même…), alors que l’équilibre quantique sera, s’il est atteint, définitif (en l’absence d’intervention extérieure).

C’est l’énergie qui produit la pression dans toutes les étoiles que nous observons ; C’est son effet que nous allons considérer maintenant.

L’énergie s’échappe de l’étoile, puisque nous en recevons. Les pertes se font par deux mécanismes :

•  le rayonnement ;
•  les pertes neutriniques.

Les pertes neutriniques sont négligeables, sauf dans certaines phases particulières où elles deviennent prépondérantes pendant un temps très bref. On considère, dans ce qui suit, que la perte est due au rayonnement.

L’étoile perdant de l’énergie, elle doit en produire en permanence pour maintenir l’équilibre. Ceci ne peut donc durer qu’un temps fini.

Cette énergie a deux origines possibles :

•  gravitationnelle ;
•  nucléaire.

L’énergie gravitationnelle est produite par la contraction de l’étoile. Or le diamètre ne peut diminuer indéfiniment, au moins à une vitesse significative. Donc la production d’énergie gravitationnelle est limitée dans le temps.

L’énergie nucléaire provient de la transformation d’un élément chimique en un autre (hydrogène en hélium, ou bien hélium en carbone, ou bien …). Lorsque le premier est épuisé, la production d’énergie cesse.

Les deux mécanismes de production d’énergie à la disposition d’une étoile (gravitationnelle et nucléaire) ayant une durée limitée, les étoiles évoluent nécessairement.

Les réactions nucléaires requièrent des conditions de température et de pression élevées. Ce sont des réactions de fusion (fusion de deux atomes pour en produire un nouveau). Chaque élément chimique fusionne dans des conditions de température et de pression différentes, croissantes avec la masse de l’atome. L’hydrogène fusionne à la température la plus basse (seulement une dizaine de millions de degrés) ; à température et pression plus élevées fusionne l’hélium ; puis le carbone…

Le schéma ci-dessous représente l’équilibre dans les étoiles, entre gravité et pression. La pression est due à une production d’énergie ou à un mécanisme quantique (flèches côté droit). L’énergie est d’origine gravitationnelle ou nucléaire, et dans ce dernier cas due à la fusion des divers éléments. Sur le côté gauche, sont indiquées les pertes d’énergie, par rayonnement ou par émission de neutrinos.

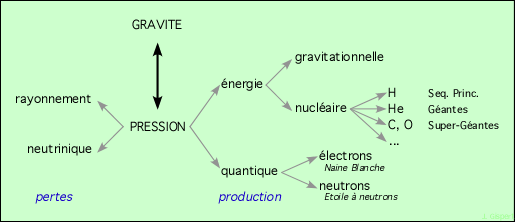
Suivez le chemin : rayonnement, pression, énergie, gravitationnelle ; vous venez de définir une étoile naissante, qui n’est pas encore en équilibre (l’énergie gravitationnelle est produite par la contraction de l’étoile, dont le diamètre diminue au cours du temps). C’est une étoile de type T Tauri.

Suivez maintenant le chemin : rayonnement, pression, énergie, nucléaire, H ; vous venez de définir une étoile typique comme le Soleil (de la Séquence Principale).

La production d’énergie peut être en même temps d’origine nucléaire et gravitationnelle, mais l’étoile alors n’est pas en équilibre (puisqu’elle se contracte...). Ceci se produit pendant un temps bref, entre deux phases stables. Par exemple dans l’ascension vers la branche des géantes.

Les phases d’équilibre sont longues, les phases de transition hors équilibre brèves.

L’évolution d’une étoile se fait, sur ce graphique, de heut en bas : lors de sa formation, la production d’énergie est gravitationnelle ; ensuite, elle est nucléaire (fusion de l’hydrogène, puis de l’hélium...) ; enfin, elle est quantique (naines blanches et étoiles à neutrons). Le cas des trous noirs est un équilibre très particulier, dont on ignore à peu près tout...

Les pertes neutriniques sont peu importantes dans la vie normale d’une étoile, et ne se montrent efficaces que pendant de brefs instants particuliers. Les pertes peuvent se faire à la fois par rayonnement et par neutrinos. Là encore, l’étoile n’est pas stable, car la perte neutrinique se fait sans contre-partie, les neutrinos emportant leur énergie pratiquement sans interaction avec la matière de l’étoile… sauf dans le cas où la densité est extrêmement élevée, c’est-à-dire dans le cœur d’une supernova en cours d’effondrement. C’est aussi là que les neutrinos sont produits dans la plus grande abondance.

L’énergie gravitationnelle n’intervient dans la vie de l’étoile que lorsque l’énergie d’origine nucléaire fait défaut :

•  lors de la formation de l’étoile, encore trop froide pour les réactions de fusion. La contraction gravitationnelle chauffe le gaz progressivement. Une partie de l’énergie produite est rayonnée, l’autre maintient un pseudo-équilibre (pseudo puisque l’étoile se contracte) ;
•  lorsque le combustible nucléaire est épuisé, induisant une baisse des réactions et donc de l’énergie. L’équilibre n’est plus assuré, et la gravitation l’emporte à nouveau. L’étoile se contracte, donc se chauffe, et de nouvelles réactions peuvent éventuellement se produire.

Les diamètres mis en italique sont indicatifs, et correspondent à des objets d’une masse solaire à peu près.

Une étoile de la Séquence Principale brûle son hydrogène jusqu’à 1/5^e de la quantité initiale. En effet, la température suffisante pour cette fusion n’est atteinte que dans le cœur, l’enveloppe étant de ce point de vue, inerte.

La densité moyenne des étoiles est extrêmement variable de l’une à l’autre : celle des naines blanches vaut 50.000 fois la densité de l’eau, le Soleil 1,4 g/ cm³, Antarès a une densité moyenne plusieurs millions de fois plus faible que celle de l’eau.

90 % des étoiles sont sur la Séquence Principale ; c’est parce que cette période de leur vie est la plus longue.

7.2 Chaîne proton-proton :

H + H → ²H + e⁺ + ν + γ

²H + H → ³He + γ

³He + ³He → ⁴He + 2H + γ

La première réaction est très très lente (10¹⁰ ans ! ) ; c’est pourquoi la durée de vie du Soleil est si grande (détails dans le chapitre réactions nucléaires).

Lithium, Bérylium et Bore, fragiles, se désintègrent au fur et à mesure de leur production.

7.3 Cycle CNO

Le cycle du carbone, ou cycle CNO (Carbone, Oxygène) ou cycle de Bethe, est décrit en détails dans la page consacrée à la physique nucléaire. C’est un autre ensemble de réactions nucléaires qui fusionne l’hydrogène en hélium, mais qui se distingue des chaînes PP par certains aspects.

7.4 Dépendance à la température

La chaîne PP1 (exposée ci-dessus) présente son maximum d’efficacité à la température la plus basse possible pour la fusion de l’hydrogène. Il existe deux variantes. La variante PP2 est plus efficace à une température légèrement plus élevée, et la variante PP3 encore un peu plus. Le cycle CNO trouve son efficacité maximale à une température nettement plus élevée.

La température optimale n’est pas le seul élément à considérer. La dépendance du taux de réactions par rapport à la température est au moins aussi importante. Les réactions de la chaîne PP dépendent de la température. Si celle-ci augmente un peu, la production d’énergie augmente un peu également. Il s’ensuit une augmentation de pression, qui dilate légèrement l’étoile. La dilatation entraîne une baisse de la température, et par suite le taux de réactions diminue, et la température avec. Toute augmentation de température est donc annulée par un mécanisme antagoniste, et cette dépendance produit la grande stabilité des étoiles sur la Séquence Principale.

Le cycle CNO dépend beaucoup plus fortement de la température. Or celle-ci diminue lorsqu’on s’éloigne du centre. Donc, le taux de réactions produites par le cycle CNO diminue beaucoup plus vite avec l’éloignement du centre, que celui de la chaîne PP. Ceci a deux conséquences :

•  les étoiles PP ont un cœur beaucoup plus gros, et la température y diminue lentement avec la distance au centre ;
•  dans les étoiles CNO, la température diminue très vite avec l’éloignement du centre, et le transport radiatif ne suffit plus : le cœur est convectif.

Les étoiles PP sont les moins massives (température centrale plus basse), qui occupent le bas de la Séquence Principale. Donc, dans le bas de la Séquence Principale, les étoiles ont un cœur radiatif, et une enveloppe convective ; c’est l’inverse dans la Séquence Principale supérieure.

7.5 Rendement comparé

A basse température, au-dessous de 10 millions de degrés, le cycle proton-proton présente un bon rendement, et le cycle CNO n’a pas la température suffisante pour produire beaucoup d’énergie. Lorsque la température augmente, les rendements s’inversent, et le cyclo CNO devient prépondérant. Le schéma ci-dessous montre l’efficacité des deux cycles, et la courbe résultant de leur combinaison :

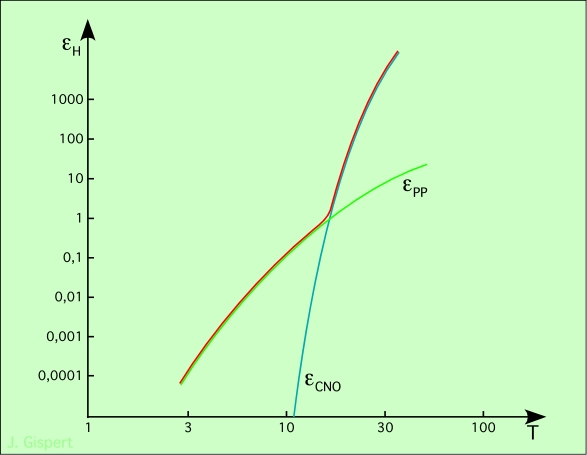
Par conséquent, puisque la température centrale dépend de la pression, qui dépend de la masse, les étoiles les moins massives fusionnent essentiellement par le cycle PP (courbe verte), les plus massives par le cycle CNO (courbe bleue). Pour le Soleil, la masse est juste en-dessous du coude, et le cycle PP est prépondérant. La courbe rouge est la résultante des deux, qui s’applique dans une étoile réelle où les deux cycles coexistent.

Remarquez sur les courbes la sensibilité des deux mécanismes à la température : la courbe ε_PP est moins pentue que la courbe ε_CNO. Ceci montre que pour une petite élévation de température, le taux de réactions CNO augmente beaucoup plus que le taux PP. Par conséquent, le surcroit d’énergie produite par une petite élévation de température est plus grand dans le cycle CNO, et la pression augmente plus vite. Cette augmentation entraîne immédiatement une augmentation du volume (dans un gaz parfait, cas général), et donc une baisse de température. C’est ce mécanisme qui régule le fonctionnement des étoiles, mais lorsque la sensibilité à la température est trop grande, il peut aussi produire des instabilités.

7.6 Séquence Principale

Gravité relativement faible ⇒ production d’énergie faible ⇒ grande longévité.

Revenons au Soleil. Grâce à des mesures de l’assombrissement au bord, on sait que la température dans la photosphère diminue lorsque l’altitude croît, de 5.700 K à 1.200 K seulement (soit 5.973 °C ≈ 6.000 °C, à 1.473 °C ≈ 1.500 °C). Mais au-dessus, elle remonte, et la chromosphère est presque toute à 7.000 K (la chromosphère a une épaisseur de l’ordre de 3.000 km).

A la limite entre la chromosphère et la couronne, sa température croît brutalement jusqu’à un million de degrés. La température moyenne de la couronne est de 2 millions de K ; Elle est très irrégulière, et monte jusqu’à 5 millions de K.

La chromosphère et la couronne sont trop peu denses pour absorber le rayonnement. C’est pourquoi leur température peut être très élevée (elles ne se comportent absolument pas comme des corps noirs). Au lieu de présenter des raies d’absorption, elles donnent des raies d’émission ; en particulier pour la chromosphère, la raie Hα largement dominante lui donne sa couleur rouge caractéristique.

Outre les raies de l’hydrogène et de l’hélium, on observe celles des métaux fortement ionisés (Fe XIV).

La couronne étant très chaude, émet dans les très courtes longueurs d’onde. Elle est particulièrement visible en rayons X (bien sûr au-delà de l’atmosphère qui les absorbe). C’est ainsi que les satellites observant dans cette gamme ont montré une couronne agitée, et très inégale. Des boucles de matière et des trous, qui n’apparaissent pas dans le domaine visible, montrent que les champs magnétiques sont très intenses. Ce sont eux qui sont responsables du chauffage de la couronne à si haute température.

Mira : découverte en 1596 géante rouge variable de type spectral M, période de 330 jours ; sa taille varie de 50% et sa luminosité de 7 magnitudes, soit 600 fois.

7.7 Naines brunes

Lorsqu’un nuage protostellaire en contraction est de masse insuffisante, inférieure à 0,08 M, la gravitation restera trop faible pour élever la température centrale jusqu’aux 10 millions de degrés fatidiques (approximativement), permettant l’allumage des réactions nucléaires. Toutefois, si on observe attentivement la série de réactions nucléaires qui mènent à la synthèse de l’hélium, on distinguera la première, qui à partir de deux noyaux d’hydrogène donne un noyau de deutérium (fusion de deux protons, et désintégration béta de l’un d’eux en neutron). C’est elle qui réclame la température la plus élevée. Les réactions suivantes, qui utilisent le deutérium comme combustible, se produisent à température plus basse. Or il en existe dans l’Univers une petite proportion, qui a été produite dans ses premiers instants (par la réaction p + p). Cette petite quantité de deutérium va pouvoir fusionner dans une étoile de très faible masse, et produire un peu d’énergie.

Ainsi, les objets stellaires les plus petits auront une faible source d’énergie nucléaire. Elles pourront briller faiblement, et ce sont des étoiles… Mais rien à voir avec les vraies étoiles de la Séquence Principale. Leur surface restera relativement froide, donc très peu lumineuse. Comme d’autre part elles ont un très faible diamètre, elles rayonnent très peu. Ce sont des astres très difficiles à détecter.

Une première naine brune a été observée il y a quelques années, il s’agit de Gliese 229 B (Gliese 229 s’est avérée être une étoile double). Sa luminosité vaut à peu près 0,000006 fois la luminosité du Soleil. De plus, son spectre présente des raies moléculaires, en particulier du méthane. La molécule de méthane ne peut exister dans une atmosphère stellaire normale, à cause de la trop forte température. C’est une indication indirecte de la basse température de la naine brune.

photo HST

On a accordé récemment un grand intérêt aux naines brunes parce que, en grand nombre, elles pourraient représenter une partie de la masse manquante dans les galaxies. Aussi des programmes de recherches systématiques ont été mis sur pied. Si une naine brune sombre et proche passe devant une étoile, par effet de micro-lentille gravitationnelle, elle devrait amplifier la lumière de l’étoile pendant un bref moment. Et effectivement, on a observé une dizaine d’événements qui pourraient s’expliquer de cette manière, mais leur nombre est beaucoup plus faible que ce qu’on attendait en regard du problème posé. Apparemment, les naines brunes n’expliquent pas la masse manquante de notre Galaxie.

Si on considère des naines brunes de masse de plus en plus faible, on trouvera une limite en dessous de laquelle même la combustion du deutérium n’est plus possible. Il ne s’agit donc plus d’une étoile, mais d’une planète. On peut donc envisager l’existence de planètes formées à la manière d’une étoile, à partir de la contraction d’un nuage d’hydrogène et non d’un disque d’accrétion entourant une jeune étoile. Un objet candidat de ce type a été découvert dans le Taureau, mais il pourrait s’agir d’une planète formée normalement et éjectée de son étoile par les perturbations dues aux autres planètes.

Finalement, on peut voir une continuité des masses entre les plus petites planètes, et les plus grosses étoiles. Mais il existe bien une limite de nature, puisque les premières n’ont pas d’énergie nucléaire, au contraire des secondes.

7.8 Equilibre hydrostatique

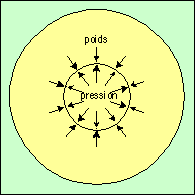Le problème qui se pose maintenant est de savoir pourquoi le Soleil ne change pas d’aspect : il pourrait se contracter, ou se dilater, rayonner plus ou moins selon les époques. En fait, il est dans un équilibre remarquable, ce dont les modèles doivent tenir compte. Cet équilibre entre le poids d’une couche supérieure et la pression que lui oppose celle sur laquelle elle repose se nomme équilibre hydrostatique. Si l’équilibre existe, le poids est exactement compensé par la pression. C’est parce que le Soleil est en équilibre hydrostatique qu’il ne grossit pas, et ne maigrit pas. D’où vient la pression qui équilibre le poids ? dans le cas de la Terre, il s’agit tout simplement de la rigidité des roches, qui sont des solides. Mais pour le Soleil, constitué de gaz, il n’y a pas de rigidité, il faut donc un autre mécanisme.

Considérons le Soleil comme une succession de couches que l’on rencontrerait en s’enfonçant à l’intérieur. Pour comprendre l’équilibre, faisons une expérience : plaçons un livre à plat sur une table. Le livre s’appuie sur la table, sur laquelle il repose. Son poids le fait descendre vers le bas, mais la présence de la table l’en empêche. Le poids du livre écrase la table, qui réagit en exerçant une pression sur lui. Un équilibre s’établit, et le livre ne bouge plus.

Si maintenant on pose un presse-papier sur le livre, son poids écrase ce dernier, qui oppose une pression au poids du presse-papier ; un nouvel équilibre s’établit.

7.9 Pression

Représentons-nous un gaz comme un ensemble d’atomes qui s’agitent en tous sens. S’ils s’agitent, c’est qu’ils possèdent de l’énergie ; il s’agit de l’énergie thermique (dues à la chaleur). Un atome qui tombe vers le centre du Soleil va très vite heurter un autre atome qui s’en échappe rapidement à cause de cette énergie. Sous le choc, sa chute s’arrête.

Nous venons d’expliquer pourquoi les atomes ne tombent pas vers le centre du Soleil, mais en tenant compte de l’énergie qu’ils possèdent. Or le Soleil rayonne, ce qui est pour lui une perte d’énergie. Il faut donc une production d’énergie pour entretenir l’équilibre.

Cette énergie est la lumière et la chaleur que le Soleil rayonne. Mais d’où provient-elle ?

Maintenant, nous pouvons donner une définition d’une étoile :

c’est une sphère de gaz :

• auto gravitante,
• en équilibre hydrostatique

L’équilibre est entretenu par un gradient de pression, lui-même entretenu par un gradient de température, produit par la chaleur engendrée par les réactions nucléaires centrales.

Gradient signifie variation. Le gradient de pression est une baisse progressive de la pression lorsqu’on s’éloigne du centre.

7.10 Energie gravitationnelle

Si vous laissez tomber un objet pesant sur un parquet, il y laissera une marque ; ceci prouve qu’il possédait de l’énergie. Il l’a acquise dans sa chute, puisqu’il n’en avait pas lorsque vous le teniez dans la main. (attention, il ne possédait pas d’énergie cinétique, celle due au mouvement ; mais il possédait de l’énergie potentielle, qui en se transformant lui donne l’énergie cinétique) C’est donc la gravité de la Terre qui, en l’attirant à elle, lui a communiqué cette énergie. Tout atome d’hydrogène, en tombant vers le centre du Soleil, dégagera donc aussi de l’énergie ; on la nomme énergie gravitationnelle. Elle peut expliquer la brillance du Soleil au rythme que l’on observe, mais au prix d’une lente contraction du Soleil sur lui-même. Son diamètre devrait diminuer. Ce n’est pas le cas, et donc cette source ne convient pas pour expliquer son fonctionnement.

Une étoile est une boule de gaz (hydrogène et hélium), qui tient rassemblée par sa propre gravité. La densité décroît du centre vers la périphérie, jusqu’à devenir nulle très loin (dans le milieu interstellaire). Une étoile n’a pas de surface solide comme une planète, elle n’a même pas de surface du tout ! il existe une étoile que l’on peut voir de près, le Soleil. Or l’expérience quotidienne nous montre que le Soleil est bien rond. Comment expliquer cette apparence bien nette, avec la dilution progressive, continue, du gaz que nous avons envisagée ? Nous verrons la réponse un peu plus loin, en étudiant sa structure.

7.11 Nature des étoiles

Les étoiles sont de grandes masses de gaz. Les atomes qui se trouvent à la surface d’une étoile sont très fortement attirés vers le centre par la forte gravité de l’astre. Ils ont donc tendance à tomber. Si tous les atomes suivaient ce penchant, l’étoile se contracterait progressivement (en fait, très rapidement), jusqu’à une taille minuscule.

Puisque ce n’est pas le cas, une force doit agir, qui a tendance à dilater l’étoile. Et sa stabilité provient d’un subtil équilibre entre ces deux forces. Les origines de cette force sont différentes selon l’âge de l’étoile.

Les gaz qui les composent sont essentiellement l’hydrogène et l’hélium, les autres éléments n’étant présents qu’en très faibles proportions (c’est la spectroscopie qui nous l’indique).

Il existe des étoiles de brillance, de couleur, de dimensions très différentes. Leurs distances à la Terre sont très diverses, bien que toutes celles qu’on distingue à l’œil nu soient en fait très proches de nous (astronomiquement parlant).

7.12 Intervalles de définition des étoiles

•  la limite inférieure de la masse correspond à une température centrale juste suffisante pour permettre la fusion de l’hydrogène. Elle est définie par les propriétés physiques de l’hydrogène, et par la gravitation. Au-dessous de cette limite, la fusion du deutérium (hydrogène lourd) est possible. Mais cet isotope est rare, et la production d’énergie restera très faible. Les objets dont la masse est comprise entre 0,01 et 0,08 M sont des naines brunes : on qualifie ainsi des étoiles qui possèdent une source d’énergie propre par le deutérium, mais qui sont incapables de fusionner l’hydrogène. Au dessous de 0,01 M, ce sont des planètes (aucune production d’énergie nucléaire).
•  la limite supérieure est beaucoup moins bien définie, car elle dépend de nombreux paramètres. En fait, rien n’interdit la formation d’étoiles beaucoup plus massives que 60 M, mais le débordement d’énergie nécessaire pour éviter leur écrasement gravitationnel est tel, qu’elles sont instables  : les couches extérieures sont violemment expulsées. Un bel exemple nous est donné par η Carinæ, qui atteint 150 M.

7.13 Fin de la Séquence Principale

Comme son nom l’indique, la Séquence Principale est la phase de plus grande stabilité d’une étoile. C’est la fusion de l’hydrogène seule qui peut lui procurer cette stabilité, aussi la Séquence Principale est-elle la phase pendant laquelle l’étoile fusionne l’hydrogène en son cœur.

Elle finit lorsque les réactions de fusion s’arrêtent au centre, qui se contracte, mais les réactions se propagent vers l’extérieur, et continuent dans une couche autour du centre. Cette couche va peu à peu s’éloigner du centre, à mesure que l’hydrogène est transformé en hélium.

La fin de la Séquence Principale est le début de l’ascension vers la branche des géantes. A mesure que les réactions s’éloignent du centre, le cœur se comprime, sa température augmente donc, il chauffe davantage les couches qui le surmontent. Celle-ci se dilatent donc, et l’enveloppe de l’étoile grossit. Sa surface augmente, et il s’ensuit une baisse de la température superficielle, qui se traduit par un rougissement.

De plus, les atomes qui se trouvent à la périphérie de l’enveloppe se trouvent de plus en plus loin du centre.

Pendant l’ascension vers la branche des géantes, l’étoile n’est pas vraiment en équilibre. Elle se déplace rapidement sur le diagramme HR vers le haut et la droite. La fin de cette ascension dépend de la masse de l’étoile.

7.14 Amas d’étoiles

On peut voir dans le ciel des regroupements serrés d’étoiles. Les Pléiades en sont un bel exemple, visible dans le ciel du soir au début de l’hiver. Elles ressemblent à une constellation en miniature. Non loin des Pléiades se trouvent les Hyades dans le Taureau. Ces deux groupements sont appellés amas.

On peut voir des amas d’aspect différent : c’est le cas de M13 dans Hercule. Il se présente sous une forme sphérique, avec un centre très brillant qui forme une tache lumineuse. A la périphérie, on distingue des étoiles, qui se raréfient en s’éloignant du centre. Ces amas d’aspect différent ont pris le nom d’amas globulaires, en rapport avec leur aspect.

Ces deux types d’amas trahissent des natures profondément différentes, que nous verrons en détail dans un chapitre particulier.

8 Perte de masse

8.1 Vent stellaire

Le Soleil perd en permanence des atomes, qu’il éjecte à grande vitesse dans l’espace. Ce sont essentiellement des noyaux d’hydrogène, avec un peu d’hélium. Pourtant, il est dans sa phase tranquille de la Séquence Principale. Au stade T Tauri, l’étoile produit énormément d’énergie gravitationnelle, elle est très brillante et émet un fort vent stellaire. Celui-ci est mesuré par effet Doppler, la vitesse d’éjection élargissant les raies d’absorption.

Dans la phase qui suit la Séquence Principale, qui voit l’ascension vers la branche des géantes, l’enveloppe grossit considérablement, et les atomes qui se trouvent à sa périphérie sont de moins en moins liés par la gravitation, qui diminue avec la distance. De ce fait, ils s’échappent beaucoup plus facilement, ce qui produit un renforcement considérable de vent stellaire. Dans les étoiles de grande masse, il atteint les 10^-4 M par an, contre 10^-13 M actuellement pour le Soleil.

Dans le cas des étoiles de grande masse, le vent stellaire enlève plus de la moitié de la masse originale de l’étoile, avant qu’elle n’explose en supernova.

Le vent stellaire est une perte de masse continue. C’est une émission de particules.

L’intensité du vent stellaire dépend de la métallicité

L’évolution des étoiles dépend fortement de la perte de masse dans plusieurs phase de leur vie. L’évolution des étoiles massives dans une galaxie de faible métallicité (vieille) peut être radicalement différente de l’évolution des étoiles dans notre Galaxie.

8.2 Taux de perte de masse

(masse perdue par unité de temps).

≥ 0 est exprimée en masses solaires par an.

Une étoile pour laquelle = 10^-6 M /an perd une masse égale à celle de la Terre en 3 ans.

8.3 Vitesse terminale

C’est la vitesse du vent stellaire à grande distance de l’étoile (où la gravité est faible).

V_t = 10 km s^-1 pour les supergéantes froides, 3.000 km s^-1 pour les étoiles chaudes lumineuses.

C’est une vitesse d’ensemble ; ce n’est pas la vitesse d’agitation thermique des atomes dans le vent.

• une étoile de élevée n’évoluera pas comme une étoile de faible ;
• des théories différentes donnent des valeurs différentes pour et V_t. Ces valeurs permettent donc de départager les théories.

Le taux de perte de masse est la masse qui traverse une sphère de rayon r centrée sur l’étoile, pendant une unité de temps. La densité à la distance r est ρ(r), la vitesse V(r).

C’est la même quantité qui traverse toute sphère de rayon r centrée sur l’étoile.

9 Formation des raies spectrales dans le vent stellaire

9.1 Processus Line-scattering

Un photon est absorbé, puis réémis en un temps très bref. Il est de même couleur, au décalage Doppler dû à l’agitation thermique près. Si le niveau concerné est proche du fondamental, le temps de désexcitation est très souvent 10^-10 à 10^-9 s.

Si le niveau de base est le fondamental, on dit qu’il s’agit d’une raie de résonnance. C’est l’origine de la plupart des profils P Cygni.

9.2 Recombinaison

Un ion rencontre un électron, qui s’attache à lui. Souvent au niveau fondamental, parfois dans un niveau excité. Il s’ensuit une cascade vers le niveau fondamental, avec émission de photons.

Ce mécanisme est responsable des raies d’émission Hα et des raies d’émission IR dans les vents stellaires des étoiles chaudes.

9.3 Excitation par chocs

Un choc peut fournir à un atome l’énergie d’excitation. Ensuite, il se désexcitera en émettant des raies.

9.4 Absorption pure

Photo excitation d’un atome déjà excité. La transition résultant de la première excitation est perdue. Très peu important dans les vents stellaires, car les atomes sont presque tous au niveau fondamental.

9.5 Maser

MASER est un acronyme pour Microwave Amplification of Stimulated Emission of Radiation. C’est un mécanisme assez semblable à l’effet LASER (Light Amplification of Stimulated Emission of Radiation), mais dans un domaine de longueurs d’ondes différent (micro ondes).

Un atome excité à un niveau peut produire un photon ν, s’il reçoit un photon de même fréquence ν. Il se désexcite en émettant un photon ν dans la même direction  ! On a alors deux photons identiques qui se déplacent dans la même direction. Chacun de ces photons peut à sont tour provoquer l’émission d’un autre, d’où l’effet d’amplification.

Si la proportion d’atomes excités est grande, ce phénomène est important. Il ne doit pas y avoir de gradient de vitesse, car l’effet Doppler inhibe ce mécanisme.

Le mécanisme Maser produit des raies fortes et étroites (pas de décalage Doppler) dans les vents des étoiles froides.

10 Maquette d’étoiles

Envisageons de dessiner à la même échelle sur une feuille de papier une étoile à neutrons, une naine blanche, le Soleil (Séquence Principale) et une géante rouge. Combien de feuilles A4 nous faut-il ?

Le rayon typique d’une étoile à neutrons est de 10 kilomètres. Celui d’une naine blanche est du même ordre que celui de la Terre, c’est-à-dire de 10.000 km ; le rayon du Soleil est de 740.000 km, et enfin celui d’une géante rouge atteint 200 millions de km.

Si nous représentons l’étoile à neutrons par un cercle de 1 mm de diamètre (tête d’épingle en verre), les diamètres des autres types seront (1 mm correspondant à 10 km) :

Et pourtant, elles ont toutes presque la même masse…

La surface du cercle qui représente la géante rouge est de π r² = π 10² km² = 314 km².

Transformons cette valeur en mètres carrés : 1 km = 1.000 m ⇒ 1 km² = 10⁶ m². La surface de la géante rouge est donc 314 × 10⁶ m²

Une feuille A4 mesure 21 × 29,7 cm, sa surface est 0,21 × 0,297 = 0,062 m² ; le nombre de feuilles à juxtaposer pour pouvoir dessiner la géante rouge est de 314 10⁶ / 0,062 = 5.064 10⁶. C’est à dire 5 milliards de feuilles !!

Combustion du carbone au-dessus de 2,25 Mo.

11 Etoiles doubles et étoiles variables

Les étoiles doubles sont des étoiles qui nous semblent très proches l’une de l’autre, ou qui le sont réellement. On les étudiera par ailleurs.

Certaines étoiles présentent des variations d’intensité lumineuse. On les nomme étoiles variables. De très nombreux mécanismes sont responsables de ces variations, et un chapitre entier leur est consacré. La compréhension des étoiles variables est fondamentale pour l’astrophysique.

---=OO=---