Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Etoiles doubles | |||||||
Les étoiles doubles sont des couples d’étoiles, apparents ou réels.
Selon les moyens observationnels, on distingue quelques types d’étoiles doubles :
Ce classement n’a aucune signification physique, puisqu’il est basé uniquement sur les différentes méthodes d’observation. Mais les propriétés physiques sont corrélées avec ces méthodes. Aussi, savoir qu’une étoile appartient à telle ou telle catégorie donne une information immédiate sur les propriétés accessibles, et font la pertinence de ce classement.
Ce sont des étoiles proches l’une de l’autre dans le ciel, par effet de perspective. Les étoiles occupent dans le ciel des positions aléatoires, car leur répartition est tout à fait quelconque. Il arrive quelquefois que deux étoiles se trouvent avoir une direction très voisine, alors que leurs distances sont assez différentes. Par effet de perspective, elles nous paraissent proches l’un de l’autre.
De tels couples n’ont aucun intérêt sur le plan scientifique. Cependant, si un véritable couple (deux étoiles à très courte distance l’une de l’autre) est proche de la Terre, il peut être vu sous un aspect exactement semblable. Pour savoir si un tel couple visuel est dû à la perspective, il faut déterminer les distances des deux composantes.
Les doubles vraies sont des couples d’étoiles liées par la gravité. Elles tournent autour de leur centre de gravité commun.
Contrairement à ce que l’on a cru très longtemps, les étoiles doubles ne sont pas l’exception, mais la règle. Plus précisément, plus de 50 % des étoiles appartiennent à un système multiple, double, triple ou même quintuple. Nous verrons une étoile très connue qui à ce sujet est bien particulière !
Chaque étoile décrit une ellipse képlérienne, autour du centre de gravité du couple, qui est en un des foyers. Les excentricités de ces orbites sont égales.
Soient E1 et E2 les étoiles. Notons a1 et m1 le demi grand axe et la masse de E1, a2 et m2 ceux de E2. Alors, le centre de masse est tel que :
m1 a1 = m2 a2
Plus la masse de E1 est grande, plus petit sera son demi grand axe.
| Par exemple, si m1 = 10 m2 : |
Voici une animation montrant un couple d’étoiles de masses différentes (m2 = 2 m1, donc a1 = 2 a2), tournant autour de leur centre de gravité commun.
L’animation permet de faire varier l’inclinaison des orbites, de 90° (les orbites sont vues de dessus), à 0° (elles sont vues exactement par la tranche). On peut également modifier l’excentricité des orbites. Il serait facile de démontrer qu’une ligne imaginaire joignant à tout instant les deux étoiles, devrait passer par le foyer commun (croix jaune) des orbites. L’animation permet de tracer ou non cette ligne pour le vérifier.
Si maintenant on se place dans un référentiel tel que l’une des étoiles (la plus massive par exemple) est fixe, alors l’autre décrit autour d’elle une orbite képlérienne aussi, mais son demi grand axe est la somme des deux vrais :
a = a1 + a2
De plus, l’orbite n’est jamais vue dans les circonstances idéales de l’animation, mais en projection quelconque sur la ligne de visée.
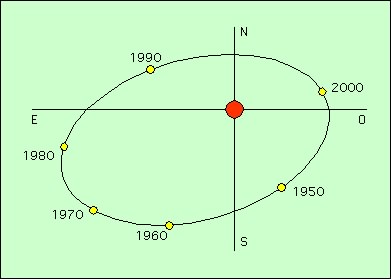
ξ Ursæ Majoris
ξ UMa est une étoile proche, dont les deux composantes sont visibles. Sur ce schéma, remarquez que son orbite apparente, vue depuis la Terre, est bien une ellipse, mais que l’étoile principale n’est pas au foyer de cette ellipse. Ceci est un effet de perspective, et la déformation est fonction de l’inclinaison des orbites par rapport à la Terre. Un calcul permet de reconstruire l’orbite exacte, et donc de déterminer le demi grand axe a du couple. Cet effet de projection ne se produit pas dans l’animation, parce que le grand axe des deux orbites est toujours perpendiculaire à la ligne de visée.
La valeur du demi grand axe de leur orbite, par rapport à la taille des étoiles, joue un rôle important dans les propriétés physiques. On parle de double lâche lorsque les composantes sont à des dizaines ou des centaines d’Unités Astronomiques (ce qui en fait déjà des étoiles très proches), et de couples serrés lorsque cette distance est inférieure à l’unité astronomique, tout en restant supérieure au rayon de l’étoile (sans quoi elles fusionnent).
Dans un couple très serré, il peut y avoir échange de matière entre les deux composantes, mais ceci est une autre histoire, que nous verrons en étudiant les étoiles variables.
Les doubles que nous allons étudier maintenant sont de vrais couples, mais dans lesquels une seule composante, la plus brillante, est observable. Dans le cas contraire, ce seraient des couples optiques ! Mais l’étoile la plus brillante est assez proche de la Terre pour qu’on puisse analyser son mouvement propre.
Toute étoile se déplace sur le fond du ciel, en ligne droite si on ne considère qu’un court intervalle de temps (quelques siècles...). Un couple n’échappe pas à la règle. Mais aucune des deux étoiles ne va suivre cette ligne idéale ; c’est le centre de masse qui la parcourra. Aussi, dans son mouvement elliptique autour du centre de masse, l’étoile principale va suivre une trajectoire ondulante, avec des boucles de part et d’autre de la trajectoire du centre de masse. Bien sûr, les deux boucles seront inégales, d’importance inversement proportionnelle aux masses des composantes.
L’analyse de la trajectoire de Sirius a permi, dès 1830, de montrer que cette étoile est double, bien qu’il ait été impossible de voir le compagnon. Par des mesures astrophysiques, on a pu évaluer la masse de Sirius A. Et de son chemin dans le ciel déduire la masse du compagnon, Sirius B. On a vu que cette masse était de l’ordre d’une masse solaire, mais avec une luminosité très faible, alors indétectable. Il s’agissait donc d’une étoile de masse normale, mais beaucoup moins lumineuse qu’une étoile standard (de la Séquence Principale). L’explication était que sa surface était très petite, donc aussi son rayon. Il s’agissait d’une toute petite étoile. C’est la première naine blanche détectée.
La méthode d’observation est ici la mesure de la quantité de lumière reçue, à l’aide d’une cellule photoélectrique autrefois, d’une camera CCD aujourd’hui. Lorsque la luminosité varie dans le temps de manière cyclique, avec des périodes où la lumière est constante, et deux minima, on en déduit qu’il s’agit d’une binaire.
Les doubles photométriques montrent le cas où une étoile passe devant l’autre, produisant des éclipses. La luminosité étant de ce fait variable, on nomme ces étoiles variables à éclipses. Nous les étudierons donc avec les autres variables.
Les doubles spectroscopiques sont des étoiles apparemment simples, et ne montrant pas de variations significatives de la luminosité (il n’y a pas d’éclipses). Mais lorsqu’on prend un spectre de leur lumière, on observe parfois un dédoublement des raies spectrales. Si ce dédoublement est permanent, et périodique, on l’explique par la présence de deux étoiles, dont la vitesse par rapport à la Terre est différente, impliquant un effet Doppler lui aussi différent. C’est un couple d’étoiles vue en perspective. La vitesse des deux étoiles varie périodiquement au cours du temps, et les raies spectrales aussi. Voyez l’animation explicative de ce phénomène.
Si l’inclinaison de l’orbite par rapport à la Terre est assez faible, les étoiles s’éclipsent mutuellement, et on peut les détecter aussi comme doubles photométriques. Alors, ce sont des étoiles variables. Aussi, nous verrons l’explication des doubles spectroscopiques en étudiant les étoiles variables (l’animation indiquée ci-dessus explique également ce cas).
Les étoiles doubles présentent un intérêt capital en astrophysique. Comment déterminer la masse d’une étoile ? Certainement pas en observant sa lumière. En fait, il n’existe qu’une seule façon directe de le faire : déterminer son influence gravitationnelle sur un objet en orbite autour. C’est de cette façon qu’on a mesuré les masses des planètes, en observant le ballet de leurs satellites. La loi de la Gravitation Universelle de Newton permet de calculer la masse en fonction des paramètres de l’orbite.
Toute la physique des étoiles est basée sur la connaissance de leur masse (théorème de Vogt-Russel), et celle-ci est le paramètre le plus important, qui détermine leur évolution. Heureusement, il y a suffisamment d’étoiles doubles de tous les types spectraux proches de la Terre, qui permettent de connaître les masses des étoiles de tous types. A partir de là, l’étude des étoiles a pu se faire.
Considérons un couple orbital dont on puisse mesurer la période T, ainsi que les deux demi grands-axes apparents a1 et a2 (voir plus haut). Nous avons déjà les deux équations :
| a = a1 + a2 | et | m1 a1 = m2 a2 |
a1 et a2 étant connus (mesurés sur le ciel), on calcule a et le rapport m1 / m2 = a2 / a1 ; désignons par r ce rapport r = m1 / m2, qui est donc mesuré.
Les deux objets suivent les lois de Kepler, et en particulier la troisième qui lie le demi grand-axe et la période :
a3 / T2 = m1 + m2
a et T étant connus, on en déduit la somme des masses m1 + m2 ; désignons par s cette somme s = m1 + m2
On connait donc, maintenant, la somme et le rapport des masses :
r = m1 / m2 => m1 = r m2
Reportons cette valeur de m1 dans l’expression de la somme :
s = r m2 + m2 = m2 (r + 1)
d’où :
m2 = s / (r + 1)
m2 est maintenant connue ; on reporte sa valeur dans l’expression de la somme et on en tire m1 :
m1 = s - m2
Donc, s et r étant mesurés :
m2 = s / (r + 1) m1 = s - m2 |
Ainsi, la mesure de T, a1 et a2 permet de calculer les masses des deux composantes du couple. Analysant par ailleurs leur lumière, on détermine leur type spectral. Ceci permet d’étudier le type spectral, c’est-à-dire le fonctionnement de l’étoile, en fonction de sa masse. C’est par là qu’on a pu déterminer une relation fondamentale entre la masse d’une étoile et sa luminosité, et fonder toute l’astrophysique stellaire.
Quelques mots à propos des systèmes comprenant plus de deux étoiles.
On y distingue assez souvent une structure hiérarchique, en ce sens qu’un système triple est souvent composé d’un couple dont le centre de masse est lui-même en orbite avec une troisième étoile. On trouve aussi deux couples, chacun jouant le même rôle qu’une étoile simple dans une association par 4.
Un système multiple qui ne présenterait pas ce genre de particularité serait dynamiquement instable, et se dissocierait très rapidement après sa formation.
La nature nous offre quelques beaux exemples. Ainsi, une étoile très connue de la Grande Ourse, Mizar, forme une double visuelle avec Alcor. Alcor est connue depuis l’Antiquité, mais il est probable que sa magnitude a diminué (sa luminosité a augmenté). Le nom Alcor vient de l’arabe, et évoque la difficulté. Cette petite étoile était donc un test de bonne vue, alors qu’aujourd’hui elle est facilement visible. Il s’agit d’un couple optique, les deux étoiles n’étant pas liées gravitationnellement : Mizar est à 78 AL de nous, Alcor se situe 3 AL plus loin.
Mais une observation télescopique d’amateur montre vite que Mizar est double. C’est même la première double télescopique connue, car elle a sans doute été vue par Galilée en 1620, et elle est mentionnée par Riccioli en 1650. Mieux, c’est la première double mesurée par photographie, par Georges Bond en 1857.
Enfin, une observation spectroscopique de chacune des deux composantes nous révèle qu’elles sont toutes deux des doubles spectroscopiques !
Autre exemple magnifique : Albireo, dans le Cygne (c’est l’étoile qui forme le bec du cygne). Albireo est un vrai couple orbital exceptionnel dans un petit télescope : la première composante, A, est jaune orangée, la seconde, B, est bleu-vert. Les magnitudes sont assez proches (3,1 pour A, 5,1 pour B), et le contraste de couleur fait toute la beauté de ce couple bien connu des amateurs. L’écartement des deux étoiles est de 34,3" ce qui en fait un couple facile. Sa période est supérieure à 75.000 ans, mais elle est mal déterminée. La distance de ce système est de 385 AL.
A est de type spectral K3II ; sa classe de luminosité II la place parmi les supergéantes ; son type K3 lui confère une température superficielle de 4.100 K. La magnitude et la température superficielle permettent de calculer son diamètre, qui est de l’ordre de 20 fois celui du Soleil. Mais A est de plus une binaire spectroscopique.
B, la composante bleu-vert, est de type B8V ; c’est une naine de la Séquence Principale (classe V) ; le type B8 en fait une étoile massive et chaude : 12.000 K ; son diamètre est 3 fois celui du Soleil. Cette étoile est en rotation très rapide, et la force centrifuge à l’équateur lui fait perdre de la masse. L’étoile est maintenant entourée d’un disque de matière provenant de cette perte.
---=OO=---