Historique de Marseille
| liens |
le 02/01/25
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 02/01/25 |
||||
| �� Cosmologie | |||||||
… Ou, penchés à l’avant des blanches caravelles,
Ils regardaient monter en un ciel ignoré
Du fond de l’océan des étoiles nouvelles.
José Maria de Heredia, Les conquérants
Table des matières
1.1 Cosmologies antiques
1.2 Le cadre de la Cosmologie
2 Bases observationnelles
2.1 Répartition de la matière visible
2.2 Densité moyenne de l’Univers
2.3 Matière sombre
2.4 Matière noire
2.5 Expansion
2.6 Découverte théorique de l’expansion
2.7 Age de l’Univers
2.8 Temps caractéristique
3 Le Big Bang
3.1 Fond diffus cosmologique
3.2 Origine du fond cosmologique
3.3 Composition chimique de l’Univers
3.4 Energie noire
3.5 Composition de l’Univers
3.6 Les trois piliers
4 Bases théoriques
4.1 Réactions d’équilibre
4.2 Principe cosmologique
4.3 Horizon cosmologique
4.4 Problème de l’horizon
4.5 But de la cosmologie
4.6 Temps cosmique
5 Mise en équation du problème
5.1 Coordonnées comobiles
5.2 L’équation de Friedmann
5.3 Interprétation
5.4 Equation du fluide
5.5 Equation d’état
5.6 Equations du problème
5.7 Autre présentation de l’équation de Friedmann
5.8 Densité critique
5.9 Importance de la densité critique
6 Modèles
6.1 Univers de matière
6.2 Univers de rayonnement
6.3 Mélange
6.4 Univers vide
6.5 Utilité de l’inflation
6.6 Equation des omégas
7 Une histoire thermique de l’Univers
7.1 Le modèle de Big Bang de base
7.2 Le tout début : ère de Planck
7.3 Transition de phase Grande Unification
7.4 Ere des quarks : plasma quarks-gluons
7.5 Découplage des neutrinos
7.6 Formation des baryons (baryogénèse)
7.7 Annihilation des protons
7.8 Annihilation des électrons
7.9 Nucléosynthèse
8 Transition rayonnement-matière
8.1 Recombinaison
8.2 Découplage et Surface de dernière diffusion
8.3 Formation des structures
8.4 Ages sombres
8.5 Réionisation
9 Au-delà du modèle de base
9.1 Propriétés de la matière noire
9.2 Accélération
9.3 Quelques problèmes du modèle de base
10 L’inflation
10.1 Epoque de l’inflation
10.2 Taille de l’Univers observable
Jusqu’à une époque récente, l’Homme a toujours eu la préoccupation de comprendre son environnement dans son ensemble, sans en avoir les moyens. Sur le plan observationnel, l’œil nu est limité à quelques centaines d’années-lumière, c’est-à-dire à la proche banlieue du Soleil (à peine un dix-millionième de l’Univers observable en distance ; l’Univers observable est l’ensemble de ce que l’on peut voir aujourd’hui, il est défini plus loin. En volume, ce n’est plus que la fraction 10-21 de ce qui existe…). Les télescopes performants n’ont été construits qu’à partir de la seconde moitié du XIXe siècle, et l’observation du ciel très profond ne date que de quelques années.
La cosmologie a considérablement évolué avec le temps, et avec les découvertes que les nouveaux instruments permettaient à mesure de leur invention. Elle a donc commencé par une très longue période d’observation à l’œil nu, qui ne donnait accès qu’aux seuls astres directement visibles, les autres restant inconnus.
L’invention de la lunette, puis du télescope, ont ouvert le champ des étoiles d’abord, puis des nébuleuses et des galaxies. Mais la découverte de nouveaux objets n’était pas suffisante pour en comprendre l’organisation. Il fallait en plus un cadre théorique, qui permette de les expliquer, ainsi que leurs relations. Kepler a défini les premières lois du mouvement, ouvrant la voie à Isaac Newton qui a créé ce premier cadre, avec la Gravitation Universelle. Il a permi d’expliquer avec une grande précision les mouvements des planètes (à l’exception d’un petit résidu inexplicable, l’avance du périhélie de Mercure), et de représenter correctement le Système Solaire. Mais les connaissances de notre environnement ne permettaient guère d’aller plus loin.
Les nébuleuses, connues depuis longtemps, étaient ainsi nommées à cause de leur aspect télescopique. On les séparait en deux classes : les spirales et les autres. La question était ouverte de savoir si ces spirales étaient proches ou lointaines, mais les outils manquaient pour le déterminer. Proches, elles auraient été constituées de gaz ; lointaines, elles auraient été de grands rassemblements d’étoiles. Dans le premier cas, l’Univers restait limité à l’ensemble des étoiles que l’on connaissait. Mais dans le second cas, notre Voie Lactée devenait un rassemblement semblable aux nébuleuses spirales, et du coup l’Univers n’était plus limité à notre banlieue, mais explosait littéralement dans notre conception. La preuve instrumentale de cette seconde vision n’est venue qu’au début du XXe siècle grâce au télescope Hooker de 2,5 m.
A la même époque, en 1915, Albert Einstein publiait la Relativité Générale, théorie de la gravitation applicable à de grandes masses et de grandes vitesses. Ainsi, les observations et le cadre théorique nécessaire à leur interprétation sont contemporains.
Dès la publication de cette théorie, des chercheurs l’ont appliquée à l’étude de l’Univers : de Sitter (1917) a modélisé un Univers vide de matière, ne contenant que de l’énergie ; Alexandre Friedmann (29 juin 1922) et Georges Lemaître (1927) ont résolu le problème dans un Univers de densité uniforme, et montré qu’il devait être soit en contraction, soit en expansion.
Einstein de son côté, recherchait une solution stationnaire, n’envisageant pas que l’Univers puisse être différent aujourd’hui de ce qu’il était dans le passé. Pour cette raison, n’obtenant pas de solution satisfaisante à ses yeux, il a légèrement modifié son équation (ajout de la constante cosmologique), pour y parvenir. Mais il a été démontré plus tard que l’équilibre obtenu est un équilibre instable, ce qui signifie que toute perturbation ne peut que s’amplifier, produisant la contraction ou l’expansion. A cette nouvelle, Einstein a amèrement regretté d’avoir fait cet ajout.
La Relativité Générale reste le seul cadre, actuellement, qui permette de représenter l’Univers dans son entier ; c’est la clé de la Cosmologie. On peut donc dire qu’il y a deux époques pour la Cosmologie : avant et après la Relativité Générale.
Au début de XXe siècle encore, Harlow Shapley et Vesto Slipher (1915) découvraient que toutes les galaxies (les nébuleuses spirales) dont ils prenaient les spectres, présentaient un décalage de leurs raies spectrales vers le rouge. L’explication la plus vraisemblable a vite été donnée : l’Univers est en expansion, et les distances entre les galaxies s’accroissent parce que l’Univers grossit. Cette interprétation n’est pas immédiate, mais nécessite un modèle théorique, fourni justement par la Relativité Générale. Sur le plan théorique, la Gravitation Universelle de Newton permettait d’aborder le problème, mais elle n’était conçue que dans un contexte de faibles masses et posait des problèmes sérieux qui en limitaient l’application en Cosmologie.
Georges Lemaître a déduit les conséquences passées de l’expansion : en regardant le film à l’envers, on voit l’Univers se contracter jusqu’à une densité très grande. Il en a déduit que l’Univers avait dû se trouver dans un état d’extrême condensation. En vertu des idées de l’époque sur la radioactivité, il a nommé cet état atome primitif. Cette notion n’est autre que le Big Bang, sauf le nom. L’essentiel est l’existence d’un instant initial.
La Relativité Générale est-elle la théorie ultime pour décrire l’Univers ? N’oublions pas qu’elle ne décrit que la gravitation ! Dans l’Univers actuel, très dilué et froid, la gravitation est largement prépondérante. Mais en remontant le temps à l’envers de l’expansion, on arrive à un instant où la matière était si dense et chaude, constituant un milieu de particules élémentaires dans lequel la gravitation devient aussi intense que les autres interactions, et ne peut plus être négliglée. Toutes les interactions doivent être prises en compte par une seule théorie globale, qui unifie la Relativité Générale, pour la gravitation, avec la Mécanique Quantique, qui traduit les autres interactions.
La Relativité Générale utilise, pour la gravitation, un cadre spatio-temporel continu mais déformable. Elle se base sur l’équivalence entre la structure de l’espace-temps et son contenu matière-énergie. Or la Mécanique Quantique indique que l’énergie est quantifiée (ne s’échange que par valeurs discrètes). Mélanger les deux théories reviendrait donc à quantifier la structure même de l’espace-temps, d’où la notion parfois évoquée d’une structure microscopique spongieuse de l’espace-temps.
Il y a bien longtemps que les physiciens cherchent à quantifier la gravitation, mais pour l’instant sans succès. Dans ces conditions, la Relativité Générale reste la théorie pertinente pour décrire l’Univers, dans la limite où la gravité est prépondérante, c’est-à-dire après ce qu’on appelle le mur de Planck. Entre le mur de Planck et le Big Bang, la Relativité ne peut tout simplement rien dire, et en particulier ne peut pas valider la notion même de Big Bang.
Aujourd’hui, la fameuse constante cosmologique est vue sous un angle bien différent, avec une autre interprétation : peut-être fera-t-elle un retour utile dans la théorie, c’est au moins ce que certains pensent maintenant. Si elle est positive, elle produit une expansion de l’Univers, qui s’accorde bien avec des observations récentes (accélération de l’expansion).
La théorie cosmologique qui explique au mieux les faits d’observation est donc bien le célèbre Big Bang, sans considérer l’époque avant le mur de Planck. Mais les choses ne sont pas aussi simples que le schéma de base, qui présente bien des inconvénients. Dans le principe de cette théorie, il existe un instant zéro, à partir duquel les choses commencent à exister. Une description complète des diverses phases par lesquelles est passé l’Univers est donnée, et prévoit ce que l’on devrait observer. La force de la théorie tient justement dans certaines observations qui confortent cette vision. Mais l’existence même de cet instant zéro n’est pas sans poser des problèmes difficiles, et il est peut-être tout simplement inutile. On peut envisager que, autour de cet instant théorique, la physique soit assez différente de ce que nous connaissons, et que l’instant zéro n’existe pas. Notons de plus que l’existence d’un instant zéro entraîne celle d’un âge de l’Univers.
Nous présenterons d’abord certaines cosmologies antiques, adaptées aux observations à l’œil nu. Elles ont beaucoup d’intérêt sur le plan philosophique, car elles nous indiquent comment les Hommes qui les ont conçues se représentaient le Monde qui les entourait. Aujourd’hui, nous sommes dans une situation tout à fait semblable : nous nous représentons le monde (l’Univers) en fonction de nos connaissances observationnelles et de nos outils théoriques d’interprétation. L’avenir dira dans quelle mesure nos idées actuelles sont en adéquation avec la réalité.
Cosmologie avant 1915
Cosmologie après 1915
Depuis 1915, la Relativité Générale permet, grâce aux relations qu’elle établit entre les propriétés de l’univers et son contenu, de parler scientifiquement de sa description. Mais aussi, d’envisager une évolution de l’univers, bien qu’Einstein ait voulu qu’il soit statique pour des raisons philosophiques…
C’est donc dans ce cadre, seul disponible actuellement, que s’est développée la Cosmologie. La Relativité Générale étant une théorie incomplète (qui ne décrit que la gravité), elle ne peut être la description ultime de l’univers (si ceci a un sens). Mais elle ne rencontre que des succès dans son application locale (toutes les propriétés qu’elle prévoit ont été vérifiées à ce jour). Il est donc tout à fait pertinent de l’utiliser pour la cosmologie.
Avant de penser à établir une théorie, il faut savoir de quoi on va parler exactement, c’est-à-dire faire l’inventaire de l’Univers tel qu’il nous apparaît aujourd’hui.
Le point de départ est l’état actuel de l’Univers, tel qu’il ressort des multiples observations que l’on fait depuis presque un siècle. Les ingrédients sont :
En s’éloignant de la Terre, nous observons successivement :
Les descriptions ci-dessus montrent bien la difficulté de déterminer la masse volumique de l’Univers. Localement (ce terme englobant des distances jusqu’à la centaine de méga-parsecs), la masse est très inégalement répartie, les inhomogénéités sont énormes : les étoiles sont des condensations de matière à forte densité (quelques g cm-3 en moyenne), au milieu de grands espaces vides. Le système solaire est constitué du Soleil, de grande masse volumique, entouré de vide. La masse volumique moyenne résulte de la combinaison de ces deux valeurs. Aux échelles supérieures, le phénomène de concentration-vide s’accentue encore. Ce n’est qu’en atteignant des distances de quelques centaines de méga-parsecs que l’on distingue l’homogénéité. Mais de notre petit observatoire terrestre, c’est bien difficile à sonder.
La quantité de matière présente dans l’Univers actuel est décrite par la masse volumique moyenne de l’Univers. En faisant la moyenne, on divise la masse totale par le volume total, ignorant la répartition de la matière dans ce volume.
Donc, la masse volumique moyenne de l’Univers nous renseignera sur ses propriétés à très grande échelle (plusieurs centaines de méga-parsecs, où l’Univers est homogène), mais pas sur ses propriétés locales. Celles-ci seront tout simplement oubliées. Cette simplification est indispensable pour pouvoir aborder le problème, qui sinon serait bien trop complexe.
Pratiquement, les mesures de cette masse volumique sont très difficiles à faire, car elles nécessitent l’évaluation précise de la quantité de matière qui emplit un certain cube d’Univers. Or un tel cube contient des galaxies, que l’on détecte par la lumière qu’elles nous envoient, mais qu’on ne peut pas peser ! On peut cependant évaluer la masse des étoiles qui produisent cette lumière. Pour cela, il faut compter les étoiles, et déterminer leurs propriétés moyennes.
L’étude des étoiles proches montre que leur masse moyenne est proportionnelle à leur luminosité moyenne, pour un grand nombre d’étoiles de types divers :
M = 4 L
où la masse M est donnée en masses solaires M, et la luminosité L en luminosités solaires L. Mesurant la luminosité totale d’une galaxie, on en déduit donc sa masse. C’est ainsi qu’on obtient la masse globale d’une galaxie, masse lumineuse s’entend.
La luminosité globale d’une galaxie est évaluée à Lgal ≃ 2 1010 L. D’ou sa masse :
Mvis ∝ 4 Lgal = 4 × 2 1010 M = 8 1010 M
Il reste à déterminer le nombre de galaxies dans un volume donné, c’est-à-dire à les compter, tout simplement. On trouve un nombre moyen de ngal ≃ 0,005 Mpc-3. Ayant la masse d’une galaxie, et le nombre de galaxies par unité de volume, la densité en découle immédiatement :
ρvis ∝ Mvis ngal = 8 1010 M × 0,005 Mpc-3 = 4 108 M Mpc-3
Cette densité, ramenée à des unités plus habituelles, est du même ordre que celle donnée plus haut. Elle signifie que chaque cube d’Univers de 1 Mpc de côté contient une masse moyenne de 4 108 M, soit l’équivalent de 400 millions de fois le Soleil.
La masse du Soleil est de 1,988 1030 kg, 1 Mpc = 3,086 1022 m. La densité est donc :
⟨ρvis⟩ = 4 108 M Mpc-3 = 4 108 × 1,988 1030 kg × (3,086 1022 m)-3.
Soit : ⟨ρvis⟩ = 7,952 1038 / 29,389 1066 kg m-3 = 0,27 10-28 kg m-3 = 2,7 10-30 g cm-3. On retrouve le même ordre de grandeur que ce qui était indiqué plus haut.
En surmontant pour le mieux toutes ces difficultés, on évalue à peu près correctement la masse volumique actuelle de l’Univers, et la valeur obtenue est très faible :
ρ = 10-26 kg m-3 = 10-29 g cm-3
La masse du proton étant de 1,67 10-27 kg, elle correspond à peu près à 6 atomes d’hydrogène par m3.
Malheureusement (pour la mesure précédente), les galaxies contiennent aussi de la matière obscure : du gaz qui n’est pas dans les conditions physiques qui lui permettraient de rayonner (par exemple les nébuleuses sombres, tels les objets de Barnard mais aussi les régions HI qui rayonnent à 21cm). La matière visible n’est que la partie émergée de l’iceberg…
C’est la première source d’incertitude, car la matière sombre n’est pas prise en compte dans l’évaluation précédente. Par analogie avec notre Galaxie, où l’on peut faire des observations fines, et avec les galaxies proches, également accessibles, cette matière est évaluée à quelques 10 fois la matière visible, ce qui est considérable.
Mais le plus grave pour la mesure, se présente lorsqu’on étudie la dynamique : les nuages d’hydrogène qui entourent la Galaxie devraient tourner comme les planètes autour du Soleil, c’est-à-dire d’autant plus lentement qu’ils sont plus éloignés, puisque toute la masse attirante se trouve en-dessous. Or on sait depuis les travaux de Fritz Zwicky (1930) que ce n’est pas le cas, et qu’ils tournent tous à la même vitesse, quel que soit leur éloignement du centre. Pour expliquer les mouvements de ces nuages, il faudrait que la Galaxie ait une masse 10 fois supérieure !
Dans les amas aussi, les galaxies se déplacent bien trop vite pour que l’amas soit stable. En ne considérant que la masse visible des étoiles, ils devraient se disloquer dans l’espace en très peu de temps, ce qui fait qu’on ne devrait observer que quelques rares amas, aléatoirement formés depuis peu et pas encore disloqués. Mais on en observe beaucoup, donc ils sont stables sur des durées comparables à l’âge de l’Univers, donc il y a de la masse invisible pour expliquer cette stabilité. Le déficit est ici de 400 fois la masse visible !
Ces observations sont à la base de l’idée de matière noire : il faut bien expliquer les observations. On invoque pour cela, une matière qui agit gravitationnellement comme la matière ordinaire, mais qui est insensible à l’interaction électromagnétique (puisqu’elle n’émet pas de lumière, et n’en absorbe pas, sans quoi on la verrait). Sans cette matière hypothétique, les parties externes des galaxies seraient éjectées par la force centrifuge (ou plus correctement, par leur inertie) ; il en serait de même des galaxies dans les amas. Pour l’instant, cette matière noire ne se manifeste que par ce biais.
De 1919 à 1922, dans le but de mesurer leurs vitesses, Vesto Slipher a mesuré le décalage spectral des galaxies proches et découvert qu’elle s’éloignaient toutes (presque), indiquant que l’Univers était en expansion. En 1924, Henrietta Leavitt a montré comment mesurer les distances dans l’Univers proche, grâce à la relation qu’elle a déterminée entre la période et la luminosité des céphéides. A la suite de cela, Lundmark a obtenu en 1925 une corrélation entre la vitesse radiale des galaxies et leur distance. La dépendance qu’il en déduisait était quadratique, ce qui traduit la difficulté induite par les mouvements propres des galaxies proches. En 1927, Humason commence un programme de mesure des décalages spectraux de galaxies faibles, donc plus lointaines. Cette même année, Georges Lemaître publie sa théorie de l’atome primitif, qui est le premier modèle expliquant l’Univers en expansion, et qui est la base du Big Bang. Deux ans plus tard, en 1929, Hubble publie un article dans lequel il suggère une relation linéaire (conforme à la prédiction de Lemaître), entre le décalage spectral et la distance de galaxies proches. Cette relation ne s’appuyait que sur des galaxies dont les mouvements propres sont importants (car elles sont toutes plus proches que l’amas de Virgo), et la dispersion des vitesses ne donnait qu’une grossière augmentation de la vitesse avec la distance (cf Jean-Pierre Luminet, L’invention du Big Bang). Elle a malgré tout été nommée loi de Hubble.
Le décalage spectral est le déplacement des raies d’absorption (ou d’émission) observé dans le spectre d’un objet, par rapport à un spectre pris au laboratoire (c’est-à-dire au repos). Le décalage spectral mesure la vitesse d’un objet par rapport à l’observateur. Il est défini comme la différence relative entre la longueur d’onde mesurée λ0 et la longueur d’onde émise λ :
![]()
Considérons un objet à z = 1. On a alors 1 = (λ0 - λ) / λ ⇒ λ0 = 2 × λ
Toutes les longueurs d’onde de cet objet sont doublées. Par exemple, un rayonnement émis à la limite de l’ultra-violet (0,4 µm), se retrouve à la limite de l’infra-rouge (0,8 µm). Le décalage atteint la largeur totale du spectre visible !
La solution qui convenait était donc l’expansion. Mais Hubble a indiqué que les galaxies proches nous fuient à une vitesse qui est proportionnelle à leur distance, et expliqué le décalage vers le rouge par un effet Doppler dû à une vitesse d’éloignement réelle. Or l’expansion ne produit pas un véritable effet Doppler, puisque les galaxies ne s’éloignent pas de nous et sont immobiles dans l’espace en expansion qui se dilate. De plus, envisager que toutes les galaxies s’éloignent de nous reviendrait à nous placer au centre de l’Univers… ce à quoi on a renoncé depuis Copernic !
Les galaxies ne s’éloignent pas de nous, c’est bien l’espace qui nous en sépare qui est en expansion. Et cette propriété avait été également trouvée théoriquement par Alexandre Friedmann quelques années plus tôt, à partir de l’équation d’Einstein. Friedmann a publié exactement la loi de proportionnalité deux ans avant Hubble (on peut voir à ce sujet le livre de Jean-Pierre Luminet l’invention du Big Bang).
La vitesse trouvée par Hubble était aussi bien trop grande, de l’ordre de dix fois. La constante qui représente cette vitesse aujourd’hui (car la constante est en fait variable…), est appelée constante de Hubble, et notée H0. L’indice 0 signifie aujourd’hui. La valeur qu’on lui reconnaît actuellement, déduite de mesures récentes, est de :
| H0 = 72 ± 8 km s-1 Mpc-1 | HST 2001 | |
| H0 = 71,9 ± 2,6 km s-1 Mpc-1 | WMAP 2008 |
Remarquez l’incertitude sur la mesure : 8 km s-1, par rapport à 72 km s-1, représente 11 %. En 2008, l’erreur tombe à un peu moins de 4 %. Des mesures nouvelles seront encore nécessaires pour arriver à une valeur vraiment digne de confiance. Elle signifie qu’à chaque seconde, l’Univers s’accroît dans toutes les directions de 72 km pour chaque mégaparsec de distance. Cette valeur donne le vertige, parce que 72 km de plus à chaque seconde semble énorme ! Mais cet accroissement correspond à un million de parsecs, ce qui est une distance assez impressionante aussi. On se propose de traduire cette valeur dans des unités qui nous sont plus sensibles que le mégaparsec :
H0 = 7,4 µm siècle-1 km-1
Ceci signifie que chaque kilomètre d’Univers s’allonge de 7,4 µm en un siècle ! C’est la longueur d’une grosse bactérie… Vu sous cet angle, l’expansion semble bien plus raisonnable. Mais lorsqu’on considère des milliards d’années-lumière (ou de parsecs), les choses ont une autre dimension.
Il faut aussi comprendre que pour les courtes distances (inférieures au méga-parsec), l’expansion ne se fait pas sentir : les autres forces de la Nature sont bien trop importantes pour que la matière puisse se plier à l’expansion générale. Ainsi, les galaxies sont fortement liées gravitationnellement, et ne subissent donc pas la dilatation de l’espace. Ce n’est qu’à l’échelle des distances entre les amas de galaxies que l’expansion se fait sentir, et prend toute son ampleur. D’autre part, les objets qui nous entourent (y compris nous-même), sont gouvernés par les forces électromagnétiques qui définissent les distances entre les atomes. Tout ceci est donc insensible à l’expansion.
Un autre point peut sembler délicat. Si on applique la loi de Hubble à des galaxies très éloignées, on peut trouver une vitesse supérieure à la vitesse de la lumière ! Il suffit de considérer une galaxie située à une distance d telle que c = H d, soit d = c / H. Avec H = 72 km s-1 Mpc-1, on trouve d = 300.000 km s-1 / 72 km s-1 Mpc-1 = 4.166 Mpc. Soit 4 milliards de parsecs ou 13 milliards d’années-lumière. C’est à peu près la taille de l’Univers observable. Une galaxie plus éloignée semblerait s’éloigner à une vitesse supérieure à celle de la lumière, mais ceci ne pose pas de problème, car il ne s’agit nullement d’une vitesse des galaxies l’une par rapport à l’autre, mais d’un effet dû à l’expansion de l’Univers : c’est l’espace qui s’étend entre les deux galaxies, qui chacune est immobile dans son espace. Il ne s’agit donc absolument pas d’une vitesse relative réelle des deux galaxies, et la Relativité n’est pas mise en défaut.
L’expansion de l’Univers a été découverte par Georges Lemaître, en résolvant l’équation de Friedmann, elle-même tirée de l’équation d’Einstein qui décrit la géométrie de l’espace-temps. Alexandre Friedmann a aussi obtenu un résultat semblable. Alors qu’Einstein lui-même cherchait une solution stationnaire (Univers en équilibre), ce qui l’a amené à introduire la constante cosmologique, Lemaître a démontré que les seules solutions possibles représentaient un Univers soit en expansion, soit en contraction. Théoriquement, il est impossible de choisir entre les deux, mais il était clair qu’il fallait s’attendre à un Univers non statique.
Lemaître avait connaissance des travaux de Vesto Slipher, qui montrait que les galaxies avaient toutes (presque) un décalage vers le rouge et non vers le bleu. Il en a déduit que l’univers était en expansion.
Il est facile de montrer que, dans un univers homogène, la vitesse de deux galaxies l’une par rapport à l’autre, est proportionnelle à la distance qui les sépare.

A l’instant t0, les galaxies B et C se trouvent à la distance a et 2a respectivement de A. Plus tard, à l’instant t1, elles se trouvent respectivement aux distances 2a et 4a (l’homogénéité implique que les distances AB et BC ont été multipliées par une même valeur, sinon les propriétés de l’espace-temps ne seraient pas les mêmes en des points différents). Entre ces deux instants, l’augmentation de distance à A de B est de ΔdB = 2a - a = a, celle de C est de ΔdC = 4a - 2a = 2a. Donc, la vitesse d’éloignement de B est vB = ΔdB / Δt = a / Δt, et celle de C est vC = ΔdC / Δt = 2a / Δt. Donc vu de A, la vitesse d’éloignement de C est double de celle de B. On pourrait prendre des points à des distances plus grandes, le résultat serait de même nature. On en déduit :
v = H d
où H est une constante. La vitesse d’éloignement est proportionnelle à la distance de l’objet considéré.
Cette relation est connue sous le nom de loi de Hubble, parce que ce dernier a trouvé, quelques années plus tard, que quelques galaxies proches présentaient une vitesse d’éloignement grossièrement proportionnelle à leur distance.
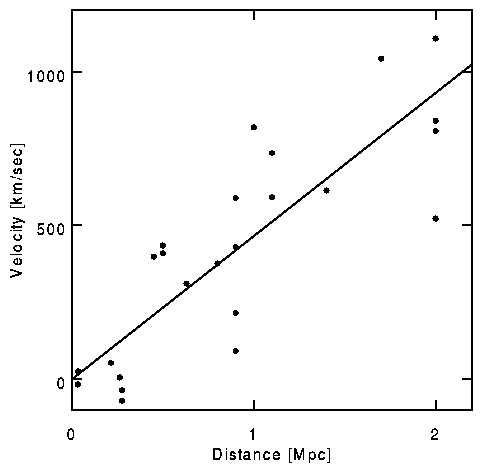
On voit la très forte dispersion, due aux mouvements propres des galaxies observées, qui sont du même ordre de grandeur que l’expansion. L’échantillon utilisé n’est pas représentatif, ne comprenant que des galaxies plus proches que l’amas de Coma.
On en tire facilement d = v / H qu’on écrit sous la forme d = v × 1 / H. Or, pour obtenir une distance, il faut multiplier une vitesse par un temps. Donc, 1 / H est un temps. On pose :
t = 1 / H
D’où d = v t. Comment interpréter ce temps ? d est la distance qui nous sépare d’une galaxie G donnée. En considérant que l’expansion dure depuis que les galaxies étaient toutes regroupées (distance nulle, début de l’Univers), et sachant que G se déplace à la vitesse apparente v (supposée constante), elle a mis le temps t = 1 / H pour arriver à sa position actuelle. Donc, ce temps est l’âge de l’Univers (temps écoulé entre le rassemblement des galaxies et aujourd’hui).
Un autre raisonnement se base sur les unités : H = 72 km s-1 Mpc-1 = (72 km s-1) / Mpc. C’est une vitesse divisée par une distance. Et une vitesse divisée par une distance est un temps !
Attention : dans ce raisonnement, on a supposé H constante dans le temps. Or ceci n’est qu’une approximation. En effet, l’expansion de l’Univers est ralentie par l’attraction gravitationnelle que les amas de galaxies exercent les uns sur les autres. Donc, l’expansion a dû être plus rapide dans les débuts de l’Univers. Dans ce cas, le temps est plus petit, et donc l’Univers moins vieux que 1 / H. Mais en plus, on a montré récemment que l’expansion s’accélère, depuis un milliard d’années à peu près, ce qui complique encore un peu l’interprétation.En résumé, la valeur 1 / H0 (valeur de H aujourd’hui) est un ordre de grandeur de l’âge de l’Univers, qui doit être modulé par le fait que H n’est pas constante dans le temps. L’âge fini de l’Univers, borné par 15 Ga, est attesté par le fait qu’on ne trouve ni objets astronomiques, ni radionucléides plus vieux.
A un instant quelconque dans l’histoire de l’Univers, la valeur t = 1 / H représente toujours un temps. C’est le temps écoulé depuis le Big Bang. Mais ce temps est lié à la vitesse d’expansion, qui n’a pas de raison a priori d’être constante. Donc, à tout instant, 1 / H représente le temps caractéristique d’expansion, le temps pendant lequel les dimensions de l’Univers changent significativement. En un temps plus bref, on peut considérer que les propriétés de l’Univers ne changent pas beaucoup.
Il sera intéressant de comparer ce temps caractéristique avec le temps propre de certains phénomènes physiques. Si un phénomène nécessite un temps supérieur au temps caractéristique d’expansion pour se réaliser, les conditions physiques auront changé avant qu’il ait pu se produire de manière significative. Ainsi, il y aura une course entre l’expansion et les phénomènes qui peuvent se dérouler dans certaines conditions, forcément éphémères. Nous verrons ce mécanisme à l’œuvre plusieurs fois.
Si l’Univers a toujours été en expansion, ce que rien ne vient contredire, il a eu un début, instant 0, point de départ de l’expansion. On le situe vers 13,7 milliards d’années, à 200 millions d’années près. La densité et la température de l’Univers ont été infinies à cet instant origine (si rien ne s’oppose à l’extrapolation jusqu’au temps t = 0).
L’existence de ce début nous autorise à parler de l’âge de l’Univers, en comptant le temps écoulé depuis.
Mais nous pourrons aussi écrire l’histoire de l’Univers. A gros traits, la densité et la température de l’Univers ne feront que décroître au cours du temps, produisant des changements de conditions physiques extrêmement importants. Au début, le milieu était à une température que l’on ne peut pas produire en laboratoire, et la physique qui le décrit est donc inconnue. Il ne nous sera donc pas possible d’écrire l’histoire de l’Univers jusqu’à l’instant 0, jusqu’au Big Bang lui-même. Les tout premiers instants resteront encore dans l’ombre.
Mais ensuite, lorsque l’Univers s’est suffisamment refroidi, les conditions physiques deviennent accessibles à nos connaissances, et ce que nous pourrons en dire prend sons sens. L’expansion était si rapide au début, que la température a baissé très brutalement. Notre compréhension de l’Univers commence donc un très bref instant après le Big Bang.
Disons tout de suite que le Big Bang est une notion théorique. En effet, puisque la physique qui le concerne nous est inconnue, nous ne pouvons savoir s’il a eu lieu réellement, ou si des phénomènes que nous ignorons l’auront empêché. On peut se poser des questions sur la signification d’une densité infinie… Mais se poser des questions à son sujet ne constitue par une preuve de non existence !
Dans la suite, nous considérerons donc que quelque chose a eu lieu, qui a amené l’Univers dans des conditions de densité et de température très élevées. Et nous tenterons de raconter l’histoire de l’Univers à partir de là.
Le fond micro-onde (fond diffus cosmologique, Cosmic Microwave Background, CMB), découvert accidentellement par Penzias et Wilson en 1965 (prix Nobel 1978 pour cette découverte), est aujourd’hui bien connu. En particulier, sa température moyenne (très proche de la température effective) est précisément de 2,725 K.
Il présente les caractéristiques suivantes :
La première analyse précise a été faite par le satellite COBE (COsmic Background Explorer) de la NASA, pour une couverture totale du ciel. Mais il a été observé avec plus de précision sur une portion limitée par le ballon européen BOOMERANG. A ces instruments pionniers a succédé le satellite WMAP (Wilkinson Microwave Anisotropy Probe), qui a précisé les résultats. Enfin, le satellite européen Planck a donné un niveau de précision supplémentaire.
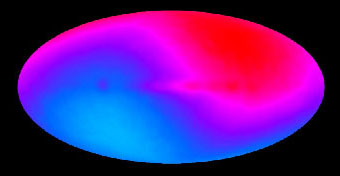
Lorsqu’on observe ce rayonnement brut, on trouve une disymétrie entre deux points opposés du ciel. Ceci, loin de discréditer les données, les renforce et prouve qu’il s’agit bien d’un rayonnement cosmologique : s’il était émis localement, il serait entraîné comme la Terre, et ne montrerait pas cette anisotropie. En effet, la Terre n’est pas immobile dans l’Univers : elle se déplace autour du Soleil, qui tourne autour de la Galaxie, elle-même en mouvement… En combinant ces mouvements, on détermine un point de l’espace vers lequel se dirige la Terre, en allant à la rencontre du rayonnement cosmologique, qui apparaît donc légèrement décalé vers le bleu, c’est-à-dire plus chaud. Dans la direction opposée, on fuit ce rayonnement, qui apparaît donc décalé vers le rouge, c’est-à-dire plus froid. De plus, entre ces deux directions opposées, la température varie en fonction du cosinus de l’angle, exactement comme on s’y attend. Cette anisotropie est de quelques 10-3 en relatif.
On peut donc retrancher cette différence de température fonction de la direction, pour obtenir une carte comme celle montrée ci-dessous, qui est due à WMAP. La direction de ce phénomène est parfaitement compatible avec les mouvements de la Terre dans l’Univers proche.
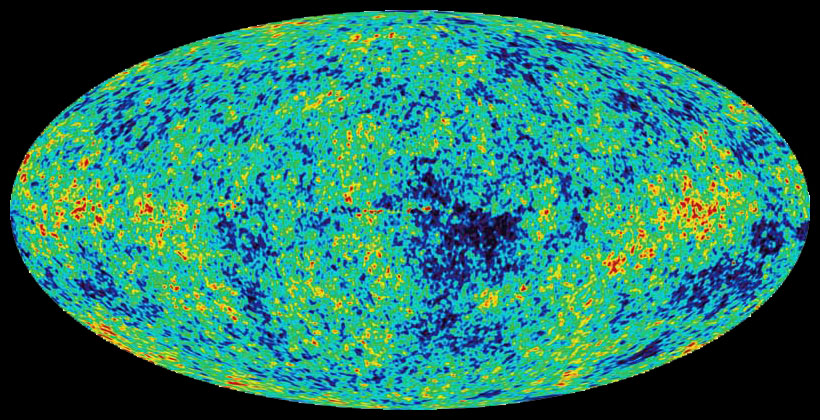
Les fluctuations visibles sur cette carte sont des différences de température de 0,00001° au maximum. Il faut l’aide de la théorie pour déterminer à quelle époque cette lumière a été émise, et dans quelles conditions. C’est en fonction d’un modèle que les résultats peuvent être interprétés. Nous verrons donc d’abord comment construire des modèles, et ensuite nous interpréterons les données observationnelles en fonction de ce modèle. Si le modèle donne une vision cohérente de l’ensemble des données, on pourra le considérer comme représentatif.
A la fin des années 40, Georges Gamow et ses étudiants Ralph Alpher et Robert Hermann, ont étudié les premières phases de l’Univers, lorsque sa température était extrêmement élevée. Ils ont compris que le rayonnement restait piégé dans la matière dense, jusqu’à ce que la densité baisse, avec l’expansion, au-dessous d’un certain seuil. Ils en ont déduit que du rayonnement a été émis alors partout dans l’Univers, et que nous devrions le voir encore aujourd’hui. En 1948, Alpher et Hermann ont publié un article dans lequel ils prédisaient un rayonnement d’une température de 5 K qui devrait couvrir tout le ciel. Malheureusement, leur travail a été totalement oublié… et le prix Nobel est allé à d’autres plus chanceux.
L’interprétation de ce rayonnement confirme les travaux de Georges Lemaître et Alexandre Friedmann, qui ont montré que les solutions des équations d’Einstein (Relativité Générale), ne produisaient que des modèles d’Univers en contraction, ou en expansion, mais en tous cas non stationnaires. L’homogénéité de ce rayonnement en elle-même pose le problème de l’horizon, mais pour l’instant, deux aspects sont à considérer :
Le premier de ces points est délicat, car dans une époque reculée, lorsque l’Univers était très dense, il y avait obligatoirement un équilibre thermique entre la matière et le rayonnement (les collisions permanentes entre photons et particules de matière échangent de l’énergie). Comment se fait-il que cet équilibre ait été rompu ? La matière devrait, en considérant ce seul aspect, être restée tout aussi homogène aujourd’hui. Les modèles devront résoudre ce problème.
Le second point semble montrer que, dès l’époque où ce rayonnement a été émis, il y avait des inhomogénéités de très faible amplitude(10-5). Ce sont des points légèrement plus chauds que le reste du ciel, donc probablement légèrement plus denses. On suppose que ces inhomogénéités sont les amorces de la formation des galaxies. Mais ceci reste à confirmer par des études nouvelles.
Nous avons admis que l’Univers était très condensé, donc très chaud, peu après le début. Nous devons en conclure qu’il rayonnait approximativement comme un corps noir. Et ce rayonnement devait être à courte longueur d’onde, correspondant à la température élevée. Comment se fait-il qu’on observe aujourd’hui un rayonnement à très basse température ? Il faut une explication basée sur les propriétés des ondes.
A partir de la métrique de Robertson-Walker (la métrique mesure les distances), on démontre que la longueur d’onde s’étire comme les distances au cours de l’expansion : λ ∝ a(t), d’où :
λr / λe = a(tr) / a(te)
où λr est la longueur d’onde à la réception, alors que λe est la longueur d’onde à l’émission. Puisque le décalage spectral est défini en fonction de la longueur d’onde comme z = (λr - λe) / λe, on a z + 1 = λr - λe et par suite :
où on considère la réception aujourd’hui avec tr = t0.
La composition chimique de l’Univers est la répartition de la masse selon les différentes espèces chimiques : hydrogène, hélium, carbone, oxygène…
Pour déterminer cette composition, observer celle de la Terre est un très mauvais choix, car lors de sa formation, elle a concentré les éléments lourds. Un meilleur choix est celui du Soleil, qui s’est formé il y a 5 milliards d’années, à partir d’une nuage de gaz plus représentatif. Cependant, ce nuage avait déjà été contaminé par des explosions de supernovæ, et donc sa composition avait été modifiée. Le milieu le plus représentatif de la composition primordiale se trouve en fait dans les grands nuages moléculaires, qui n’ont pas évolué depuis le début de l’Univers.
Leur composition est maintenant bien connue. Elle ne comporte que les éléments les plus légers : hydrogène (et son isotope le deutérium), hélium (4He et un peu de 3He), et lithium. Les autres éléments en sont absents. Cependant, la théorie des étoiles nous montre qu’elles sont capables de synthétiser tous les éléments de l’hélium jusqu’au fer, puis de les répandre dans l’espace lors des violentes explosions de supernovæ. Pour les éléments plus lourds que le fer, leur présence est justifiée par des réactions nucléaires à très énergie qui se produisent pendant l’explosion d’une étoile. Les taux de production mesurés, déduits de la fréquence des explosions et de la quantité de chaque élément que l’explosion peut produire, sont en bon accord avec les observations d’abondances. Par conséquent, tous les éléments en dehors des plus légers cités plus haut sont effectivement produits exclusivement par les étoiles au cours de leur vie ou lors de leur explosion. Il reste quelques éléments légers, comme le bérylium et le bore, trop fragiles pour être synthétisés efficacement par les étoiles, et qui ne sont pas expliqués par la nucléosynthèse primordiale. On les observe dans les rayons cosmiques, mais leur production est expliquée par des réactions de spallation qui détruisent des éléments plus lourds (carbone, azote).
Donc, observant la composition actuelle de l’Univers, et tenant compte de ce qui a été ajouté au fil des temps par les étoiles, on aboutit à une composition simple de l’Univers primordial, contenant seulement les éléments légers cités plus haut. Et de fait, l’histoire de l’Univers, telle qu’on la conçoit aujourd’hui, explique très bien cette composition, et ceci constitue l’une des bases observationnelles de la Cosmologie moderne.
Il reste un ingrédient encore plus insaisissable : l’énergie noire. Depuis une dizaine d’années, on a découvert que l’expansion de l’Univers était accélérée, et non pas ralentie comme on le pensait avant. En effet, l’attraction gravitationnelle cumulée de toutes les galaxies s’oppose à l’expansion, qu’elle freine forcément. D’où le consensus sur un ralentissement. Mais une observation des supernovæ Ia lointaines est venu tout bouleverser. Celles-ci sont produites par l’effondrement gravitationnel d’une naine blanche qui accrète de la matière provenant d’un compagnon de type géante rouge. Lorsque la masse atteint la limite de Chandrasekhar, l’explosion se produit. Les conditions du phénomène, liées à cette masse limite, expliquent bien que la quantité d’énergie dégagée soit la même d’un événement à l’autre. Ces objets peuvent donc servir de chandelle standard pour évaluer les distances, d’autant plus qu’ils sont très lumineux.
Une étude systématique des supernovæ Ia a montré que les plus faibles, donc aussi les plus lointaines et les plus anciennes, sont moins lumineuses que ce que l’on pensait. Il y a deux façons de comprendre cet effet : soit la physique des supernovæ a changé, ce qu’on n’envisage pas vu les indications données plus haut, soit la distance à laquelle elles se trouvent est à revoir. C’est bien sûr cette seconde hypothèse que l’on privilégie, et qui montre que les distances dans l’Univers ont augmenté plus que ce que l’on croyait. Donc que l’expansion a été plus rapide que ce qu’on croyait auparavant. Cette accélération a commencé il y a quelques milliards d’années.
La question est maintenant de comprendre d’où vient l’énergie qui permet cette accélération ? N’ayant a priori aucune explication sous la main, on invoque là encore une composante mystérieuse de l’Univers, que l’on nomme énergie noire, et qui n’est mise en évidence que de cette façon.
On remarquera que matière noire et énergie noire sont toutes deux mises en évidence par des phénomènes dynamiques. Et toutes deux dépendent étroitement, pour leur explication, des théories physiques actuelles les plus poussées, et par là-même les plus spéculatives. Mais pour l’instant, nous n’avons pas le choix… Peut-être les résultats à venir du LHC pourront-ils nous éclairer sur l’un, voire les deux mystères !
D’après ce qui vient d’être dit, et que de très nombreuses études appuient, l’Univers est constitué de :
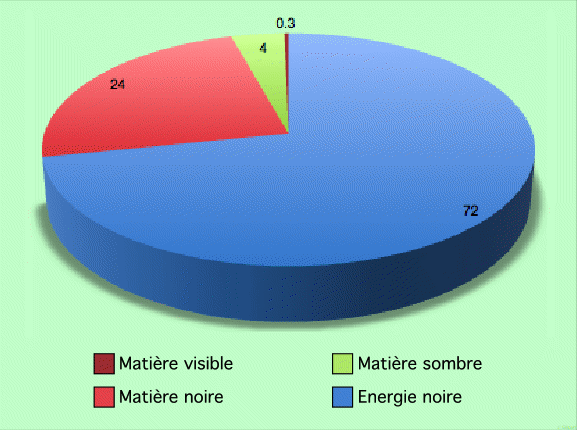
Si tout ceci donne plus de 100 %, ce n’est pas grave : les valeurs données sont bien évidemment approchées…
Attention La différence entre la matière visible et la matière sombre réside simplement dans les conditions physiques, qui font que la première brille et la seconde pas. La matière visible est constituée essentiellement d’atomes, construits avec des protons et des neutrons. Ces particules sont nommées collectivement des baryons. Aussi, la matière que nous connaissons est-elle nommée matière baryonique. Par opposition, la matière noire, complètement hypothétique à l’heure actuelle, est nommée matière non baryonique. En effet, si elle était faite de protons, elle brillerait, ou absorberait la lumière, et nous la verrions !
Remarque philosophique : Copernic nous a chassés du centre de l’Univers, en y plaçant le Soleil. Les astronomes ont ensuite détrôné le Soleil, tant par sa position non centrale, que par ses mensurations qui n’en font qu’une étoile tout à fait ordinaire. Voilà que maintenant, la matière dont nous sommes faits n’est plus qu’une infime partie de ce qui constitue l’Univers ! Décidément, nous devrions être bien modestes…
| L’Univers contient donc la matière ordinaire brillante, la matière ordinaire sombre, plus une matière totalement inconnue et largement majoritaire, qui ne se manifeste à nous que par les perturbations gravitationnelles qu’elle produit. Les physiciens des particules recherchent activement cette dernière matière, et les instruments installés autour du LHC pourraient bientôt nous apporter quelques éclaircissements sur ce sujet. Toutefois, quelques irréductibles astronomes pensent que la matière noire n’a jamais existé ailleurs que dans l’imagination des théoriciens. On ne l’a en effet invoquée que pour résoudre un problème de dynamique. Ce problème aurait-il une autre solution ? C’est la direction dans laquelle se sont engagés certains théoriciens en proposant des théories de gravitation newtonienne modifiée. Mais à ce jour, les résultats ne sont pas à la hauteur de leurs espérances. Il faut toutefois reconnaître que notre connaissance de la gravité est limitée au voisinnage du Soleil. Serait-elle différente à plus grande distance ? |
La Cosmologie moderne s’appuie sur les trois piliers observationnels vus ci-dessus :
Une critique de ce paradigme est en préparation. Elle sera mise en ligne prochainement.
L’interprétation de ces trois observations montre qu’elles ne concernent pas la même époque. L’expansion est observée telle qu’elle est aujourd’hui, sans nous renseigner sur les valeurs passées du taux d’expansion.
Par contre, le fond de rayonnement est un vestige de l’époque à laquelle l’Univers est devenu transparent, ce qui remonte à 380.000 ans après le début de l’expansion. Son observation nous renseigne donc sur une époque précise, et nous donne ainsi un point fixe pour les modèles.
Enfin, la composition chimique primordiale provient d’une période où les réactions nucléaires ont pu se produire dans un Univers juste assez chaud pour cela. Ensuite, elles ont cessé et la composition n’a plus changé. Elles témoignent donc de cette période, de courte durée, et située encore bien avant l’émission du fond cosmologique.
Par conséquent, ces trois piliers des modèles de Big Bang sont non seulement des faits à expliquer, mais aussi des dates à respecter. Et leur enchaînement nous fixe une partie de l’histoire de l’Univers.
Les idées essentielles pour concilier toutes les observations dérivent tout d’abord de l’expansion, vue à l’envers. En supposant qu’un film ait été fait depuis des milliards d’années, et qu’on puisse passer ce film à l’envers en (très très) accéléré, on verrait les galaxies se rapprocher les unes des autres. Viendrait un moment où elles se rejoindraient (peut-être seulement la matière qui les constitue), en une masse indifférenciée. Celle-ci se condenserait encore jusqu’à… peut-être un état de densité infinie. C’est en tous cas ce que donne une approximation qui ne considère pas la physique des premiers temps, d’ailleurs inconnue.
Cette condensation est à l’origine des modèles de Big Bang, initiés par l’atome primitif de Georges Lemaître.
Mais les choses ne sont pas si simples. Considérer que l’Univers a débuté dans un état de condensation extrême, et s’est dilué au fil du temps jusqu’à sont état actuel, pose plusieurs problèmes de compatibilité : comment l’état initial peut-il conduire à l’état actuel ? Certaines propriétés sont difficiles à expliquer.
A l’heure actuelle, la gravité est une force extrêmement faible, qui n’arrive à régner que dans des milieux où la matière est très condensée, l’Univers globalement étant de densité dérisoire. Mais en passant le film à l’envers, et s’approchant du début, on constate que la densité moyenne de l’Univers était très forte, et que par conséquent, la gravitation jouait un rôle important. Dans ces conditions, nous devons utiliser une théorie de la gravitation comme base de toute théorie cosmologique.
La Gravitation Universelle de Newton a été utilisée dans ce but, mais elle a posé des problèmes liés à ses bases mêmes, qui en ont empêché le développement.
La Relativité Générale, publiée en 1915, a été appliquée à la cosmologie très rapidement. Représentant la gravitation comme une déformation de l’espace-temps par les masses présentes, elle fournit un cadre bien adapté à l’étude de l’Univers à grande échelle, et se trouve à la base des théories cosmologiques modernes.
Elle considère qu’en tout point, l’Univers (à grande échelle) présente une courbure spatiale, la même partout. Mais des considérations théoriques que nous verrons plus loin, confrontées aux mesures de densité, indiquent que la courbure est proche de zéro. Nous verrons aussi que ceci est difficile à justifier…
Nous allons successivement établir les bases théoriques de la cosmologie, puis en déduire des modèles simples. L’analyse de ces modèles confrontés aux observations, pose un certain nombre de problèmes. Leur solution passera par une modification du modèle de base, en lui ajoutant une période d’inflation, pendant laquelle les distances dans l’Univers ont crû exponentiellement.
La création d’une paire particule-antiparticule fait apparaître une masse qui est le double de la masse de la particule (particule et antiparticule ont la même masse). Pour créer une paire, il faut donc disposer d’une énergie au moins égale à leur énergie de masse totale. Par conséquent, la température, qui est équivalente à l’énergie du milieu, doit dépasser une température plancher correspondant à la masse des particules. Tant que le milieu est bien au-dessus de cette température, des paires se créent donc en abondance. Mais le milieu est aussi très dense, et une particule rencontre rapidement son antiparticule. Elles s’anihilent donc, en restituant l’énergie qui avait servi à leur création. Plus il y a de créations, plus il y a de particules et d’antiparticules, donc plus les chances de rencontres augmentent. Par conséquent, plus il y a de création, plus il y a d’annihilations, et il se crée un équilibre. Cet équilibre est caractérisé par une certains abondance des particules de ce type.
Si l’énergie du milieu est très élevée (donc aussi sa température), plusieurs types de particules peuvent exister en équilibre. Des interactions fréquentes entre toutes ces particules assurent l’équilibre thermique. Celui-ci est produit par les échanges d’énergie entre les particules qui interagissent : les moins énergétiques en gagnent, les plus énergétiques en donnent.
Considérons une particule de masse m, que l’on exprimera en unités d’énergie (MeV ). Ceci est possible en vertu de l’équivalence E = m c2. Si l’énergie disponible dans l’Univers est supérieure à deux fois l’énergie de masse d’une particule, elle peut produire une paire particule-antiparticule.
Considérons par exemple l’électron. Sa masse est m0 = 9,11 10-31 kg, qui correspond à une énergie de 0,511 Me V / c2 (0,511 MeV = 9,11 10-31 kg × c2). Pour créer un électron et son antiparticule positron (qui possède la même masse), il faut donc 2 × 0,511MeV , soit 1,022 MeV . Si l’énergie disponible est supérieure, c’est-à-dire si la température est au-dessus d’un milliard de K, alors des paires électron-positron peuvent se créer à partir de cette énergie.
Mais la densité est forte, et la probabilité qu’un électron rencontre un positron est donc aussi très élevée : la rencontre est aussi certaine que la création de la paire. En se rencontrant, l’électron et le positron s’annihilent (toujours par l’équation E = m c2) et restituent l’énergie qui avait servi à les produire. L’ensemble de ces deux réactions : création-annihilation, est une relation d’équilibre.
A un instant donné, il vient de se créer un certain nombre de couples électron-positron, mais il faut un peu de temps à ces particules pour se rencontrer et s’annihiler. Ce petit délai est suffisant pour qu’il existe, à chaque instant, quelques particules de chaque espèce, électrons et positrons.
Toutes les réactions d’équilibre maintiennent donc une proportion plus ou moins importante de couples de particules.
Dans ce qui précède, nous avons considéré une température particulière. Que se passe-t-il si la température baisse ? L’énergie disponible baisse tout autant. Et à force de baisser, elle se retrouve en-dessous de l’énergie nécessaire à la création de paires. Celle-ci stoppe donc. Mais l’annihilation qui les détruit n’a aucune raison de cesser ! Ce raisonnement nous amène à la conclusion que toutes ces particules doivent se détruire, il ne doit plus en rester une seule …
La matière existe pourtant ! L’explication provient sans doute (mais ceci est encore du domaine de la recherche), d’une disymétrie de désintégration des particules : les antiparticules ont une probabilité de se désintégrer légèrement supérieure (un milliardième …). Par conséquent, lorsque la température a baissé, certaines particules et antiparticules se désintègrent, avant de pouvoir s’annihiler. Et comme les antiparticules se désintègrent un peu plus, il restera finalement quelques particules. Exactement, pour un milliard de particules et un milliard d’antiparticules, il reste un seule particule. C’est-à-dire que l’Univers pourrait être beaucoup plus dense si la différence de probabilité était plus importante, ou tout simplement vide de matière si elle était nulle.
Le premier problème qui se pose, avant d’aborder une théorie, est de caractériser ce que nous observons. Nous sommes sur Terre, en un point particulier de l’Univers, et nous ne pouvons pas nous en échapper pour observer d’un autre point de vue. Nous n’aurons jamais qu’un seul regard, il nous est impossible de savoir comment se présente l’Univers aux hypothétiques habitants d’une lointaine galaxie. Les seules observations possibles, depuis notre coin d’Univers, sont en profondeur.
Les observations que nous pouvons faire nous montrent un Univers qui a le même aspect, globalement, dans toutes les directions où l’on regarde, au moins en regardant assez loin pour gommer les irrégularités locales. Ceci a amené les astronomes à considérer, et à poser comme premier principe, que l’Univers est isotrope, ce qui signifie qu’il a le même aspect dans toutes les directions, vu depuis la Terre. Un Univers isotrope pourrait très bien présenter une densité décroissante depuis le centre où nous l’observons, en fonction de la distance. Mais une telle configuration nous donnerait une position privilégiée, que les astronomes ne sont pas prêts à admettre sans preuves.
Puisque la Terre ne joue pas de rôle privilégié, il doit en être de même partout ailleurs, et l’Univers doit être isotrope de tous les points d’observation.
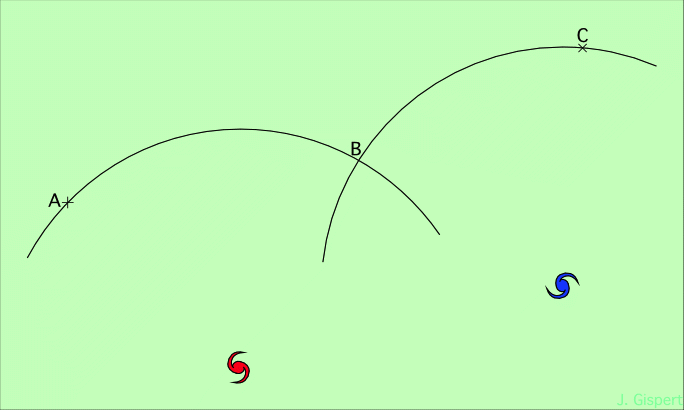
L’isotropie de l’Univers en tous points entraîne son homogénéité.
De la galaxie rouge, les points A et B, situés à la même distance, mais dans des directions différentes, ont donc les mêmes propriétés (isotropie de l’Univers autour de la galaxie rouge). De la galaxie bleue, on peut dire que les points B et C ont aussi les mêmes propriétés (isotropie autour de la galaxie bleue). Donc, les points A et C ont aussi les mêmes propriétés. Vu de la galaxie rouge, C n’est pas à la même distance que A et B, et pourtant ses propriétés sont identiques. L’isotropie autour des deux galaxies implique donc l’identité de propriétés entre des points non situés à la même distance. Le point C ayant été pris arbitrairement, on peut en déduire que tous les points de l’Univers ont les mêmes propriétés, c’est-à-dire que l’Univers est homogène.
Ce raisonnement nécessite toutefois, pour être correctement applicable, de connaître la distance, même si celle-ci n’est pas obtenue avec une très grande précision.
Ce n’est qu’un principe, car il s’appuie sur une propriété postulée : nous n’occupons pas un point privilégié de l’Univers.
Il a l’avantage de rendre les équations beaucoup moins difficiles (quoique la difficulté n’ait pas disparu pour autant). Cependant, il faut garder en tête les limitations de ce principe, puisque l’homogénéité de l’Univers n’apparaît réellement qu’à des échelles supérieures à la centaine de méga-parsecs… Ignorer, dans les équations, toutes les turbulences locales (dans les galaxies et les amas de galaxies) est une approximation importante, de nature à affaiblir quelque peu les conclusions des modèles ainsi construits, mais qui se justifie à très grande échelle. Il y aura donc encore longtemps du travail pour les jeunes cosmologistes ! La matière sur laquelle ils travaillent est jeune aussi, et n’a pas encore bien affirmé son caractère.
Puisqu’il y a un début, qui se situe vers 13,7 milliards d’années (ordre de grandeur), rien n’a pu se propager dans l’Univers plus longtemps. Aussi, toute lumière qui nous parvient aujourd’hui a été émise au plus tôt il y a 13,7 milliards d’années. La vitesse de la lumière étant une constante absolue, un objet situé plus loin que 13,7 milliards d’années-lumière n’a pas eu le temps de nous éclairer, aussi se trouve-t-il au-delà de notre horizon (l’horizon est ce qui limite la vue). L’ensemble des objets qui ont eu le temps de nous envoyer un signal constitue l’Univers observable.
Lorsqu’on jette une pierre dans l’eau, elle produit une onde circulaire (des ronds dans l’eau) qui s’étend à partir du point de chute P. Cette onde est analogue de l’Univers observable sur la surface du bassin. Avant que la pierre ne tombe, tous les points de la surface du bassin existent. A partir de la chute, l’onde se propage et atteint des points de plus en plus loin, à mesure qu’elle avance.
Remarque : s’il n’y a pas eu d’instant zéro stricto sensu (pas de singularité), la surface de dernière diffusion (voir plus loin) en tiendra lieu.
Attention :
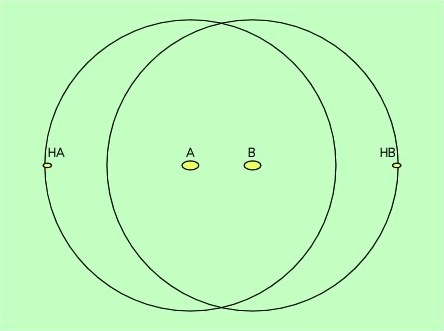
Le schéma ci-dessous montre deux galaxies A et B, desquelles on observe l’Univers. La galaxie HA est située à la limite de l’Univers observable pour A : si elle était située un peu plus loin, sa lumière n’aurait pas eu le temps de parvenir en A. Il est aisé de constater que cette même galaxie HA est hors de portée de la galaxie B, puisque sa distance à B est égale à sa distance à A, augmentée de la distance AB.
Puisque la lumière parcours 300.000 km supplémentaires à chaque seconde, le cercle représentant l’Univers observable de chacune des galaxies s’accroît ; il viendra un jour où la galaxie HA sera englobée dans l’Univers observable de B, il suffit d’avoir de la patience…
Partant de 0, le rayon de l’Univers observable à un instant t donné est donc c t, où c est la vitesse de la lumière. Puisque cette vitesse est la même dans toutes les directions, l’Univers observable en A est une sphère de rayon c t centrée sur A.
Cette notion d’Univers observable est fondamentale dans notre compréhension de l’Univers : nous n’en voyons de toutes façons qu’une petite partie, forcément finie ! La question de savoir si l’Univers est infini est donc hors de portée de nos observations directes.
L’étude des amas de galaxies, et des structures à plus grande échelle encore (super-amas…), nous rapproche des limites de l’Univers observable. Elle a donc inéluctablement des conséquences sur la cosmologie.
La vitesse de la lumière étant absolue, la lumière qui est partie de notre région il y a 13,7 milliards d’années atteint aujourd’hui les points les plus éloignés que nous pouvons observer. L’Univers observable est donc la sphère d’influence qui nous concerne : tout ce qui est en dehors ne nous a jamais influencé, et n’a jamais été influencé par nous.
L’existence d’un horizon et l’expansion, mises ensemble posent un problème.
L’horizon grandit aujourd’hui plus vite que l’expansion (puisque la vitesse de la lumière est très supérieure à la vitesse d’expansion). Symétriquement, si on remonte le temps vers le Big Bang, l’horizon diminue plus vite que l’expansion. Par conséquent, la portion d’Univers que nous voyons aujourd’hui est bien plus grande que celle que l’on aurait pu voir peu de temps après le Big Bang, disons au moment où a été émis le rayonnement cosmologique.
Pour le comprendre, considérons un instant proche du début de l’Univers, où son âge est, disons, d’une année. L’horizon d’un observateur s’étend à une année-lumière autour de lui. Si on considère l’Univers âgé d’une minute, l’horizon n’est plus qu’à une minute-lumière, c’est-à-dire à 18 millions de kilomètres. C’est bien moins que la distance de Mercure au Soleil. A cette époque-là, aucun signal, aucune information, n’avait pu franchir une distance plus grande. Deux points situés alors à 36 millions de kilomètres l’un de l’autre par exemple, n’ont pas pu échanger de signaux. La température de l’un est par conséquent sans aucun rapport avec la température de l’autre. Ceci va constituer l’un des grands problèmes posés à la théorie du Big Bang, puisque le fond de rayonnement cosmologique est remarquablement égal sur tous les points de la sphère céleste. Ceci signifie que la température était partout égale dans l’Univers à ce moment-là. Qu’est-ce qui a bien pu égaliser la température avec cette précision, en des points inaccessibles les uns aux autres ?
Les théories de Big Bang élémentaires ne le résolvant pas, il faudra recourir à l’inflation pour expliquer cela.
La cosmologie vise à caractériser l’état initial de l’Univers, et son évolution. Cette évolution, appliquée à l’état initial choisi, doit donner l’état actuel, tel qu’il est observé. Si ce n’est pas le cas, il faut remettre en cause, soit l’état initial, soit l’évolution, soit les deux !
Pour ce qui est de l’état initial, il nous est actuellement impossible de l’observer (si l’observation devient possible un jour, et s’il existe un véritable état initial, ce qui ne serait pas le cas si l’Univers avait toujours existé). Mais la radioastronomie nous a donné une image bien précise de l’état de l’Univers il y a plus de 13 milliards d’années, et cet état est un jalon précieux pour évaluer les modèles. Peu de temps après cette date reculée, les galaxies (et surtout les quasars) deviennent observables, et nous renseignent sur les états intermédiaires. Nous disposons donc d’une image bien précise de l’évolution de l’Univers, au moins sur cette longue période.
L’homogénéité de l’Univers (principe cosmologique) indique que la composition, la température, la pression, etc., sont les mêmes partout. On admet aussi que les lois de la physique sont universelles (dans l’espace et dans le temps). Alors, puisque tous les points de l’Univers étaient à l’origine dans le même état, et ont subi les mêmes lois, leur évolution a été la même. Ce qui revient à dire qu’ils partagent la même Histoire. L’Histoire se décrit en fonction du temps, et l’identité de l’Histoire implique l’identité du temps. Le temps cosmique ainsi défini est celui d’un quelconque observateur, choisi arbitrairement. Puisque l’évolution est la même pour tous, il est représentatif.
Ce temps n’est pas en contradiction avec la Relativité. Il décrit comment l’Univers a évolué en tout point, et ne définit aucune relation entre deux points différents. Alors que la Relativité nous dit comment on peut passer d’un point à un autre.
Nous allons présenter un ensemble d’équations qui représente l’équilibre de l’Univers, et dont on pourra tirer les propriétés de ce dernier. Les méthodes utilisées sont les grandes lois de la physique, appliquées au cas particulier considéré. On peut utiliser pour cela soit les lois newtoniennes, soit les lois relativistes. Mais pour une représentation vraiment correcte, seules les lois relativistes sont pertinentes.
Les coordonnées comobiles sont des coordonnées entraînées avec l’expansion de l’Univers, que l’on a définies à propos de la Relativité Générale. Etant donné que la Cosmologie utilise la Relativité Générale avec les métriques adaptées, les coordonnées comobiles s’imposent et seront d’usage courant.
Notons r(t) la distance à l’instant t entre les deux galaxies, et x la distance comobile entre elles. L’une varie, l’autre non. Notons a(t) la proportion entre les deux :
r(t) = a(t) x
On appelle facteur d’échelle la fonction a(t). Elle décrit l’expansion de l’Univers en fonction du temps. r(t) et x sont des longueurs, donc a(t) n’a pas de dimensions.
Le principe cosmologique, qui affirme l’homogénéité de l’Univers, rend le facteur d’échelle indépendant des coordonnées d’espace ! C’est pourquoi il a été noté seulement dépendant du temps.
Friedmann a écrit une équation qui représente l’équilibre de l’Univers, considéré comme un gaz de galaxies. Cette approximation est communément utilisée depuis.
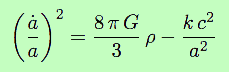
Dans cette équation, a est le facteur d’échelle, la notation ![]() représente la vitesse d’évolution du facteur d’échelle (c’est la dérivée de a par rapport au temps). Donc,
représente la vitesse d’évolution du facteur d’échelle (c’est la dérivée de a par rapport au temps). Donc, ![]() est la vitesse relative (en pourcentage). G est la constante newtonienne de la gravitation universelle, ρ la densité de matière (partout la même puisqu’on considère l’Univers homogène, d’après le Principe Cosmologique), enfin k est une constante.
est la vitesse relative (en pourcentage). G est la constante newtonienne de la gravitation universelle, ρ la densité de matière (partout la même puisqu’on considère l’Univers homogène, d’après le Principe Cosmologique), enfin k est une constante.
Cette équation peut s’obtenir à partir de la théorie de Newton, aussi bien que de la Relativité Générale. La version relativiste peut toutefois contenir un terme supplémentaire, la fameuse constante cosmologique Λ :
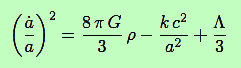
Dans l’équation de Friedmann, 8 π G / 3, c2 et Λ sont des constantes. Elle relie donc le facteur d’échelle a, la densité ρ, et la constante k. Du fait de l’homogénéité de l’Univers, k est aussi une constante. Donc, il ne reste que deux variables : a et ρ. L’équation n’est pas suffisante, à elle seule, pour décrire complètement l’évolution de l’Univers (elle le serait si on connaissait l’évolution de ρ).
Il nous faudra donc au moins une nouvelle équation pour déterminer complètement le problème. Cette équation nous donnera l’état de la matière dans l’Univers.
L’équation de Friedmann (sans constante cosmologique) s’obtient en physique newtonienne. Le terme de gauche dérive de l’énergie cinétique d’une particule, le premier terme de droite provient de l’énergie potentielle de la particule, et le dernier représente l’énergie totale. k n’a pas de signification particulière. L’équation de Friedmann s’obtient donc tout simplement en écrivant que l’énergie totale reste inchangée puisque l’Univers est un système fermé. C’est une application immédiate de la conservation de l’énergie en mécanique classique.
L’équation de Friedmann s’obtient aussi en Relativité Générale. L’équation des champs d’Einstein s’écrit Gμν = -8 pi G Tμν où Gμν représente la géométrie de l’espace-temps, et Tμν son contenu en matière-énergie. C’est une équation tensorielle d’ordre 4 (les tenseurs sont des tableaux de nombres de 4 × 4). Le tenseur d’Einstein Gμν est construit pour satisfaire à la conservation de l’énergie. Il n’est donc pas étonnant que l’équation non relativiste de Friedmann s’y retrouve, puisqu’elle a été produite sur les mêmes arguments. L’équation de Friedmann est le terme 00 de l’équation d’Einstein. La constante k représente alors la courbure de l’espace-temps :
Dans un espace à géométrie euclidienne (plat, k = 0), la somme des angles d’un triangle vaut deux droits (180°), et la circonférence vaut 2 π r.
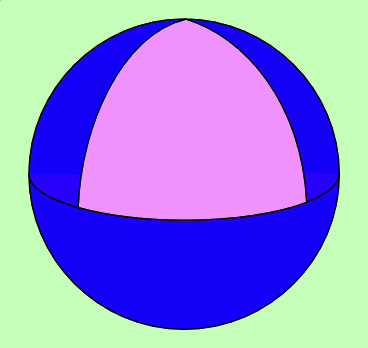
Mais dans une géométrie sphérique, la somme des angles d’un triangle excède 180° (prenez un triangle rectangle au pôle nord, et s’étendant jusqu’à l’équateur : il est également rectangle en ses deux sommets sur l’équateur, donc il possède trois angles droits). La circonférence est inférieure à 2 π r.
Enfin, dans une géométrie hyperbolique, c’est tout le contraire : la somme des angles d’un triangle est inférieure à 180°, et la circonférence est supérieure à 2 π r.
Pour obtenir l’équation du fluide, c’est-à-dire celle concernant l’évolution de la pression, on utilise tout simplement la première loi de la Thermodynamique. Celle-ci relie l’énergie interne d’un système, au travail des forces de pression, et à la quantité de chaleur échangée avec l’extérieur :
dE + p dV = T dS
où dE est la variation d’énergie interne, p la pression, dV la variation de volume, T la température, et dS la variation d’entropie.
Dans le cas de l’Univers, il n’y a pas d’extérieur, donc pas d’échange possible. Par conséquent, dS = 0, et il reste :
dE + p dV = 0
On considère que le volume est sphérique, de rayon a. Alors V = 4/3 π a3. On en déduit immédiatement dV/dt = 4/3 π 3 a2 da/dt.
D’autre part, en notant ρ la masse volumique, on peut écrire la masse m = ρ V = 4/3 π a3ρ. En vertu de l’équation d”Einstein E = m c2, on a donc :
E = 4/3 π a3 ρ c2
dE/dt = 4/3 π 3 a2 da/dt ρ c2 + 4/3 π a3 c2 dρ/dt
En reportant les expressions de dE/dt et dV/dt dans l’équation de base on obtient :
4/3 π 3 a2 da/dt ρ c2 + 4/3 π a3 c2 dρ/dt + p 4/3 π 3 a2 da/dt = 0
| On simplifie par 4/3 π a2 : | 3 da/dt ρ c2 + a c2 dρ/dt + p 3 da/dt = 0 | |
| On divise tout par c2 : | 3 da/dt ρ + a dρ/dt + p/c2 3 da/dt = 0 | |
| On met en facteur les deux termes contenant la dérivée de a : | 3 (ρ + p/c2) da/dt + a dρ/dt = 0 |
Enfin, on divise par a, et on remplace les dérivées par la notation en point :
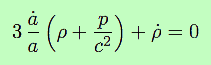
C’est l’équation du fluide, qui donne une relation entre le facteur d’échelle a, la pression p et la densité du milieu ρ.
On peut s’assurer que l’équation de Friedmann et l’équation du fluide ne suffisent pas encore à déterminer totalement le problème. Pour cela, il nous manque une contrainte entre la pression et la densité, ce qui s’appelle une équation d’état.
L’équation d’état dépend des conditions physiques qui règnent dans le milieu considéré. Précisément, on considère trois sortes de situations :
L’équation d’état associée est :
| prépondérance du rayonnement | p = 0 |
| prépondérance de la matière | p = ρ c2 / 3 |
| prépondérance du vide | p = -ρΛ c2 |
Dans les circonstances générales, où aucun élément ne dominerait les autres, l’équation d’état à considérer est un mélange de toutes les contributions.
L’équation d’état du vide peut paraître bien surprenante. ρ y représente la densité d’énergie du vide qui correspond à la constante cosmologique. ρ est par conséquent aussi une constante.
Tant qu’on ne pense pas à l’expansion de l’Univers, pas de problème. Mais si on la considère, on remarque que, lorsque les dimensions doublent, les volumes sont multipliés par 8. Puisque la densité d’énergie est constante, chaque centimètre cube du volume dilaté contient la même énergie que chaque centimètre cube du volume original. Et comme il y a 8 fois plus de centimètres cube, il y a 8 fois plus d’énergie…
Une conséquence fondamentale de ceci est que, même très faible, la contribution de la constante cosmologique se multiplie en même temps que l’espace au cours de l’expansion, alors que les autres énergies se diluent… Et forcément, elle finira par devenir prépondérante.
Selon les circonstances dans lesquelles nous considérerons le problème, nous devrons donc ajouter une telle équation adaptée pour pouvoir le résoudre totalement. Ainsi, l’étude des modèles cosmologiques se réduit à la résolution de trois équations :
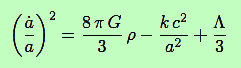 |
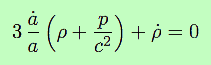 |
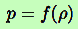 |
Nous reprendrons ces équations pour obtenir les modèles.
Nous allons détailler quelques situations particulière, la dernière seulement présentant une constante cosmologique non nulle.
La vitesse de récession est proportionnelle à la distance : v = H r, en conservant la notation r pour la distance. On peut écrire d’autre part, puisque la vitesse est un vecteur :
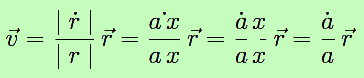
Avec v = H r on déduit :
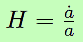
En reportant dans l’équation de Friedmann, on obtient la nouvelle forme de cette dernière :
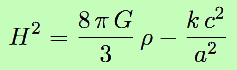
On appelle densité critique de l’Univers celle pour laquelle il serait plat, sans courbure. D ; donc lorsque k = 0 dans l’équation de Friedmann. En faisant le calcul, on trouve :
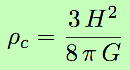
Faisant le calcul pour H0 = 72 km s-1 Mpc-1, on obtient :
ρc = 0,974 10-26 kg m-3, soit pratiquement 10-26 kg m-3. C’est la valeur annoncée plus haut.
On peut voir cette valeur sous un angle différent, en changeant d’unités : au lieu des kg m-3, passons à des masses solaires et des méga parsecs. Ces unités-là sont représentatives de l’Univers. La conversion donne :
ρc = 2,938 1011 M Mpc-3
Cette valeur est remarquable. Nous avons vu que la masse typique d’une galaxie est de l’ordre de l’ordre de 1011 M. Or les distances entre les galaxies sont de l’ordre du mégaparsec… Donc la densité de l’Univers est de l’ordre de 1 galaxie par Mpc3, soit 1011 M Mpc-3.
La densité mesurée de l’Univers est donc proche, à un petit facteur près, de la densité critique. On aurait très bien pu trouver une valeur 10.000 fois plus grande ou plus petite, et ce n’est pas le cas.
L’évaluation donnée est actuellement trop grossière pour conclure, les incertitudes trop grandes. Mais cette proximité de la densité critique ne peut être un hasard. Puisque la densité critique est celle d’un Univers plat, l’Univers réel doit être de courbure très faible…
ρvis = 0,27 10-31 g cm-3 ; ρc = 0,974&6 10-26 kg m-3 = 0,974&6 10-29 g cm-3, la proportion de masse visible par rapport à la masse critique est :
Ωvis = ρvis / ρc = 0,27 10-31 g cm-3 / 0,974 10-29 g cm-3 = 0,277 10-2
La densité de matière visible n’est donc que de l’ordre de 0,3 % de la densité critique.
Dans ces conditions, l’expansion devrait largement l’emporter, et l’Univers devrait se diluer indéfiniment. En effet, la densité sépare les modèles d’univers selon leur courbure :
La densité critique est donc un point de repère important, qui permet de savoir, à condition de mesurer correctement la densité de l’Univers, quel sera l’avenir de celui-ci.
Au lieu de la densité visible, il faudra considérer la densité totale de l’Univers, comprenant la matière visible (celle qui rayonne), la matière sombre (matière ordinaire qui ne rayonne pas), la matière noire, et même la densité d’énergie. Puisque l’équation de la Relativité Restreinte E = m c2 traduit l’équivalence entre la matière et l’énergie, l’énergie elle-même, celle des photons, intervient dans l’éventuel freinage de l’expansion.
On note ΩT = ρT / ρc le rapport de la densité totale à la densité critique. L’avenir de l’Univers sera donc déterminé selon que ΩT sera plus petit, égal ou plus grand que 1.
Résoudre directement l’équation de Friedmann est une tâche bien difficile dans toute sa généralité, car les termes décrivant le contenu de l’Univers produisent des variations d’importance différente, et même parfois de sens opposé. La situation serait bien simplifiée si certains termes n’étaient pas présents. On ne peut évidemment pas les supprimer sans trahir l’interprétation physique de cette équation. Mais on peut envisager des circonstances particulières dans lesquelles, éventuellement, certain(s) terme(s) pourrai(en)t avoir une valeur très petite, négligeable devant celle d’un autre. Alors, on pourrait, sans faire une erreur grossière, négliger ce(s) terme(s).
Justement, les trois situations évoquées plus haut, définies par l’équation d’état, sont particulières en ce sens que l’une seulement des trois composantes de l’Univers y est importante, les autres négligeables. Pour la première, le rayonnement, c’est-à-dire les photons et les particules relativistes, domine la matière non relativiste et l’énergie du vide ; pour la deuxième, c’est la matière non relativiste qui domine ; la troisième enfin est applicable lorsque l’énergie du vide supplante la matière non relativiste et le rayonnement. Chacune de ces situations concerne une période de l’Univers, nous verrons plus loin dans quelles circonstances, et nous allons en étudier les principales propriétés.
Ces solutions sont intéressantes, en particulier lorsqu’on fait tendre t vers l’infini, car elles nous dévoileront ainsi le destin de l’Univers (à condition naturellement que les équations le décrivent correctement, et pour savoir cela, on s’appuie sur le passé).
Ces deux cas sont très semblables, et nous allons les étudier en considérant que k = 0, c’est-à-dire que l’Univers est plat (courbure nulle). Cette hypothèse est très proche de ce que nous connaissons à l’heure actuelle par les observations. Dans les deux cas, la pression est négligeable, et donc nous pourrons écrire l’équation d’état sous la forme vraiment simple : p = 0. Cette approximation est dite poussière, parce que la matière condensée en poussières présente une pression bien plus faible (voire nulle) que la même densité sous forme de gaz. Puisque l’énergie est basse, il s’agit de matière non relativiste.
| Equation de Friedmann | Equation du fluide | Equation d’état |
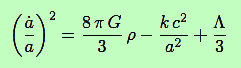 |
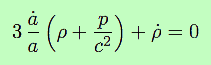 |
| L’équation du fluide se réécrit, puisque p = 0 : |
| C’est une équation à variables séparées, qui se met sous la forme : |
et dont la solution est : Log ρ = -3 Log a + Log m = Log (m a-3), donc ρ = m a-3 ; m est la constante d’intégration
Pour la valeur t = 0, on a a = 1. Donc ρ0 = m et en remplaçant m par ρ0 :
![]()
Ce résultat intermédiaire semble tout à fait évident : la densité baisse comme l’inverse du cube du rayon, c’est-à-dire comme l’inverse du volume de l’Univers. C’est tout à fait ce à quoi on aurait pu s’attendre.
Maintenant que nous avons l’expression de ρ, nous pouvons la reporter dans l’équation de Friedmann, avec toujours k = 0 et Λ = 0 :
| on en tire immédiatement : |
qui s’intègre en : |
On peut mettre cette solution sous une forme plus simple, en ignorant la constante ; puis on reporte le résultat dans l’expression de ρ, et enfin on détermine H :
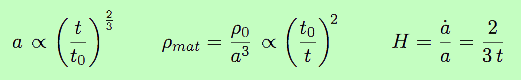
Ces trois formules représentent donc le premier modèle résolu, dans le cas ou la pression est négligeable.
NB. Le symbole ∝ signifie : proportionnel à. Ainsi, a ∝ ( t / t0)2/3 signifie : a est proportionnel à ( t / t0)2/3, ou encore :il suffit de multiplier toutes les valeurs de (t / t0)2/3 par une même constante pour obtenir a. Cette notation évite simplement d’écrire la constante. Elle donne l’essentiel, qui est le comportement de la fonction.
Considérons maintenant le cas où l’Univers serait vide de matière non relativiste, et rempli seulement de rayonnement. La constante cosmologique sera encore nulle. Ici, le rayonnement englobe la matière relativiste, pour laquelle l’énergie cinétique est supérieure à l’énergie de masse. Dans ce cas, l’équation d’état adaptée est la même que pour le véritable rayonnement.
En considérant l’équation d’état appropriée pour le rayonnement, le système à résoudre est :
| Equation de Friedmann | Equation du fluide | Equation d’état |
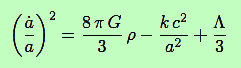 |
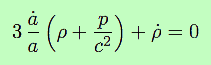 |
| Faisant les mêmes calculs que précédemment, avec cette nouvelle équation d’état, en reportant la valeur de p dans l’équation du fluide, on arrive à : |
| C’est une équation à variables séparées, qui s’intègre immédiatement en : | Log ρ = -4 Log a + Log m = Log m a-4 ⇒ ρ = m a-4 |
Ce résultat peut surprendre. Le volume augmente comme a3, et la densité de rayonnement baisse comme a4. Mais il faut comprendre qu’avec l’augmentation des longueurs, les longueurs d’onde aussi augmentent, et comme l’énergie d’un photon est proportionnelle à sa longueur d’onde, les photons perdent de l’énergie dans l’expansion (l’énergie se dilue). On a donc la contribution en 1/a3 pour l’augmentation de volume, et la contribution en 1/a pour la baisse d’énergie des photons. Le résultat, produit des deux, est explicable.
Reportant la valeur de ρ dans l’équation de Friedmann, on obtient l’équation : |
qui est à variables séparées, et s’intègre immédiatement. On en déduit le tableau des résultats, mis sous la même forme que précédemment :
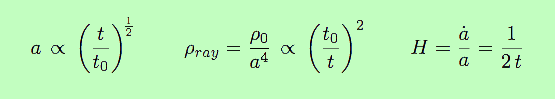
Remarque : ρ(t) a la même équation dans les deux cas, en 1 / t2.
Considérer ensemble la matière et le rayonnement rend le système d’équations beaucoup plus difficile à résoudre, bien que la solution exacte existe. La densité s’écrit comme la somme des densités de matière et de rayonnement : ρ = ρmat + ρray. Il n’y a cependant qu’une seule équation de Friedmann, qui fait intervenir la densité totale ρ. Pour obtenir des solutions simples, nous allons considérer que l’un des deux, matière ou rayonnement, domine l’autre. Le comportement du facteur d’échelle sera celui qui correspond au dominant, modifié d’une manière non significative par l’autre. Nous négligerons donc cette modification. Les équations pertinentes sont donc : ρmat ∝ 1 / a3 et ρrad ∝ 1 / a4.
Le rayonnement à dominé au début de l’Univers, lorsqu’il était très chaud. Nous avons vu que lorsque le rayonnement est seul, a(t) ∝ t1∕2. Il en sera approximativement de même ici, donc par substitution
![]()
![]()
Observant les puissances de t pour les densités de matière et de rayonnement, on remarque que la densité de matière diminue moins vite (puissance 3 ∕ 2 au dénominateur) que la densité de rayonnement (puissance 2). Ceci nous indique que, si le rayonnement est majoritaire au début, cette situation ne dure pas, car la densité de rayonnement baisse plus vite que celle de matière.
Cette simple constatation suffit pour comprendre que l’Univers à son début, très chaud, est dominé par le rayonnement, mais que par la suite, il sera dominé par la matière !
C’est le cas lorsque l’Univers s’est suffisamment étendu pour que la densité du rayonnement soit tombée bien en-dessous de celle de la matière, avant la formation des grandes structures. C’est aussi le cas après la formation des galaxies et des amas, car les interactions entre les galaxies sont très faibles. La pression est alors nulle. Lorsque la matière est dominante, on a : a(t) ∝ t2∕3. Reportant cette valeur dans les formules qui donnent les densités, on obtient :
![]()
![]()
On voit que la puissance qui gouverne la radiation est plus grande que celle qui gouverne la matière. Donc, là aussi, la radiation baisse plus vite que la matière. Nous avons supposé que la matière dominait dès le début ; cette domination s’amplifie donc au cours du temps. La domination de la matière est donc une situation stable, qui se renforce avec le temps.
Passons maintenant au cas où matière et rayonnement (ou matière relativiste) sont négligeables, mais dans lequel la constante cosmologique est non nulle. L’équation d’état liée à la constante cosmologique est p = -ρΛ c2. Le problème est donc :
| Equation de Friedmann | Equation du fluide | Equation d’état |
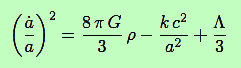 |
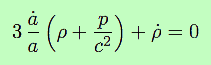 |
La valeur de cette constante peut être très faible. Que se passe-t-il dans ce cas ? Nous avons vu ci-dessus que la contribution de la matière donne une variation de ρ en 1 / a3, et la contribution de rayonnement (ou matière relativiste) une variation en 1 / a4, ce qu’on a résumé par ρmat ∝ 1 / a3 et ρrad ∝ 1 / a4. Partant d’un état dans lequel la constante cosmologique est très petite, mais non nulle, l’Univers va évoluer par expansion, de telle sorte que le premier terme de l’équation de Friedmann, proportionnel à ρ, va tendre vers 0 en 1 / a3 ou 1 / a4, et le terme de courbure est divisé par a2, donc tend vers 0 aussi. Par conséquent, les deux premiers termes seront négligeables au bout d’un certain temps. Par contre, la constante cosmologique, comme son nom l’indique, ne dépend pas de a, et sa valeur, même petite, deviendra forcément prépondérante au fil du temps.
Plaçons-nous donc dans cette perspective, où la constante cosmologique domine l’évolution de l’Univers. On considère donc que les deux premiers termes de l’équation de Friedmann sont nuls. Il reste :
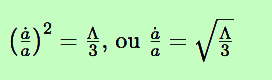
Λ doit être positive (elle est égale à un carré), donc elle contribue au taux d’expansion. Par conséquent, elle l’accélère.
C’est une équation à variables séparées, dont la solution s’obtient immédiatement :
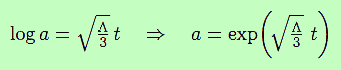
(On a pris la constante d’intégration nulle.
Le facteur d’échelle a est donc en croissance exponentielle a = ekt, en posant k égal à la racine carrée. C’est cette croissance qui représente l’inflation. On définit l’inflation comme toute époque pour laquelle le facteur d’échelle croît de plus en plus vite. Ceci signifie que la croissance s’accélère, et se traduit mathématiquement par la définition :
Même si la constante cosmologique est très petite, l’augmentation de a tend très rapidement vers l’infini.
Exemple de croissance exponentielle : la croissance économique.
Considérons une croissance de 10 % par an. La croissance exprimée en pourcentage est la variation du PIB par rapport au PIB lui-même. Le PIB p est analogue du facteur d’échelle a. Sa variation ![]() correspond à la variation du facteur d’échelle
correspond à la variation du facteur d’échelle ![]() . Et sa variation relative
. Et sa variation relative ![]() est analogue de
est analogue de ![]() . Dans les deux cas, la variation relative est constante. Donc les solutions sont analogues :
. Dans les deux cas, la variation relative est constante. Donc les solutions sont analogues :
![]() = 0,1 ⇒ p = exp(0,1 t) = e 0,1 t.
= 0,1 ⇒ p = exp(0,1 t) = e 0,1 t.
Au bout de 10 ans, p = 2,718 ; au bout de 20 ans, p = 7,38 ; au bout de 30 ans, p = 20 ; au bout de 40 ans, p = 55 ; au bout d’un siècle, p = 22.000…
Si vous avez placé 100 € en 1980 à 10 % (ou l’équivalent de 100 €…), vous aviez 272 € en 1990, 738 € en 2000, et 2.008 € en 2010. En 2080, vous totaliserez 22.026 €.
Naturellement, les ressources naturelles nécessaires pour assurer cette croissance sont exploitées au même niveau, alors que la planète est finie. Là où il y avait 100 voitures en 1980 (une file longue de 350 mètres, il y en aura 22.000 en 2080 (une file de 77 kilomètres)…
Reprenant alors l’équation de l’accélération :
![]()
a étant toujours positif, le terme ä ∕ a est positif. Donc, le membre de droite doit l’être aussi. Puisqu’il est précédé du signe moins, et que les constantes devant la parenthèse sont positives, il faut que le terme entre parenthèses soit négatif :
![]()
La pression doit être négative ! Comment peut-on imaginer une pression négative ? La pression est la force appliquée par unité de surface. Mais on n’a jamais considéré qu’une force qui pousse… Si on envisage une force qui tire, elle est dans l’autre sens, donc négative. Une pression négative peut donc s’envisager.
L’inflation débute lorsque la constante cosmologique prend le dessus sur les deux autres termes dans l’équation de Friedmann. Elle produit une croissance exponentielle de l’Univers, de plus en plus rapide. Si elle avait duré jusqu’à maintenant, l’Univers serait infiniment plus dilué qu’il n’est. Ce qui prouve que l’inflation s’est arrêtée, et nous pose la question de savoir pourquoi et comment (tout comme se pose la question de savoir pourquoi et comment elle a débuté).
L’inflation est une solution mathématique aux deux problèmes de la courbure et de l’horizon. En ce sens, elle est déjà intéressante. Elle est autorisée par les équations, mais pas obligatoire. Ceci lui donne donc un certain aspect ad-hoc. L’idéal serait de lui trouver maintenant une solide justification physique, qui la rendrait naturelle.
L’inflation étant définie par ä > 0, l’inflation provient de la constante cosmologique. Mais celle-ci n’a pas, pour l’instant, de justification physique. Historiquement, Einstein l’a introduite pour de mauvaises raisons, qu’il a regrettées par la suite : elle lui a permis de stabiliser artificiellement (et provisoirement) un Univers qui ne demande qu’à bouger. Plusieurs idées se font jour maintenant pour l’interpréter.
Tout d’abord, la valeur de la constante cosmologique doit varier ! Elle n’est constante que dans certaines tranches de temps bien définies… Cette variation permet de faire démarrer, puis d’arrêter l’inflation. Il nous faut donc trouver une interprétation qui provoque ces variations. Plusieurs voies s’ouvrent par des perspectives de physique théorique, mais cette physique n’est pas encore validée par les expériences, qui n’atteignent pas les niveaux d’énergie nécessaires. Aussi, les explications que l’on peut proposer restent encore spéculatives, mais sont des axes de recherche intéressants.
Une telle situation entraîne donc une augmentation des distances extrêmement rapide, beaucoup plus rapide que l’expansion normale. C’est cette propriété de l’inflation qui va permettre de résoudre plusieurs problèmes que pose le modèle standard cosmologique.
Pour résumer :
| domination du rayonnement | a ∝ ( t / t0)1/2 |
| domination de la matière | a ∝ ( t / t0)2/3 |
| domination de la constante cosmologique | a = exp(k t) |
La constante cosmologique a donc un effet semblable, mais opposé, à celui de la matière (qui relentit l’expansion alors que la constante cosmologique l’accélère). Il apparaît donc naturel, pour définir sa contribution, de lui faire correspondre un rapport ΩΛ à la densité critique. Pour cela, considérons que la densité ρ et la courbure k sont nulles. Dans l’équation de Friedmann, il ne reste que H2 = Λ / 3, c’est-à-dire Λ / 3 H2 = 1. Si donc, la constante cosmologique était seule en cause, la densité de l’Univers serait critique, et s’exprimerait par cette valeur. On pose donc par définition ΩΛ = Λ / 3 H2. Faisant de même pour le terme de courbure, l’équation de Friedmann se réduit à H2 = k / a2 ; d’où l’on tire : k / a2 H2 = 1. On en déduit la définition du rapport Ωk = - k / a2 H2.
En reprenant la valeur de Ω, on obtient successivement : Ω = ρ / ρc où ρc = 3 H2 / 8 π G ; donc ρ = 3 H2 / 8 π G Ω ;
et en reportant ces valeurs dans l’équation de Friedmann, il vient :
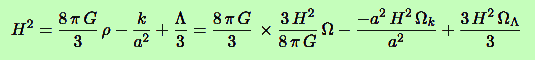
H2 = H2 Ω + H2 Ωk + H2 ΩΛ
et l’équation de Friedmann donne tout simplement :
Ω + Ωk + ΩΛ = 1
On parle d’histoire thermique parce que la température est décroissante au cours du temps, et qu’elle détermine les phénomènes physiques successifs qui peuvent se dérouler à chaque instant. Dans cette optique, la température est équivalente au temps.
Le début de l’Univers a été nommé Big Bang par Fred Hoyle et par dérision ! Fred Hoyle était partisan de la création continue, qui explique que les vides créés par l’expansion sont comblés par une création de matière, qui se produit en permanence. Il n’est pas nécessaire d’en créer beaucoup pour cela : le calcul donné plus haut de la vitesse d’expansion montre qu’un atome d’hydrogène par année-lumière, de temps en temps, suffit amplement. Mais cette théorie n’a pas un support observationnel suffisant, et elle est abandonnée par l’immense majorité des chercheurs. Mais Fred Hoyle, au cours d’une émission de radio et voulant se moquer de Georges Lemaître créateur de la théorie concurrente, a inventé le terme de Big Bang qui a fait florès.
Nous allons donc décrire ce qui s’est passé, si la théorie fondée sur le Big Bang est correcte, au moins en grande partie. Et le tout début pose déjà problème : en effet, la densité et la température de l’Univers étaient alors si élevées, que la physique que nous connaissons ne peut pas suivre. Nos connaissances proviennent d’expériences faites dans les grands accélérateurs de particules, le LHC atteignant aujourd’hui les 7 TeV (il doit passer à 14 TeV bientôt). Ceci correspond à une température de l’ordre de 8 1016 K soit 80 millions de milliards de degrés ! C’est une température impressionnante, mais tout de même, en remontant le temps, elle a dû être dépassée. On ne peut pas faire d’expériences, à l’heure actuelle, à des températures plus élevées. On est donc incapable de dire ce que pouvait être l’état de l’Univers lorsque sa température était plus élevée que cette limite.
| événement | énergie | température | z | date |
|---|---|---|---|---|
| ère de Planck | 0 | |||
| temps de Planck | 1028 eV | 1032 K | 1032 | 10-43 s |
| transition de phase Grande Unification | 1023 eV | 1027 K | 1027 | 10-35 s |
| transition rayonnement-matière | ||||
| quarks | 1021 | 1025 | 1015 | 10-11 s |
| baryogénèse | > 109 | 12.000 milliards de K | < 4 10-6 s | |
| formation des hadrons (transition QCD) | 4 108 eV | 4.640 milliards de K | 4 10-6 s | |
| annihilation des électrons | 106 eV | 11,6 milliards de K | 1010 | 1 s |
| nucléosynthèse | 6 104 eV | 0,69 milliards de K | 105 | 3 min |
| prépondérance de la matière | 0,8 eV | 9.280 K | 50.000 ans | |
| recombinaison | 0,26 eV | 3.000 K | 1.100 | 500.000 ans |
| découplage | 1.100 | en fin de recombinsaison | ||
| formation des structures | 10-3 eV | 12 K | 10 ? | 1 milliard d’années |
| aujourd’hui | 2,349 10-4 eV | 2,725 K | 0 | 13,7 milliards d’années |
La première ligne, grisée, indique que la physique nécessaire pour décrire l’Univers est encore inconnue.
A partir de l’hypothétique Big Bang, l’expansion commence, et la température baisse, à partir d’une valeur éventuellement infinie, pour atteindre sa valeur actuelle. Pour expliquer l’évolution de l’Univers, nous avons recours à des expériences qui nous permettent de reproduire en laboratoire des conditions proches de celles qui régnaient à certaine époque dans l’Univers. Mais nos expériences sont limitées, et ne peuvent prétendre atteindre les conditions initiales. Relativement à nos moyens physiques, nous pouvons diviser l’histoire thermique de l’Univers en trois époques :
Les théories supersymétriques supposent, et posent donc comme principe fondateur, que chaque boson possède un fermion associé et réciproquement. On dit que ce sont des partenaires supersymétriques. Elles englobent le modèle standard, dont elles reprennent donc les résultats, mais vont plus loin. Les partenaires supersymétriques des particules connues ne sont pas des particules connues, c’est un premier résultat de ces théories. Il faudrait donc découvrir de nombreuses particules nouvelles, ce qui n’a pas été le cas jusqu’à présent. Ceci, soit parce que ces particules n’existent pas -la théorie étant basée sur un mauvais principe-, soit parce que ces particules sont trop massives pour que les accélérateurs utilisés jusqu’à maintenant aient pu les mettre en évidence. Beaucoup de physiciens penchent pour cette seconde hypothèse, mais ceci ne suffit pas pour valider la théorie ! Ces théories sont spéculatives.
Même si les théories supersymétriques sont invalidées par des expériences futures, les physiciens gardent une bonne confiance dans l’unification des forces, qui s’esquisse dans les résultats actuels.
Les caractéristiques globales de l’Univers qui se conservent sont : la charge électrique, la charge leptonique, et la charge baryonique. La charge électrique globale était nulle, puisqu’elle se conserve, et qu’elle est nulle aujourd’hui. La charge leptonique est la différence entre le nombre de leptons et le nombre d’anti-leptons. Il en est de même de la charge baryonique. Ces particules se créant par paires, ces deux charges sont également nulles. Toutefois, il est possible que les particules et les antiparticules correspondantes n’aient pas exactement la même probabilité de se désintégrer (se désintégrer signifie se transformer en d’autres particules, ne pas confondre avec l’annihilation particule-antiparticule). Si ces probabilités diffèrent, il y aura un excès de la particule (resp. antiparticule) si elle se désintègre moins facilement que l’antiparticule (resp. particule).
Immédiatement après le Big Bang, si celui-ci a un sens, la densité est telle que la gravitation est très forte, et la description de l’Univers ne pourrait se faire qu’à l’aide d’une théorie quantique ET relativiste, qui n’existe pas encore. Avant le temps de Planck, soit 10-43 s, c’est donc l’inconnu.
Les théories spéculatives actuelles prévoient que toutes les interactions s’unifient (Théorie de Grande Unification). Elles ont donc la même intensité (l’interaction faible ne mérite plus son nom…). La gravitation, si faible actuellement, aurait pu être de même intensité que l’interaction électromagnétique. En ces temps reculés (une infime fraction de seconde après la singularité), l’Univers observable (ce qualificatif n’ayant alors guère de sens) était de l’ordre de grandeur de la taille d’une particule…
A ce niveau de température, l’énergie suffisante pour créer des paires particule-antiparticule est disponible. Même le champ gravitationnel intense aurait pu en engendrer. De très nombreuses particules diverses (électrons, muons, quarks, divers hadrons, divers mésons…) peuvent être créées ainsi, leur masse le permet. Mais les hadrons et les mésons sont formés de quarks. Et les quarks ont la propriété de liberté asymptotique, c’est-à-dire que plus ils sont proches, plus faible est la force les liant. Dans les conditions de densité qui nous intéressent, les quarks sont extrêmement compressés, et par conséquent libres. Donc les hadrons et mésons ne peuvent être stables, et le contenu de l’Univers est constitué uniquement de photons, de leptons (électrons, muons, neutrinos, et leurs antiparticules), et de quarks.
Actuellement, les neutrinos interagissent très peu avec les autres particules. La moitié d’un flux de neutrinos pourrait ressortir après avoir traversé une année-lumière de plomb ! Mais dans les conditions de l’immédiat après Big Bang, la densité est telle que même les neutrinos interagissent énormément avec les autres particules. On est donc en présence d’une relation d’équilibre thermique : toutes les particules sont à la même température, ce qui signifie qu’elle vont toutes à la même vitesse moyenne. A ce niveau d’énergie, elles sont bien sûr relativistes, et se comportent comme un rayonnement.
Il se crée en permanence des paires, et toutes les particules interagissent, se désintègrent éventuellement, et s’annihilent.
Un peu plus tard, à une énergie de 1024 eV (1028 K), la gravitation se découple des autres interactions. On le sait par l’extrapolation des courbes connues actuellement, qui montrent que les forces doivent s’équilibrer à ce niveau d’énergie. Son intensité va diminuer au fil de l’expansion, pour arriver aujourd’hui à un niveau extrêmement bas par rapport aux autres interractions.
Les forces forte, faible et électromagnétique sont encore unifiées. Elles se séparent à une énergie d’une centaine de GeV, accessibles à nos instruments.
Le décrochage de la gravitation des quatre autres interactions, avec la baisse de température, est analogue d’un gel : avant, il y avait une grande symétrie entre les particules ; un grand désordre règne. Après, un état plus lisse, plus ordonné le remplace. Dans le gel de l’eau en glace, les molécules d’eau (qui ne sont pas symétriques) sont libres de prendre n’importe quelle position et n’importe quelle orientation avant, puis sont figées dans un réseau cristallin orienté après. Peut-être s’est-il passé quelque chose de ce genre, si ces théories sont représentatives, et si rien n’a empêché d’atteindre de telles densités et températures.
Lorsque la température de l’Univers était de plusieurs dizaines de milliards de degrés, les chocs entre nucléons auraient été tellement violents, qu’ils n’auraient pu être stables. La théorie des particules élémentaires nous indique que l’Univers devait donc être rempli d’un plasma quarks-gluons : les quarks sont les constituants des nucléons, dans lesquels ils sont confinés par l’interaction forte ; les particules médiatrices de cette interaction sont les gluons.
Lorsque la densité augmente fortement, les quarks sont forcés de se rapprocher. Or l’interaction forte entre deux quarks est d’autant plus forte qu’ils sont plus éloignés (contrairement au comportement des autres forces, qui faiblissent avec la distance croissante). Donc, lorsque les quarks se rapprochent, ils gagnent en liberté. On parle de liberté asymptotique. Les quarks qui constituent les nucléons ne sont plus liés, les nucléons n’ont donc plus d’existence propre. Les gluons qui collaient les quarks sont eux-mêmes libres, et l’ensemble forme un plasma quarks-gluons.
La preuve expérimentale d’existence de ce plasma est récente. La première a été réalisée au CERN en février 2000, avec des noyaux de plomb accélérés à 33 TeV, soit une température de l’ordre de 1.500 milliards de degrés. Depuis, l’expérience a été refaite aux Etats-Unis, et maintenant au CERN à nouveau, avec des noyaux de plomb à haute énergie (5 GeV fm-3, alors que le seuil est de 3 GeV fm-3).
La preuve expérimentale est donnée par deux événements permettant de tracer la création du plasma. Lorsque les quarks sont ainsi libres, les c et c’ ne forment plus le J / Ψ, mais restent séparés. L’absence de J / Ψ est donc un signe de la formation du plasma, et a été observée dans les collisions réalisées au CERN. D’autre part, lorsque le plasma se détend, sa densité baisse, et les quarks s’éloignent et perdent leur liberté. Ils sont alors obligés de se regrouper pour former des hadrons. Or l’énergie disponible avant la détente a permis la formation de quarks lourds, les quarks étranges (s). On devrait donc observer la formation de hadrons étranges, combinaisons de ces quarks. L’expérience WA97 a ainsi mis en évidence un taux multiplié par 50 de la production des particules Ω (formées de trois quarks sans u ni d), et de leurs antiparticules Ω’ (formées des antiquarks correspondants).
Pendant les quelques 20 à 30 micro-secondes qui suivirent le Big Bang, l’Univers devait donc être formé de ce plasma quarks-gluons. A ce stade, il ne contient, outre les quarks et gluons, que des leptons (électrons et positrons, neutrinos et anti-neutrinos), et bien sûr des photons. Les particules composites (nucléons, mésons…) ne peuvent se former, car l’énergie disponible est supérieure à l’énergie de liaison de leurs constituants. De plus, toutes ces particules sont en équilibre thermique. L’équilibre thermique est réalisé lorsque toutes les particules ont la même vitesse moyenne. Pour cela, il faut que leurs interactions soient très fréquentes, pour qu’elles échangent de l’énergie cinétique.
On sait que les neutrinos interagissent extrêmement peu avec les autres particules. Mais à cette époque, la densité était tellement élevée, que même les neutrinos subissaient d’incessantes collisions, qui égalisaient leur énergie avec celle des particules qu’ils rencontraient. Ainsi, l’équilibre thermique était réalisé entre toutes les espèces de particules. Une seule température était suffisante pour décrire l’Univers.
Pour se faire une idée un peu plus précise de ce que pouvait être l’Univers dans ces conditions, on peut regarder une photo prise à l’aide d’un accélérateur de particules.
Cette image peut donner une idée de ce que doit être le plasma quarks-gluons. Ici, deux particules se sont heurtées, et ont donné naissance à toutes les autres. Les trajectoires courbées indiquent la charge électrique des particules, déviées dans le champ magnétique de l’instrument. Dans l’Univers primordial, ce genre d’événement devait se produire à tout instant et en tout lieu…
Cet équilibre thermique a une conséquence importante : il a effacé toutes les propriétés antérieures de l’Univers. Ce qui nous permet de parler de la suite avec assez d’assurance, même dans l’ignorance où nous sommes des premiers instants de l’Univers ! Cet équilibre ne pouvait durer. Avec l’expansion, la densité chutait rapidement, et elle s’est trouvée bientôt trop faible pour maintenir un taux élevé de collisions des neutrinos. Alors, ceux-ci se sont découplés des autres particules (photons compris), à la température courante du milieu, et ont commencé à se refroidir en fonction de l’expansion. Par découplage, on entend que les interactions entre ces deux types de particules cessent, et donc que les vitesses moyennes de chaque classe deviennent indépendantes. Par conséquent, leurs températures peuvent se différencier.
Les neutrinos se sont découplés lorsque la température est tombé en-dessous de 4 MeV, soit en-dessous de 50 milliards de degrés Kelvin (1 eV correspond à 11.600 K, donc T = 11.600 × 4 106 K = 46,4 109 K). Ceci s’est passé au temps t = (1 MeV / T)2 s = (1 MeV / 4 MeV)2 s = 0,625 s
Les neutrinos ont alors pris leur indépendance, conservant leur profil d’équilibre thermique, et se refroidissant en fonction de l’expansion. Nous verrons que les photons ont été réchauffés par la suite. Mais les neutrinos n’en ont pas profité. Aussi, leur température aujourd’hui est-elle plus basse que celle des photons, dans un rapport 0,71, ce qui fait Tν = 2,725 × 0,71 = 1,934 K.
Les neutrinos primordiaux constituent donc un fond cosmologique de même nature que les photons. Mais étant donné la faible probabilité d’interaction des neutrinos, et leur basse température, il faudra améliorer fortement nos moyens de détections si on veut un jour les observer. Leur observation sera donc l’un des grands enjeux de la cosmologie future.
La température est suffisamment descendue pour que les quarks commencent à ressentir l’interaction forte, puisque la densité plus faible leur permet de s’éloigner un peu. Protons et neutrons se forment donc, ainsi que leurs antiparticules antineutrons et antiprotons. Aussitôt, lorsque des protons rencontrent des antiprotons, les paires commencent à s’annihiler, mais ceci n’est pas instantané. Il s’établit donc une réaction d’équilibre, qui permet de maintenir une proportion de ces particules.
A ce stade, l’Univers contient des neutrons, antineutrons, protons, antiprotons, électrons positrons, neutrinos et antineutrinos. Toutes ces particules sont libres, car l’énergie encore disponible ne leur permet pas de s’assembler.
Lorsque la température est tombé en-dessous de l’énergie suffisante pour créer des paires proton-antiproton et neutron-antineutron, cette création cesse. Et l’annihilation continue… Puisque ces particules se sont formées pas paires, on penserait qu’il y en ait exactement le même nombre : autant de protons que d’antiprotons, et ils devraient s’anihiler en totalité ; l’Univers serait vide… Mais une légère brisure de symétrie (différence entre le nombre de protons et le nombre d’anti-protons à leur formation) permet à un proton sur un milliard de subsister.
Ce phénomène de brisure de symétrie n’est pas totalement compris actuellement, et les recherches continuent pour lui trouver une explication vraiment satisfaisante.
On passe maintenant en-dessous de la température (énergie) nécessaire pour créer des paires électron-positron. La création est en panne, mais l’annihilation continue. Puisqu’à chaque électron créé correspond un positron, il y a le même nombre de chaque. Ce qui veut dire qu’ils vont maintenant se retrouver et s’annihiler. Il ne devrait donc plus rester le moindre électron…
Pourtant, on en observe aujourd’hui. Pour jusitifer cette présence, il faut considérer que l’annihilation n’a pas été parfaite. Mais s’il avait subsité autant de positrons que d’électrons, on verrait aujourd’hui encore des annihilation, qui s’accompagneraient d’émission de lumière (deux fois l’énergie de masse de l’électron). Et ce n’est pas le cas. Donc il ne reste plus aujourd’hui que des électrons, et point de positrons. Il faut admettre qu’il y a eu là aussi une brisure de symétrie, phénomène qui a favorisé les électrons par rapport à leurs antiparticules. Le calcul montre qu’il suffit d’une disymétrie de 10-9 pour assurer la quantité d’électrons observés actuellement. Il faut dire qu’au début de l’expansion, l’énergie était telle qu’une quantité énorme de paires électron-positron a été créée. Autant que de photons.
Et aujourd’hui, il reste exactement autant d’électrons que de protons, puisque l’Univers est globalement neutre. Si ce n’était pas le cas, l’Univers aurait une charge électrique, positive si les protons l’emportaient numériquement sur les électrons, négatives dans le cas contraire.
Un petit calcul très simple est édifiant. Considérons la quantité de lumière émise par une galaxie ; elle correspond à l’énergie produite par fusion de l‘hélium (les autres fusions sont moins énergétiques, et durent bien moins longtemps, donc sont négligeables). Supposons que les étoiles de cette galaxie existent toutes depuis l’origine de l’Univers, soit 10 milliards d’années. Calculons combien d’hélium elles ont produit :
La masse typique d’une galaxie est de l’ordre de 3 1041 kg. Donc la masse d’hélium produite par les étoiles ne représente que la fraction 2 1039 kg / 3 1041 kg, soit à peu près 1 % de la masse de la galaxie. Ceci ne peut en aucun cas justifier les 24 % observés, d’autant plus que l’hélium produit reste confiné à l’intérieur de l’étoile, sauf si celle-ci explose, ce qui n’est le cas que pour les plus massives, donc une faible proportion d’entre elles. Ceci diminue d’autant la quantité d’hélium stellaire présente dans l’Univers.
Un argument supplémentaire s’ajoute : si l’hélium observable dans l’Univers provenait des étoiles, il s’accompagnerait d’autres éléments, produits aussi en abondance. La proportion de carbone et d’oxygène, éléments les plus légers produits par les étoiles après l’hélium, serait bien plus forte que ce qui est observé. Donc, l’hélium présent actuellement dans l’Univers ne provient que pour une infime partie de la fusion stellaire.
Il faut donc invoquer un autre mécanisme pour expliquer l’abondance d’hélium. Revenant aux observations, on peut aussi constater que la proportion d’hélium est pratiquement la même dans les objets très vieux (amas globulaires) et jeunes. Donc, l’hélium est présent depuis la formation de l’Univers, il est primordial en très grande partie.
Le modèle du Big Bang chaud permet d’expliquer cela. En effet, l’Univers était très chaud et dense au début, ce qui représente des conditions proches de celles que l’on rencontre aujourd’hui au cœur des étoiles. Les mêmes causes produisant les mêmes effets, la fusion de l’hydrogène s’y est réalisée pareillement.
Georges Gamow a pensé qu’avec le refroidissement, les protons ont capturé des neutrons, et que certains de ces derniers, par décroissance béta, se sont transformés en protons. Il croyait expliquer ainsi tout ce qu’on voit aujourd’hui.
Mais ceci ne peut pas se produire, tout simplement parce que la température a baissé trop vite. Après formation de l’hélium, et d’un peu de lithium, il ne restait plus assez d’énergie pour former les éléments plus lourds.
La température de l’Univers n’a fait que décroître. Lorsqu’elle était très élevée, il n’y avait que de l’hydrogène, rien d’autre à fusionner. Il a fallu attendre que la température baisse suffisamment pour former de l’hélium. Lorsque celui-ci a été présent, la température était devenue trop basse pour qu’il fusionne à son tour… C’est pourquoi l’Univers primordial ne pouvait contenir que de l’hydrogène, une proportion forte (1/4) d’hélium, et des traces de lithium, de deutérium.
Il a fallu trouver un autre (ou plusieurs) mécanisme(s) pour expliquer tout ce qui est plus lourd que le lithium, c’est-à-dire la quasi-totalité des éléments chimiques naturels.
Dans une étoile, les conditions sont stables. Le milieu est en équilibre. Par contre, l’Univers primordial était en expansion rapide, et par conséquent les conditions thermodynamiques y changeaient rapidement. Il a été d’abord si chaud que le rayonnement de corps noir qu’il produisait détruisait tout atome composé qui aurait tenté de se former. Impossible d’avoir quoi que ce soit d’autre que de l’hydrogène (proton seul). Puis, la température a baissé, et les photons étaient donc un peu moins énergétiques. Jusqu’à ce qu’ils ne le soient plus assez pour briser un atome d’hélium. Ceux-ci se formaient toujours, mais n’étaient plus détruits. Donc ils commençaient à s’accumuler. Jusqu’à quand ?
La température baisse toujours. On sait bien que dans les étoiles, elle doit être au-dessus de 10 millions de degrés pour permettre la fusion de l’hydrogène. Donc, lorsque la température est tombée en-dessous de cette valeur approximative, la fusion de l’hydrogène en hélium s’est achevée, et le taux d’hélium produit s’est donc figé.
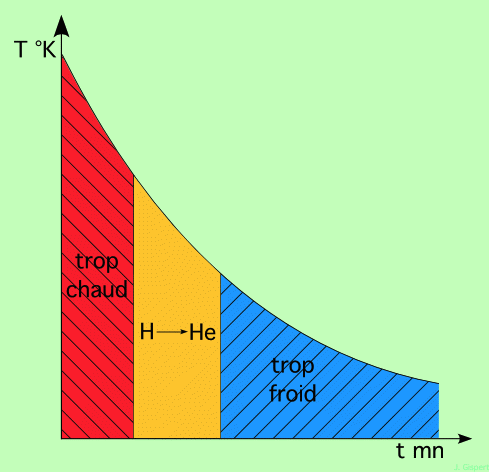
La figure 1.1 représente la baisse de température T en fonction du temps t. Dans la partie en rouge, l’Univers était trop chaud, les photons trop énergétiques, et les noyaux juste formés étaient immédiatement brisés. Dans la partie jaune, le taux de destruction baisse, et donc de plus en plus de noyaux subsistent. Enfin, dans la partie bleue, il faut trop froid pour autoriser la fusion, et donc la création s’arrête.
Par conséquent, la phase de production de l’hélium (et avec lui d’un peu de deutérium, de lithium et d’hélium 3) n’a duré que peu de temps, et cette durée correspond à la proportion de ces éléments que l’on observe aujourd’hui. Par conséquent, ces proportions nous donnent un critère important pour déterminer pendant combien de temps la température est resté dans la fourchette permettant une production d’hélium. On estime que la nucléosynthèse s’est terminée 100 s après le Big Bang.
L’excellente identité entre le taux calculé et le taux mesuré est un des grands arguments en faveur des théories de Big Bang.
La densité de l’univers était telle, jusqu’à cette étape, que le rayonnement et la matière étaient en équilibre thermique. Les particules de matière elles-mêmes étaient tellement énergétiques (vitesses relativistes), que leur onde quantique était prépondérante, et qu’elles se comportaient comme un véritable rayonnement. Cette période de l’Univers est nommée ère du rayonnement. Elle a pris fin lorsque les électrons ont été désactivés en s’associant avec les protons. Ceci les a privés de leurs interactions avec les photons, et a donc rompu le mécanisme d’équilibrage thermique.
Après la nucléosynthèse, les noyaux atomiques existaient, mais les électrons ne leur étaient pas liés, la température étant trop forte. Dès qu’une capture avait lieu, un photon ou un choc venait fournir l’énergie d’ionisation, et l’électron était libéré. Donc, la matière était totalement ionisée. Ceci jusqu’au moment où la température est tombé assez bas pour ne plus pouvoir ioniser les atomes. On peut définir le temps de survie d’un électron lié à un noyau. Ce temps de survie était très bref à haute température, mais avec la baisse de température il augmentait progressivement.
Le nombre d’atomes neutres (ayant leur cortège électronique), partant de 0 %, a donc monté progressivement, pour atteindre presque 100 % lorsque la température a été assez basse. Cette capture des électrons par les noyaux est nommée recombinaison, terme particulièrement mal adapté puisqu’avant, électrons et noyaux n’avaient jamais été couplés, la température étant bien trop haute pour cela. Mais le terme est consacré… L’association des électrons négatifs avec les noyaux positifs forme des atomes neutres.
La recombinaison n’a pas été instantanée.
Considérons le même phénomène, mais en s’intéressant maintenant à la lumière. Avant la recombinaison, les photons se déplacent dans un milieu constitué d’un gaz de noyaux et d’électrons. Tous les électrons sont libres, et exercent pleinement leur champ électromagnétique. Tout photon qui passe à proximité d’un électron est diffusé par diffusion Thomson. Il change donc de trajectoire, et reste piégé dans le gaz. Sur sa nouvelle trajectoire, il ne tarde pas à rencontrer un autre électron, qui le diffuse à nouveau. Par conséquent, le libre parcours moyen du photon (longueur du trajet qu’il peut accomplir en ligne droite entre deux diffusions successives), est très court. Ils tournent en rond. Mais à mesure que les électrons sont capturés par les noyaux, leur influence électrique est neutralisée par celle, de signe opposé, du noyau, et l’électron n’agit plus sur les photons. Les photons ont de plus en plus de chances de passer, donc leur libre parcours moyen augmente, tout en restant fini.
Lorsqu’il ne reste pratiquement plus d’électrons libres, le libre parcours moyen des photons devient infini. Cette libération des photons est nommée découplage.
Ceci se produit lorsque la température est de l’ordre de 3.000 K, au même moment (dans le temps cosmique) partout dans l’Univers. Donc, vu de la Terre, tous ces photons viennent de la même distance, et tous les points d’émission que nous voyons aujourd’hui forment donc une sphère centrée sur nous. Bien sûr, il ne s’agit que d’une apparence, qui serait identique vue d’une autre galaxie. Cette sphère est nommée surface de dernière diffusion, nom qui apparaît naturel au vu des explications qui précèdent.
Le décalage spectral, au moment du découplage, est de l’ordre de z = 1.100.
L’histoire ci-dessus montre que la recombinaison précède juste le découplage, qui se produit lorsqu’elle se termine, quelques 380.000 ans après le Big Bang.
Après le découplage, les photons peuvent enfin parcourir l’Univers. Mais ce voyage va être long ! Plus de dix milliards d’années… Et pendant ce temps, l’Univers est en expansion, donc les longueurs augmentent entre deux points quelconques. Par conséquent, les longueurs d’onde aussi : elles ont été multipliées par 1.100. C’est pourquoi nous observons aujourd’hui ce rayonnement à une grande longueur d’onde, correspondant à une température de seulement 2,725 K (3.000 K / 1.100 = 2,727 K). Evidemment, la surface de dernière diffusion est celle qu’on voit en observant le fond diffus cosmologique !
Une conséquence importante du découplage est qu’il a mis fin à l’équilibre thermique entre la matière et les photons. Cet équilibre était produit par les incessantes interactions entre les deux ; mais puisque les interactions cessent, il n’y aura plus d’équilibre, et matière et rayonnements vont pouvoir évoluer indépendamment l’un de l’autre.
Les infimes fluctuations de température que l’on voit aujourd’hui dans le rayonnement cosmologique montrent des différences de densité correspondantes. Par conséquent, ces zones sont gravitationellement un peu plus attractives que les zones voisines. Donc, elle vont croître. Et plus elles croissent, plus elles attirent… Un mécanisme d’effondrement est donc à l’œuvre, qui va donner les galaxies et les amas. Cette formation est traitée ans le chapitre sur les galaxies.
Après la recombinaison, l’Univers était transparent, les photons le traversaient sans interactions. Mais rien ne produisait plus de nouveaux photons. Avec l’expansion, les longueurs d’ondes augmentaient comme le facteur d’échelle, et donc produisaient un déclage vers le rouge. Dans ces conditions, la lumière ambiante rougissait de plus en plus, pour finalement passer dans l’infrarouge. A ce moment-là, l’Univers est devenu noir ! Le ciel ne brillait absolument plus, puisqu’aucun photon visible n’était plus produit, et que les photons de la recombinaison étaient devenus infrarouges. C’est pour cette raison que l’on appelle cette période les âges sombres.
Aujourd’hui, le ciel nocturne est toujours noir, mais le Soleil et les étoiles nous montrent bien qu’il existe des sources de lumière visible. Donc, les âges sombres ont pris fin. Quand ?
Pour terminer cette période, il faut une source de photons visibles. Après la recombinaison, l’Univers était rempli des éléments produits pendant la nucléosynthèse, hydrogène, hélium, un peu de deutérium, de lithium, d’hélium 3. Que pouvaient devenir ces nuages ? Soit ils restaient tels, auquel cas l’Univers serait encore aujourd’hui dans cet état, soit ils devaient se condenser pour former des objets plus denses. C’est bien sûr cette seconde possibilité qui a été en œuvre, et qui a donné les premières étoiles. Pour en arriver là, il faut qu’il y ait dans l’Univers après la recombinaison de petites fluctuations de densité, suffisantes pour produire des germes de condensation. Un tel germe devenant plus dense, produit une gravité plus importante, et donc attire encore plus la matière environnante. Ce qui fait grossir le germe, et augmente sa gravité.
Lorsque ce mécanisme a réussi à condenser une étoile, qui s’allume, des photons sont produits, et l’Univers s’illumine à nouveau.
Les étoiles qui viennent de se former sont de métallicité nulle, puisque la nucléosynthèse n’a produit aucun élément plus lourd que le lithium. Or la théorie des étoiles indique que leur masse maximale est fonction de la métallicité : plus faible est la métallicité, plus massive sont les étoiles. Par conséquent, de nombreuses étoiles massives ont dû se former à peu près au même moment.
Or les étoiles massives, pour maintenir leur équilibre, doivent produire énormément d’énergie, et par conséquent être très chaudes. Par suite, elles émettent beaucoup de photons de grande énergie, ultraviolets. Ces photons étaient suffisamment énergétiques pour ioniser tout atome qu’ils rencontraient. Ce qui fait que l’Univers, ionisé après le Big Bang, puis devenu neutre par manque d’énergie, se retrouve ionisé par l’action des premières étoiles.
La date de cette réionisation est très incertaine. Elle est notée par le décalage spectral correspondant, qui est estimé entre 6 et 16. Une belle marge… Cette incertitude est liée, évidemment, à celle qui pèse sur l’âge des premières étoiles, que l’on n’a pas encore observées.
Quelle est la matière noire ? Elle est détectée par ses effets gravitationnels seulement, donc elle n’interagit pas avec la lumière. Mais il y a plusieurs explications possibles :
Naines brunes Ce sont des étoiles de très faible masse, trop faible pour assurer la fusion de l’hydrogène, mais assez pour entraîner celle du deutérium (l’isotope de l’hydrogène qui est produit par la première réaction dans la fusion de l’hydrogène normale). Leur faible masse leur confère un petit diamètre (un peu plus de 100.000 km, soit un peu plus gros que Jupiter). Elles ne rayonnent que par leur énergie gravitationnelle de formation, se refroidissant sans cesse. Leur très faible éclat les rend très difficiles à imager, et la première n’a été découverte qu’à la fin des années 90. Leur masse relativement grande et leur discrétion en font des candidats envisageables pour la matière noire.
Naines blanches Les naines blanches sont les restes d’étoiles de faible masse, après la fin de la fusion (de l’hydrogène pour les moins massives, de l’hélium pour les autres). Très condensées, elles sont de faible diamètre (10.000 km pour une masse solaire). Comme le rayonnement émis est proportionnel à la surface émissive, elles rayonnent très peu, donc sont d’éclat si faible qu’elles sont très difficiles à voir. D’autre part, toujours à cause de cette petite surface, elles n’arrêtent pas la lumière des astres situés derrière. Elles restent donc invisibles, et peuvent contribuer à cette masse inconnue.
Etoiles à neutrons La situation est très semblable à celle des naines blanches, avec une concentration encore plus grande de la matière (pour une masse solaire, le diamètre se réduit à 10 km). Bon candidat potentiel donc.
WIPMS Ce joli sigle vient de l’anglais Weakly Interactive Massive Particules. On considère qu’il puisse exister des particules massives (pour expliquer la gravité), mais qui n’interagissent que gravitationnellement (pour expliquer qu’elles ne soient pas détectées).
La recherche de ces objets a été tentée par divers moyens. Pour les objets compacts, nous avons constaté qu’ils étaient invisibles, au sens propre. Il faut donc trouver un moyen de les détecter indirectement. Ce moyen nous est donné par la Relativité Générale, avec le phénomène de lentille gravitationnelle. Lorsqu’un objet compact passe devant un objet brillant, il dévie sa lumière autour de lui, et la concentre un peu comme le ferait une lentille optique. L’objet apparaît donc un peu plus brillant. Si on est capable de mesurer cette augmentation d’éclat, on pourra en déduire que quelque chose l’a produite. Il restera à éliminer d’autres causes, et pour cela la durée du phénomène et la forme de la courbe de lumière sont déterminants. Des satellites ont été expédiés dans l’espace pour réaliser ce programme de recherche. Les deux plus importants ont été EROS (Expérience de Recherche d’Objets Sombres) et MACHO (Massive Compact Halo Objects). Ces deux sondes ont trouvé des objets, mais en très petit nombre. Aussi, la matière sombre ne peut être composée d’objets compacts que dans la limite de 15 % au maximum. La chasse au reste est toujours ouverte…
Une autre idée concerne des nuages d’hydrogène qui seraient invisibles même en raie à 21 cm (transition de spin). De tels nuages devraient se trouver loin de toute source d’énergie, sinon ils seraient visibles par les moyens traditionnels. Toutefois, la théorie de la nucléosynthèse primordiale met une barrière à la quantité de matière normale qui pourrait ainsi nous échapper. La solution correspondante ne peut être que vraiment partielle, il faut encore chercher ailleurs.
Les WIMPS ne sont pour l’instant que des particules hypothétiques. On les imagine pour résoudre le problème. Mais cette approche n’est pas ridicule, elle a déjà été utilisée avec succès : la découverte du neutrino a été bien précédée de sa description théorique. Elle a été imaginée pour résoudre un problème de masse manquante (tiens, justement !) dans une réaction nucléaire. De plus, les théories physiques évolués (entendez par là : celles qui n’ont pas encore été validées par l’expérience) en prévoient plusieurs : il y a le choix. Il est question de neutrinos, de neutralinos (théories supersymétriques) et autres axions. Aucune expérience ne les a encore mises en évidence, mais le LHC pourrait apporter sa pierre à cet édifice.
La présence de masses dans l’Univers, s’attirant mutuellement, est de nature à relentir cette expansion. Aussi, les cosmologistes ont toujours (depuis qu’on étudie la cosmologie) pensé que l’expansion ralentissait dans le temps, jusqu’à s’arrêter peut-être un jour, et même repartir en contraction (Big Crunch), mais cette vision a été contredite récemment.
Les super-novæ sont des étoiles massives qui explosent en fin de vie, en produisant pendant un temps bref autant d’énergie qu’une galaxie entière ! Aussi sont-elles visibles de très loin, plusieurs milliards d’années-lumière. Or on peut observer deux paramètres des super-novæ lointaines : le décalage spectral z, et la magnitude apparente m.
Lorsqu’une étoile émet de la lumière, celle-ci se répand dans tout l’espace autour d’elle. Il s’ensuit que son rayonnement se dilue, et que l’intensité baisse en fonction de la distance. La relation entre magnitude absolue, magnitude apparente et distance nous l’indique :
m - M = 5 log d - 5
Or l’étude des super-novæ de type SN Ia proches a montré qu’elles présentent toutes la même magnitude absolue, de l’ordre de -19,3, c’est-à-dire qu’elles produisent toutes la même quantité d’énergie. Ces explosions sont produites par l’accrétion de matière à une naine blanche, qui lui font atteindre la masse limite de Chandrasekhar. La matière provient d’un compagnon. Ainsi, toutes les SN Ia explosent avec exactement la même masse, ce qui explique l’identité des énergies, et en fait des chandelles standards.
Si on remplace M par -19,3 dans l’équation ci-dessus, on obtient une relation entre la magnitude apparente et la distance. Puisque la magnitude apparente est observable, on en déduit la distance que nous appellerons astrophysqiue (puisque définie à l’aide des propriétés astrophysiques des étoiles) dA = exp((m - M + 5) / 5), pour les SN Ia dA = exp((m + 24,3) / 5).
D’autre part, on peut mesurer le décalage spectral z (soit en prenant directement un spectre, soit en photographiant derrière trois filtres de couleurs différentes, et en comparant les résultats avec un spectre de corps noir). La loi dite de Hubble donne alors :
H0 dC = c z
en nommant dC la distance cosmologique de la SN. H0 et c sont des constantes, z est mesuré. Donc dC est connue.
Le problème qui apparaît alors est que ces deux distances ne sont pas compatibles ! Mesurées sur de nombreuses SN, les résultats sont têtus : ils diffèrent.
Pour expliquer cela, deux solutions sont envisageables. La relation entre magnitude apparente et magnitude absolue ne peut être mise en cause, c’est de la physique fondamentale. Alors, soit la magnitude absolue des SN Ia varie avec la distance (pour faire correspondre avec la distance cosmologique), soit c’est la distance cosmologique qui est en défaut, et la vitesse d’un objet ne serait pas une relation linéaire de sa distance.
On ne voit aucune raison pour admettre la première hypothèse. En effet, toute l’étude de l’Univers et toute la physique, sont basées sur le principe selon lequel les lois de la Nature sont les mêmes partout et en tout temps. Ce postulat est d’ailleurs bien vérifié par toutes les observations astrophysiques faites par ailleurs.
On est alors conduit à admettre que la relation n’est plus linéaire et qu’à grande distance, c’est-à-dire il y a longtemps, la valeur de H était plus petite. Donc, l’expansion s’accélère.
Cette conclusion est en contradiction avec tout ce qu’on pensait il y a quelques années. Elle met un terme à l’interrogation sur le devenir de l’Univers : il n’y aura pas de relentissement de l’expansion, qui se continuera éternellement, et de plus en plus rapide. L’Univers est destiné à se dissoudre dans l’espace, sa densité tendant vers 0. Mais ceci en moyenne seulement, car les condensations locales (galaxies, amas de galaxies), fortement liées par la gravité, sont destinées au contraire à se condenser de plus en plus. Lorsqu’il n’y aura plus de gaz libre, la formation de nouvelles étoiles s’arrêtera, et petit à petit l’univers deviendra froid et obscur… Mais nous avons encore quelques milliards d’années devant nous !!
Le décor est maintenant planté. Dans ses grandes lignes, l’histoire de l’Univers est simple : après une phase extrêmement chaude et dense, il se refroidit et les phénomènes physiques qui se déroulent sont déterminés par la température et la densité toutes deux décroissantes. Cependant, le modèle simple que l’on envisage ainsi pose quelques problèmes, que nous allons voir maintenant.
Problème de la platitude
L’Univers aujourd’hui nous apparaît pratiquement plat, c’est-à-dire que Ωtot = 1, aux erreurs de mesure près. Or cette valeur est instable ! En effet, si Ωtot est légèrement supérieur à 1, la densité de matière, donc la gravité, est trop forte, et l’Univers entre en contraction. Plus il se contracte, plus sa densité et sa gravité augmentent. Donc, la contraction s’accélère. De manière symétrique, si Ωtot est légèrement inférieur à 1, la gravité est trop faible, et l’Univers entre en expansion. Plus il se dilue, plus la gravité baisse, et donc l’expansion s’accélère. Comment comprendre alors que notre Univers soit actuellement si proche de la densité critique ? Depuis le Big Bang, il a eu le temps de mettre en œuvre cette instabilité, et de quitter définitivement cette valeur particulière. Pour que la valeur actuelle soit atteinte, il faudrait que Ωtot ait été égal à 1, à 10-5 près, 300.000 ans après le Big Bang, à 10-18 près une seconde après le Big Bang… et bien mieux encore plus avant.
Ceci nous rappelle que le destin de l’Univers est extrêmement sensible à sa densité initiale. Une variation de 10-24, vraiment infinitésimale, suffit à passer d’une expansion éternelle à une recontraction (Big Crunch). Comment se fait-il que l’Univers soit si vieux, puisque un infime excès par rapport à cette valeur aurait entraîné il y a longtemps la contraction ? C’est un premier problème des modèles de Big Bang. Il se traduit aussi en terme de courbure : un univers de densité critique est plat. C’est pourquoi on le nomme problème de la platitude(ou de la courbure nulle).
Problème de l’horizon
Il y a un autre problème. Très chaud au début, l’Univers était totalement ionisé lorsque les noyaux atomiques ont pu se former. Ils ont fini par capturer les électrons pour devenir neutres. C’est ce moment qui est visible dans le rayonnement de fond cosmologique.
En regardant à quelle époque la recombinaison a eu lieu, on trouve quelques 380.000 ans après le Big Bang, à une température de l’ordre de 3.000 K. Ceci correspond à un décalage spectral z = 1.100. Or les longueurs d’onde s’allongent proportionnellement au facteur d’échelle. Donc, celui-ci devait être 1.100 fois plus petit qu’aujoud’hui. Il est actuellement de 1 (par choix). Donc il était alors de a(t) = 1 / 1.100 = 0,0009.
L’Univers observable aujourd’hui a une taille de quelques 14 109 AL. Puisqu’au moment de la recombinaison, il était 0,0009 fois plus petit, cette portion d’Univers faisait à l’époque 14 109 AL × 0,0009 = 12,6 106 AL. Or l’Univers avait 380.000 ans. En 380.000 ans depuis le Big Bang, la lumière n’avait pu parcourir que 380.000 AL. Donc, la portion d’Univers qui a donné notre Univers observable aujourd’hui était considérablement plus grande (33 fois) que l’Univers observable de l’époque.
Au moment de la recombinaison, l’Univers observable était donc bien plus petit qu’aujourd’hui. Si petit en fait, que la lumière n’a pas pu aller très loin depuis le Big Bang. Alors, puisqu’aucune information n’a pu traverser tout l’Univers (observable aujourd’hui), comment se fait-il qu’à cette époque la température soit la même partout à 10-6 près ? Ce problème n’a pas de solution dans le modèle de Big Bang standard. C’est le problème de l’horizon.
Si on veut rendre compatibles ces deux caractéristiques, il faut admettre qu’avant l’époque du CMB, toutes les parties de l’Univers observable avaient été bien plus proches que ce qu’elle apparaissent alors. Donc, il faut admettre que l’expansion ait été bien plus rapide dans les premiers instants de l’univers. Voilà l’idée de base.
L’inflation doit s’être produite après la brisure de symétrie de Grande Unification, c’est-à-dire lorsque l’énergie était de l’ordre de 1015 GeV. En effet, avant cette brisure, l’énergie ambiante était suffisante pour créer de nombreuses paires particules-antiparticules, incluant des particules lourdes nommées monopôles magnétiques. Ces particules n’ont jamais été observées (le magnétisme se manifeste toujours par des dipôles, ayant un pôle nord et un pôle sud). Les théories indiquent que beaucoup de monopôles très massifs ont dû être créés, et il devrait en rester aujourd’hui. Le fait qu’on n’en détecte pas entre en contradiction avec ces théories. Sauf, si on suppose que l’inflation s’est produite après la brisure de symétrie qui a interdit la création des monopôles, et donc que presque tous les monopôles se sont anihilés avec leurs antiparticules. Alors, l’inflation a dilué l’espace très rapidement, faisant ainsi chuter la densité de monopôles à une valeur si faible que la probabilité d’en observer un aujourd’hui est suffisamment basse pour être compatible avec les observations.
L’un des problèmes, et non des moindres, consiste à trouver un moteur à cette inflation. Produite mathématiquement par la constante cosmologique, comment peut-on intrepréter cette dernière ?
Les idées actuelles consistent à imaginer un champ nouveau, dont le potentiel varierait. Ses variations expliqueraient le départ et l’arrêt de l’inflation. Mais il reste du travail avant d’avoir une idée claire de tout cela.

source du schéma : ipnweb.in2p3.fr
Quelle est la taille de l’Univers observable aujourd’hui ? Autrement dit, à quelle distance se trouvent aujourd’hui les objets les plus lointains que nous voyons ?
Une réponse naturelle serait de dire que, puisque l’Univers a 13 milliards d’années, son rayon est de 13 milliards d’années-lumière. Mais cette valeur ne tient pas compte de l’expansion, et se trouve bien fausse. En effet, pendant les 13 milliards d’années qui se sont écoulés depuis l’émission du signal, les distances se sont allongées. Et par conséquent, la distance entre le point d’émission et le point de réception (nous) aujourd’hui, est plus grande. Il suffit de comprendre que ce que nous voyons maintenant, c’est l’emplacement où était la galaxie lorsqu’elle a émis la lumière qui nous arrive enfin. Depuis, elle s’en est éloignée, ce qui fait qu’elle est plus loin que ce que le trajet de la lumière laisse penser.
Pour déterminer dans quelles proportions, utilisons la métrique de Robertson-Walker, qui est adaptée au problème, dans le cas particulier de la lumière, donc avec ds = 0 :
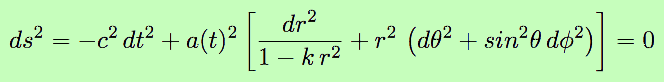
Considérons le cas d’un univers de courbure nulle (k = 0), ce qui ne saurait être très loin de la réalité. Puisque l’Univers est isotrope, on peut faire le calcul dans une direction particulière, le résultat sera le même dans toutes les autres. Choisissons donc dθ = 0 et dφ = 0. Il vient :
c2 dt2 = a(t)2 dr2
ou bien : c dt / a(t) = dr
Cette égalité s’intègre, entre 0 et t0 pour le terme de gauche, ce qui correspond à 0 et r0 pour celui de droite :
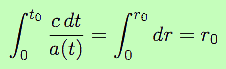
La seconde intégrale est évidente, elle donne r0. Pour la première intégrale, considérons que l’Univers est dominé par la matière. Alors, comme nous l’avons vu plus haut : a(t) = (t / t0) 2/3. Reportant cette valeur dans l’intégrale, celle-ci devient facilement calculable :
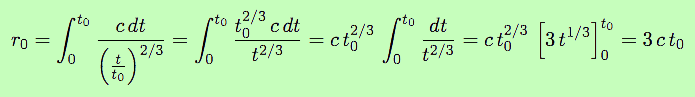
Donc, le point d’émission se trouve aujourd’hui à une distance trois fois supérieure à ce que l’on pourrait croire sans calcul. Quand on calcule une distance en multipliant le temps de parcours de la lumière par sa vitesse, on met en relation la galaxie observée, à l’époque où sa lumière l’a quittée, avec la nôtre, aujourd’hui. C’est donc ignorer l’éloignement de cette galaxie, par l’expansion de l’univers, depuis le départ de la lumière observée aujourd’hui...
La taille de l’Univers aujourd’hui est donc de l’ordre de 13 × 3 ≈ 40 milliards d’années-lumière, ou à peu près 13 Gpc.
La matière noire existe-t-elle ? C'est bien la question essentielle, car dans l'affirmative, elle domine très largement la matière ordinaire. Elle est considérée par deux communautés : les physiciens et les astrophysiciens.
Les physiciens font avancer la théorie des particules élémentaires et des interactions. Ils ont élaboré des théories un peu exotiques (supersymétrie entre autres, non validées par l’expérience), puis les ont testées dans les grands accélérateurs. À ce jour (c'est-à-dire à 14 TeV d'énergie), ils n'ont rien trouvé qui confirme ces théories. Aussi, la crédibilité de la matière noire est-elle bien ébranlée pour eux. Il reste la possibilité que ces particules aient une masse innaccessible pour les accélérateurs actuels.
Les astrophysiciens au contraire, observent l'univers et y voient des problèmes concernant sa dynamique. Les galaxies tournent trop vite pour leur masse, les amas de galaxies devraient se disloquer. Pour résoudre ces problèmes, le plus naturel est d'imaginer qu'il y a plus de matière que ce que l'on voit, c'est-à-dire qu'il existe une matière noire, invisible mais attractive, avec les propriétés adhoc. Ils ne voient guère comment résoudre ces problèmes par un autre paradigme. Pourtant, on peut imaginer que la gravitation soit en cause, mais la relativité générale est très solide.
Nous n'avons pas d'arguments décisifs pour trancher entre les deux actuellement. Mais le consensus ne fait pas loi !
Ce n'est pas parce que de nombreux astrophysiciens travaillent sur cette hypotéthique matière noire qu'elle acquiers une réalité. Ce n'est pas non plus parce que les physiciens des particules ne l'ont pas encore trouvée qu'elle n'existe pas. Il faut rester prudent, continuer les recherches dans ces deux directions. L'avenir apportera certainement une observation décisive qui permettra enfin de trancher entre les deux et mettra tout le monde d'accord !
---=OO=---