Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Relativité Générale | |||||||
Le chemin le plus court d’un point à un autre est la ligne droite,
à condition que les deux points soient bien en face l’un de l’autre…
Pierre Dac
Table des matières
1.1 Accélération
1.2 Espace-temps
2 Comparaison
3 Principe d’équivalence d’Einstein
3.1 Décalage spectral gravitationnel
3.2 Courbure des rayons lumineux
3.3 Ralentissement des horloges
3.4 Forces de marée
4 Chronogéométrie
5 Géométries non euclidiennes
5.1 Coordonnées de Gauss
5.2 Mollusque de référence
5.3 Métrique de Minkowski
5.4 Métrique de Schwarzschild
5.5 Coordonnées comobiles
5.6 Métrique de Robertson-Walker
6 Formalisme tensoriel
6.1 Tenseur métrique
6.2 Tenseur de Ricci
6.3 Tenseur impulsion-énergie
6.4 Equation d’Einstein
6.5 Trou noir
7 Vérifications de la théorie
7.1 Décalage gravitationnel
7.2 Eclipse totale de Soleil
7.3 Lentilles gravitationnelles
7.4 Ondes gravitationnelles
7.5 Frame dragging, ou effet Lense-Thirring
8 Résumé
Ce texte est une présentation informelle de la Relativité Générale. Il peut constituer une aide pour comprendre ses fondements, et ses relations avec les autres théories de gravitation.
La lecture de ce chapitre est facilitée par la connaissance des notions définies dans la Relativité Restreinte.
��La Relativité Générale a été publiée par Albert Einstein en 1915, dix ans après la Relativité Restreinte. Elle vient pour supprimer la limitation conservée par cette dernière, depuis la Relativité Galiléenne, de ne considérer que les observateurs galiléens. La Relativité Générale prend en compte tous les observateurs, même s’ils sont accélérés. En ce sens, la Relativité Générale est une écriture universelle des lois de la physique.
Elle abandonne la structure sous-jacente, fixe, de l’espace-temps, pour l’amalgamer à son contenu matériel. L’équation d’Einstein dit simplement que la géométrie de l’espace-temps est égale à son contenu matériel. Ainsi, la géométrie est déformée pas les masses, et les mobiles suivent des géodésiques de cet espace courbe.
Le formalisme mathématique utilisé pour décrire cette géométrie est l’algèbre tensorielle.
On appelle accélération toute opération qui modifie l’état de mouvement d’un objet, c’est-à-dire tout ce qui change sa vitesse. N’oubliez pas que la vitesse a une direction et un sens : il n’est pas équivalent d’aller vers l’est ou d’aller vers l’ouest, même si on y va dans les deux cas à 50 km h-1 (50 km / h) ! Alors, lorsqu’on change de direction, même en conservant la même valeur de la vitesse (en km h-1), on subit une accélération, et le référentiel qui la subit n’est plus galiléen.
La Relativité Restreinte a apporté la définition de l’espace-temps comme théatre des phénomènes. Bien que le temps se soit trouvé mélangé à l’espace dans ce nouveau concept, l’espace-temps existe en dehors de son contenu. La Relativité Générale est à ce point de vue une rupture essentielle : nous verrons qu’à propos de la gravité (Relativité Générale), il ne s’agira plus d’un espace-temps externe, théatre des phénomènes, mais d’un espace-temps acteur lui-même, qui participe au phénomène en se déformant sous l’effet des masses et de l’énergie. Ce sont ces déformations qui guident les mobiles.
La Relativité Restreinte décrit la physique de manière à respecter le principe de Relativité. Ceci signifie que les lois de la physique doivent être invariantes dans un changement de référentiel galiléen, c’est-à-dire sous la transformation de Galilée. Les référentiels galiléens ne tiennent, par nature, pas compte des accélérations, puisqu’ils sont en translation uniforme. La Relativité Générale est donc venu pour combler cette lacune, et donc décrire les lois de la physique de telle façon qu’elles soient invariantes dans un changement de référentiel quelconque, accéléré ou non.
Ceci pour dire que pendant le vol de croisière d’un avion, en négligeant les turbulences, on est emporté dans un mouvement de translation uniforme. L’avion constitue donc un référentiel galiléen, et on peut y appliquer la Relativité Restreinte. Par contre, pendant les phases de décollage et d’atterrissage, le mouvement est accéléré, et la Relativité Générale peut seule déterminer précisément le mouvement.
Dans l’étude des mouvements accélérés, on distingue deux situations : celle dans laquelle on communique un mouvement en appliquant une force, et celle dans laquelle le corps tombe dans un champ de gravitation. Elles sont fondamentalement différentes, mais partagent une même forme de proportionnalité.
Ce sont a priori deux notions très différentes. Cette distinction est très importante, et elle se manifeste dans la vie courante (bien qu’on n’en ait pas conscience) : soulever un objet, et le lancer, sont deux choses bien différentes. Pour le soulever, on lutte contre la pesanteur, produite par la Terre et dirigée vers elle (verticalement), alors que pour le lancer (horizontalement), on le propulse perpendiculairement à la direction du poids. Donc, dans ce cas, le poids ne change pas. On ne devrait pas ressentir d’effort pour cela. Pourtant, on sent bien la force nécessaire pour animer l’objet. Poids, et résistance à la mise en mouvement, sont donc deux notions différentes, mais que nous mélangeons dans notre expérience. Physiquement, on doit les séparer, et Einstein a bien insisté la-dessus.
Si nous ne faisons pas la différence entre ces deux phénomènes, c’est certainement parce que dans notre environnement terrestre, elle ne se manifeste pas de manière sensible. Il faut un raisonnement pour la mettre en lumière. Et la cause de cela est que les deux masses ont la même valeur !!! Les physiciens en ont fait un principe :
Il est utilisé en physique depuis très longtemps.
Remarquez de plus que parmi toutes les forces qui s’appliquent à un corps, seules les forces d’inertie et gravitationnelle dépendent de la masse. Les autres dépendent de charges spécifiques, charge électrique, charge de couleur.
Einstein est allé un peu plus loin dans cette équivalence. Si on réalise des expériences locales (à courte distance, disons dans la cabine d’un ascenseur��), on peut considérer que le champ gravitationnel est homogène, car :
Il n’y a alors aucune différence entre une chute libre dans ce champ homogène, et une absence totale de champ. Einstein en déduit le principe d’équivalence fort :
Ce principe pose donc qu’une accélération -une augmentation ou diminution de vitesse- produit des effets identiques à un champ de gravitation. Se laisser tomber en chute libre, c’est accélérer son mouvement exactement comme la pesanteur le demande. C’est donc en annuler les effets, et c’est pourquoi un astronaute dans sa cabine flotte librement : il tombe exactement comme la cabine. Dans le référentiel de la cabine en chute libre, la gravité est donc nulle.
Note : on appelle impesanteur la situation dans laquelle on ne ressent pas de pesanteur. Ce terme remplace celui d’apesanteur, pour éviter toute confusion entre "la pesanteur" et "l’apesanteur", deux choses contraires, mais phonétiquement identiques.��
Réciproquement, une accélération peut avoir les mêmes conséquences qu’un champ de pesanteur :
Dans la cabine en chute libre, si on lance une boule avec une vitesse v, celle-ci continuera le mouvement imprimé en ligne droite, à vitesse constante (par rapport à la cabine). On a pu le vérifier souvent avec des images de cosmonautes qui jouent avec un stylo ou autre petit objet. Ceci montre que le référentiel propre de la cabine, accéléré par le champ de pesanteur, est un référentiel inertiel (dans lequel le mouvement inertiel se réalise). Un référentiel inertiel est donc un référentiel auquel la somme des forces appliquées est nulle.
Ce principe a des conséquences totalement insensibles dans la vie courante : le décalage spectral gravitationnel, la courbure des rayons lumineux et le ralentissement des horloges, le tout dans un champ de gravitation.
Rayon lumineux longitudinal Considérons une fusée qui accélère avec l’accélération g. Au plancher de la cabine se trouve un émetteur de lumière. Il émet un rayon qui sera capté par un détecteur situé au plafond. Le rayon part à l’instant t0, alors que la fusée se déplace à la vitesse v0. La distance entre l’émetteur et le récepteur est h. Le rayon mettra donc le temps t = h / c pour atteindre le récepteur. Mais la fusée accélère. Pendant le temps T, sa vitesse augmente de Δv = g t = g h / c. Donc, lorsque le rayon arrive sur le récepteur, la vitesse de celui-ci a augmenté de Δv. Le récepteur s’éloigne du rayon, et la longueur d’onde de celui-ci apparaît donc décalée vers le rouge par effet Doppler-Fizeau. Si la fusée accélérait vers le bas, le décalage serait vers le bleu.
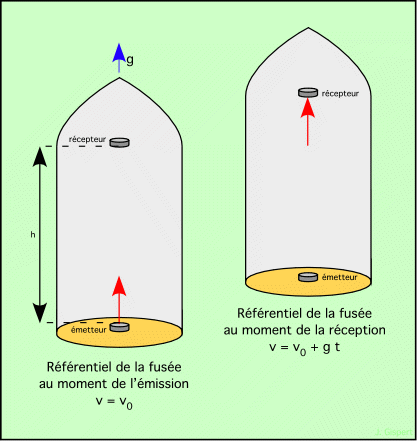
Figure 1.1 : Fusée en accélération
En vertu du principe d’équivalence des référentiels, même accélérés, on doit observer le même phénomène dans un référentiel (cabine) fixe placé dans un champ gravitationnel d’accélération égale. Or cette observation a été faite avec un résultat en parfait accord avec la théorie. Ceci renforce donc la confiance dans le principe d’équivalence entre accélération et champ gravitationnel.
On admet ce phénomène en vertu du principe d’équivalence, et on le valide par l’expérience. Mais pour le comprendre, on peut penser que le photon émis en bas d’un champ de gravitation possède une énergie E = h ν, fonction de sa couleur. Pour monter verticalement, il doit perdre un peu d’énergie. Ce faisant, sa vitesse ne change évidemment pas, mais sa fréquence baisse. Et donc, en atteignant le récepteur, sa fréquence est ν′ < ν, avec l’énergie correspondante E′ = h ν′ < h ν.
Rayon lumineux transversal Considérons notre fusée, avec la source lumineuse maintenant à gauche, et le récepteur à droite. Dans le référentiel de la fusée, le rayon se propage en ligne droite. Mais vu de la Terre, lorsqu’il touche le récepteur, la fusée est plus loin. Son mouvement étant accéléré, la vitesse a varié pendant ce laps de temps, et donc la trajectoire observée du rayon lumineux est un arc de courbe.
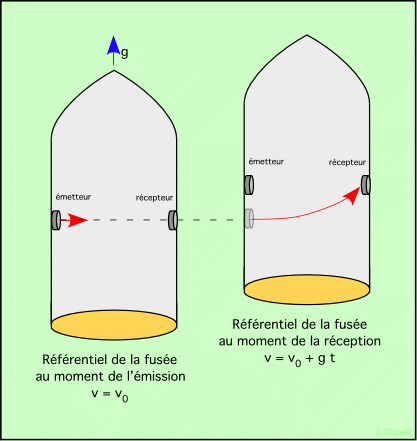
Fig. 1.2 : courbure des rayons produite par une accélération
On remarque que la courbure (flèche rouge) se fait dans le sens de l’accélération (flèche bleue).
Encore une fois, en vertu du principe d’équivalence, ce mouvement accéléré est équivalent à un champ de gravitation. Donc, dans un champ de gravitation, le rayon lumineux doit également suivre une trajectoire courbe, et la courbure se fait dans le sens de l’accélération. L’effet est très faible, ce qui explique qu’il n’ait jamais été mis en évidence expérimentalement avant sa prédiction théorique.
Nous verrons plus loin demultiples confirmations de cette théorie.
Nous allons utiliser le principe d’équivalence entre les référentiels accélérés et les référentiels placés dans un champ de gravitation pour déterminer le ralentissement des horloges.
Considérons un disque en rotation, avec une horloge placée au centre (donc sans vitesse), et une autre identique à la périphérie. Cette dernière se déplace en tournant à une vitesse v = ω r (ω est la vitesse angulaire de rotation). La Relativité Restreinte est applicable à ces deux horloges, et en fonction de leur vitesse relative, prédit un ralentissement de l’horloge extérieure par rapport à l’horloge centrale. Donc, une accélération produit un ralentissement des horloges, et puisque cette accélération est équivalente à un champ de gravitation, il en est de même pour celui-ci.
La vérification de ce phénomène est difficile, car il est très faible. Mais elle a cependant été réussie dans le faible champ gravitationnel de la Terre, et constitue une éclatante vérification de la Relativité Générale.
La figure 1.2 montre un objet massif sphérique (planète, étoile à neutrons par exemple). Y figurent deux trajectoires de chute libre, qui convergent vers le centre du corps attracteur. Une particule placée en A1 est soumise à la gravité. Un peu plus tard, elle est en A2 étant tombé vers le corps central.
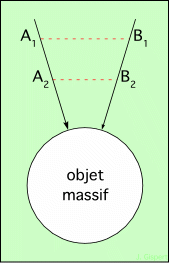
Fig. 1.2 : Champ gravitationnel
Première constatation : le champ gravitationnel de l’objet diminue lorsqu’on s’éloigne : il varie en 1 / r2, où r est la distance au centre. Plaçons deux particules en A1 et A2. La plus proche du corps central, en A2, ressent une gravité plus importante, et donc accélère plus fortement que l’autre. Donc elle s’en éloigne, puisque l’autre tombe moins vite. Lorsque la seconde sera arrivée en A2, elle ressentira une gravité plus forte également, mais la première sera encore plus proche du centre, et son accélération sera toujours supérieure. Par conséquent, cette différence de gravité en fonction de l’éloignement produit une séparation des deux particules, qu’on peut interpréter comme une force tendant à les éloigner l’une de l’autre. C’est une force fictive en ce sens qu’elle n’est due qu’à la différence entre deux forces réelles, mais ses effets sont bien réels. Dans le référentiel lié à A1 (resp. A2), on voit A2 (resp. A1) s’éloigner.
Si ces deux particules appartiennent à un objet solide, cette force de marée s’oppose à la force de liaison entre elles (qui les maintient ensemble). Si la force de marée est plus forte que les forces de cohésion, l’objet se cassera (l’endroit le plus lointain du centre attractif où ceci se produit est la limite de Roche).
Seconde constatation : vous remarquerez par ailleurs que chaque particule tombe vers le centre de l’objet massif, donc leurs trajectoires se coupent au centre du corps attracteur. Par conséquent, dans leur mouvement, elles se rapprochent l’une de l’autre : la distance A2B2 est plus petite que la distance A1B1. Tout se passe donc comme s’il y avait une force qui pousse les deux objets qui tombent à se rapprocher l’un de l’autre, perpendiculairement à leur direction de chute. Cette force est une force de marée. Elle est aussi fictive que la précédente, étant comme elle due à la différence entre les forces appliquées aux deux particules.
Si on laisse tomber un objet étendu, un rectangle A1 B1 B2 A2, il subit cette force, étant comprimé dans sa largeur et étiré dans sa longueur.
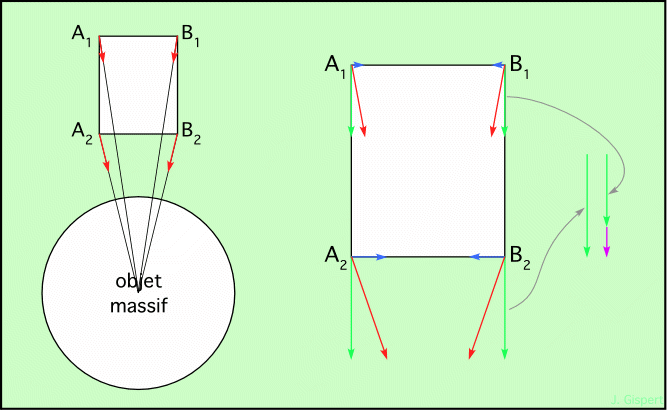
Fig. 1.3 : Détail du champ gravitationnel
Sur la partie gauche, les flèches rouges indiquent la direction et l’intensité de la force d’attraction ressentie par chaque point (l’intensité est donnée par la longueur des flèches). La partie droite du schéma montre le détail de la force appliquée aux 4 points considérés. La décomposition de ces forces selon deux axes perpendiculaires met en évidence les forces de marée (flèches bleues) qui compriment l’objet. Dans l’autre direction, les flèches vertes représentent la composante verticale de l’attraction ; elles sont reportées tout à droite du schéma, et leur différence est représentée par la flèche violette. Cette dernière représente donc la force d’étirement produite par la différence de gravité entre deux points de distance au centre différente. Vu du point B1 par exemple, la flèche violette représente la force qui éloigne B2.
Les explications qui précèdent sont donnnées dans un langage newtonnien. Mais on peut interpréter le rapprochement des trajectoires au voisinage de l’objet massif de deux façons différentes :
Dans la première de ces interprétations, les forces de marées apparaissent comme des forces fictives, n’ayant pas de source précise. De plus, leur action instantanée est en contradiction avec la Relativité Restreinte.
Dans la seconde interprétation, les particules en chute suivent tout simplement des trajectoires naturelles, dans un espace courbe. Expliquons cela par analogie : la surface de la Terre nous semble grossièrement plate, mais elle ne l’est pas, même localement. Elle est parsemée de bosses et de creux, que sont les montagnes et les vallées. Où coule la rivière ? dans le fond de la vallée, car c’est l’endroit où son énergie potentielle est minimale (attirée par la Terre, l’eau tombe tant qu’elle le peut). Dans l’espace courbe qu’est la surface du sol montagnard, le torrent suit une géodésique : c’est une courbe de moindre énergie.
Par analogie, on peut considérer que les deux particules A1 et B1 précédentes tombent simplement selon une trajectoire naturelle dans un espace courbe. Si l’espace était plat, leurs trajectoires seraient parallèles et parcourues à vitesse constante, mais puisque l’espace est courbé, elles se coupent au centre de l’objet attracteur et la vitesse augmente au cours de la chute. La courbure de l’espace est produite par l’objet attracteur.
La Relativité Générale se fonde sur la géométrie de l’espace-temps, déterminée par le contenu en matière-énergie de l’Univers. C’est là l’idée originale d’Einstein. Généralisant le principe d’inertie, il a imaginé que les corps se déplacent toujours selon ce principe, mais dans un espace-temps déformé par la matière. Le principe d’inertie galiléen indique qu’une particule se déplace, tant qu’elle n’est pas soumise à des forces, en ligne droite. Mais qu’est-ce qu’une ligne droite ? C’est le chemin le plus court pour relier deux points. Or à la surface d’une sphère par exemple, la ligne de plus court chemin n’est pas une droite, mais un arc de grand cercle : c’est la trajectoire suivie par les avions à la surface de la Terre. Si l’Univers était à deux dimensions, et de forme sphérique, les mobiles inertiels parcouraient donc des arcs de grand cercle. Ils seraient tout naturellement contraints de rester dans leur espace ! L’arc de grand cercle y est la ligne la plus rapide pour aller d’un point à un autre.
Partant de cette idée, Einstein a envisagé que notre espace-temps ne soit pas plat, comme l’intuition courante nous le fait croire, mais parfois courbé. Alors, un mobile inertiel, comme par exemple une planète autour du Soleil, suivrait une trajectoire qui épouse la forme de l’espace-temps. Au voisinage du Soleil, il est évident que la déformation doit avoir la symétrie sphérique. Et donc que la trajectoire inertielle de la planète doit tourner autour…
La déformation de l’espace-temps produite par une masse est d’autant plus forte que l’on est plus près. La courbure de l’espace est donc plus importante qu’à grande distance, c’est pourquoi les planètes proches vont plus vite. Dans l’autre direction, un objet qui tombe en chute libre rencontre, en avançant, un espace-temps de plus en plus courbé, et c’est pourquoi sa vitesse augmente.
Il faut donc voir la modélisation de la gravité par la géométrie comme faisant intervenir également le temps. D’où le nom de chronogéométrie qu’on peut attacher à cette description de l’espace-temps.
Pour faire intervenir le temps, il suffit de l’incorporer à la description de la même manière que l’espace, donc de l’introduire comme quatrième variable après les trois variables d’espace. Mais la géométrie sera semblable, avec cette dimension de plus. Il faut donc d’abord étudier la géométrie elle-même.
Géométrie euclidienne C’est la géométrie de l’école, qui nous semble si naturelle qu’on ne saurait la remettre en question. Sur quoi est-elle basée ? Sur des observations, et c’est ce qui fait sa force.
Malgré cette base expérimentale, la Géométrie euclidienne est une abstraction pure. Accrochons deux pendules (ficelle soutenant une petite masse), au plafond. Ils se positionnent verticalement sous l’effet de la pesanteur. Visuellement, les ficelles sont parallèles. Plus précisément, si on mesure leur distance aux deux extrémités, on trouve bien sûr la même valeur. Si on prolonge par la pensée ces deux ficelles, on obtient la notion euclidienne de parallèles : ce sont deux droites qui ne se rencontrent jamais (elles gardent constante leur distance). A partir de là, Euclide a bâti toute sa Géométrie, celle qui est toujours enseignée au niveau élémentaire. Le nom même Géométrie signifie en grec : mesure de la Terre. Il montre bien que cette théorie est basée sur des observations pratiques.
L’abstraction vient de l’erreur commise en mesurant les distances des deux ficelles en haut et en bas. Il est impossible de mettre en évidence une différence, pourtant cette différence existe. Et le vrai prolongement des ficelles donne deux droites qui se coupent au centre de la Terre. La Géométrie euclidienne est donc basée sur une erreur de mesure. Remarquez de plus que la géométrie d’Euclide serait la bonne, s’il n’y avait pas la Terre… C’est bien la preuve que la présence de la Terre a une influence sur la géométrie (au-delà du nom…). Et ce qui fait que la Relativité Restreinte ne s’adresse, strictement, qu’à un Univers vide.
Euclide a eu du génie, car il a résumé sa Géométrie en cinq postulats, dont le dernier a donné des sueurs aux mathématiciens pendant des siècles. Ce dernier postulat dit que "dans un plan, par un point extérieur à une droite on peut faire passer une parallèle à cette droite, et une seule". Ce postulat avait, pour les mathématiciens, des allures de théorème : ils en ont cherché vainement une démonstration à partir des quatre premiers. L’échec de ces recherches ne prouve pas l’impossibilité de démontrer. La démonstration pourrait être trop difficile pour avoir été trouvée. Mais Gauss, dès 1817, a soupçonné que ce postulat ne pouvait pas être démontré ; on dit dans ce cas qu’il est indépendant des autres.
C’est Gauss qui est à l’origine de ces géométries. Il a créé une géométrie sur la surface d’une sphère, la géométrie elliptique, dans laquelle les géodésiques sont les intersections avec la surface, des plans passant par le centre. Ce sont donc les grands cercles de la surface. Par deux points distincts passe une droite et une seule. Mais étant donnés une ligne et un point extérieur à cette ligne, il n’existe pas de ligne passant par ce point et ne la coupant pas. Donc, il n’existe pas de parallèle à la ligne donnée passant par le point. Cette géométrie satisfait à tous les autres axiomes d’Euclide. C’est donc la première géométrie non euclidienne.
L’existence de géométries qui satisfont les premiers postulats d’Euclide, mais pas le cinquième, prouve que ce dernier en est indépendant. Euclide a donc admis que par un point extérieur à une droite passe une parallèle et une seule. On peut postuler, à la place, que par ce point ne passe aucune doite parallèle à la droite donnée, on obtient la géométrie de Riemann, ou au contraire qu’il y en a une infinité, et on obtient les géométries hyperboliques de Lobatchevski et Boliyai.
Choix d’Einstein Sur la sphère, l’arc de grand cercle est parcouru à vitesse constante. On peut donc bien considérer que c’est un mouvement inertiel, le long d’une ligne qui est la plus droite possible. Définissons alors ces lignes naturelles, que nous appellerons géodésiques, comme étant les lignes parcourues par des mobiles inertiels. Précisons que inertiel signifie : sans subir de forces extérieures.
On peut encore généraliser cette idée, en considérant des mouvements accélérés (donc non inertiels au sens classique). Considérons un objet en chute libre (qui ne subit d’autre force que la gravité), vers un corps central. Il tombe en ligne droite, radiale, vers le centre de l’attracteur. Mais son mouvement est accéléré. Si on imagine que l’espace-temps est modifié par la masse centrale de telle manière que les intervalles d’univers soient modulés en fonction de la distance au centre, alors l’objet en chute libre suit une trajectoire inertielle dans cet espace-temps. Par conséquent, en modélisant la géométrie de l’espace-temps par les masses présentes, on peut ramener tout mouvement à un mouvement inertiel.
Cette idée étant posée, il reste à la formaliser. Pour cela, il faut décrire la géométrie de l’espace-temps, et dire qu’elle est équivalente à son contenu matériel… La description de l’espace-temps se fait par l’intermédiaire de la métrique.
Les coordonnées de Gauss sont des coordonnées curvilignes. On a l’habitude de mesurer les longueurs sur des règles droites. Pourtant, losqu’un tailleur prend vos mesurations, il utilise un mètre de couturière, ruban souple gradué qui s’adapte à la forme du corps pour en obtenir les mesures. Les coordonnées de Gauss sont basées sur ce principe : elles sont mesurées le long de lignes pouvant être courbes.
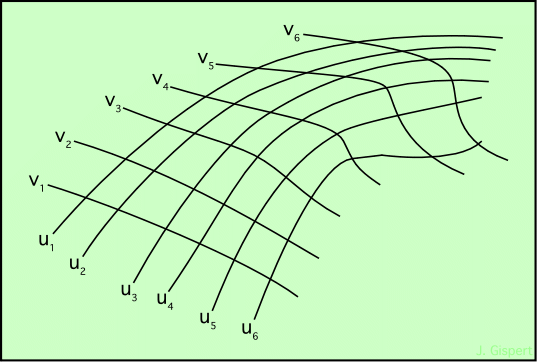
Pour mesurer un plan, il faut habituellement deux droites perpendiculaires graduées (coordonnées cartésiennes). On détermine la position d’un point en y faisant passer deux parallèles aux axes de coordonnées. Par définition, les parallèles issues de deux points différents ne se coupent pas. Pour les coordonnées de Gauss, c’est la propriété qui est retenue : les courbes le long desquelles on mesure les longueurs ne doivent pas se couper. Et naturellement, entre deux courbes quelconques, il doit en exister une qui vérifie aussi la propriété.
L’étude de la gravitation faite par Einstein lui a montré qu’il n’est pas possible de trouver un corps rigide qui serve de point de repère. Dans un champ gravitationnel, ce corps doit se déformer, pour s’adapter. On peut toujours imaginer et trouver un champ assez intense pour cela, : c’est le cas des marées, qui déforment le géoïde, c’est aussi le cas d’un satellite qui tournerait autour de sa planète en deça de la limite de Roche. Puisqu’on ne peut pas trouver de corps rigide qui convienne pour matérialiser un référentiel, Einstein a imaginé un objet assez souple pour s’adapter aux différentes conditions qu’il rencontre.
C’est un tel objet qu’il nomme mollusque de référence.
Il a la propriété correcte de suivre les déformations de l’espace-temps. Mais il conserve la notion intuitive de séparation entre coordonnées d’espace et de temps, ce que la théorie ne justifie absolument pas.
Les référentiels étant maintenant donnés, il faut définir les relations entre points voisins, et ceci se fait par la définition d’une métrique. La métrique est la distance qui sépare deux poits voisins. Nous avons déjà vu, en Relativité Restreinte, la métrique de Minkowski qui lui est appropriée. Mais il faut définir d’autres métriques adaptées à diverses situations.
La métrique décrit les propriétés locales de l’espace-temps. Elle donne la distance infinitésimale entre deux points voisins. Les propriétés de l’Univers n’étant pas forcément identiques en tous points, la métrique ne doit pas être la même partout !
Considérons d’abord l’Univers à très grande échelle, où le Principe Cosmologique s’applique. Si la courbure est nulle, c’est-à-dire si l’Univers est euclidien, la métrique de Minkowski est pertinente :
![]()
Elle est définie en coordonnées cartésiennes (les coordonnées habituelles), et décrit un espace-temps localement plat. Nous l’avons déjà rencontrée en Relativité Restreinte, où la présence des masses n’est pas considérée. Pour la Cosmologie, ou l’étude des objets compacts, il faut définir une métrique différente, capable de représenter les déformations géométriques de l’espace-temps.
Au voisinage d’un corps massif (étoile normale, naine blanche, étoile à neutrons, trou noir), il est bien évident que la gravité est forte, et que le champ gravitationnel présente la symétrie sphérique. Dans ce cas, c’est la métrique de Schwarzschild qui s’applique :
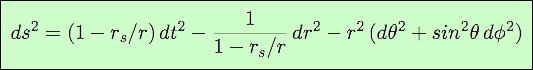
Elle est définie en coordonnées sphériques, qui représentent naturellement la symétrie de l’espace autour d’un objet compact.
La métrique montre un premier terme qui dépend du temps. Son coefficient dépend d’une constante rs. A l’extérieur de l’objet compact, r > rs. Donc le coefficient de dt2 est inférieur à 1. Tant qu’on reste loin de l’objet, le coefficient vaut pratiquement 1. Le second terme présente le même coefficient, mais au dénominateur. Il vaut 1 également à grande distance. La métrique se réduit alors à ds2 = dt2 - dr2 - r2 (dt2 + sin2 dφ2), qui est la métrique de Minkowski exprimée en coordonnées sphériques. Ceci signifie que, loin d’une masse, l’espace-temps reprend sa forme euclidienne. Par contre, à courte distance, il est réellement déformé.
rs = 2 G M / c2 (exprimé en unités usuelles) est le rayon de Schwarzschild. La complexité de cette métrique est justifiée par la déformation de l’espace-temps imposée par le corps massif. Au voisinage des corps massifs (étoiles à neutrons, trous noirs…), c’est elle qui doit être considérée.
Le sinus qui apparaît est dû à l’utilisation des coordonnées sphériques.
Avant de décrire la métrique FLRW, il faut définir un système de coordonnées adaptées à décrire un Univers non statique.
Les coordonnées comobiles sont indispensables en cosmologie, et plus généralement en Relativité. Considérons deux points dans l’espace-temps, dont la distance instantanée est d. Si l’espace est en expansion, la distance d croît avec le temps. Il faut donc remplacer la variable par une fonction du temps. Mais imagninez qu’on dessine dans l’espace-temps, une grille régulière qui représente les coordonnées. Si l’espace-temps est en expansion, la grille qui lui est attachée croît avec lui. Et donc la distance mesurée sur cette grille reste constante. Puisque l’accroissement de distance entre les galaxies n’est pas dû à un déplacement de ces galaxies, mais à une dilatation de l’Univers entre elles, il est logique de considérer que leur distance reste constante. C’est ce que permettent les coordonnées comobiles.
Soit r(t) la distance entre deux points A et B. Elle est variable, en fonction de l’évolution de l’espace-temps, c’est-à-dire en fonction du temps t. Mais cette évolution est la même en tous points, d’après le principe cosmologique. Donc, elle ne dépend pas des coordonnées d’espace. Soit d la distance comobile entre ces points. Elle est constante, mais bien sûr r(t) est fonction de d. On le traduit par l’écriture :
r(t) = a(t) d
La nouvelle fonction a(t) ainsi définie, représente la variation de la distance en fonction du temps, et se nomme facteur d’échelle. d représente la distance comobile, c’est-à-dire comme si l’expansion n’existait pas. Comme nous venons de le voir, le facteur d’échelle ne dépend que de t.
On peut illustrer les coordonnées comobiles par un schéma :
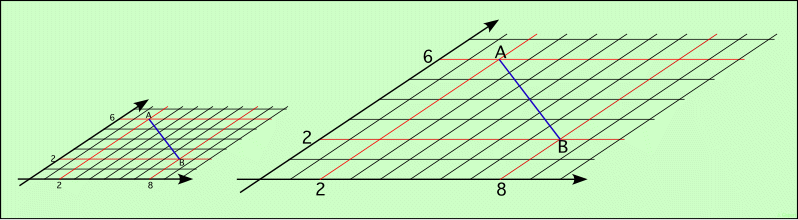
Supposons que l’espace entre les galaxies soit quadrillé, et que le quadrillage s’écarte avec l’expansion, comme s’il était peint dans l’espace-temps lui-même. Le schéma montre les coordonnées comobiles d’une partie de l’Univers à deux instants différents. A gauche, l’Univers est encore contracté ; les points A et B, qui représentent deux galaxies, ont les coordonnées (2, 6) et (8,2). La distance entre A et B est de 7,2 unités (théorème de Pythagore).
Plus tard, à droite, les distances dans l’Univers ont doublé. Mais la grille de coordonnées a aussi doublé, et les points A et B sont toujours en (2, 6) et (8,2). Le calcul de la distance entre A et B donne toujours 7,2 en unités comobiles. Ainsi, la distance comobile entre les deux galaxies, mesurée sur ce quadrillage, ne change pas ! Les deux galaxies sont au repos dans leur système de coordonnées, c’est l’espace-temps qui s’agrandit entre elles.
Mais en coordonnées réelles, r(t) = a(t) d. Puisque nous avons dit que les distances réelles avaient doublé, on peut écrire à l’instant t2 de la figure de droite :
r(t2) = 2 d
Où l’on voit que la distance comobile étant la même, la distance réelle est bien doublée !
Le quadrillage définit un système de coordonnées nommées coordonnées comobiles. Notons r la distance entre les deux galaxies, et x la distance comobile entre elles. L’une varie, l’autre non. Notons a(t) la proportion entre les deux :
r(t) = a(t) x
On appelle facteur d’échelle la fonction a(t). Elle décrit l’expansion de l’Univers en fonction du temps.
C’est la métrique générale adaptée à la description de l’Univers. Elle suppose l’espace-temps homogène.
Elle est parfois notée métrique FLRW, rappellant tout de même qu’elle a été définie d’abord par Friedmann et Lemaître ! Elle est définie par :
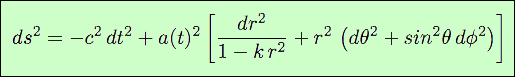
La métrique, adaptée à l’étude globale de l’Univers, utilise les coordonnées comobiles, compatibles avec le principe cosmologique.
Le principe de Relativité énonce que tous les référentiels sont équivalents. Or un référentiel est défini par un système de coordonnées. Donc, les lois de la physique doivent être réécrites dans un formalisme indépendant d’un système de coordonnées particulier. Et ceci est bien naturel, puisque les déformations sont locales, donc différentielles (la physique décrit les différences entre deux points voisins). C’est le calcul tensoriel qui permettra de représenter les lois dans ces conditions.
Pour écrire l’équation fondamentale d’Einstein, il faut donc représenter mathématiquement ces déformations géométriques. Ce problème est compliqué, mais il avait déjà été résolu par Riemann et Lobatchevski, qui avaient fondé les géométries non euclidiennes. Elle s’appuie sur un tenseur (tableau de nombres) de dimension 4 (4 × 4 nombres), qui comprend donc 16 valeurs :
| a11 | a12 | a13 | a14 |
| a21 | a22 | a23 | a24 |
| a31 | a32 | a33 | a34 |
| a41 | a42 | a43 | a44 |
Chaque ligne, et chaque colonne, correspond à l’une des 4 variables x, y, z, t (ou à d’autres coordonnées si l’espace-temps est décrit différemment).
Il est rare que toutes les valeurs soient indépendantes. Prenons par exemple le tenseur métrique gμν pour la métrique la plus simple, celle de Minkowski ds2 = c2 dt2 - dx2 - dy2 - dz2 :
| gμν = |
|
On voit, sur la diagonale, les coefficients du ds2 : c2 coefficient de dt2, et -1 pour les trois autres.
L’algèbre tensorielle est basée sur le calcul linéaire : en multipliant deux fois ce tenseur par le vecteur (dt, dx, dy, dz), on obtient le ds2 de la métrique de Minkowski. Il constitue donc une représentation de cette métrique. Mais sa présentation est bien plus riche, car les calculs effectués grâce à lui permettent de manipuler en bloc plusieurs équations différentes.
Le tenseur métrique ci-dessus ne comporte que 4 composantes non nulles. D’autres tenseurs en ont un peu plus. Par exemple, si le tenseur est antisymétrique, les valeurs opposées par rapport à la diagonale qui contient les 0, doivent être égales en valeur absolue, mais de signes opposés :
| gμν = |
|
Les cellules qui ont les valeurs opposées sont représentées de la même couleur. Sur la diagonale, la seule façon de satisfaire à aii = -aii est 2 × aii = 0, soit aii = 0. Il ne reste que 6 valeurs différentes (celles situées au-dessus de la diagonale par exemple, les autres s’en déduisant par changement de signe).
Le tenseur métrique le plus général possède effectivement 16 coefficients. Mathématiquement, le coefficient aij représente le produit scalaire du vecteur de base ei par le vecteur de base ej.
Le tenseur de Ricci (formulé par Gregorio Ricci-Curbastro) permet, par des valeurs appropriées, de représenter la géométrie locale de l’espace-temps. Il décrit comment varient les vecteurs de base (les axes de coordonnées et leurs unités). Il représente donc les déformations de l’espace entre deux points voisins. Dans la figure 1.3, les flèches rouges montrent l’attraction ressentie en chaque point du rectangle. Le tenseur de Ricci correspondant exhiberait les différences entre ces flèches, de façon à pouvoir calculer les différents points à partir de l’un d’eux. Si je connais le point A, et si je sais que autour de A la variation du coefficient de x est de dx, je peux calculer la valeur de x au point B. Idem pour les autres coordonnées.
Ainsi, de proche en proche, on pourra calculer une trajectoire complète par transformations successives.
Le tenseur impulsion-énergie décrit le contenu énergétique de l’espace-temps, en fonction de la matière et de l’énergie qui s’y trouvent (puisque la matière est équivalente à de l’énergie en vertu de E = mc2). Comme les tenseurs précédents, il décrit non pas le contenu absolu, mais son évolution d’un point à un point voisin. C’est lui qui décrit donc l’action des masses, et des énergies, qui agissent dans l’espace-temps.
Nous pouvons maintenant écrire l’équation d’Einstein. Nous avons dit que la Relativité Générale décrit la géométrie de l’espace-temps en fonction de son contenu matériel (et énergétique). Pour cela, l’équation d’Einstein égale simplement un tenseur représentant la géométrie de l’espace-temps (notons-le G pour l’instant), à un autre représentant son contenu matière-énergie (noté E). La géométrie est donc modelée par la matière et l’énergie présentes.
L’équation d’Einstein s’écrit :
G = E
Nous avons supposé que toute la description de la géométrie était comprise dans le tenseur G, et toute la description de la matière-énergie dans le tenseur E. La situation n’est évidemment pas aussi simpliste, mais la structure générale de l’équation est bien celle-là. De manière plus détaillée, l’équation s’écrit :
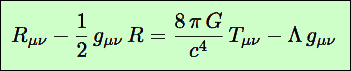
Si on place la constante cosmologique à gauche, elle prend un aspect géométrique, qui peut être utile dans certaines circonstances, mais c’est la première interprétation qui correspond aujourd’hui à la tendance en cosmologie (la tendance en cosmologie représente un courant majoritaire, étayé par des résultats expérimentaux et/ou théoriques. Ce n’est pas le seul désir de changer pour renouveler les stocks, comme dans d’autres domaines…).
Un trou noir correspond à la métrique de Schwarzschild, qui s’applique à sa symétrie sphérique, en l’absence de rotation puisque celle-ci modifie la symétrie. Le modèle qui décrit un trou noir en rotation est celui de Kerr, mais c’est une autre histoire.
Nous avons vu plus haut que la métrique de Schwarzschild est équivalente à celle de Minkowski, à grande distance (lorsque r est grand devant rs, donc lorsque 1 - rs / r vaut pratiquement 1). Mais près du trou noir, cette approximation n’est absolument plus valable. Une particule qui tombe vers le trou noir se trouve, à un instant t, à la distance r du trou noir, et r > rs (rayon de Schwarzschild de l’objet). Faisons donc tendre r vers rs par valeurs supérieures (r reste toujours plus grand que rs). Alors, rs / r tend vers 1 par valeurs inférieures. Le terme en dt2 de la métrique de Schwarzschild tend donc vers 0. Le dernier terme r2 (dθ2 + sin2θ dφ2) tend vers une valeur finie. Enfin, le terme médian
![]()
tend vers l’infini, puisque le dénominateur 1 - rs / r tend vers 0. Donc le ds2 tend vers l’infini.
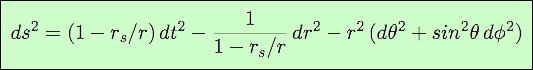
Par conséquent, l’intervalle entre deux événements tends vers l’infini. Ce qui veut dire que, vu de l’extérieur, ce qui se passe à la surface du trou noir est figé.
Une grande masse courbe l’espace-temps en son voisinage. La masse de la Terre est-elle suffisante pour que son effet soit mesurable ? La réponse est affirmative ! Le décalage spectral gravitationnel produit par la Terre est très faible, et des mesures très précises sont nécessaires pour le mettre en évidence.
Ceci a été fait en utilisant l’effet Mössbauer, qui produit une lumière de longueur d’onde très précise (une raie très fine). Cette précision a permis la mesure, et confirmé la prévision de la Relativité Générale.
La déviation des rayons lumineux a été confirmé dès l’éclipse totale de Soleil du 29 mai 1919. Une photo des étoiles visibles autour de la Lune cachant le Soleil a été prise. La comparaison avec une photo réalisée six mois auparavant, lorsque le Soleil était de l’autre côté du ciel, loin de ce champ d’étoiles, a montré que les étoiles paraissaient légèrement plus éloignées qu’en l’absence du Soleil. Les rayons étant déviés vers l’observateur, les images des étoiles sont écartées de leur position naturelle. Tout se passe comme si les rayons avaient traversé le verre d’une lentille convergeante. C’est ce qui justifie le nom que l’on donne maintenant à ces phénomènes.
La courbure des rayons lumineux est totalement inexplicable, et même inconcevable, dans la théorie Newtonienne. Puisque la masse m du photon est nulle, la force Newtonienne qu’il ressent F = G M m / r2 est strictement nulle. Mais en Relativité, la courbure de l’espace-temps n’a aucun rapport avec la lumière (on l’a vu dans la dérivation de la transformation de Lorentz) ; c’est une propriété de l’espace-temps lui-même, qui s’applique donc à tout ce qui s’y trouve, matière et lumière confondues.
Ce test a été une magnifique confirmation de la Relativité Générale, et en particulier du principe d’équivalence dont elle procède.
Depuis cette première observation, on a pu faire la même expérience en radio, en observant un quasar qui passe à proximité du soleil. La précision de la radiosatronomie atteignant la milliseconde d’arc, et l’effet étant de l’ordre de la seconde, on voit que la vérification est très précise.
En rdioastronomie, on peut même se payer le luxe de faire des mesures lorsque le soleil est loin du quasar : déplacement de 4 millisecondes d’arc à 90° du soleil ! Et enfin de 0,17 millisecondes d’arc à 175° du soleil, c’est-à-dire quasiment à l’opposé…
Depuis l’éclipse de Soleil de 1929, on a considéré de bien plus grandes masses : les objets produisant la déviation sont maintenant des galaxies, voire des amas de galaxies. Bien sûr, la distance est bien plus élevée, et les lumières déviées encore plus lointaines. Il y a une autre différence avec l’éclipse : la Terre tournant autour du Soleil en un an, six mois suffisent pour que le Soleil sorte de devant les objets déviés. Par contre, les galaxies et amas qui vont produire le même phénomène resteront pour une durée extrêmement longue (des millions, voire des milliards d’années) devant les mêmes lumières. Impossible donc de faire une différence entre deux photos avec et sans l’objet déflecteur.
Le premier exemple a été trouvé en 1979, lorsqu’on a montré que deux quasars distants de 5,7″ avaient exactement le même spectre. On en a conclu qu’il s’agissait de deux images du même objet. Beaucoup d’autres exemples ont été trouvés depuis.
La déviation des rayons lumineux est maximum si la source lumineuse et la masse sont alignées avec la Terre (avec l’observateur). Dans ce cas, il y a symétrie autour de l’axe de visée, et selon la distance entre la source et la masse, on observera un simple point lumineux amplifié (puisque tous les rayons émis dans un cône convergent vers l’observateur), ou bien un anneau lumineux. Ces deux cas se produisent, bien que rarement.
Lorsque les conditions de distance et/ou d’alignement ne sont pas parfaitement remplies, on observe des sortes d’aberrations, comme les aberrations optiques. On voit alors des arcs lumineux (image d’une galaxie lointaine), des points multiples (croix d’Einstein), ou simplement des déformations de l’image d’une galaxie.
On peut aussi avoir ce phénomène avec des masses bien plus faibles, et des objets plus proches. Par exemple si une naine brune (un centième de la masse du Soleil) passe devant une étoile de la Galaxie. Cette idée a été exploitée pour dénombrer les naines brunes existant dans la Voie Lactée. On nomme de dernier phénomène micro lentille gravitationnelle.
L’analogie avec une lentille de verre convergeante justife le nom de lentille gravitationnelle. Aujourd’hui d’observation courante, les lentilles gravitationnelles sont une précieuse source de renseignements dans de nombreux domaines. En particulier, elles permettent de d’évaluer la masse des objets qui les produisent, qu’ils soient visibles ou non…


Cette image montre la Croix d’Einstein, nommée ainsi parce que la Relativité Générale explique ce que l’on voit. Les quatre points extérieurs sont des images d’un même quasar, située derrière l’objet central, qui est une galaxie servant de lentille gravitationnelle. Le très bon alignement, dû au hasard, entre les deux objets, permet la formation de ce mirage. Ces phénomènes optiques sont de magnifiques confirmations des idées d’Einstein qui ont fondé la Relativité Générale. La distance angulaire entre les deux images en haut et en bas est de seulement 1,6 secondes d’arc. L’image a été prise par la camera FOC (Faint Object Camera) de l’Agence Spatiale Européenne, à bord du télescope spatial.
La résolution de l’équation d’Einstein permet de mettre en évidence des défomations périodiques de l’espace-temps produites par le déplacement des masses (exactement comme la déplacement des charges électriques produit des déformations du champ électromagnétique, c’est-à-dire des ondes électromagnétiques). On en déduit que les masses en mouvement produisent des ondes gravitationnelles.
Le problème vient de la différence énorme entre l’intensité des deux interactions que l’on vient de citer. La gravitation est 1038 fois plus faible que l’interaction électromagnétique. Aussi, l’énergie transportée par les ondes gravitionnelles est-elle plus faible dans les mêmes proportions. Et c’est tant mieux pour nous, car si elles avaient la même intensité, les tremblements de terre les plus violents ne seraient, en comparaison, que de douces plaisanteries (et ils ne le sont malheureusement pas).
Dans ces conditions, la détection des ondes gravitationnelles est un problème très sérieux, non encore résolu. Des instruments volumineux ont été construits dans ce but (VIRGO, LIGO), mais ils n’ont toujours pas la sensibilité suffisante pour espérer détecter des petits phénomènes courants. Ils ne pourraient détecter, à la rigueur, que des effondrement d’une étoile massive en trou noir à courte distance, ou la fusion de deux trous noirs.
A ce propos, il n’est pas question d’envisager que deux trous noirs se rencontrent par hasard et fusionnent ; la probabilité est bien trop faible. Pour que deux trous noirs fusionnent, il faut qu’ils soient déjà proches l’un de l’autre, c’est-à-dire en orbite commune. Un tel couple peut résulter de l’effondrement de deux étoiles déjà associées et assez massives pour suivre un tel destin.
Le 14 septembre 2015, ceci a été confirmé par l’observation de la fusion de deux trous noirs, de 29 et 36 M respectivement. Leur fusion a donné un nouveau trou noir de 62 M. Les 3 M qui manquent ont été dissipées sous forme d’énergie gravitationnelle ! C’est une confirmation de plus de la Relativité Générale.
Dans une situation proche, on avait découvert un couple d’étoiles à neutrons, dont l’un des membres est un pulsar. Le couple est nommé pulsar binaire. Il est nommé PSR 1913+16. Les deux objets sont compacts, et tournent à une distance très faible l’un de l’autre, de l’ordre de 3 R (soit un peu plus de 2 millions de kilomètres). L’excentricité est de 0,66, et l ’orbite est parcourue en moins de 8 heures. Dans ce ballet infernal, selon la Relativité Générale, les deux étoiles doivent rayonner des ondes gravitationnelles, mais le calcul montre qu’elles sont encore indétectables avec les instruments actuels.
Cependant, la production de ces ondes entraîne une perte d’énergie du couple. D’où provient l’énergie rayonnée ? La seule possibilité est l’énergie potentielle des deux étoiles, qui définit leur distance. Perdant de l’énergie, elles se rapprochent inexorablement l’une de l’autre. Or la période des pulsations d’un pulsar est extrêmement précise (elle provient de sa rotation sur lui-même). Et puisque l’orbite est très excentrique, il y a de grandes variations de vitesse entre le périastre et l’apoastre. Donc, un décalage Doppler différent entre ces deux points. La mesure de ce décalage variable a permi de remonter aux paramètres orbitaux, et de connaître précisément les masses des deux objets (de l’ordre de 1,4 M). Enfin, les observations prolongées font apparaître une diminution de la période orbitale, en parfait accord avec celui prévu par la Relativité Générale.
Ainsi, le pulsar binaire nous a donné l’opportunité de vérifier pour la première fois cette théorie dans l’une de ses prévisions les plus subtiles. Nous en avons maintenant une vérification directe, pour des objets très massifs.
Plus récemment, en 2003, on a découvert un pulsar double (les deux composantes sont des pulsars) à 1.600 AL de la Terre, et nommé PSR J0737-3039. Cet objet a permi une confirmation encore bien plus précise de la théorie. En plus, des chercheurs toulousains pensent que ce couple pourrait donner une première preuve de l’existence d’une énergie du vide. Mais les instruments disponibles aujourd’hui ne sont, là encore, pas assez sensibles…
Josef Lense et Hans Thirring, astronomes autrichiens, ont découvert en 1918 une conséquence de la Relativité Générale, qui s’observe lorsque l’objet qui produit la gravité est en rotation. Il se traduit par un entraînement de l’espace-temps par la rotation, qui en retour va modifier les géodésiques autour de l’objet. Mais cet effet est extrêmement faible, et aucune vérification n’a pu être réussie à ce jour. La sonde américaine Gravity Probe B (NASA) a été lancée en 2005, et a terminé son programme d’observations. Les données recueillies ont été traitées, mais présentent un bruit non prévu qui perturbe fortement leur interprétation. Ce bruit fait passer la précision des mesures des 1 % prévus à quelques 10 ou 20 %. Cependant, les deux phénomènes analysés ont été vérifiés, avec cette précision dégradée.