Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Variables pulsantes | |||||||
Les périodes sont comprises entre quelques heures et 100 jours. On distingue deux groupes, en fonction de la période :
Ces étoiles présentent toutes une courbe de lumière avec une montée de la luminosité assez rapide, et une descente nettement plus lente. La variation de luminosité est de l’ordre d’une magnitude, donc relativement faible (leur luminosité correspondante est tout de même 2,5 fois plus forte au maximum qu’au minimum).
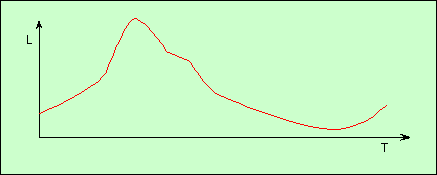
Ce groupe à courte période comprend 3 types d’étoiles :
Les variations lumineuses s’accompagnent de variations :
Leur luminosité est très forte, puisque leur magnitude absolue atteint M = - 6 (10.000 fois la luminosité du Soleil) .
Ce sont des étoiles jeunes (de population I). On les observe essentiellement dans le plan de la Voie Lactée.
Aucune Céphéide ne se trouve à moins de 200 AL, limite de la méthode des parallaxes, par les moyens d’observation traditionnels depuis le sol. Le satellite européen Hipparcos a permi récemment de franchir cette limite. Avec leur luminosité, elles sont visibles jusqu’à 100 millions d’années-lumière !
Hipparcos (HIgh Precision PARallax COllecting Satellite, ESA) a révolutionné l’astrométrie, en mesurant la position de 100.000 étoiles avec une précision de 0,001 seconde d'arc ! soit 100 fois mieux que ce dont on disposait avant. Cette précision a entraîné une révision de toutes les mesures dans l’univers, car leur base commune était sous-estimée.
Gaia (Global Astrometric Interferometer for Astrophysics, ESA) est le successeur d’Hipparcos. Sa précision est extraordinaire : 7 micro arcsecondes pour les étoiles jusqu’à la magnitude visuelle 10 ;
jusqu’à la magnitude limite de 20, la précision décroît pour atteindre 300 micor arcsecondes au minimum.
Sa carte d’identité :
La régularité des variations des Céphéides se traduit par une relation entre leur période et leur luminosité. Cette relation a été découverte par Miss Henrietta Leavitt en 1912. Elle indique que la luminosité absolue de ces étoiles augmente avec leur période : les plus lentes sont les plus lumineuses. Miss Leavitt étudiait les variables du Grand Nuage de Magellan. Cette galaxie proche, satellite de la nôtre, est de petites dimensions par rapport à sa distance. Aussi, on peut considérer que toutes ses étoiles sont à peu près à la même distance de nous : d = cste (constante). Par conséquent, 5 log d - 5 = cste ; et par suite :
m - M = 5 log d - 5 = cste
d’où : M = m - cste
Par conséquent, leur magnitude apparente m, diffère de leur magnitude absolue M d’un facteur constant, le même pour toutes. Elle a pu ainsi étudier la luminosité des étoiles en fonction de leur période P, et en déduire la relation :
M = -3,10 log P + 1,70 (B - V) + cste
Dans cette relation, le terme B - V exprime la couleur de l’étoile. B est sa magnitude apparente dans le bleu, et V sa magnitude apparente dans le visible (plus centré sur le jaune). Pour une étoile blanche, la luminosité est la même dans les deux cas, donc B - V = 0. Plus le terme B - V est important, plus l’étoile est colorée. Au lieu de ne mesurer que la magnitude globale, on utilise deux filtres, qui donnent respectivement B et V. On remarque que la différence B - V est indépendante de la distance de l’étoile.
La relation a été calibrée sur les Céphéides proches, dont on connait la distance (par la méthode géométrique des parallaxes) et par conséquent la luminosité, donc la magnitude absolue M. On en déduit la constante, et la relation devient :
M = -3,10 log P + 1,70 (B - V) - 2,37
Enfin, les Céphéides sont des supergéantes, très lumineuses, donc visibles de très loin : le télescope spatial a permi d’en observer une à 5 méga parsecs, i.e. à 15 millions d’années-lumière.
Réciproquement, si on observe P et B - V pour une céphéide quelconque, on en déduit M. En mesurant de plus m (ou plus précisément B et V), on en déduit la distance d. Cette relation est à la base de la détermination des distances dans l’Univers.
Une analogie peut expliquer cette méthode. Construisons des guirlandes de Noël clignotantes avec les caractéristiques suivantes :
Vous admirez la ville, toute illuminée, et vous aimeriez savoir où se trouve telle guirlande. Vous observez la rapidité de son clignotement : par exemple un éclair toutes les 100 secondes ; vous en déduisez que ses ampoules font 100 W. Et comme elles vous semblent très faibles, vous comprenez qu’elles sont très loin.
Vous voyez une autre guirlande, qui clignote en 25 secondes, et apparaît aussi brillante. Ses ampoules de 25 W étant 4 fois moins lumineuses, vous en déduisez qu’elle sont 41/2 = 2 fois plus près. Si vous pouvez déterminer la distance de la guirlande la plus faible, vous en déduirez celle de la plus lointaine.
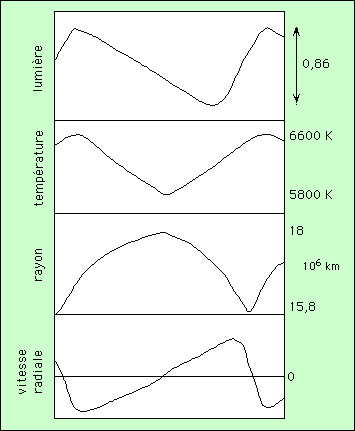
La relation Période-Luminosité des Céphéides provient de variations de leur diamètre, donc de surface : l’étoile grossit et maigrit périodiquement. La lumière qu’on en reçoit étant proportionnelle à la surface, et celle-ci variant avec la période, il est normal que la luminosité varie avec la période (le phénomène est un peu plus complexe, car la température superficielle varie aussi). L’évolution dans le temps des courbes caractéristiques, comme celles de δ Céphée données plus haut, le montre :
Les variations de luminosité des Céphéides ne proviennent pas d’explosions : il n’y a pas d’ondes de choc, mais seulement la propagation d’une onde sonore. Dans le mode fondamental, la période de l’onde est :
P = 0,05 × R3/2 × M-1/2
Cette onde est une onde sonore. Le mode fondamental est celui de plus basse fréquence, et de plus grande amplitude. Les autres sont ses harmoniques, à l’instar de ceux qui donnent de la couleur à un instrument de musique. On comprendra donc que la fréquence de ce mode soit lié à la géométrie de l’étoile, comme la fréquence d’une corde de violon est fonction de sa longeur et de sa tension.
La masse de l’étoile est le produit de sa masse volumique moyenne ρ, par son volume :
M = ρ V
Le rayon de l’étoile étant R, le volume s’écrit :
V = 4/3 π R3
Donc la masse est :
M = ρ V = ρ 4/3 π R3
En reportant cette expression dans celle de la période on obtient :
P = 0,05 × R3/2 × (ρ 4/3 π R3)-1/2
et après simplification :
Puisque la période, multipliée par ρ1/2 (la racine carrée de ρ) donne le même résultat pour toutes les céphéides, si ρ diminue, P doit augmenter. Les supergéantes qui ont une densité faible, ont donc une période longue.
La masse (donc aussi la densité) et le rayon étant reliés à la luminosité, c’est l’explication de la relation période-luminosité.
L’explication des pulsations a longtemps défié les astronomes. Eddington a compris qu’il devait y avoir un mécanisme qui retient l’énergie, mais l’opinion commune était que les RR Lyræ étaient des étoiles doubles dont le compagnon, invisible, était l’élément perturbateur. Eddington a insisté, et développé une théorie montrant qu’un mécanisme bloquant l’énergie devait être à l’œuvre. L’avenir lui a donné raison, mais encore fallait-il trouver ce mécanisme.
Les pulsations résultent de la transformation d’une énergie quelconque en énergie mécanique. L’énergie nucléaire centrale ne joue aucun rôle : les conditions physiques dans le cœur de l’étoile ne varient pas, seules les couches extérieures pulsent.
Les variations de température sont produites dans l’atmosphère par une modulation de sa transparence. Il s’ensuit une variation du flot d’énergie à travers les couches.
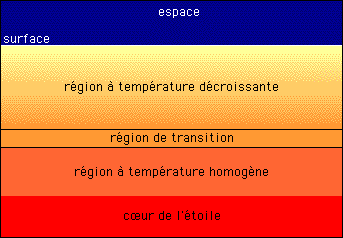
Lorsque l’atmosphère de l’étoile se contracte, sa température devrait augmenter. Mais l’énergie gravitationnelle libérée est aussitôt utilisée pour ioniser une couche d’hélium (elle sert à ioniser les atomes, donc elle ne peut pas augmenter la température). La couche ne s’échauffe donc pas en se contractant.
L’opacité de l’atmosphère est fonction de sa densité ρ et de sa température T :
κ mesure l’opacité. L’étoile est d’autant plus opaque qu’elle est plus dense, puisqu’il y a davantage de matière susceptible d’arrêter le rayonnement ; si la température augmente, la vitesse des atomes augmente, et leurs interactions avec les photons diminuent, donc ils en arrêtent moins.
Dans une atmosphère stellaire normale, n vaut 1, et s est de l’ordre de 3,5. Lorsqu’une étoile normale se contracte, ρ augmente, et T aussi. Mais le cube de T croît plus vite que ρ, et l’opacité diminue, donc l’énergie supplémentaire peut s’échapper.
Seulement, une Céphéide n’est pas une étoile normale : dans la relation de Rosseland, la valeur de s peut devenir nulle ou même négative. L’ionisation empêche l’augmentation de température, ce qui fait que ρ l’emporte.
Ainsi, lorsque la Céphéide se contracte, sa densité augmente à température relativement constante, et donc l’opacité de l’atmosphère augmente aussi.
L’énergie produite dans le cœur se trouve alors piégée par cette couche, et bientôt provoque la dilatation !
Lorsque la dilatation commence, le phénomène inverse se produit, les noyaux atomiques se recombinent avec les électrons, l’atmosphère redevient transparente. Alors, les rayonnements peuvent s’échapper, ce qui entraîne un refroidissement… qui va produire une nouvelle contraction !
Le piégeage de l’énergie est comparable à celui qui se produit dans une serre.
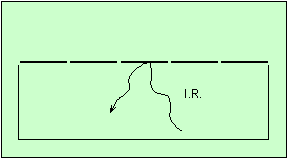 |
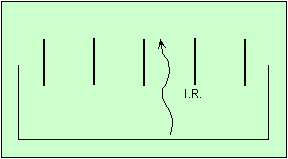 |
Le schéma de gauche montre une serre fermée. Le sol rayonne de l’infrarouge, et se refroidit. Mais les infrarouges sont réfléchis par le verre, qui est opaque pour eux. Ils sont donc renvoyés vers le sol qu’ils réchauffent.
Si les vitres sont ouvertes, comme dans l’illustration de droite, les infrarouges peuvent s’échapper, et le sol se refroidit vraiment.
En infrarouge, la photométrie des Céphéides dépend de leur diamètre, alors que dans le visible la température effective est le paramètre principal.
Pour comprendre ce mécanisme, on peut utiliser une analogie. Une cocotte en fonte pleine d’eau est mise sur le feu. On pose le couvercle. Au moment où on le dépose, la pression à l’intérieur de la casserole est égale à la pression extérieure. Le couvercle va jouer un rôle similaire à celui de l’atmosphère opaque de la Céphéide, en empêchant l’évacuation de l’énergie ; la chaleur du gaz brulé par la cuisinière sera analogue à celle produite par les réactions nucléaires du cœur de l’étoile.
Le dégagement de vapeur d’eau à l’ébullition va faire monter la pression à l’intérieur. Tant que celle-ci est inférieure au poids du couvercle, la casserole restera fermée et la vapeur ne pourra pas s’en échapper. La pression monte donc toujours. Viendra un moment où elle sera suffisante pour équilibrer le poids du couvercle ; à ce moment-là, une petite augmentation de pression va soulever le couvercle, laissant la vapeur s’échapper librement, et donc la pression retomber brutalement. Par suite, le couvercle retombe, la pression dans la casserole est à nouveau égale à la pression extérieure, mais va tout de suite commencer à augmenter, jusqu’à équilibrer le poids du couvercle…
Ceci est un exemple quotidien de phénomène non linéaire. Un phénomène est dit linéaire si à un doublement d’un paramètre correspond également le doublement d’un autre ; le déplacement d’un train est un phénomène linéaire (à vitesse constante) : en deux fois plus de temps, il va deux fois plus loin. A la fontaine, il faut deux fois plus de temps pour remplir deux seaux d’eau que pour en remplir un seul.
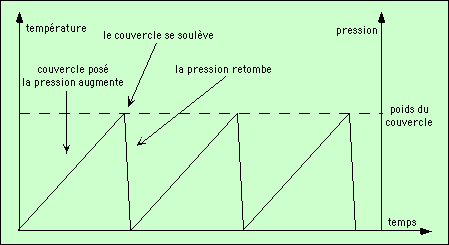
Dans notre casserole, le phénomène serait linéaire si le doublement de la pression à l’intérieur correspondait à un doublement de la perte de vapeur par le couvercle. Ce n’est pas le cas, la perte est quasi nulle tant que le poids du couvercle est supérieur à la pression de la vapeur qui le pousse. Lorsque la pression devient trop forte, le couvercle se soulève d’un coup ; toute la vapeur s’échappe et la pression retombe brusquement. Alors, n’étant plus soutenu, le couvercle retombe et rebouche la casserole ; la pression recommence alors à monter…
Parmi les variables pulsantes, qui présentent un mécanisme semblable, on trouve les δ Scuti qui sont de période très courte et bleues, et les β Canis Majoris qui sont plus brillantes, en rotation rapide.
Les Céphéides classiques sont des étoiles de population I (donc assez jeunes).
Les résultats ci-dessus ont été obtenus avec des moyens traditionnels, des télescopes classiques. On fait maintenant des observations avec des interféromètres, en particulier avec le VLTI (instruments MIDI et VINCI). C’est ainsi qu’on a observé en 2006 la céphéide L Car, dans l’hémisphère sud.
Précisons tout d’abord que la détermination de la relation Période-Luminosité est calibrée (détermination du zéro) par la méthode BW (Baade-Wesselink, 1926, 1946). Elle consiste à déterminer simultanément les variations des dimensions angulaires et linéaires pour déduire la distance de l’étoile. En effet, toutes les céphéides sont lointaines, et non accessibles à une mesure parallactique. Pour déterminer les dimensions linéaires de l’étoile, on intègre les variations de vitesses radiales, ce qui donne une valeur assez fiable. Les dimensions angulaires étaient mesurées indirectement par photométrie, en supposant que l’étoile est un corps noir parfait. Mais aujourd’hui, on peut les mesurer directement par interférométrie.
La méthode BW classique fait l’hypothèse que l’étoile est nue, non entourée d’un nuage de gaz et poussières. Or cette hypothèse est fausse au moins dans le cas de L Car, la céphéide la plus brillante dans le ciel. Celle-ci est une supergéante jaune qui se trouve à 1.850 AL de la Terre, et sa masse atteint 13 M. Sa période est de 35,5 jours. On observe une raie Hα non pulsante, qui doit être émise par une enveloppe. Le taux de perte de masse, responsable de l’enveloppe, atteindrait 10-5 M / an. D’ailleurs, une émission de OI se voit à plusieurs secondes d’arc de l’étoile.
Près de son maximum (visible), L Car a une Teff de 5.500 K.
La comparaison de perte de masse entre différentes céphéides a donné une indication : le taux de perte de masse serait plus important pour les céphéides à longue période que pour celle à courte période.
Observées en infrarouge, les céphéides montrent souvent un excès de brillance, provenant d’une enveloppe. Un tel excès de rayonnement dans l’infrarouge (F(60 µm) / F(12 µm)) moyen est caractéristique d’une enveloppe chaude, poussiéreuse. Mais cet excès dépend de la température de l’enveloppe, et n’est pas toujours détectable.
Avant 2006, RS Pup était la seule Céphéide connue pour être associée à une enveloppe circumstellaire.
On les appelait autrefois variables d’amas, parce qu’elles sont abondantes dans les amas globulaires et le bulbe galactique.
RR Lyræ :
Caractéristiques des étoiles de type RR Lyræ :
Les RR Lyræ sont sur la branche horizontale, à l’intérieur de la bande d’instabilité. Provenant de la Séquence Principale, elles ont gravi la branche des Géantes Rouges, subi le flash de l’hélium, puis ont atteint la Branche Horizontale. Là, elles sont arrivées dans la zone d’instabilité où elles subissent les pulsations. Leur position dans cette bande du diagramme HR montre que leur température effective est comprise entre 6.100 K et 7.400 K. Ce sont donc des étoiles un peu plus chaudes que le Soleil.
Leur métallicité est faible, comprise entre 10-4 et 10-2 (la métallicité du Soleil est de 2 10-2).
On subdivise les RR Lyræ en deux sous-classes :
| RRab | La montée de lumière est très rapide. La descente est rapide, mais moins. La luminosité est pratiquement constante pendant une demi-période au minimum (malgré de légère variations). L’amplitude de variation est entre 1,3 et 0,9 magnitudes. La période est comprise entre 12 et 15 heures. |
| RRc | La luminosité change tout le temps, et assez lentement. L’amplitude est de l’ordre d’une demi-magnitude. La période de 8 à 10 heures. |
Le nom RRab s’explique par des raisons historiques. Bailey a créé trois classes, a, b et c. Puis on a montré que les classes a et b étaient trop semblables pour les distinguer. Les courbes de lumière typiques sont :
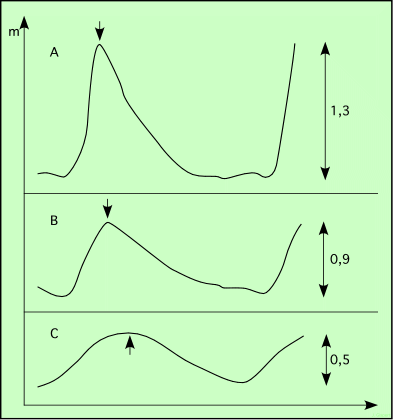
Déterminer la masse des RR Lyræ n’est pas chose facile, car on n’en connait pas de double. Ceci est très surprenant a priori. Mais l’explication est assez simple. Supposons qu’un couple d’étoiles se forme, et commence son évolution. Selon leurs masses, les deux étoiles vont évoluer plus ou moins vite. Considérons d’abord le cas où le compagnon est plus massif que la future RR Lyræ. Il va évoluer plus rapidement. Or la RR Lyræ est déjà une étoile vieille ; par conséquent, le compagnon plus massif a déjà évolué vers le stade naine blanche ou même étoile à neutrons selon sa masse. Or ces deux types d’étoiles sont de très faible éclat, et difficiles à détecter. Prenons maintenant le cas où le compagnon est moins massif. Les RR Lyræ ayant une masse de l’ordre de 0,7 M, le compagnon moins massif est une naine rouge, de faible éclat encore.
Par conséquent, que le compagnon soit plus ou moins massif, son éclat est sûrement faible, ce qui explique qu’on ne connaisse pas avec certitude de RR Lyræ en couple. Pour les étoiles de masse moyenne, on considère que 50 % à peu près sont dans un système au moins binaire. Il doit en être de même pour les RR Lyræ. C’est donc un bais observationnel qui empêche d’en découvrir pour l’instant.
La masse d’une RR Lyræ est très concentrée. Le diamètre de l’étoile est compris entre 4 et 6 fois celui du Soleil. On considère que le cœur a un diamètre de l’ordre de 5 fois celui de la Terre (70.000 km). Il représente donc seulement 1 % du diamètre de l’étoile, et pourtant contient la quasi totalité de la masse : 0,5 M. L’enveloppe, qui occupe presque tout le volume de l’étoile, ne représente que 0,001 M.
La loi de Ritter est valable pour les RR Lyræ.
Si P est donnée en jours, et ρ en densité solaire, alors la constante vaut 0,04 pour toutes les RR Lyræ de sous-type ab.
Les RR Lyræ ont été découvertes et étudiées initialement dans les amas globulaires, mais on en a découvert beaucoup dans le disque galactique. On en connait aujourd’hui 7.000 dans ce disque.
W Virginis a été découverte par Schönfeld en 1866. Sa courbe de lumière ne présente pas la même forme que celles des Céphéides classiques.
W Virginis :
Ce sont des Céphéides de population II, vieilles. Elles sont situées dans le halo galactique, et dans les amas globulaires. Leur courbe de lumière est d’allure différente ; elles montrent d’intenses raies du calcium ionisé en émission. Leurs périodes sont soit inférieures à 2,5 jours, soit supérieures à 10 jours. Enfin, leur amplitude est souvent supérieure à 1 magnitude.
La bande d’instabilité est une bande presque verticale, dans le diagramme HR :
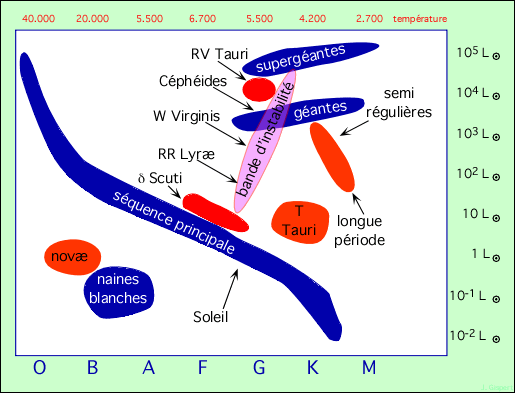
Elle indique la place des étoiles variables pulsantes radiales. Comment explique-t-on que, de part et d’autre, il n’y ait pas de pulsations ?
Par le fait que la bande d’instabilité correspond aux températures qui permettent l’ionisation de l’hélium, et accessoirement de l’hydrogène. Du côté rouge de la bande (étoiles de plus faible masse), la convection peut se développer et bloquer les pulsations. Du côté bleu au contraire, la zone de seconde ionisation de l’hélium est à une altitude plus élevée, où la densité est plus faible. L’augmentation d’opacité produite ne suffit pas, dans ce milieu dilué, à arrêter la lumière, et donc ne bloque pas l’énergie.
Mira Ceti est la première découverte, par Fabricius en 1596. Sa période moyenne est de 331 jours 15 heures, avec des valeurs extrêmes observées de 310 et 370 jours. Ce n’est donc pas une variable très régulière. Au maximum, sa magnitude vaut de 2 à 5, et au minimum de 8,3 à 10,1. C’est une étoile très brillante, dont la magnitude absolue est - 2. C’est aussi une supergéante, car son diamètre dépasse 4 unités astronomiques : plus de 4 fois la distance Terre-Soleil ! Si on représente le Soleil par une tête d’épingle en verre, Mira est représentée par un ballon de 42 centimètres de diamètre…
Le cas de Mira est un peu particulier, et ses caractéristiques perturbées par le fait qu’elle est double, et peut-être triple. Mais la variation ne provient pas de la duplicité.
Le spectre du compagnon est Beq (étoile chaude à raies d’émission), et c’est une variable de type P Cygni. Elle varie de 9,6 à 12,0.
Les variables de type Mira ont une période de plus de 50 jours, et des variations d’éclat de 2,5 à 6 magnitudes (donc une variation de luminosité de 10 à 250 fois). Les plus lentes ont une amplitude de variation plus importante.
Leur type spectral est M, C ou S ; M est très fréquent. Celles de type S sont très jeunes, elles appartiennent au disque galactique et sont de population I.
Elles présentent des raies d’émission intenses, en particulier de l’hydrogène (d’où un type spectral Me). Elles sont de classe de luminosité II ou III (géantes brillantes ou géantes).
On a essayé de définir une relation période-luminosité pour ces étoiles, mais elle est mal définie.
La cause des variations est inconnue ; elles sont pulsantes, mais les pulsations ne suffisent pas à expliquer l’amplitude des variations.
Les Céphéides et les Miras montrent des pulsations régulières et de grande amplitude, dont la vitesse est de quelques dizaine de km s-1 Les pulsations amènent de la matière à une hauteur suffisante pour permettre la condensation de poussières, et entraîner une perte de masse. La perte de masse dans les géantes rouge serait due à des ondes sonores produites par les mouvements dans les grandes cellules de convection. Les Céphéides étant des supergéantes qui pulsent, pourraient perdre de la masse par les deux mécanismes, pulsation et convection.
On note des similitudes entre les supergéantes rouges Bételgeuse et μ Cep, et les étoiles de type Mira. Dans l’atmosphère, à 2 R* pour les Miras, et à 1,4 R* pour les supergéantes rouges, on observe une couche chaude moléculaire, contenant H2O et CO. Les températures sont de l’ordre de 2.000 K. Bételgeuse contient même du corindon (Al2O3), qui serait ainsi une base pour la formation des poussières silicatées.
Davantage de détails concernant les variables de type Mira se trouvent ici.
Les étoiles de type RV Tauri (RV Tauri elle-même en étant le prototype), sont :
Les Variables semi-régulières sont des étoiles pulsantes rouges, dont la courbe de lumière est plus complexe que celle des variables à longue période.
Leur amplitude n’excéde pas 2 magnitudes. Elles montrent des variations irrégulières, avec un cycle plus ou moins évident.
| type d’étoile | période (jours) | amplitude lumière | amplitude vitesse (km/s) | magnitude absolue visuelle | type spectral |
|---|---|---|---|---|---|
| Céphéides | 1 | 0,1 à 2 | 5 à 60 | 0 à -5 | F6 à K2 |
| RR Lyræ | 0,2 à 1 | 0,3 à 2 | 20 à 100 | 0,5 à 0 | A2 à F6 |
| δ Scuti | 0,02 à 0,3 | 0,01 à 0,3 | 10 à 100 | 3 à 0 | A2 à F2 |
| ZZ Ceti | 10-3 à 10-2 | 0,3 | .. | 8 à 10 | DA |
| RV Tauri | 30 à 150 | 3 à 4 | 20 à 30 | +1 à -2 | M, R, N, S |
| variables rouges | 30 à 1000 | 0,5 à 11 | 20 à 30 | +1 à -2 | M, R, N, S |
| β Canis Majoris | 0,1 à 0,3 | 0,02 à 0,25 | 5 à 150 | -5 à -3 | B0 à B3 |
| Variables B | > 0,02 | 0,01 à 0,06 | 5 à 30 | -8 à -2 | O9 à B7 |
Suite : variables explosives
---=OO=---