Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Relativité Galiléenne | |||||||
Eppur, si muove !
Galilée
Table des matières
1.1 Le navire et la pierre
1.2 Observateurs galiléens et équivalence
1.3 Référentiel
1.4 Relativité du mouvement uniforme
1.5 Principe d’inertie
2 Problème fondamental
2.1 Transformation de Galilée (changement de référentiel)
2.2 Réponse galiléenne : addition des vitesses
2.3 Le temps
2.4 Que sont l’espace et le temps ?
2.5 La dynamique
2.6 Electromagnétisme
3 Résumé
La Physique est la science qui vise à représenter et expliquer le fonctionnement de la Nature. Elle consiste à écrire des lois sensées représenter ce fonctionnement. Si c’est le cas, ces lois nous permettent de répondre aux différentes questions que l’on peut se poser à propos de tout phénomène.
Un physicien opère dans son laboratoire, y fait des expériences. De leur résultat, il infère les lois qui régissent les objets étudiés. Il est évident que cette approche est limitative par rapport au problème posé ci-dessus, puisque le champ de l’expérience n’est qu’une toute petite partie de la Nature ! On imagine donc que toute théorie bâtie de cette manière aura une portée limitée au domaine dans lequel les expériences la valident.
Mais le rêve de bâtir une Physique a-t-il un sens ? Autrement dit, existe-il des lois générales qui régissent la Nature ?
Ceci étant, il faut étudier comment les corps tombent, à quelles lois ils obéissent. Et ce problème est loin d’être simple. Galilée a joué un grand rôle dans sa résolution.
La première chose à comprendre pour la chute des corps, est l’indépendance de la matière. Ceci est loin d’être évident : lorsque les feuilles tombent à l’automne, on aime bien regarder leur chute lente et tourbillonante, qui est reposante pour l’esprit. Par contre, l’expérience de tous les jours nous montre qu’un objet compact, comme une pierre, tombe brutalement. Nos sens nous indiquent donc que la chute se fait selon la nature de l’objet qui tombe. Mais ceci n’est qu’une illusion, et il revient à Galilée de l’avoir compris, et d’avoir fait une expérience célèbre pour le montrer : il lâcha deux objets de nature différente du haut dela tour de Pise, et tout le monde pût constater que les deux arrivèrent au sol en même temps. Mais Galilée utilisa deux objets compacts, l’un plus lourd que l’autre. Il n’aurait pas pu utiliser une plume pour son expérience : celle-ci, dans sa chute, offre une grande surface à l’air qu’elle traverse, et l’écoulement de l’air autour d’elle la freine. Cet écoulement étant de plus turbulent, elle oscille.
Des physiciens ont fait cette expérience, bien après Galilée, dans une cloche à vide : l’air étant retiré, la plume n’a plus de support, et peut tomber librement. Mais la plus belle réalisation a été faite le 2 août 1971 par Dave Scott, sur la Lune :
Le résultat est ici parfaitement visible : la plume tombe exactement comme le marteau dans le vide lunaire, et la nature du corps ne change pas sa réponse à une accélération.
Un autre problème important se pose : les lois sont-elles les mêmes si on fait les expériences dans un mobile ? Si elles n’avaient pas de lien, la Physique n’aurait guère de sens. D’innombrables phénomènes produisant un mouvement, la question est très importante.
Une expérience illustre cette question :
Considérons un navire au port, et la vigie qui lâche une pierre du sommet du mât. Vous imaginez bien que la pierre tombe au pied du mât.
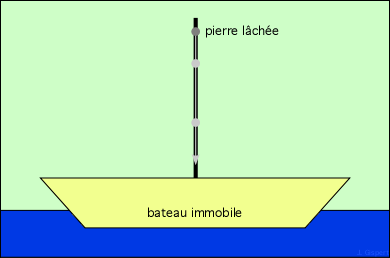
Si la vigie lance la pierre vers l’avant, le bateau étant toujours immobile, la pierre tombera sur le pont un peu en avant du mât :
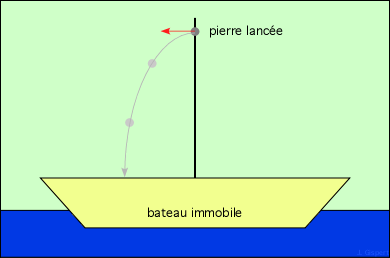
Maintenant, le navire est en haute mer, porté par un bon vent, et file à vitesse constante (mouvement rectiligne uniforme). Que fera la pierre, si la vigie répète son expérience dans ces nouvelles conditions, en lâchant la pierre sans la lancer ? (on suppose une mer d’huile, le navire restant parfaitement horizontal dans les deux cas). La réponse à cette question n’est pas si évidente. Bien des débats ont eu lieu à son sujet. Mais en fait, la pierre tombe toujours au pied du mât :
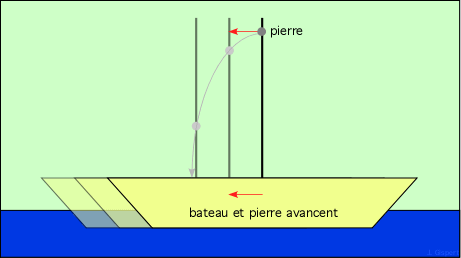
On pourrait imaginer qu’elle tombe en arrière, puisque la navire avance pendant la chute. Mais la pierre aussi avance, puisqu’avant de tomber, elle était portée par le bateau à la même vitesse que lui. Pendant sa chute, elle continue d’avancer par inertie, à la même vitesse que le bateau, et donc tombe au même endroit que lorsque le bateau était immobile.
On peut dire aussi que, vue du bateau, la pierre n’a pas de mouvement horizontal par rapport au bateau, même si le bateau avance ! Donc elle tombe bien au pied du mât.
On peut sans doute comprendre mieux tout ceci si on suppose que le bateau passe sous un pont (navigation fluviale). Et lorsque le bateau passe, quelqu’un lâche une pierre du pont au même moment que la vigie au sommet du mât. Les deux pierres sont soumises à la même force de gravitation, et donc leur mouvement vertical est le même. Mais celle qui est lâchée du pont n’a pas de vitesse horizontale, et tombe donc d’un mouvement vertical pur. Par contre, celle qui est lâchée du mât possède, au moment où commence sa chute, une vitesse horizontale identique à celle du bateau. Aussi conserve-t-elle cette vitesse par inertie. Elle est donc animée de deux mouvements, et suit une trajectoire qui les combine. L’animation ci-dessous le montre :
img src="RGal_img/navire.gif">��
Il y a deux choses à retenir de cela :
Il faut donc admettre que l’on puisse décrire différemment UN MEME PHENOMENE, selon le point de vue d’où on l’observe. En termes plus techniques, on dira que les mesures de position que l’on fait de la pierre dépendent de la situation de l’observateur !
Ce sont les conséquences de ces points de vue différents qui constituent la Relativité Galiléenne.
Précisons encore un peu cela : vu du quai, la trajectoire de la pierre est une parabole, vue du bateau elle est rectiligne. Mais si on projete la parabole sur un axe vertical, autrement dit si on annule le mouvement horizontal de la pierre, on retrouve exactement le mouvement de la pierre vu du bateau. Cette annulation du mouvement du bateau peut se faire si l’observateur qui est sur le quai marche dans la même direction et à la même vitesse que le bateau. Il voit alors le bateau immobile, et la pierre tomber verticalement au pied du mât.
Cette remarque nous indique que, même si les histoires racontées par deux personnes sur un même phénomène peuvent différer, on peut envisager un moyen de transformer l’une en l’autre, et donc de réduire ces différentes histoires à une seule qui représente le phénomène lorsqu’on ne se déplace pas par rapport à lui. Dans la suite, nous allons préciser tout cela. Puisque la différence est une question de point de vue, lepromeneur sur le quai peut changer de point de vue en marchant à la même vitesse que le bateau.
On utilise le terme observateur au lieu de expérimentateur. Le second a un sens actif, le premier est passif. Cependant on considère que, même lorsqu’on monte une expérience, on est passif pendant son déroulement, et on observe ce qu’il se passe.
On s’intéresse à la Mécanique : la Mécanique est la science qui étudie les mouvements et/ou les déformations, produits par des forces.
Pour traiter le problème du mouvement (la Mécanique), on se limite ici aux mouvements à vitesse constante (la valeur de la vitesse ne change pas, et la direction du mouvement reste la même). Ces mouvements sont appellés mouvements uniformes, ou translations uniformes.
On nomme observateurs galiléens deux observateurs qui sont en translation uniforme l’un par rapport à l’autre.
La conclusion vue plus haut a été généralisée grâce à de multiples expériences mécaniques faites par des observateurs galiléens :
Dans les exemples ci-dessus, le hunier est un premier observateur lorsqu’il lâche la pierre, navire à quai.
Il est un second observateur lorsqu’il la lâche, bateau en mouvement uniforme.
Dans les deux cas, il constate que la trajectoire de la pierre suit le mât.
L’impossibilité de distinguer les résultats des expériences de mécanique faites par deux observateurs galiléens se nomme équivalence des observateurs galiléens.
Puisque l’observateur doit évaluer des mouvements, il doit d’abord repérer la position d’un objet. Considérons un phénomène simple, comme le mouvement d’un boule de billard lancée sur une surface plane et horizontale. Pour pouvoir établir une loi du mouvement, il faut être capable de dire où se trouve la boule, à chaque instant. Il faut donc repérer la position, et le temps. Pour la position, il suffit de placer un mètre en ruban près de la trajectoire de la boule. Pour le temps, il faut une horloge. Donc, une ligne droite graduée (on l’appellera axe), et une horloge.
Plus généralement, si le mobile suit une courbe plus complexe, il faudra trois axes au lieu d’un (les trois étant bien sûr gradués). L’ensemble des trois axes constitue un repère, ou plutôt un référentiel. Les axes sont en général pris perpendiculaires les uns aux autres.
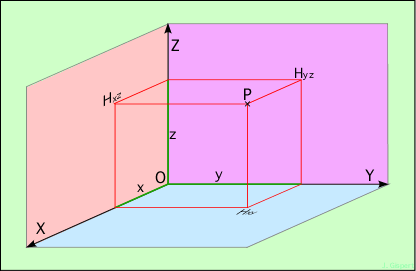
Un référentiel
Le point P est repéré par ses trois coordonnées x, y et z (en vert sur les axes). Pour les trouver, on construit le parallélépipède rectangle ayant pour sommets opposés le point P et l’origine O, et les arêtes parallèles aux axes. Les coordonnées sont les distances de P aux trois plans fondamentaux OXY, OXZ et OYZ.
Les trois axes jouent exactement le même rôle. Aussi, dans la suite, pour des raisons de simplicité, nous ne considérerons en général qu’un seul axe, l’axe X. Les formules qui s’en déduisent sont des modèles : il faut les reproduire pour Y et Z en changeant les noms des variables (changer x en y pour l’une, x en z pour l’autre).
A chaque observateur sera attaché un référentiel, dans lequel il est immobile (pour un expérimentateur, ce sera le laboratoire dans lequel il travaille).
On appelle repères galiléens, ou référentiels galiléens, ou repères inertiels, ou référentiels inertiels, des référentiels qui sont en translation uniforme l’un par rapport à l’autre.
Une conséquence immédiate est que deux observateurs galiléens, placés dans des cabines sans fenêtres, et faisant des expériences de mécanique, ne pourront jamais savoir s’ils sont en mouvement rectiligne uniforme ou au repos. Et cela implique que le repos n’existe pas ! On peut se croire au repos, et être en translation uniforme, même à une vitesse qui nous paraîtrait grande, sans s’en apercevoir. La preuve ? La Terre est en train de tourner sous vos pieds, et vous vous déplacez à la vitesse de 1.221 km h-1 (à la latitude de Marseille ; à l’équateur, c’est 1.670 km h-1, et aux pôles, c’est évidemment nul) sans le ressentir ! (Il s’agit de la vitesse circulaire autour de la Terre, mais sur un bref moment, on peut la considérer comme une vitesse linéaire). De même, dans un avion, à 800 km h-1, on ne ressent rien ; on peut verser une boisson dans un verre sans la renverser : le liquide, comme la pierre dans le bateau, est entraîné avec l’avion, et tombe bien dans le verre ! Par contre, on ressent très bien lorsque l’avion commence sa descente, car il y a un changement de vitesse (la vitesse n’est plus uniforme, mais à ce moment-là, l’hôtesse vous a retiré vos verres !) : les changements de vitesse concernent la Relativité Générale.
Remarquez de plus que, le repos absolu n’existant pas, la vitesse absolue n’existe pas davantage : on ne peut définir la vitesse d’un observateur que par rapport à un autre. Et cette notion est totalement symétrique : il est équivalent de dire que O1 se déplace à la vitesse v par rapport à O2, ou que O2 se déplace à la vitesse -v par rapport à O1 (le signe - parce que la direction est opposée : si O2 va vers l’ouest par rapport à O1, alors O1 va vers l’est par rapport à O2). Cette première notion de symétrie sera très importante pour fonder la Relativité Restreinte.
La Relativité Galiléenne indique que le mouvement est relatif
Elle ne s’applique qu’aux observateurs galiléens
Elle postule que la Mécanique est la même pour tous les observateurs galiléens
Nous n’avons pas l’habitude de raisonner ainsi, parce que nous disposons en permanence d’un référentiel qui nous semble absolu, la Terre. Et par rapport à lui, l’un des observateurs est souvent au repos. Mais songez qu’en fait, nous sommes entraînés par la Terre autour du Soleil (30 km s-1), par le Soleil dans la Galaxie (230 km s-1), qui se précipite vers Andromède (400 km s-1), etc. Quand on arrive au super-amas, le reste de l’Univers est fait d’objets de même nature, les autres super-amas. Lequel prendre comme repère absolu ?
Il n’existe donc pas de référentiel absolu auquel rapporter toutes les expériences, et donc nous ne pourrons jamais que rapporter l’une à l’autre. C’est cela la Relativité Galiléenne.
Incidemment, le repos et le mouvement uniforme sont équivalents ! Puisque chacun ne peut être défini que par rapport à un référentiel, il suffit que l’on prenne le référentiel de repos du corps, et un référentiel en mouvement uniforme par rapport à lui, et que l’on applique l’équivalence de ces deux référentiels.
Le principe d’inertie avait été envisagé avant Galilée, mais c’est lui qui l’a formalisé. Il résulte de ses travaux sur les plans inclinés. Il s’énonce :
Tant que le corps ne subit pas de force, il persévère donc dans ce mouvement.
Il est impossible de se placer dans les conditions exactes de ce principe : l’expérience de Galilée ne pouvait annuler les frottements de ses mobiles sur le plan incliné. Le principe est donc une extrapolation d’expériences réelles approchées.
Puisque la masse de l’objet d’expérience ne varie pas, ainsi que sa vitesse, leur produit ne change pas au cours du temps. Ce produit est nommé quantité de mouvement, ou impulsion, ce dernier terme étant préférable maintenant.
Il en résulte le principe de la conservation de la quantité de mouvement.
Si un système est constitué de deux corps, la quantité de mouvement totale du système est la somme des quantités de mouvements des deux corps. C’est elle qui se conserve. S’il y a interaction entre les deux corps, leurs vitesses peuvent changer, mais de telle manière que la quantité de mouvement totale du système reste inchangé. De là découle le principe de l’action et de la réaction. La conservation de la quantité de mouvement est l’un des grands principes de la physique.
Considérons deux observateurs galiléens. Supposons que l’un des deux étudie le mouvement d’un corps. Que voit l’autre s’il observe la même expérience ? Pour lui, le corps est en mouvement par rapport à l’autre observateur, qui est lui-même en translation uniforme par rapport à lui.
Ce problème fondamental est celui de la composition des mouvements. On considère trois observateurs galiléens en mouvement les uns par rapport aux autres :
O2 se déplace à la vitesse constante v1 par rapport à O1
O3 se déplace à la vitesse constante v2 par rapport à O2
A quelle vitesse se déplace O3 par rapport à O1 ?
L’illustration classique que nous verrons plus loin est la suivante :
O1 est le quai d’une gare ;
O2 est un train qui roule à v1 = 100 km h-1 par rapport à O1 (le quai) ;
O3 est un voyageur qui marche dans le train (O2) à v2 = 5 km h-1.
A quelle vitesse voit-on se déplacer le voyageur (O3) depuis le quai (O1) ?
Le problème qui se pose maintenant est de concilier deux physiciens qui auraient étudié le même phénomène dans deux référentiels différents. Les lois qu’ils ont trouvées sont-elles compatibles ? Ont-elle la même forme ? Et surtout, connaissant une loi déterminée dans le référentiel R, peut-on déduire la loi correspondante dans un référentiel différent R′, où personne n’a fait d’expériences ? (par exemple faire atterrir et redécoller un engin spatial sur une planète jusque-là inexplorée).
Puisque le cadre choisi concerne les référentiels galiléens, il faut déterminer comment passer d’un référentiel galiléen à un autre (par conséquent se déplaçant à vitesse constante par rapport au premier). La transformation de Galilée permet de calculer les coordonnées dans un référentiel O1, d’un point du référentiel O2, en translation uniforme par rapport à O1 :
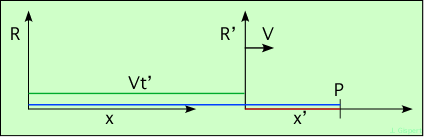
On voit sur le schéma deux référentiels (deux axes sont représentés), celui de droite R′ étant animé de la vitesse V par rapport à celui de gauche R (la vitesse est figurée par la petite flèche attachée à l’axe vertical). Le point P est repéré par son abscisse x&prime: dans R′. Mais on peut le repérer aussi par son abscisse x dans R. Connaissant x′, que vaut x ?
Formellement, il faut distinguer le temps dans les deux référentiels : t dans R, et t′ dans R′ (une horloge est attachée à chacun). Mais toutes les horloges mécaniques construites n’ont jamais montré la moindre différence de marche. Donc, rien ne permet, dans le domaine d’expérience considéré, de distinguer les deux temps : t = t′.
La réponse se voit sur le schéma : l’abscisse x de P dans R est représentée par le segment en bleu. Il s’obtient comme somme du segment vert et du segment rouge ; le premier est la distance V t′ parcourue par le référentiel R′ depuis l’origine du temps (où les origines coïncidaient) ; le second est l’abscisse x′ de P dans R′. Donc, x = x′ + V t′.
C’est la transformation de Galilée. Puisque nous avons choisi les axes de telle manière que Ox soit orienté comme la vitesse V, les deux autres coordonnées ne changent pas :
Transformation de Galilée
x = x′ + Vt′
y = y′
z = z′
t = t′
La première de ces relations explique que les coordonnées dans R se déduisent de celles dans R′ en ajoutant simplement la distance parcoure par R′ dans le temps t′. La dernière nous est naturelle, puisqu’elle dit que le temps est le même partout ! C’est le temps absolu de Newton.
La symétrie évoquée plus haut entre les deux observateurs se traduit par la possibilité de passer du référentiel R au référentiel R′, tout aussi bien que de R′ à R. En effet, la seconde des deux relations étant elle-même symétrique, se conserve : t′ = t. Partant de la première, on peut en tirer x′ = x - v t′. Mais puisque t′ = t, elle donne : x′ = x - v t, ou encore x′ = x + (-v) t. On retrouve exactement la même formule, avec la vitesse -v à la place de v. Mais c’est justement la vitesse du référentiel R vu de R′. Les formules de changement de référentiel sont donc inversibles.
La transformation de Galilée a été utilisée pour tous les besoins de la Physique jusqu’à ce qu’on la remette en cause à la fin du XIXe siècle.
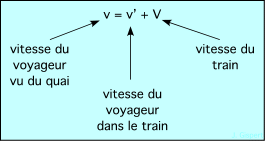
Cette transformation étant posée, la règle d’addition des vitesses en découle. Considérons un référentiel R, supposé au repos, et un référentiel R′ en translation uniforme par rapport à R à la vitesse V.
Dans le référentiel R′, un mobile se déplace à la vitesse v′. Quelle est la vitesse de ce mobile dans R ?
En utlisant la transformation de Galilée, il est aisé de montrer que :
C’est la règle d’addition galiléenne des vitesses. On la pratique intuitivement, parce qu’elle correspond à notre expérience quotidienne, conditionnée par des vitesses très faibles.
Dans le cas du train, on a :
En relativité galiléenne, les lois de la Mécanique sont les mêmes dans tous les référentiels galiléens (c’est-à-dire en translation uniforme). Ceci découle de l’équivalence des référentiels galiléens.
Question essentielle Si les deux observateurs en mouvement relatif uniforme obtiennent les mêmes résultats physiques, les traduiront-ils par les mêmes équations ? Autrement dit, la forme mathématique des phénomènes est-elle indépendante de l’observateur (galiléen) ? En répondant à cette question, on posera des barrières permettant de délimiter le terrain pour la Relativité Restreinte. Si les équations ont la même forme, on dit qu’elles sont invariantes par changement de référentiel.
Les expériences précédentes sont limitées, car les vitesses relatives sont très faibles. Elles définissent la Physique Classique, celle des petites vitesses qui nous est familière. Mais la technologie humaine est maintenant capable de produire des vitesses très grandes, qui sortent du domaine dans lequel la Physique Classique a été élaborée. On voit là une propriété fondamentale des lois de la Physique : elles sont établies dans un cadre bien défini, et sont donc valables dans ce cadre. En dehors, il est possible que les lois restent valables, mais il est possible tout autant qu’elles diffèrent. C’est bien ainsi qu’il faut concevoir la théorie de la Relativité Restreinte. Elle part du constat que la Physique Classique (Relativité Galiléenne) ne permet pas de sortir de son cadre des petites vitesses, ce que nous allons voir dans le chapitre suivant.
La pertinence de la Relativité Galiléenne dépend de la finesse des expériences correspondantes. Pour le problème du train, elle donne une réponse parfaitement satisfaisante (en accord avec l’expérience). Mais nous verrons que, si on remplace le voyageur par un rayon lumineux, la Relativité Galiléenne ne donnera pas la bonne réponse, car elle sort du cadre d’expériences qui la valident (les petites vitesses). C’est la Relativité Restreinte qui apportera la bonne explication.
Tout ce que nous avons dit jusque-là sur les référentiels et les observateurs, s’applique aussi à la Relativité Restreinte, la différence entre elles étant le rapport des vitesses considérées avec la vitesse de la lumière : si ce rapport est petit (vitesses des mobiles très petites devant la vitesse de la lumière, domaine de notre expérience quotidienne), alors la Relativité Galiléenne est pertinente, sinon (vitesses proches de c) c’est la Relativité Restreinte qui donne la réponse correcte.
Nous n’avons rien dit jusqu’ici à propos du temps. Il est admis que celui-ci est au-dessus de nos préoccupations, c’est une donnée aussi intangible que l’espace lui-même. Si le mouvement est relatif, le temps et l’espace sont, eux, absolus. Ils caractérisent la Physique Classique, le cadre Newtonien (dans laquelle il s’est développé). Le temps est une variable, dont la valeur est identique pour tous les observateurs !
En Physique Classique, le vide est l’absence de matière. Mais alors, qu’est-ce qu’un espace vide ? Pour le concevoir, il faudrait l’observer. Donc y être, et alors, il n’est plus vide… Admettons cependant que notre présence ne change rien. Qu’observerons-nous, s’il n’y a rien ? L’espace en lui-même n’est pas observable. Postuler qu’il existe est une vue de l’esprit !
Pour le temps, le problème est un peu le même. Comment mesurer le temps, s’il n’y a rien ? Pas le moindre repère, rien qui bouge… Là encore, l’existence du temps en-dehors de toute matière est une illusion !
Mais ces deux illusions ont été enracinées dans notre compréhension du monde, par des phénomènes de prolongement. Ce qui existe ici et maintenant doit exister aussi ailleurs, et dans un autre temps. Et cette illusion est la base de toute la physique pré-relativiste (Relativité Galiléenne).
La dynamique est l’étude du mouvement des corps. Partant du principe d’inertie, un corps qui ne subit pas de forces continue sur sa lancée. Mais si une force lui est appliquée, son mouvement en est affecté.
L’accélération d’un mobile est la variation de sa vitesse. Il est évident qu’elle concerne les changements dans la grandeur de la vitesse : pour passer de 50 km h-1 à 100 km h-1 en ligne droite, une voiture subit une accélération. Mais à vitesse linéaire constante, il faut aussi une accélération pour changer de direction. On le ressent bien lorsque, passager d’une voiture, on prend un virage serré. De la même manière, la Lune dont la vitesse a toujours à peu près la même grandeur, subit en permanence de la Terre une accélération (de la pesanteur, ou gravitationnelle), qui courbe sa trajectoire.
Le principe fondamental de la dynamique est la proportionnalité entre l’accélération et la force :
f = m γ
Vous pouvez trouver ici la méthode géométrique utilisée par Newton pour l’obtenir.
Toute la Mécanique Céleste (en particulier) est basée sur cette identité. Elle relie deux notions de nature différente : la force est une notion dynamique (grec dynamis : puissance), alors que l’accélération est une notion cinématique (grec kinema : mouvement). Elle indique donc qu’une force produit un mouvement.
Elle s’écrit aussi : f = dp / dt, où p = m v.
dp / dt est la dérivée, par rapport au temps, de la vitesse, c’est-à-dire le changement de vitesse ; p est nommé impulsion. C’est sous cette forme qu’elle sera reprise par la Relativité Restreinte.
Jusqu’ici, nous avons parlé de la Mécanique et de l’invariance de ses lois par transformation de Galilée. Mais qu’en est-il de l’électromagnétisme ?
Si on applique la transformation de Galilée aux quatre équations de Maxwell, qui définissent l’électromagnétisme, on s’aperçoit qu’elles ne sont pas toutes invariantes. Par conséquent, l’électromagnétisme, théorie qui a pourtant fait ses preuves, n’est pas compatible avec la Relativité Galiléenne. Ceci sera expliqué plus en détails dans le chapitre suivant…
La Relativité Galiléenne est une étude des points de vue différents de deux observateurs, en translation uniforme l’un par rapport à l’autre, sur un même phénomène.
Tous les observateurs partagent le même espace et le même temps.
Principe d’inertie : les expériences de Galilée lui ont permi de définir le principe d’inertie
un corps en mouvement, s’il ne subit aucune force extérieure, continue ce mouvement dans la même direction, à vitesse constante.
Principe de Relativité Galiléenne : les lois de la Mécanique sont invariantes dans la transformation de Galilée.
Observateurs galiléens : les observateurs galiléens sont en translation uniforme l’un par rapport à l’autre (si la vitesse de deux observateurs n’est pas constante, ils ne sont pas galiléens).
Equivalence des observateurs galiléens : deux observateurs galiléens, qui font les mêmes expériences de Mécanique, obtiennent les mêmes résultats.
Le repos absolu n’existe pas : il est impossible à un observateur galiléen de savoir, en faisant des expériences de mécanique, s’il est en mouvement ou au repos.
Il n’existe pas de référentiel absolu : c’est une conséquence de l’absence de repos absolu.
Le temps est absolu : il est le même pour tous les observateurs galiléens. La transformation de Galilée ne fait donc intervenir que les positions dans les deux référentiels (et leur vitesse relative).
Addition des vitesses : conséquence de la transformation de Galilée.
Relation fondamentale de la dynamique : f = m γ.
Cadre de l’expérience quotidienne : la transformation de Galilée ne s’applique que pour les vitesses faibles devant celle de la lumière, et pour des observateurs galilélens. Elle est à la base de toute la Physique Classique non relativiste.
Les principes qui supportent cette théorie sont validés indirectement par les expériences, par l’intermédiaire des lois qu’ils permettent d’établir, et dans le cadre cité.
---=OO=---