Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Diagramme HR | |||||||
Dans toutes les sciences en création, la classification joue un rôle essentiel. Avant de comprendre les phénomènes en action, il faut reconnaître les similarités et les différences entre les objets étudiés. Prenons deux exemples :
Ainsi, le comportement collectif des objets d’étude peut mettre en lumière une propriété cachée, dans notre exemple le magnétisme. Si on refaisait l’expérience avec un mélange d’aiguilles en bois et en fer, on constaterait que les aiguilles de bois se répartissent au hasard, alors que les aiguilles de fer s’orientent. Ceci définit deux populations de comportement différent. Par contre, dans chaque population, le comportement est le même. Cette observation n’explique pas pourquoi les aiguilles se comportent ainsi. Mais elle montre qu’il y a un phénomène à rechercher.
Les sciences de la Vie ont d’abord étudié minutieusement les particularités des êtres vivants, pour les regrouper selon la taxonomie. Plus tard, la génétique a permi de comprendre l’origine des différences et des similitudes.
L’astrophysique n’a pas échappé à cette méthode. Créé par Ejnar Herzsprung et Henry Russell, le diagramme HR (ou diagramme Hertzsprung-Russel) est l’outil essentiel de l’astrophysique pour la classification des étoiles et leur évolution. Il place ces dernières sur un graphique à deux dimensions : le type spectral et la luminosité. Si ces deux propriétés n’avaient pas de lien entre elles, les points représentatifs des étoiles dans le diagramme seraient répartis au hasard. Une concentration, au contraire, met en lumière un lien. C’est ce qu’il s’est produit lorsque ces deux astronomes ont, chacun de son côté, opéré ce classement. Prenons par exemple les étoiles de type solaire (type spectral G2) ; sur un large échantillon, on s’aperçoit qu’une grande proportion d’entre elles présentent à peu de choses près la même luminosité. Il en est de même pour les autres types spectraux : à type spectral donné, luminosité correspondante.
 Un pseudo-diagramme avec des points non corrélés |
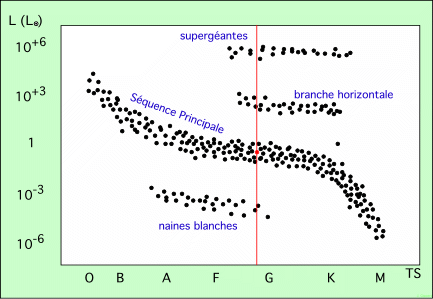 Un diagramme réel simplifié |
Le schéma de gauche montre ce que serait le diagramme HR si la luminosité des étoiles était indépendante de leur température. Les points seraient répartis au hasard, on n’y voit aucune information. Par contre, le schéma de droite est proche d’un schéma réel, et montre des concentrations des points représentatifs des étoiles. On y voit en premier la ligne en S couché, qui représente la Séquence Principale. 80 % des étoiles observées se trouvent là, parce que les étoiles y passent la plus grande partie de leur vie.
Au-dessus de la Séquence Principale, on voit une ligne horizontale formée par des étoiles plus brillantes que le Soleil. Elles forment la Branche Horizontale. Plus haut encore, on voit la zone des supergéantes (explication plus loin). Enfin, en-dessous de la Séquence Principale, on voit la zone des Naines Blanches. Ce nom est doublement mal choisi, car ces étoiles ne sont pas des naines (les naines sont les étoiles de la Séquence Principale). Elles sont bien plus petites. Et blanches, elles ne le sont pas non plus ; elles le sont juste à leur formation, lorsqu’elles sont encore très chaudes. Mais en se refroidissant (puisqu’elles n’ont plus de source d’énergie pour maintenir leur température), elles deviennent jaunes, puis rouges, jusqu’à disparaître au regard. Mais ce refroidissement est très lent.
La répartition particulière des étoiles dans ce diagramme montre qu’il est pertinent, qu’il y a des liens physiques entre ses deux paramètres, type spectral (qui caractérise la physique de l’étoile) et luminosité (qui indique la puissance de l’étoile). La connaissance, la mesure, de l’un donne une idée de la valeur de l’autre. Si toutes les étoiles d’un même type spectral se regroupaient, ce lien serait une équivalence. Ce n’est pas le cas, ce qui montre qu’un autre paramètre joue également un rôle, nous le verrons plus loin.
La ligne rouge verticale qui traverse le diagramme figure le type spectral du Soleil (G2). Elle coupe la Séquence Principale, mais aussi la Branche Horizontale et la branche des supergéantes. Elle sera expliquée plus loin. Le point rouge représente le Soleil.
A l’origine, le diagramme créé par les deux astronomes était un diagramme couleur-magnitude. Mais la couleur est une notion quelque peu subjective. Pour lui donner une consistance, on photographie l’étoile en noir et blanc à travers deux filtres différents, B (bleu ; centré sur 442 nm, déborde sur l’UV) et V (visible ; centré sur 540 nm, au centre du domaine visible). La différence d’éclat entre les deux photos, nommée indice B-V, indique si l’étoile est plus ou moins bleue. C’est une véritable mesure physique. Précisément, B est la magnitude de l’étoile photographiée à travers le filtre B (idem pour V).
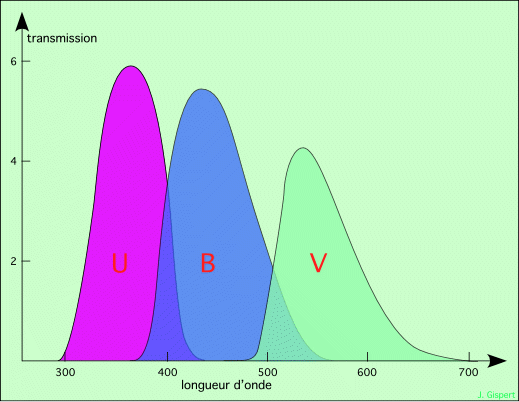
Transmission des filtres U, B et V (longueurs d’onde en nanomètres)
Au lieu de photographier une étoile unique, on photographie un amas entier sur les mêmes pellicules (en B et V). On a donc deux clichés en moir et blanc, mais quand on les compare, on voit que certaines étoiles sont plus brillantes sur l’un que sur l’autre.
Prenons par exemple une étoile plus brillante sur le cliché B que sur le cliché V. Sa lumière contient davantage de violet et de bleu, que de vert et de jaune. Son maximum d’éclat se trouve par conséquent du côté bleu, et c’est de cette couleur qu’elle nous apparaît dans un télescope. On peut mesurer sa brillance sur le cliché B. Ce que l’on mesure ainsi est la quantité de lumière qui a traversé le filtre B, c’est donc la luminosité LB de l’étoile, modulée par la distance à laquelle elle se trouve.
L’indice de couleur B-V est par définition la différence des magnitudes : B-V = mB - mV. Or la magnitude est d’autant plus grande que la luminosité est plus faible (une étoile de magnitude 6 est à la limite de la visibilité, alors qu’une autre de magnitude 1 est bien brillante). Donc, plus il y a de lumière, plus la magnitude est petite. C’est-à-dire que :
| luminosités | dominante | magnitudes | B-V |
|---|---|---|---|
| LV < LB | bleu domine | mB < mV | B-V < 0 |
| LV = LB | pas de dominante | mB = mV | B-V = 0 |
| LV > LB | vert domine | mB > mV | B-V > 0 |
B-V = mB - mV est : négatif s’il y a plus de bleu que de vert, nul s’il y en a autant, et positif s’il y en a moins.
La magnitude s’obtient à partir de la luminosité par la loi de Pogson : m = -2,5 log L + cste. On obtient donc la magnitude en B par mB = -2,5 log LB + cste, où LB est le résultat de la mesure. On procède de même en V, pour obtenir mV. L’indice de couleur B-V est la différence entre ces deux magnitudes : B-V = mB - mV = (-2,5 log LB + cste) - (-2,5 log LV + cste) = 2,5 log (LV / LB) |
Prenons maintenant une étoile qui nous paraît plus brillante sur l’autre cliché, en V. A l’œil, elle nous apparaît plutôt jaune. Puisqu’elle est plus brillante en V, sa magnitude en V est plus petite qu’en bleu : mV < mB ; donc B-V est positif.
Une étoile qui nous paraît plus brillante sur le cliché pris avec le filtre V est telle que LB < LV, donc mB > mV et mB - mV = B-V > 0.Une étoile qui, au contraire, est plus brillante en bleu est telle que LB > LV, donc mB < mV et mB - mV = B-V < 0.
L’indice de couleur B-V nous renseigne sur la couleur de l’étoile, mais nous renseigne de façon chiffrée, c’est-à-dire comparable entre deux étoiles. Alors que, dire qu’une étoile est plus bleue que l’autre, ne nous apprend pas grand chose…
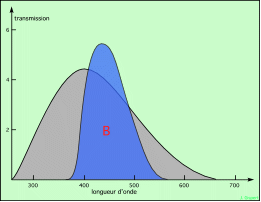 étoile chaude, filtre B |
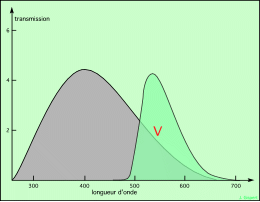 étoile chaude, filtre V |
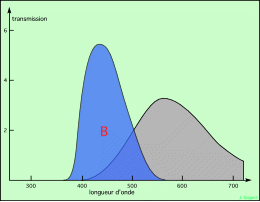 étoile froide, filtre B |
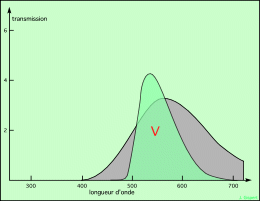 étoile froide, filtre V |
Les quatre schémas ci-dessus montrent un spectre de corps noir, en gris, correspondant à une étoile chaude en haut (maximum vers 400 nm, température de 7.200 K, type spectral F1), et à une étoile plus froide en bas (maximum vers 570 nm, température de 5.000 K, type spectral G9). Le premier schéma montre la partie de lumière qui passe le filtre B : c’est celle qui correspond à la surface en bleu soutenu. Plus cette surface est grande, plus importante est la lumière reçue de l’étoile dans ce domaine ; et plus petite est la magnitude correspondante. De même, le schéma de droite en haut montre la partie de lumière qui passe le filtre V. Elle définit la magnitude V. La surface en bleu soutenu est plus grande que celle en vert soutenu, donc B < V, donc B-V < 0.
Les deux schémas du bas montrent la même chose, mais pour une étoile plus froide. Du fait du décalage du spectre vers les grandes longueurs d’onde, les choses sont inversées : B > V, donc B-V < 0.
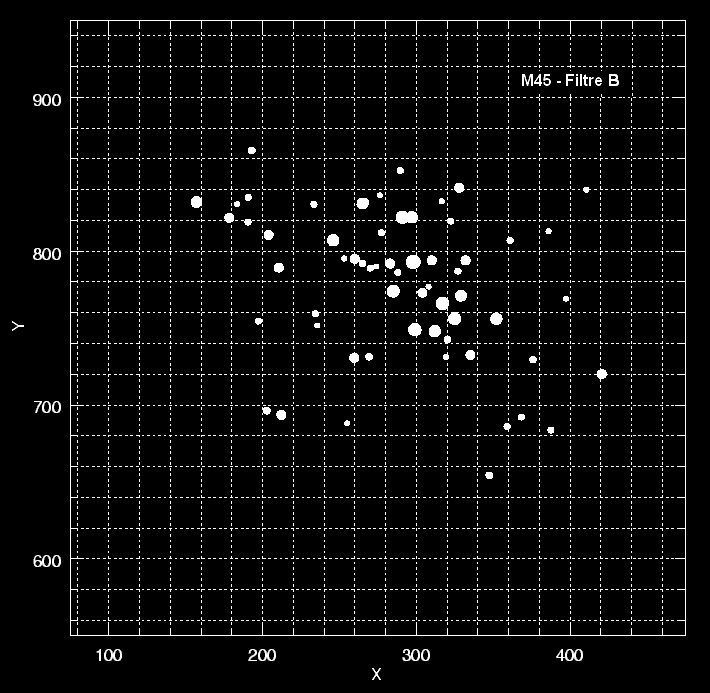 image filtrée B |
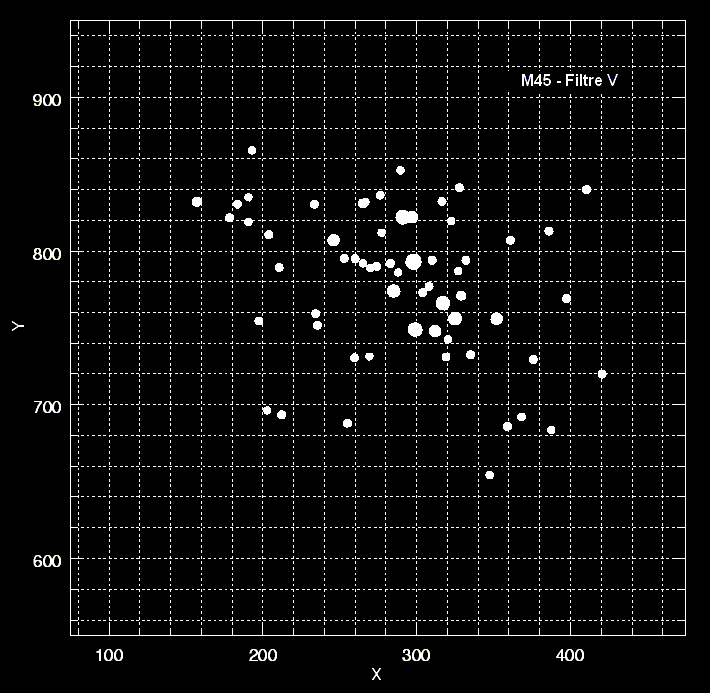 image filtrée V |
Pour le visualiser, il suffit d’afficher alternativement les deux images en un film continu :
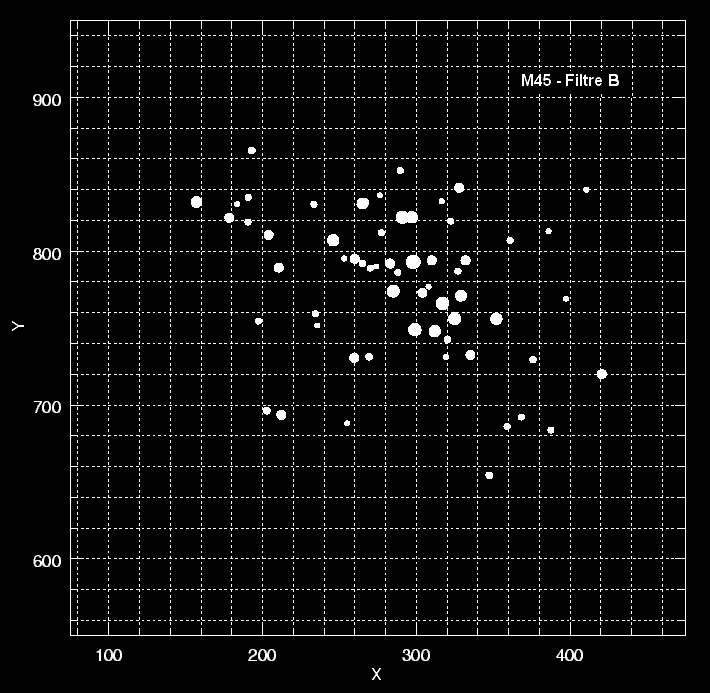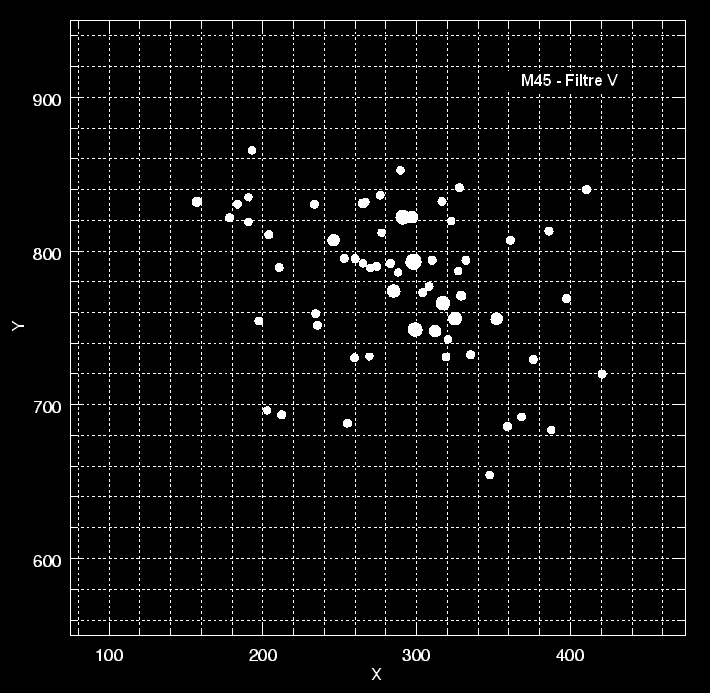
Il ne reste plus qu’à faire ces mesures patiemment pour toutes les étoiles du cliché… et à les reporter sur un graphique.
Maintenant que nous sommes passés à la photo numérique, les clichés peuvent très bien être de fichiers électroniques. Et ces fichiers peuvent être analysés automatiquement par un logiciel relativement facile à écrire… qui donne les valeurs de B (ou de V) directement pour chaque étoile. Il ne reste plus alors qu’à compléter le programme pour qu’il analyse successivement les deux clichés, et calcule les différences. Pour construire le diagramme HR de l’amas, il reste une difficulté : les mesures que nous venons de faire dépendent de la distance de l’amas. Il est possible de calibrer le logiciel, en lui faisant analyser un amas dont les magnitudes sont connues, pour ajuster les valeurs qu’il donne. Mais les magnitudes calculées seront toujours des magnitudes apparentes ! Et la distance des étoiles est bien difficile à mesurer…
Toutefois, nous avons choisi de photographier un amas. C’est bien naturel, puisqu’on a une foule d’étoiles sur le même cliché. Mais il y a un avantage de plus : toutes ces étoiles se sont formées en même temps, au même endroit. Evidemment, elles sont à une certaine distance l’une de l’autre, distance que nous ne connaissons pas. Mais de toutes façons, cette distance est petite par rapport à la distance d’ensemble de l’amas. On peut donc considérer, en faisant une erreur minime, que toutes les étoiles sont à la même distance de nous, et que leur lumière est affaiblie pareillement. Donc, leur magnitude absolue diffère de leur magnitude apparente d’une même constante, qui ne dépend que de la distance de l’amas. Ne cherchons pas à déterminer celle-ci, il nous suffira d’avoir un axe vertical gradué en magnitudes apparentes… Gardons ce problème pour plus tard !
La lumière qui a impressioné la pellicule est celle qui a traversé le filtre. Elle est donc proportionnelle à la surface du spectre dont nous avons parlé plus haut, et donc à la luminosité de l’étoile. Ce qui a été dit plus haut s’applique donc pareillement à l’image de l’étoile sur la pellicule. Pour mesurer la magnitude apparente, il suffit de mesurer le diamètre de l’image de l’étoile. En effet, plus il y a de lumière, plus celle-ci diffuse dans la pellicule, ou dans le capteur numérique. A une étoile plus brillante correspond une tache plus grosse. Notre logiciel est tout à fait capable de mesurer les diamètres, donc d’obtenir les magnitudes apparentes de toutes les étoiles.
Nous avons maintenant les magnitudes et les couleurs. Il ne reste qu’à reporter ces valeurs dans un graphique, ce que le logiciel peut faire encore très facilement.
Les pionniers l’ont fait, pour leur part, à la main…
Le diagramme ci-dessous a été fait à l’aide d’un tel logiciel. Comment le trouvez-vous ?
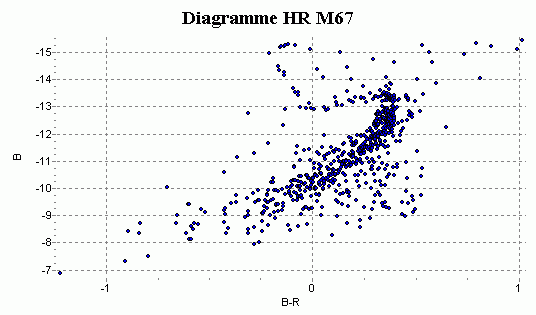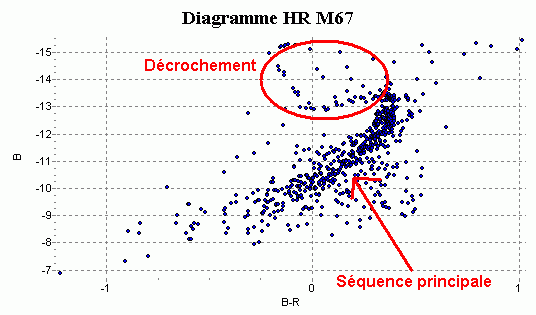
diagramme généré automatiquement Marc Deldem, sur un forum
Vous avez sans doute remarqué que la pente de la séquence principale est inversée par rapport à celle d’un diagramme HR. Pour comprendre cela, il faut considérer la graduation de l’axe des abscisses x : elle indique B-R, R correspondant au filtre Rouge, et les valeurs vont de -1 à gauche à +1 à droite. Si par exemple B-R = +1, ceci signifie que B = R + 1 ; B est donc plus grand que R. Cette étoile rayonne davantage dans le bleu-violet que dans le rouge, c’est donc une étoile chaude. Or dans le diagramme HR, les étoiles chaudes sont à gauche et non à droite ! Ceci explique l’inversion.
Le diagramme HR se décline en diverses formes, selon le choix que l’on fait pour les deux paramètres. Le type spectral et la luminosité étant les choix de base, on peut les remplacer par d’autres, qui sont équivalents, liés par la physique des étoiles.
Considérons tout d’abord l’axe horizontal :
La théorie du fonctionnement des étoiles montre que leur masse est le paramètre essentiel qui définit toutes leurs propriétés (c’est le théorème de Vogt-Russell), mais il existe une dépendance secondaire selon la composition chimique de l’étoile. La masse peut donc être substituée aux autres données citées, si on néglige l’influence de la composition chimique. Ce n’est donc qu’une approximation qui n’a pas de véritable caractère scientifique, mais qui peut donner une idée générale.
Considérons maintenant l’axe vertical : la luminosité de l’étoile est la quantité de lumière qu’elle émet, l’énergie produite. Elle a un sens physique. Cette lumière se répartit sur une sphère de très grande surface à la distance de la Terre. Et nos télescopes en captent une petite partie, qui correspond à la surface du miroir. C’est cette petite quantité de lumière qui définit la magnitude apparente de l’étoile. Cette donnée est bien sûr inutilisable, puisqu’elle dépend de la distance. La magnitude apparente, corrigée pour ramener l’étoile à une distance standard de 10 parsecs, définit la magnitude absolue, qui est équivalente à la luminosité, puisque débarrassée de la distance. On peut donc l’utiliser en lieu et place de la luminosité.
Avec ces paramètres, on peut définir divers types de diagrammes HR. La figure ci-dessous les regroupe tous, pour illustrer le propos.
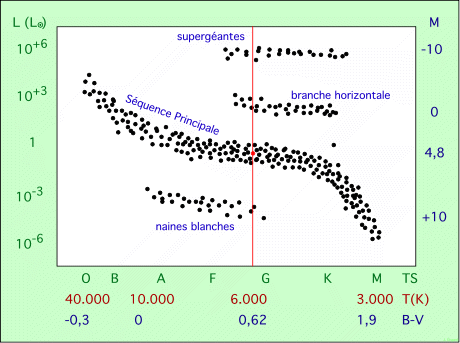
Diagramme montrant les 5 paramètres possibles
Les transformations pour passer d’un paramètre à un autre ne sont pas parfaitement définies, et la conversion introduit toujours de petites erreurs.
On remarque que la température effective croît de la droite vers la gauche, ce qui est assez inhabituel. La raison est que le type spectral a été utilisé historiquement avant, et que celui-ci est basé sur un ordre alphabétique initial, par la suite corrigé. C’est le reste de cet ordre, OBAFGKM, qui détermine le sens gauche-droite du diagramme. Quand on passe du type spectral à la température, pour ne pas symétriser le diagramme, on admet une croissance de droite à gauche.
Puisque plusieurs paramètres peuvent être utilisés sur chaque axe, y a-t-il un choix standard ? Ce serait bien pratique, puisque tous les diagrammes HR se ressembleraient. Mais ce n’est pas le cas. En effet, si on fait une étude théorique, on préférera utiliser le type spectral, qui est le paramètre permettant de classer les étoiles. Mais si on construit le diagramme à partir de données observationnelles, ce sont des paramètres directement issus de l’observation qui seront utilisés, ne nécessitant pas de transformation qui induirait inévitablement de petites erreurs. Dans ce cas, la magnitude absolue est le paramètre le plus direct, mais il nécessite cependant la détermination de la distance, qui n’est pas toujours disponible. Aussi, l’utilisation des filtres B et V est souvent préférée, et c’est l’indice de couleur qui sera préféré. A une soustraction près, il est directement le résultat d’une mesure.
Nous avons envisagé d’utiliser la masse d’une étoile comme paramètre en abscisse. Pourrions-nous, avec la même approximation, envisager le rayon de l’étoile ? Le premier examen du diagramme nous indique que non. Si c’était le cas, à une température donnée (une ligne verticale dans le diagramme) correspondrait une position (une luminosité) unique dans le diagramme. Or nous voyons que, pour la température du Soleil par exemple de 5.800 K, on trouve de nombreuses étoiles autour de la luminosité du Soleil, mais on en trouve aussi bien plus haut et bien plus bas dans le diagramme. Il ne s’agit pas, comme pour la masse, d’une approximation, mais d’un problème bien plus important : à une température donnée correspondent plusieurs luminosités différentes !
Les étoiles situées plus haut sont bien plus lumineuses, en ayant la même température superficielle. Or la température effective donne la luminosité par unité de surface (loi de Stefan-Boltzmann énergie E = σ T4). Pour avoir, à une température donnée, une luminosité plus grande, il faut présenter une surface émissive plus grande. Surface plus grande signifie rayon de l’étoile plus grand. Ces étoiles qui se placent en haut du diagramme ont donc une taille plus grande que leurs voisines placées plus bas. Symétriquement, les étoiles moins lumineuses qui se trouvent en-dessous sont plus petites.
Lorsqu’on a découvert ces étoiles plus grosses que la "normale", on les a assez naturellement nommées géantes. Et par opposition, on a nommées naines les étoiles normales.
Ceci est la base de la définition des classes de luminosité. On distingue :
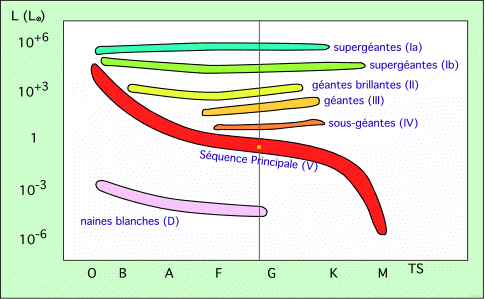
Les classes de luminosité
A ces classes définies d’abord, se sont ajoutées la classe D des naines blanches, les étoiles de rayon le plus petit. La classe Sd des sous-naines, copie moins lumineuse de la Séquence Principale (non représentée, elle se situe entre la Séquence Principale et les naines blanches). Enfin, la classe I des supergéantes a été subdivisée en Ia et Ib, la seconde correspondant à une luminosité plus faible, et une classe O a été ajoutée pour les hypergéantes (au-dessus des supergéantes).
Les étoiles considérées jusqu’ici sont des étoiles du voisinage solaire, c’est-à-dire formées dans la même région de la Galaxie, à une époque comparable. C’est la population II, de métallicité voisine de 2 %. Les étoiles qui se sont formées longtemps avant ont une métallicité très faible, et constituent la population I. Comme l’indique le théorème de Vogt-Russel, ces étoiles ont un fonctionnement un peu différent. La raison en est que, en l’abscence de carbone, le cycle du carbone ne peut se réaliser, et l’étoile ne tire son énergie que de la chaîne proton-proton. Il s’ensuit que ces étoiles sont un peu moins lumineuses que celles de la Séquence Principale, et donc se placent dans le diagramme HR en-dessous de cette dernière. C’est la classe des sous-naines.
Le fonctionnement d’une étoile consiste à trouver un équilibre entre la gravité qui tend à les écraser, et la pression développée par les réactions nucléaires internes. Toute variation de cet équilibre, par disparition progressive de l’hydrogène initial, se traduit par des changements de leur température superficielle et de leur luminosité. Et par conséquent, le point qui représente l’étoile dans le diagramme HR se déplace : vers le haut si la luminosité augmente, vers la gauche si c’est la température. Par conséquent, l’évolution de l’étoile, depuis sa formation jusqu’à sa fin, se traduit par une ligne courbe dans le diagramme. Et l’observation de cette ligne permet de comprendre le chemin évolutif suivi par l’étoile. Seul défaut, le diagramme HR ne représente pas le temps, et la vitesse est variable le long du chemin évolutif. Certains segments sont parcourus à grande vitesse (quelques centaines ou quelques milliers d’années), alors que d’autres sont parcourus à vitesse très faible (en quelques milliards d’années).
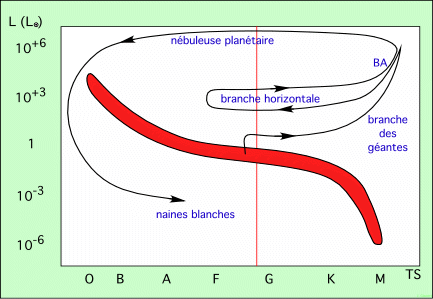
évolution d’une étoile de type solaire
Il n’est pas question de représenter toutes les évolutions possibles sur un diagramme. A titre d’exemple, nous prenons une étoile de 1,2 M, à la limite entre les parties basse et haute de la Séquence Principale (limite de la domination de la chaîne proton-proton au bénéfice du cycle de carbone) :
Les étoiles se forment de la contraction d’un nuage de gaz (H et He) et de poussières, qui est au départ à une température très basse de 10 K. La densité de ce nuage, forte par rapport au milieu environnant, est cependant très faible, et les chocs entre atomes très rares. La contraction commence donc sans échange d’énergie entre les atomes, c’est-à-dire en chute libre. La température du nuage n’augmente donc pas, c’est une contraction isotherme. Il ne brille pas non plus, si ce n’est un faible rayonnement de corps noir à 10 K. Plus tard, la densité commence à augmenter, et les chocs se font moins rares. Ce qui a pour effet d’augmenter la température. Mais le nuage reste transparent, et cette élévation très faible. La densité augmentant toujours, le gaz commence à s’opacifier. Dès lors, l’énergie s’échappe plus difficilement, et la température augmente. Le centre du nuage commence à briller. Par conséquent, le point représentatif du nuage dans le diagramme HR part d’une région où la température est très basse, donc très loin à droite (en dehors de tout diagramme dessiné !), et très bas puisque la luminosité est extrêmement faible. Dans la contraction, luminosité et température augmentent, et donc le point représentatif se déplace vers la gauche et vers le haut. L’opacité du gaz devient très importante, et le rayonnement ne passe plus. Si l’énergie restait vraiment piégée dans le gaz, sa température monterait très vite, et s’opposerait à la contraction. Mais cette chaleur crée une instabilité, et un mécanisme de convection se met en place. La totalité du gaz est ainsi brassée, et on a une protoétoile totalement convective. Lorsque c’est le cas, son point représentatif se trouve juste à droite de la Séquence Principale. Il est aisé de comprendre que l’énergie produite par cette protoétoile est d’autant plus importante que sa masse est plus forte. Mais l’efficacité du refroidissement par convection détermine une température qui est pratiquement indépendante de la masse. Et donc, les étoiles à ce stade sont représentées dans le digramme HR par une ligne presque verticale (température identique partout), et s’étalant en hauteur sur l’étendue des températures possibles.
Cette ligne n’est pas visible sur un diagramme HR réel. En effet, elle est théorique, et bien que les étoiles y passent lors de leur formation, elles n’y restent que très peu de temps, et à un instant donné il n’y en a donc qu’un tout petit nombre.
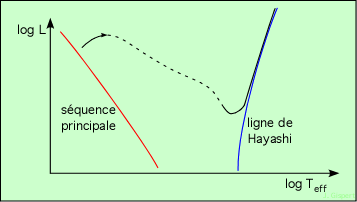
Le trajet de Hayashi
Les protoétoiles dans cette région continuent de se contracter, en brillant par leur énergie gravitationnelle. Mais le cœur se contracte plus vite que l’enveloppe, et sa température monte rapidement. Le point représentatif se déplace donc vers la gauche. La brillance de la protoétoile dépend de sa masse, et donc aussi la hauteur du point qui la représente. Rapidement, la protoétoile parvient à une temprature centrale qui permet le déclenchement des réactions de fusion de l’hydrogène. Elle devient alors une véritable étoile, et se trouve sur la Séquence Principale.
La ZAMS est la ligne inférieure de la Séquence Principale. Celle-ci présente une épaisseur : pour un type spectral donné, on voit plusieurs points sur la ligne verticale correspondante. Si les étoiles ne changeaient absolument pas sur la Séquence Principale, celle-ci serait une ligne fine. Mais cette phase dans la vie de l’étoile correspond à la fusion de l’hydrogène dans son cœur. Et l’hydrogène est comme le carburant d’une voiture : plus on en consomme, plus la voiture s’allège. De même, l’étoile subit quelques changements mineurs au cours de cette phase, qui se traduisent dans le diagramme HR par une ligne évolutive à l’intérieur même de la Séquence Principale.
La ligne inférieure de la Séquence Principale est celle sur laquelle les étoiles arrivent au moment où elles commencent la fusion de l’hydrogène. On a pour habitude de dater l’âge des étoiles à partir de cet instant. Par conséquent, les étoiles qui se trouvent sur cette ligne ont un âge nul, ce qui a donné le sigle ZAMS : Zero Age Main Sequence, ou Séquence Principale d’Age Zéro.
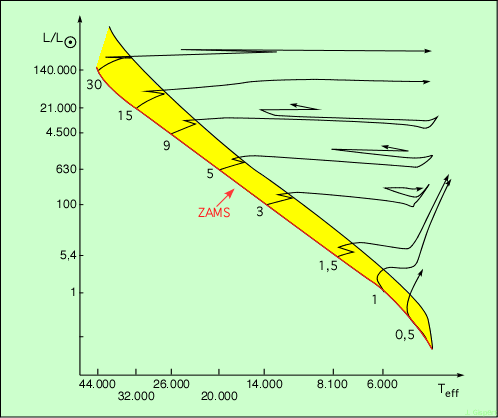
La ZAMS dans le diagramme HR
Ce schéma se trouve dans le chapitre consacré à l’évolution des étoiles.
Les flèches qui partent de la SP représentent le trajet évolutif des étoiles lorsque, l’hydrogène central étant épuisé, elles doivent trouver d’autres sources d’énergie pour maintenir leur équilibre. Mais ceci entraîne des modifications profondes, qui se font rapidement. Selon leur masse, indiquée par les nombres sous la ZAMS, ces étoiles auront des destins différents.
Quittant la Séquence Principale, l’étoile monte la branche des géantes (rouges), au sommet de laquelle elle subit éventuellement le flash de l’hélium. Redescendant alors, elle vient se stabiliser sur la Branche Horizontale. Elle parcours celle-ci de la droite vers la gauche, augmentant sa température effective, puis dans l’autre sens en se refroidissant. Ceci montre que l’équilibre sur cette branche (fusion de l’hélium) n’est pas très stable, en tous cas moins que sur la Séquence Principale.
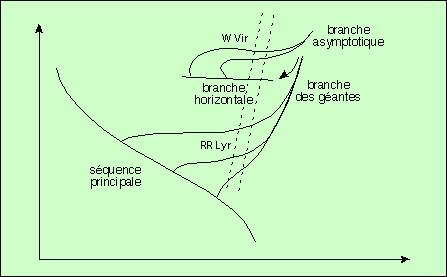
Passage de la branche horizontale à la branche asymptotique
Lorsque l’hélium s’épuise à son tour, l’étoile doit modifier son équilibre. Le cœur se contracte encore, la température centrale augmente. L’étoile s’approche, si elle le peut (masse suffisante) de la fusion du carbone. Elle monte encore dans le diagramme HR, son enveloppe se dilate encore un peu, elle va devenir une supergéante si elle est massive, sinon, elle éjectera son enveloppe sous forme de nébuleuse planétaire et redescendra le diagramme sur la gauche, en direction de la zone des naines blanches, sous la Séquence Principale.
Cette montée se fait sur la banche asymptotique. Celle-ci est ainsi nommée parce qu’elle part de la branche horizontale, et s’approche asymptotiquement du trajet de Hayashi. La raison en est que, lorsque l’étoile se transforme par contraction du cœur, l’énergie produite augmente, et sa dissipation devient de plus en plus difficile. Le transfert radiatif laisse progressivement le pas à un échange convectif. L’étoile devient peu à peu totalement convective, et donc s’approche du trajet de Hayashi. Mais elle ne peut le franchir, et donc s’en approche de plus en plus, et de moins en moins vite.
Après avoir monté cette branche, l’étoile la redescend pour aller se stabiliser sur la branche des supergéantes. Qu’elle quittera pour devenir une supernova…
Si la Séquence Principale est une phase très stable, les autres le sont moins. Et les étoiles qui traversent la branche horizontale subissent des soubressauts, à l’aller et au retour. On a montré qu’elles traversent en fait une zone de turbulences, qui est nommée bande d’instabilité.
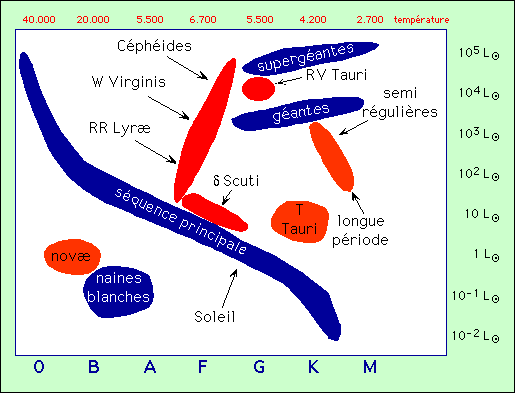
Passage de la branche horizontale à la branche asymptotique
La bande d’instabilité est la zone rouge diagonale qui contient les Céphéides, les W Virginis, et les RR Lyræ.
Il y a de multiples usages du diagramme, plus ou moins directs. Le plus évident est le suivi de l’évolution stellaire. Mais un usage plus subtil permet de déterminer l’âge d’un amas stellaire.
On considère que toutes les étoiles d’un amas se sont formées aux dépends d’un même nuage moléculaire, de son effondrement. Elles ont donc toutes le même âge. Il s’en est formé de toutes masses. Mais les étoiles de grande masse évoluent beaucoup plus vite que les étoiles de faible masse. Comme des coureurs qui auraient des vitesses très différentes. Partant au même moment, le plus rapide arrive le premier. L’étoile la plus massive quitte la Séquence Principale la première, et devient géante rouge. Les étoiles les plus massives se trouvant à gauche de la Séquence Principale, celle-ci s’en trouve raccourcie de ce côté-là. Plus le temps passe, plus elle s’use par la gauche… Alors, il devient très simple de déterminer l’âge d’un amas, simplement en regardant où sa Séquence Principale est coupée. Le point de coupure donne le type spectral des étoiles les plus massives qui n’ont pas encore quitté la Séquence Principale. Et comme la théorie nous dit combien de temps une étoile y passe, selon son type spectral, l’âge de l’amas s’en trouve défini.
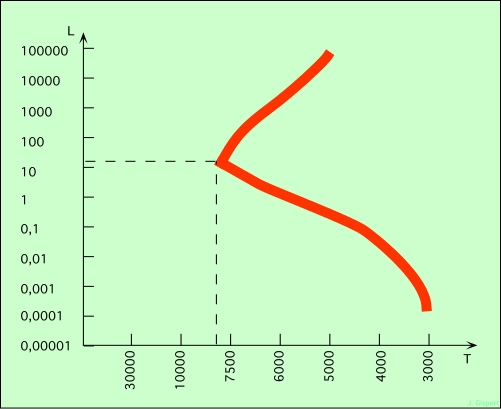
Le coude dans le diagramme HR d’un amas
Si on estime la luminosité des étoiles du coude sur le schéma, on mesure à peu près 15 fois la luminosité du Soleil. Comme la luminosité croît avec la puissance 3,5 de la masse, ceci nous donne une masse de 2,2 masses solaires. En reprenant la formule qui donne la durée de vie, on obtient V = 10 / M2,5 = 1,4 milliards d’années. C’est l’ordre de grandeur de l’âge de l’amas.
Ceci est détaillé dans le chapitre évolution des étoiles.
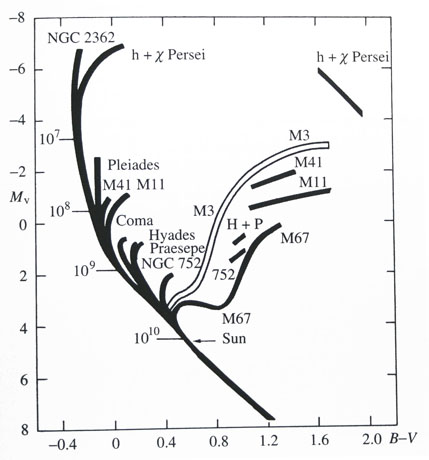
Diagramme HR d’un amas.Source : Fundamental astronomy, Karttunen
Le problème des magnitudes absolues est resté en suspend dans le second paragraphe, relatif à la construction d’un diagramme. Nous avons construit le diagramme sans connaître les magnitudes absolues, à partir des magnitudes apparentes, toutes définies par la même distance. Et nous avons obtenu un beau diagramme HR, avec une séquence principale bien dessinée. Quelle est la distance de l’amas ?
Ce n’est pas l’âge du capitaine !! Prenons un diagramme HR de référence, qui a été établi pour un amas de distance connue (proche, accessible à la méthode des parallaxes). Superposons les deux diagrammes. Le premier se trouve certainement ou trop haut, ou trop bas. Faisons-le glisser verticalement pour l’amener en correspondance avec l’autre. La quantité dont on le fait glisser correspond à la différence entre les magnitudes apparentes et absolues !! Et cette valeur est l’indicateur de distance. On vient de mesurer la distance de l’amas…
Considérons un amas d’étoiles assez lointain. La lumière qui nous parvient de lui traverse l’espace qui nous en sépare, et les nuages et poussières qu’il contient. Les interactions entre la rayonnement et la matière produisent un rougissement de la lumière. Comment évaluer la quantité de matière traversée ? Le diagramme HR nous donne évidemment la solution. Toutes les étoiles de l’amas subissent le même effet. Donc leur lumière est changée pareillement. Elle devient plus rouge. Prenant un diagramme HR normal, que devient-il si la lumière de toutes les étoiles devient plus rouge ? Le rouge est à droite sur le diagramme, le bleu à gauche. Un rougissement décale donc le diagramme, dans son ensemble, vers la droite. Et ceci d’autant plus que le rougissement est plus intense. Donc, si on constate un décalage entre le diagramme HR de cet amas et un diagramme normal, non rougi, l’écart entre les deux mesure le rougissement, donc la quantité de matière interstellaire traversée.
Lorsqu’on présente le diagramme HR, il est logique d’indiquer tout ce qu’on peut y trouver. Mais trouve-t-on vraiment tout dans un diagramme réel ? La réponse est souvent non.
Pour l’illustrer, considérons un amas d’étoiles qui vient de se former. Toutes les étoiles sont nées en même temps, quelle que soit leur masse. Considérons l’amas d’âge zéro, lorsque ses étoiles viennent d’arriver sur la Séquence Principale. Le diagramme HR correspondant contient la Séquence Principale complète. Mais il ne peut contenir aucune étoile plus évoluée, puisqu’elles n’en ont pas eu le temps. Pas de géantes rouges, pas de supergéantes, et a fortiori pas de naines blanches. Si vous voyez un diagramme d’amas qui ne contient que la Séquence Principale, c’est bien celui d’un amas d’étoiles jeune.
Plus tard, les étoiles les plus massives quittent la Séquence Principale, petit à petit, et leur évolution les mène vers la branche des géantes rouges, en passant par la zone des sous-géantes. On voit une chaîne d’étoiles partant de la SP et allant vers la branche des géantes. Corrélativement, la SP se trouve amputée de ses étoiles massives sur la gauche.
Plus tard encore, la branche des géantes est peuplée, la SP encore plus courte. Comme on l’a vu plus haut, la position du coude dans le diagramme HR indique l’âge de l’amas.
Le temps passant encore, les zones supérieures du diagramme se remplissent à mesure que la SP se dépeuple. Des supernovæ explosent, des étoiles moins massives se déplacent vers la gauche du diagramme en haut, puis descendent vers la zone des naines blanches en-dessous de la SP.
On pourrait imaginer que toutes les étoiles vont finir leur vie, et le diagramme ne plus montrer que des naines blanches. Mais ceci n’est pas possible pour deux raisons. La première est que les plus petites étoiles, celles en-dessous de quelques dixièmes de masse solaire, ont une durée de vie (sur la SP) plus longue que l’âge de l’Univers. Il ne peut donc y en avoir, et la SP ne peut jamais être totalement vide.
La seconde raison est que les phases avancées des amas ne peuvent pas s’observer pour les amas ouverts tels que les Pléïades, parce que la durée de vie de l’amas est inférieure au temps nécessaire pour cela. En effet, placées dans le disque galactique, les étoiles sont soumises aux perturbations des étoiles environantes. Et la rotation différentielle de la Galaxie n’arrange pas les choses, puisque les étoiles de l’amas les plus éloignées du centre tournent moins vite que les plus proches, et donc se laissent peu à peu distancer : l’amas s’effiloche.
---=OO=---