Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Trous noirs | |||||||
La notion de trou noir est aussi ancienne que la mécanique de Newton. Cependant, elle ne prend tout son sens que dans le cadre de la Relativité Générale, car les conditions qui règnent dans un tel objet ne sont pas compatibles avec les théories classiques. Sont-elles compatibles même avec la Relativité Générale ? Celle-ci a été élaborée pour des champs gravitationnels très forts, mais comme nous le verrons, l’horizon d’un trou noir marque la frontière de nos connaissances physiques.
En Relativité Générale, l’espace-temps est courbé par les masses. La masse d’une étoile, par exemple, déforme la géométrie de l’espace-temps autour d’elle. Une planète qui est lancée à son voisinage, suit une géodésique de l’espace-temps, c’est-à-dire une courbe de moindre action. Il se trouve que cette courbe est une ellipse, produite par la déformation. En fait, la planète suit exactement le même genre de ligne que s’il n’y avait pas d’étoile : elle poursuit son chemin par inertie (elle continue sur sa lancée). La seule différence est qu’en l’absence de masse, le chemin est droit, en présence de masse, il est courbe. Si l’espace-temps est déformé, elle en suit les déformations.
Ainsi, toute particule lancée dans l’espace-temps suivra les géodésiques de l’espace, qu’elle soit massive ou non ! C’est ainsi qu’un photon, de masse nulle, sera dévié de la même manière qu’une étoile. On possède aujourd’hui de multiples preuves observationnelles de cette affirmation.
Un trou noir est un objet dont la gravité est assez forte pour empêcher la lumière (et toute forme de matière) d’en sortir.
En mécanique classique, on définit la vitesse de libération, qui est la vitesse nécessaire pour s’échapper de la surface d’un astre. Celle-ci dépend de la masse et du rayon de ce dernier. Si on augmente la masse, la vitesse de libération augmente aussi. Elle peut ainsi atteindre la vitesse de la lumière. C’est ainsi que les trous noirs ont été imaginés d’après la théorie de Newton, par Mitchell et Laplace.
Faisons un calcul classique : l’énergie cinétique d’un corps tombant sur un trou noir est Ec = 1/2 m v2. Si v = c (vitesse de la lumière, vitesse limite) alors : Ec = 1/2 m c2.
. Or l’énergie totale Etot = Ec + Ep = 0, puisqu’il n’y a pas d’échange d’énergie avec l’extérieur. Or l’énergie potentielle est Ep = -G M m / Rs. Donc 1/2 m c2 - G M m / Rs = 0. D’où :Rs est le rayon de Schwarzschild. C’est la distance au centre du trou noir en-deça de laquelle la vitesse de libération dépasse la vitesse de la lumière.
En calculant la constante 2 G / c2 dans les bonnes unités, on obtient Rs = 1,483 10-30 km kg-1 M. Cette expression est plus pratique, puisque déjà en partie calculée. Mais elle nécessite de donner la masse de l’objet en kilogrammes, ce qui n’est pas très habituel. Calculons le rayon de Schwarzschild du Soleil :
M = 2 1030 kg donc Rs = 1,483 10-30 km kg-1 × 2 1030 kg = 2,97 km. C’est la valeur habituellement donnée, arrondie à 3 km.
Calculons maintenant le rapport Rs / Rs = (2 G M / c2) / (2 G M / c2) = M / M
Donc Rs = Rs (M / M) = 3 km (M / M)
Ici, M / M représente la masse de l’objet en unités de masse solaire. Donc le rayon de Schwarzschild s’écrit tout simplement :
M étant donnée en masses solaires, et le résultat étant obtenu en kilomètres.
Si on choisit M = 1M, on retrouve bien 3 km.
Pour un trou noir de 3 millions de masses solaires, comme celui qui se trouve au centre de la Voie Lactée, on trouve 9 millions de km. Valeur à rapprocher des 50 millions de km, distance moyenne de Mercure au Soleil.
Déduite ci-dessus par les moyens de la mécanique classique, la formule du rayon de Schwarzschild est la même en Relativité Générale. Tant qu’on se trouve en-deça du rayon de Schwarzschild, on peut dire, toujours avec un raisonnement classique, qu’aucun objet matériel ne peut s’échapper d’un tel astre, puisqu’il lui faudrait pour cela aller plus vite que la lumière (on utilise pour le dire, le principe fondateur de la Relativité Restreinte, attesté par l’expérience).
En faisant le raisonnement correct en Relativité Générale, la masse du trou noir déforme l’espace-temps à l’entour, et tout mobile suit dans cet espace-temps une géodésique. Les photons suivent la règle générale et, bien que sans masse, sont influencés par le trou noir. Mais il y a une différence fondamentale entre matière et rayonnement ici. Pour qu’un élément matériel s’échappe du trou noir, il faut qu’il se déplace, à l’opposé du centre, à une vitesse supérieure à la vitesse de libération. Pour que ce soit possible, il faut qu’il soit au départ au-delà du rayon de Schwarzschild. Par contre, un rayon lumineux se déplace toujours à la vitesse de la lumière. Le voisinage du trou noir ne change rien à cela. Mais dans un champ très intense, l’énergie du rayonnement e = h ν diminue. Par conséquent, sa fréquence ν diminue également. Il devient donc plus rouge. Sa fréquence tend donc vers 0, valeur qui est atteinte à l’horizon du trou noir. Toute lumière émise à l’horizon du trou noir a donc une longueur d’onde infinie, et semble complètement figée. Le temps est arrêté pour un observateur extérieur.
Pour comprendre comment l’espace-temps est courbé à proximité d’un trou noir, il est peut-être plus simple de suivre comment un astre s’effondre. Le schéma ci-dessous, dû à Jean-Pierre Luminet, montre les étapes de l’effondrement d’une étoile massive en trou noir. Partant d’une situation dans laquelle l’espace-temps est à peine déformé (donc pratiquement euclidien, en haut et à gauche), l’effondrement de l’objet produit une courbure de plus en plus forte autour de lui.
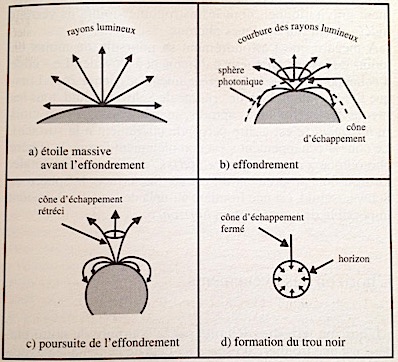
Au début, tous les rayons émis depuis un point, au-dessus du sol c’est-à-dire dans un cône de 180° d’ouverture, peuvent parvenir à un observateur extérieur.
Deuxième schéma. Lorsque la gravité augmente, les rayons émis tangentiellement à l’astre, au raz du sol, sont courbés, et rencontrent la surface. Ils sont les premiers à disparaître à un observateur extérieur. Le cône dont la lumière peut s’échapper a un angle un peu inférieur à 180°.
Troisième schéma. La gravité augmentant, des rayons émis plus près de la verticale se retrouvent suffisamment courbés pour retomber sur l’astre. Le cône de lumière visible de l’extérieur a encore diminué, et son angle est bien plus petit que 180°.
Quatrième schéma. Lorsque l’astre est totalement effondré, le cône de lumière visible s’est complètement refermé. Tous les rayons lumineux émis pas l’astre sont assez courbés pour rencontrer sa surface. Ainsi, aucun ne parvient à l’extérieur.
Toute information étant piégée à l’intérieur du trou noir, il est impossible de savoir ce qu’il se passe en son sein. Impossible en particulier de connaître la répartition de la matière en fonction du rayon (est-elle concentrée en une vraie singularité au point central ?). Donc, on ne peut pas définir la masse volumique en fonction de la distance au centre, comme on le ferait pour un astre ordinaire. La seule mesure possible est celle de la masse volumique moyenne, qui est simplement le rapport de la masse au volume.
La masse volumique moyenne d’un objet est définie par : ρ = M / V = M / (4/3 π R3) = 3 M / 4 π R3
Remplaçons R par Rs :
ρ = 3 M / 4 π Rs3 = 3 M / 4 π (2 G M / c2)3 = 3 M c6 / 4 π 8 G3 M3 = (3 c6 / 32 π G3) M-2
Le facteur 3 c6 / 32 π G3 est constant. Si on définit k = 3 c6 / 32 π G3, il vient :
Cette petite démonstration détruit l’idée reçue selon laquelle un trou noir est un objet exceptionnellement dense (la densité est le rapport de la masse volumique d’un corps à celle de l’eau, qui est de 1 g cm-3). Si sa masse est faible, en effet il aura une grande densité. Par exemple, si le Soleil se transformait en trou noir (mais ceci n’est pas son destin), sa masse volumique serait :
ρ = (3c6 / 32 π G3) / M2
Il faut exprimer toutes les valeurs dans des unités cohérentes, par exemple cm, g et s.
c = 300.000 km s-1 = 3 105 km s-1 = 3 1010 cm s-1
G = 6,6726 10-11 m3 kg-1 s-2 = 6,6726 10-5 cm3 kg-1 s-2 = 6,6726 10-8 cm3 g-1 s-2
M = 1,9891 1033 g
Alors, ρ se calcule ainsi :
ρ = 3 × (3 1010)6 / 32 π (6,6726 10-8)3 (1,9891 1033)2 = 3 × 729 1060 / 100,53 × 297 10-24 × 3,956 1066 = 2187 1060 / 118115,9 1042 = 1,85 10-2 1060 10-42
ρ = 1,85 1016 g cm-3 soit presque 20 milliards de tonnes par cm3.
Faisons le rapport entre la masse volumique d’un trou noir quelconque et celle d’un trou noir d’une masse solaire :
ρ / ρ = M-2 / M-2 = (M / M)-2 ; donc ρ = ρ (M / M)-2 = 1,85 1016 g cm-3 (M / M)-2
M / M représente la masse du trou noir par rapport à celle d’un trou noir d’une masse solaire ; c’est donc la masse de ce trou noir en unités de masse solaire. Par suite :
ρ est obtenu en g cm-3, M étant exprimée en masses solaires. Ci-dessous, le tableau donne le rayon de Schwarzschild et la masse volumique de quelques trous noirs, obtenus d’après les formules ci-dessus :
| Masse en M | rayon de Schwarzschild en km | Masse volumique en g cm-3 |
|---|---|---|
On voit qu’un trou noir d’un milliard de masses solaires est 100 fois moins dense que l’eau…
Vous pouvez ici calculer ces valeurs pour toute masse, exprimée en masses solaires (à gauche), ou en kilogrammes (à droite) :
| Masse | rayon de Schwarzschild en km | Masse volumique en g cm-3 | |
|---|---|---|---|
| en M | en kg | ||
Donnez la masse du trou noir (en notation française !). Pour les grandes masses, utilisez la notation scientifique, par exemple 2,8e+6 pour 2,8 millions de masses solaires (masse approximative du trou noir central de la Voie Lactée).
Si vous voulez calculer le rayon de Scharzschild d’un objet moins massif, vous pouvez exprimer sa masse en kg. Le rayon est alors donné en cm.
La formidable gravité d’un trou noir dévie les rayons lumineux qui passent à proximité, et produisent des mirages vraiment extraordinaires. Une page leur est consacrée.
On s’en serait douté ! Mais en fait, cette expression imagée dit qu’un trou noir est un objet bien monotone. Un trou noir est en effet entièrement caractérisé par trois paramètres, pas un de plus : sa masse, sa charge électrique, et sa vitesse de rotation. Que vous le regardiez (au moins avec les yeux de la théorie) d’un côté ou de l’autre, vous voyez exactement la même chose. Rien à voir avec la diversité de la Terre par exemple ; la gravité gomme tout.
Les autres objets sont en équilibre par l’action de plusieurs forces distinctes, qui se complètent ou se contrarient.
Un trou noir ne connait que la gravité.
Chandrasekhar disait que le trou noir est l’objet macroscopique le plus simple qui soit, et aussi le plus parfait !
Les trous noirs dont nous avons parlé jusqu’ici n’étaient pas en rotation, et n’avaient pas de charge électrique. Nous verrons plus loin qu’un trou noir doit tourner, et sera un peu plus complexe que ce que nous venons de dire.
On doit faire une grande différence entre l’existence des trous noirs, et leur formation. Parler de leur formation consiste à envisager un mécanisme pour faire passer une quantité de matière donnée, de l’état normal à l’état de trou noir. Or un tel mécanisme peut ne pas exister aujourd’hui. Prenons par exemple une étoile en fin de vie, dont le cœur après expulsion de l’enveloppe, a une masse de 1 M. Lorsque l’énergie de fusion y est épuisée, plus rien ne s’oppose à la gravité, et l’étoile s’effondre. Mais pendant l’effondrement se crée une pression de Fermi des électrons, assez forte pour l’arrêter. Cette masse ne deviendra donc pas un trou noir.
Si la masse du cœur est comprise entre 1,4 et 3 M, ce sont les neutrons qui arrêteront l’effondrement (par le même mécanisme de Fermi), l’objet devenant une étoile à neutrons. Ce n’est qu’au-dessus de 3 M qu’un trou noir stellaire (formé à partir d’une étoile) peut se produire.
Pour qu’il se produise effectivement, il faut donc que la masse soit supérieure à 3 M. Or les étoiles massives perdent la plus grande partie de cette masse dans leur évolution, et peut-être descendent-elles toutes en-dessous de la masse nécessaire pour former un trou noir ? Non, car les observations montrent le contraire. La source X Cygnus X-1 est en effet un système binaire émettant dans les rayons X. Il est constitué d’un objet autour duquel orbite l’étoile HD 226868. La période de révolution de cette étoile, mesurée à 5,6 jours par le satellite Uhuru, permet d’assigner à l’autre objet une masse d’au moins 6 M. Une détermination ultérieure [J.A. Orosz 2011] bien plus précise indique 14,8 ± 1 M. HD 226868 est une supergéante de masse 19,2 ± 1,9 M, qui remplit son lobe de Roche et dont la matière, en tombant sur le trou noir, produit le rayonnement.
Ainsi, les trous noirs stellaires existent bel et bien, mais seulement pour une masse supérieure à 3 M.
Il existe un autre mécanisme permettant d’arriver à un trou noir pas suite de l’évolution stellaire. C’est en passant par une naine blanche ou une étoile à neutron. L’une ou l’autre peut, si elle est en orbite autour d’un compagnon emplissant son lobe de Roche, recevoir de la matière et augmenter sa masse. Mais tant que celle-ci reste au-dessous de 3 M, les neutrons développent la pression de Fermi et empêchent la formation d’un trou noir. Ce n’est que lorsque la masse dépasse la limite fatidique de 3 M que l’effondrement se produit. Que ce soit donc directement ou indirectement, le trou noir produit a une masse au-dessus de cette limite.
Pour des masses inférieures, aucun mécansime ne peut, dans les conditions physiques actuelles dans l’univers, faire passer la matière dans l’état trou noir.
Il semble qu’il y ait, au centre de chaque galaxie ou presque, un trou noir plus ou moins massif. De récentes observations du centre de notre Voie Lactée le confirment, par le mouvement d’une étoile très proche. On peut voir ici l’orbite décrite par l’étoile S2 autour d’un trou noir de 2,6 millions de masses solaires.
Les données actuelles donnent à penser que toutes les galaxies (presque) sont passées par l’état de quasar lorsque suffisamment de gaz se trouvait dans les régions centrales pour alimenter le trou noir. Les collisions entre galaxies peuvent réalimenter un quasar endormi, des observations le montrent.
L’existence des trous noirs galactiques, dont la masse atteint des millions de masses solaires, est donc bien assurée.
Faisant l’impasse sur le mode de formation, on peut effectivement envisager l’existence de trous noirs de toutes masses, mais à la condition que dans le passé, un mécanisme ait pu les créer. C’est pourquoi on parle de trous noirs primordiaux. Lorsque l’Univers était très dense, peu après le Big Bang, il est possible que des fluctuations quantiques aient permi la formation de trous noirs de faible masse. Leur diamètre serait absolument minuscule, puisqu’un trou noir d’une masse terrestre ne ferait qu’un centimètre de diamètre ! Pour une masse comparable à celle du massif du Mont Blanc, le diamètre du trou noir serait comparable à celui d’un atome…
De si petits trous noirs ne pourraient rayonner par accrétion de matière, ou si faiblement qu’ils seraient totalement indétectables de cette manière. D’autre part, leur faible masse produirait des perturbations insignifiantes sur les autres astres, dont les mouvements ne permettraient pas de les détecter. Par conséquent, aucune indication observationnelle n’en atteste l’existence, mais rien ne permet de d’infirmer.
Ce sont des trous noirs de masse intermédiaire entre les deux types précédents, et produits par l’évolution des étoiles (soit seule, après épuisement des sources d’énergie, soit par échange de matière). Ceux-là existent bien, comme l’indiquent les observations dans les rayonnements énergétiques, X ou gamma.
La métrique est l’expression de la mesure de l’intervalle entre deux événements infiniment voisins de l’espace-temps. Elle décrit comment on passe d’un point à un point très proche, en fonction des masses en présence (qui déforment l’espace-temps, déformations que traduit la métrique). Dans les explications données jusqu’ici, on a considéré un trou noir sans rotation, parfaitement sphérique. Sans rotation, l’espace-temps est isotrope autour du centre du trou noir : toutes les directions sont semblables. Cette grande simplification a permis d’établir une métrique simple, nommée métrique de Schwarzschild. Le trou noir ainsi décrit est naturellement sphérique.
Mais dans l’univers, rien n’est parfaitement fixe, et les objets tournent toujours. Avec la conservation du moment cinétique, un astre tournant qui s’effondre accélère considérablement sa vitesse de rotation. Un trou noir formé par effondrement d’une étoile massive par exemple, doit donc tourner, et même très, très vite. S’il tourne, il possède un axe de rotation, qui est un axe de symétrie, et il doit présenter un aplatissement. Donc, il n’a plus la symétrie sphérique, et la métrique de Schwarzschild ne convient plus pour le décrire. Il faut en définir une nouvelle.
Pour décrire un trou noir en rotation, Roy Kerr a donc défini une métrique axisymétrique. Partant de la forme la plus générale, et imposant des conditions qui doivent être remplies par un trou noir en rotation, on aboutit à la métrique de Kerr. La métrique obtenue montre un phénomène inconnu jusqu’alors, l’entraînement du référentiel (effet Lense-Thirring découvert par Josef Lense et Hans Thirring, physiciens autrichiens, ou frame-dragging).
Considérons une masse qui tomberait sur le Soleil, lâchée depuis l’orbite de Pluton, mais sans vitesse initiale (sans tourner autour du Soleil). Cette masse tomberait tout droit, c’est-à-dire radialement. Approchant du Soleil, sa vitesse augmenterait, mais sa trajectoire resterait rectiligne.
Considérons maintenant une même masse, mais lâchée au-dessus d’un trou noir de Kerr (en rotation). Auprès d’un tel corps, les géodésiques subissent naturellement la courbure gravitationnelle, mais de plus, elles sont entraînées dans la rotation, un peu comme si des frottements se produisaient. Et la masse se met à tourner autour du trou noir, dans le sens de sa rotation. Dans un disque d’accrétion, ce phénomène amplifie donc la rotation naturelle de la matière qui tombe.
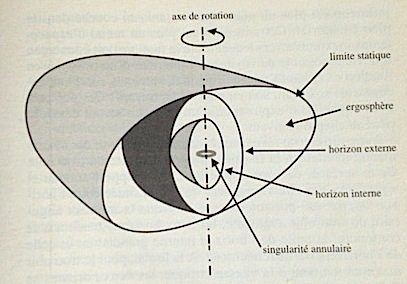
Alors qu’un trou noir de Schwarzschild est simple, la rotation d’un trou noir de Kerr entraîne une complexité déroutante. La métrique montre qu’il n’y a plus un horizon des événements, mais deux ! La singularité centrale n’est plus un point, mais un anneau… Et pour que ce soit plus amusant, il existe une nouvelle limite, nommée limite statique, extérieure à l’horizon des événement (le plus externe). Entre cet horizon et la limite statique, rien ne peut rester immobile. Le mouvement est obligatoire, et c’est de là que vient le nom de limite statique.
On voit sur le schéma que l’anneau singulier, l’horizon interne et l’horizon externe sont emboîtés strictement, sans points de contact. Par contre, l’horizon externe est bien à l’intérieur de la limite statique, mais il lui est tangent aux pôles.
La limite statique et l’horizon externe se partagent le rôle de l’horizon unique d’un trou noir de Schwarzschild. La limite statique est celle où le temps s’arrête, pour un observateur extérieur. C’est aussi celle où la décalage spectral gravitationnel vers le rouge devient infini. Ces propriétés sont celles de l’horizon du trou noir de Schwarzschild. Mais de plus, on ne peut pas ressortir d’un trou noir de Schwarzschild dès qu’on a passé l’horizon. Par contre, on peut encore sortir d’un trou noir de Kerr après avoir franchi la limite statique, masi pas encore l’horizon externe.
La limite statique du trou noir de Kerr correspond à une zone dans laquelle les possibilités de navigation sont restreintes, mais dont on peut toujours s’échapper. Reprenons l’analogie donnée par Jean-Pierre Luminet : un maelström marin est une zone où la mer se creuse en tournant de plus en plus vite quand on s’approche du centre. Si un bateau, capable de filer 37 km/h (20 nœuds…), navigue au loin, il est libre d’aller dans toutes les directions. Mais s’il s’approche jusqu’à la zone où le maelström tourne à 37 km/h, commence à se poser un problème : il ne pourra plus aller à contre-sens car, au mieux il resterait immobile (naviguant à 37 km/h sur une eau qui file dans l’autre sens à 37 km/h). Il est déjà privé d’une direction, mais il lui reste les autres. S’il se laisse emporter par le courant (en tournant dans le même sens), il peut utiliser sa vitesse propre pour s’éloigner du centre, et échapper au maelström.
S’il s’approche davantage, il risque d’atteindre une zone où l’eau s’engouffre dans le tourbillon à plus de 37 km/h. Alors, tous ses efforts seront vains, il ne pourra plus en sortir.
Entre ces deux zones, il peut s’échapper en empruntant une trajectoire en spirale, qui l’éloigne peu à peu du centre… à condition bien sûr d’avoir assez de carburant !La première limite correspond à la limite statique. En-dessous, la liberté du navigateur diminue lorsqu’il s’approche du centre. La seconde limite est celle au-delà de laquelle il a perdu toute liberté, et ne peut plus lutter contre l’entraînement. Il ne pourra plus sortir ; c’est l’horizon. Il suffit de remplacer la vitesse du bateau par celle de la lumière pour obtenir une image d’un trou noir en rotation.
La zone située entre la limite statique et l’horizon se nomme ergosphère. Ce nom bizarre vient du grec ancien εργοσ = travail. Nous venons de dire que l’on pouvait s’extraire de cette zone. Par conséquent, il serait possible aussi d’en extraire de l’énergie, puisqu’on peut franchir la limite statique (pas n’importe comment). Le nom signifie donc qu’on pourrait tirer un travail de cette zone, pris sur la rotation du trou noir.
La singularité d’un trou noir sans rotation est un point qui attire tout ce qui l’approche. Mais dans un trou noir de Kerr, la singularité devient un anneau équatorial, et tout change. Il devient possible à une particule de le survoler sans y aboutir inéluctablement. Vraiment incroyable quand on connait les propriétés des trous noirs simples…
Quelle est la proportion de trous noirs de Schwarzschild, et de trous noirs de Kerr, parmis ceux qu’on a effectivement découverts dans l’univers ? La réponse est simple : 0 % de trous noirs de Schwarzschild… Bizarre ? Absolument pas. Les trous noirs que l’on observe sont le résultat de la contraction d’une étoile (au moins pour les moins massifs d’entre eux). Or les étoiles sont en rotation, et la conservation du moment angulaire, au moment de l’effondrement, l’accélère. Impossible donc d’imaginer un trou noir qui ne tourne point. Il est plus difficile de savoir comment se sont formés les trous noirs supermassifs placés au centre des galaxies. Mais il est fort probable qu’ils sont aussi en rotation. C’est donc le modèle de Kerr qui est pertinent.
Mais quand on considère un astre non effondré, le problème de la rotation est bien moins pressant. Pour le Soleil par exemple, sa vitesse de rotation est si faible que l’effet d’entraînement de l’espace-temps est bien négligeable. Par conséquent, la métrique de Schwarzschild est parfaitement applicable pour décrire l’espace-temps en son voisinage.
• Une propriété surprenante des trous noirs de Kerr concerne la gravité à la surface, c’est-à-dire à l’horizon des événements. En tout point de l’horizon, la gravitation a la même valeur, rigoureusement. Si on considère un astre non effondré, comme Jupiter par exemple, on montre que la gravité aux pôles est plus forte qu’à l’équateur. Ceci tout simplement parce que le rayon y étant plus faible, la gravité est plus élevée. Mais un trou noir est entièrement gouverné par la gravitation, les forces électriques n’intervenant plus. C’est en fait la complexité due à toutes les forces en présence qui modifie la gravitation dans un astre non effondré.
Cette propriété est curieuse, si on la met en parallèle avec le premier principe de la thermodynamique. Celui-ci énonce que, dans un corps en équilibre thermique, tous les points sont à la même température. C’est sans doute une coïncidence…
• Considérons deux trous noirs de masse égale, m. Le rayon de Schwarzschild vaut rs = 2 G m / c2. Il est proportionel à m, ce qu’on écrit : rs ∝ m. La surface de l’horizon est s = 4 π rs2. Elle est proportionelle au carré du rayon de Schwarzschild, ce qu’on écrit : s ∝ rs2. Donc s ∝ rs2 et rs ∝ m ⇒ s ∝ m2.
Si ces deux trous noirs fusionnent, le résultat sera un trou noir de masse M = 2 m. Sa surface sera donc S ∝ M2, donc S ∝ (2 m)2 = 4 m2. Et donc S = 4 s (on peut mettre l’égalité, car la constante est la même pour ses deux membres).
La surface du trou noir résultant est donc 4 fois supérieure à celle de ses constituants. Ce résultat est à revoir un peu, car lors de leur fusion, deux trous noirs tournent l’un autour de l’autre, déformant l’espace-temps de façon dynamique. Ceci émet des ondes gravitationnelles, dont l’énergie est prise au système. Le trou noir résultant a une masse inférieure à la somme des masses, la différence étant l’énergie gravitationnelle rayonnée. Mais ceci ne remet pas en cause la conclusion, que l’aire d’un trou noir croît avec sa masse. En effet, pour que la masse du trou noir formé soit égale à m, il faudrait que 50 % de la masse du couple soit rayonnée. Or cette valeur est bien le maximum envisageable, dans des condition bien particulières loin d’être réunies ici.
Comme pour la première propriété, on remarque une analogie avec l’entropie ; l’entropie d’un système isolé ne peut que croître au cours du temps - l’aire d’un trou noir ne peut que croître au cours du temps.
Cette seconde analogie a provoqué des études plus poussées. Et le résultat est que l’on peut parler aujourd’hui de la thermodynamique d’un trou noir.
Une vérification de cet effet a été tentée par un satellite américain, Gravity Probe B, lancé en 2004 pour deux ans de service. La conception du satellite est très délicate, il s’agissait de fabriquer des gyroscopes un million de fois plus précis que ce qu’on avait fait auparavant. Ensuite, il a fallu analyser les résultats, ce qui s’est avéré aussi très difficile. Il semble que l’effet Lense-Thirring ait été confirmé, mais tout le monde n’est pas d’accord sur ce résultat.
J.A. Orosz, The Mass of the Black Hole in Cygnus X-1, Arxiv 2011
Des quasars aux trous noirs, Suzy Collin-Zhan, 2009
Active Galactic Nuclei, Julian Krolik, 1999
Les trous noirs, Jean-Pierre Luminet, 1992
---=OO=---