L’actualité du LAM	Le cours à l’Observatoire Historique de Marseille	… …	liens - alphabet grec bibliographie fiches lexique multiplicateurs tableau périodique	Mis à jour le 18/08/17
Modèles stellaires

Pour résoudre le problème de la structure stellaire, on considère l’étoile en deux parties : le cœur et l’enveloppe. On peut étudier les deux séparément, alors qu’ensemble le problème serait trop complexe. Dans l’étude de chaque partie, on ignore donc les contraintes dues à l’autre. Cette absence de contraintes permet d’avoir, pour chaque partie, beaucoup plus de solutions. On obtient donc beaucoup de solutions pour le cœur, et beaucoup d’autres pour l’enveloppe.

Si on choisit arbitrairement une solution pour chaque partie, on risque fort qu’elles soient incompatibles : par exemple, la pression à l’interface entre le cœur et l’enveloppe serait très différente dans les deux solutions, alors qu’elles s’appliquent au même endroit de l’étoile. Il faut donc prendre en compte les contraintes réciproques, qui nous donneront des solutions compatibles.

Première approche

Limite de Schönberg-Chandrasekhar

C’est la masse maximale d’un cœur d’étoile massive, en équilibre thermique. Pour la déterminer, on reprend l’expression de la pression à la surface d’une étoile, qu’on a vue en étudiant l’effondrement d’un nuage. Mais on la précise et on l’adapte au cœur de l’étoile :

P₀ = a T₀ M_c/ R_c³ - b M_c²/ R⁴

R_c et M_c sont le rayon et la masse du cœur. T₀ est la température du cœur. A la surface du cœur, la température de l’enveloppe est égale à T₀. La température du cœur est pratiquement constante, puisqu’il est chauffé de l’extérieur par la fusion de l’enveloppe. Donc la température à la base de l’enveloppe est elle aussi constante.

La pression à la surface du cœur dépend uniquement de la masse du cœur, et non de la masse de l’étoile. Comme nous l’avons vu pour un nuage en contraction, la présence de ces deux termes entraîne l’existence d’un maximum pour la pression : pour une masse du cœur donnée M_c, il existe un rayon R_c pour lequel la pression à la surface est maximale. Il en est de même ici.

On trace la courbe représentant la pression en fonction de la masse du cœur :

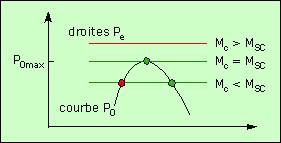
Courbe de la pression à la surface du cœur

Un calcul très simple donne la pression maximum (c est une constante)  :

P_{0 max} = c T₀⁴ / M_c²

Considérons maintenant l’enveloppe du cœur. On montre que sa pression est de l’ordre de Pe = M² / R⁴, et sa température Te = M / R = T₀. Puisque cette température est constante (voir plus haut), M / R l’est aussi. Alors :

T₀⁴ = M⁴ / R⁴

et en divisant par M_c² :

T₀⁴ / M² = M² / R⁴

Le second membre de cette égalité représente la pression Pe. Donc :

Pe = M² / R⁴ = T₀⁴ / M²

Pe = T₀⁴ / M²

T₀ et M étant constants, Pe l’est aussi. Donc la courbe qui représente la pression de l’enveloppe est une droite horizontale. On la place dans le schéma, mais sa hauteur dépend de la masse totale M de l’étoile, alors que la pression à la surface du cœur dépend de la masse du cœur. On ne sait donc pas a priori à quelle hauteur placer la droite. Trois positions caractéristiques sont possibles, et à considérer :

• la droite est au-dessus du maximum de la courbe. La pression de l’enveloppe est supérieure à celle de la surface du cœur (au même point donc). L’étoile ne peut pas être en équilibre.
• la droite coupe la courbe en deux points différents. En ces deux points, les pressions sont donc égales, et pourraient donner des solutions. Mais le point de gauche est instable : si on diminue légèrement le rayon du cœur, sa pression diminue (elle varie dans le même sens que le rayon). Donc la pression de l’enveloppe devient prépondérante, et le cœur s’effondre. Cette solution n’est pas en équilibre. Le point de droite par contre montre un équilibre stable, qui donne une solution valable. En effet, une légère compression entraîne une augmentation de la pression du cœur, qui bloque la compression. La pression varie en sens inverse du rayon, donc elle s’oppose à ses variations.
• enfin, la droite peut se placer dans la position particulière qui correspond au maximum de la courbe : cet équilibre est stable

Le principe du calcul est donc simple :

• on trace la courbe de la pression du cœur en fonction du rayon du cœur ;
• on trace des droites qui représentent la pression de l’enveloppe en fonction du rayon du cœur également ;
• on détermine les valeurs pour lesquelles l’équilibre est stable.

On peut faire une autre remarque : la pression maximum varie comme 1 / M_c².

P_{0 max} = c T₀⁴ / M_c²

trois fragments

Les nombreuses recherches sur la structure des étoiles ont permis de produire un ensemble de modèles qui représentent assez bien les diverses étapes de la vie d’une étoile.

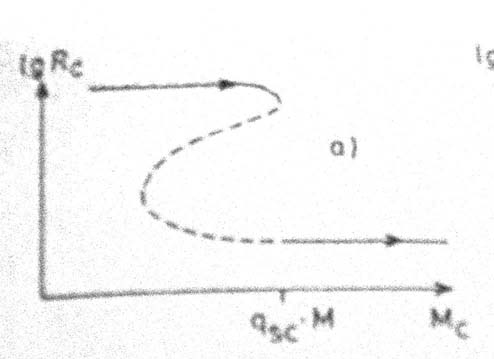
Ce schéma montre comment évolue le cœur d’une étoile, pendant la fusion de l’hydrogène, puis de l’hélium. En abscisse, on trouve la masse du cœur, et en ordonnées le logarithme du rayon.

La courbe montre trois fragments, deux en traits pleins et un en pointillés. Les traits pleins indiquent la stabilité thermique de l’étoile, les pointillés son instabilité.

L’arc supérieur correspond aux étoiles naines, de la Séquence Principale. L’arc inférieur correspond aux géantes. Entre les deux, l’étoile évolue en déséquilibre thermique.

L’équilbre thermique ne doit pas être confondu avec l’isothermie ! Il signifie qu’il n’y a pas d’évolution au cours du temps, qu’en chaque point la température de l’étoile reste la même. Mais l’isothermie signifierait que la température soit la même en tous points !

La courbe montre tout d’abord que pendant la fusion, la masse du cœur de l’étoile augmente : à mesure que l’hydrogène (ou l’hélium dans la branche inférieure) se transforme, le cœur devient inerte. La fusion se propage vers l’enveloppe, qui vient accroître la masse du cœur.

Même si cette augmentation de masse s’accompagne d’une contraction, la masse relative (m/M) ne fait qu’augmenter. En ce sens, le cœur grossit.

Sur la branche supérieure, qui correspond à la fusion de l’hydrogène, on voit le cœur grossir (en masse relative) à rayon constant (puisque la courbe est horizontale). Ceci se produit pendant toute la durée de la fusion de l’hydrogène dans le cœur. On le comprend bien si on se souvient que le cœur d’une étoile massive est convectif ; la matière est mélangée, donc la fusion se produit dans la même zone jusqu’à épuisement de l’hydrogène.

Sur le graphique, on voit alors une courbe vers le bas qui s’amorce. Il faut expliquer cette modification : la masse du cœur continue d’augmenter, mais le rayon du cœur diminue.

---=OO=---