Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Effondrement et fragmentation d’un nuage | |||||||
On considère un immense nuage d’hydrogène, comme il en existe beaucoup dans une galaxie spirale encore aujourd’hui.
Dans ce nuage, on va étudier une partie sphérique (sphérique par soucis de simplification), qui subit une légère perturbation extérieure. Une telle perturbation pourrait provenir de l’explosion d’une supernova à proximité du nuage. Toujours pour simplifier, on va supposer que la perturbation agit sur toute la surface de la sphère.
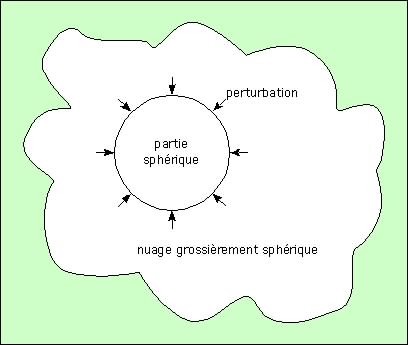
Ces conditions paraissent fortes, mais les résultats que l’on en déduira seront tout de même représentatifs. De nombreux travaux ont été effectués dans ce domaine, avec des contraintes différentes, et les résultats convergent vers des valeurs du même ordre de grandeur. Il est bien sûr impossible de s’attaquer à un problème réel, qui nécessiterait une connaissance du milieu (état initial du nuage) tout à fait hors de notre portée. La théorie présentée ici n’est pas celle construite par Jeans, mais une version plus simple dont les résultats sont du même ordre de grandeur.
L’idée de base est que la matière qui commence à s’effondrer transforme l’énergie potentielle en énergie cinétique dans sa chute. Cette énergie cinétique produit un échauffement, donc une pression, qui contrecarre la chute. Il est donc naturel d’envisager un équilibre.
La partie du nuage extérieure à la sphère n’a aucune influence gravitationnelle sur elle, si nous lui supposons aussi la symétrie sphérique, condition raisonnable dans un nuage assez grand.
Nous allons considérer que le nuage est constitué d’un gaz parfait, ce qui est parfaitement légitime dans les conditions physiques qui y règnent.
La surface de la sphère considérée est soumise à une pression P non nulle, puisqu’elle se trouve incluse dans un nuage de densité non nulle.
Enfin, elle est isotherme : la température à l’intérieur d’un tel nuage est la même partout ; elle est de l’ordre de 100 K dans les nuages d’hydrogène atomique, et de 10 K seulement dans les nuages moléculaires. De plus, la densité est si faible que, même après une assez forte contraction, le nuage restera suffisament dilué pour être transparent, et laisser échapper l’énergie produite en son sein. Dans ces conditions, sa température n’augmentera pas, et la transformation se fera à température constante. On dit qu’elle est isotherme.
Soit R le rayon de la sphère considérée.
Un calcul assez simple montre que la pression P0 à la surface de la sphère est de la forme (que nous admettrons) :
Le premier terme représente la pression du gaz (qui pousse le gaz vers l’extérieur) , le second l’autogravitation du nuage (qui l’attire vers le centre). a et b sont des constantes positives dépendant de la masse de la sphère et de sa température. Le premier terme est positif, le second négatif. Puisqu’ils font intervenir R à des puissances différentes, l’un varie plus vite que l’autre.
Il est très simple d’étudier la variation de P0 en fonction du rayon. Elle est visualisée sur le schéma suivant :
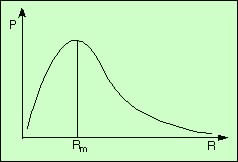
La courbe présente un maximum, atteint pour une valeur Rm du rayon. Ceci a une importance capitale pour la stabilité du nuage.
N’oublions pas que :
La sphère est en équilibre, avec la pression superficielle P0. Deux cas se présentent :
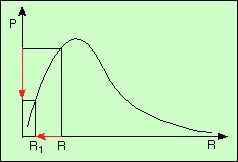
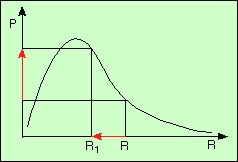
Par conséquent, la perturbation s’amplifie en effondrement si le rayon est plus petit que Rm, et s’amorti sinon.
On calcule que :
(Rm correspondant au maximum de P, il suffit de calculer la dérivée de P par rapport à R, et d’écrire qu’elle est nulle)
k est une constante, T la température du nuage, et ρ sa masse volumique.
L’effondrement a lieu pour R < Rm, donc si :
Tm et ρm correspondent au rayon maximum.
La contraction du nuage étant isotherme (voir au début de cette page), T = Tm. On peut simplifier, et :
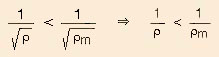
et en inversant la relation :
L’effondrement se produit donc pour une masse volumique supérieure à la masse volumique critique (celle correspondant au rayon maximum). Il se produit donc pour une masse supérieure à une limite que l’on nomme masse de Jeans.
Le problème a été très simplifié ici, pour des raisons évidentes de compréhension. Mais des calculs beaucoup plus précis ont été faits par de nombreux auteurs, et leurs résultats convergent vers le même ordre de grandeur. Aussi, ces résultats sont valides à un petit facteur près.
La masse de la sphère est égale à son volume, multiplié par sa masse volumique :
M = 4/3 π R3 ρ
En remplaçant R par la valeur de Rm trouvée plus haut, on obtient la forme de la masse de Jeans :
Mj = k′ T3/2 ρ-1/2
La masse de Jeans pour un nuage d’hydrogène est prise égale à :
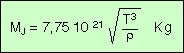
T doit être exprimée en Kelvins, et ρ en kg/m3. Le coefficient a été obtenu à partir d’une théorie beaucoup plus détaillée que le simple calcul ci-dessus.
Pour un nuage normal, de température comprise entre 10 et 100 K, et de densité autour de 1.000 atomes par cm3, on obtient une masse de Jeans de l’ordre de 105 M. Cette valeur est beaucoup plus grande (1.000 fois au moins), que la masse d’une étoile. Donc l’effondrement d’un nuage de ce genre ne peut pas produire directement une étoile !
Nous allons maintenant déterminer le temps de contraction du nuage. Puisqu’aucune pression ne s’y oppose, chaque atome tombe en chute libre vers le centre. On calcule alors le temps caractéristique de chute libre.
Le temps caractéristique de chute libre est l’ordre de grandeur pertinent du temps d’effondrement d’un nuage, en fonction des conditions. Il ne faudra pas y voir une valeur précise… On peut le définir comme le temps que met une particule de la périphérie à atteindre le centre.
On considère un objet, tel le nuage au début de son effondrement, mais le raisonnement pourra aussi bien s’adapter à un objet beaucoup plus compact, comme le cœur d’une étoile massive (à condition qu’il soit en chute libre). On suppose de plus que l’objet est de symétrie sphérique, et de masse M. La chute libre est l’effondrement gravifique de l’objet, lorsqu’aucune pression interne ne s’oppose au poids. C’est le cas lorsque l’objet est aussi dilué qu’un nuage pré-stellaire : les distances entre atomes sont telles, que toute énergie rayonnée (tout photon) passe librement entre eux et s’échappe, sans participer au chauffage et à la pression.
Considérons une particule de masse m, située à la surface de l’objet. Pour simplifier les calculs, nous allons admettre que toutes les particules plus proches du centre s’effondreront plus rapidement. Il en résulte que la masse située sous notre particule reste la même au cours de l’effondrement, et elle est égale à la masse totale M.
L’accélération subie par la particule est :
γ = - G M / R2
Nous allons prendre cette valeur comme constante pendant la partie de l’effondrement qui nous intéresse. Alors, pour se rapprocher du centre d’une distance Δr, la particule mettra un temps τ tel que :
γ τ2 / 2 = -Δr (- parce que le rayon diminue)
On définit le temps caractéristique de chute libre comme celui qui divise le rayon de l’objet par 2 : Δr = R / 2 . Donc :
-Δr = - R / 2 = γ τ2 / 2 = (- G M / R2 ) × τ2 / 2
d’où :
R = G M τ2 / R2
et : τ2 = R3 / G M
Le temps caractéristique est donc :
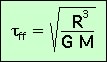
L’indice ff qui affecte τ signifie free fall (chute libre).
Nous retrouverons ce temps de chute libre plusieurs fois dans la vie d’une étoile. Il sera le temps caractéristique d’évolution à chaque fois que l’équilibre mécanique sera rompu, par défaut de pression centrale. Mais les conditions étant différentes, le temps pourra être très différent selon les étapes. Pour une étoile donnée, en supposant sa masse constante, le temps caractéristique de chute libre, d’après la formule, est fonction de R3/2. Lors de la contraction initiale de l’étoile, ce rayon sera de l’ordre de l’année-lumière, i.e. de 1013 km, alors que lors de l’effondrement du cœur d’une étoile massive, il ne sera que de l’ordre de 100.000 km. Le rapport de ces deux valeurs est de 1013 / 105 = 108 ; donc le temps caractéristique sera dans ce même rapport à la puissance 3/2, c’est-à-dire de l’ordre de 1012 = 1.000 milliards. Ce qu’il faut retenir, c’est que ce temps de chute libre est dans tous les cas très bref par rapport à la durée de la Séquence Principale.
Un nuage typique compte 1.000 atomes par cm3. Pour qu’il s’effondre, il doit atteindre au moins la masse de Jeans, c’est-à-dire 100.000 masses solaires. Pour appliquer la formule, il faut d’abord connaître le rayon du nuage.
Le nuage possède :
La masse volumique est donc la masse de ces 109 atomes d’hydrogène (dans un m3) : ρ = 109 × 1,672 10-27 kg m-3 = 1,672 10-18 kg m-3.
La masse est égale à la masse volumique multipliée par le volume :
M = ρ V = ρ 4/3 π R3 ⇒ R3 = 3 M / 4 π ρ
d’où : R3 = 3 × 2 1035 / 4 × 3,1416 × 1,672 10-18 = 0,29 1035+18 = 0,29 1053 m3 = 29 1051 m3
et : R = (29 1051)-3 m = 3,06 1017 m = 3,06 1014 km = 30,6 1013 km.
On sait qu’une année-lumière vaut 1013 km ; donc le rayon correspond à 30 AL soit à peu près 10 parsecs.
R = 10 pc
On peut maintenant calculer le temps de chute libre :
τff2 = R3 / GM = 0,29 1053 / (6,673 10-11 × 2 1035) = 0,0217 1053+11-35 = 0,0217 1029 = 21,7 1026
τff = (21,7 1026)1/2 = 4,66 1013 s
Une année compte 31 millions de secondes, donc :
τff = 4,66 1013 / 31 106 = 0,15 107 ans = 1.500.000 ans.
τff = 1.500.000 ans
En résumé, une partie d’un nuage, d’une dizaine de parsecs de diamètre et de quelques 100.000 masses solaires, peut s’effondrer sous une légère perturbation, en quelques millions d’années.
Cette partie est bien trop massive pour former une étoile. Le scénario précédent n’est donc que le début de l’histoire…
Une fois amorcé, l’effondrement se poursuit puisque la gravité l’emporte sur la pression. Il entraîne une augmentation de la masse volumique (même nombre d’atomes dans un volume plus restreint, ce qui revient à davantages d’atomes dans un même volume).
La masse de Jeans diminue, puisqu’elle varie comme l’inverse de ρ1/2. Par conséquent, lorsque ρ a suffisamment augmenté, des parties du nuage moins massives peuvent à leur tour s’effondrer : le nuage se fragmente.
Si on calcule le temps de chute libre du fragment, on trouve qu’il est plus petit que celui du nuage complet : dans la fragmentation, la contraction s’accélère.
Le scénario peut se répéter plusieurs fois, la masse volumique continuant d’augmenter, et la masse de Jeans de diminuer. La question est de savoir : jusqu’où ? Le nuage va-t-il se tranformer en un (très gros) tas de graviers ?
Pour répondre à cette question, il faut revoir les conditions que nous avons imposées pour montrer l’instabilité, et en déduire la masse de Jeans. La seule condition qui soit susceptible de changer est le caractère isotherme de l’effondrement !
Pourquoi le nuage est-il isotherme pendant la contraction ? Tout simplement parce que le temps de l’effondrement est beaucoup plus long que le temps de transfert de l’énergie. La chaleur produite au centre se propage à l’extérieur en une centaine d’années, alors que l’effondrement du nuage dure des millions d’années. Pendant l’effondrement, la température a dix mille fois le temps de s’uniformiser…
Cette uniformisation se perpétue-t-elle pendant toute la fragmentation ?
La réponse est : non !
A mesure que le nuage se fragmente, son opacité augmente. L’énergie s’en échappe de plus en plus difficilement : bientôt, il devient si opaque qu’elle ne peut plus se dégager. La contraction se fera alors sans échange d’énergie avec l’extérieur. D’isotherme (même température partout), la contraction devient adiabatique (sans échange d’énergie avec l’extérieur).
Le nuage devient opaque lorsque sa masse volumique atteint 10-13 g cm-3.
Le cœur est maintenant en équilibre hydrostatique, entouré d’un nuage toujours en chute libre. La masse du cœur est de l’ordre de 1031 g, soit 0,005 M. Son rayon est de l’ordre de 6 1011 m, sa masse volumique de 2 10-10 g cm -3 et sa température centrale de 170 K.
L’énergie s’accumule alors, et crée une pression qui s’oppose à la contraction.
Si on refait le calcul de la masse de Jeans, mais en supposant le nuage adiabatique (au lieu d’isotherme), on trouve qu’elle croît avec la masse volumique : plus le nuage se contracte, plus la masse de Jeans augmente. Le nuage ne peut donc plus se fragmenter.
On remarque ici que le nuage produit beaucoup d’énergie gravitationnelle, et qu’il commence à briller assez fortement. Mais sa température reste encore assez basse, et le rayonnement se fait majoritairement dans l’infra-rouge.
On peut calculer à quel moment (pour quelle masse), se produit la transition d’isotherme à adiabatique. Pour cela, on évalue l’énergie gravitationnelle produite par la contraction, et on prend la moyenne par unité de temps :
Eg = GM2 / R
Le temps de la contraction est le temps de chute libre : τff = (R3 / GM)1/2
Par unité de temps, le nuage rayonne donc le flux :
Fg = Eg / τff = GM2 / R × (R3 / GM)-1/2 = G3/2 M5/2 R-5/2
(le terme de droite, après le × est à la puissance -5/2 puisque le temps qu’il représente divise l’énergie).
D’autre part, le nuage rayonne dans l’espace. Si on suppose qu’il rayonne comme un corps noir, Fr = S σ T4, où S est la surface extérieure du nuage. Son rayon étant R, on a :
S = 4 π R2, Fr = 4 π R2 σ T4
L’objet rayonnant moins qu’un corps noir, on introduit un coefficient multiplicateur f plus petit que 1 :
Fr = f 4 π R2 σ T4 avec f < 1
Tant que l’énergie rayonnée reste supérieure à l’énergie gravitationnelle produite (Fr > Fg), le nuage ne peut se chauffer ; la contraction reste isotherme. Mais lorsque la contraction produit plus d’énergie que ce que le nuage peut rayonner (Fr < Fg), la température augmente. Le caractère isotherme est perdu, le nuage va vers le régime adiabatique. La transition entre les deux se fait à l’égalité :
Fr = Fg ⇒ f 4 π R2 σ T4 = G3/2 M5/2 R-5/2
La masse de Jeans la plus petite possible répond donc à cette équation ; c’est elle qu’il faut prendre ici. Donc Mj = M :
f 4 π R2 σ T4 = G3/2 M5/2 R-5/2
⇒ M5/2 = G-3/2 R5/2 (f 4 π R2 σ T4) = f 4 π σ T4 G-3/2 R9/2
Prenant la puissance -5/2 des deux membres et réarrangeant les termes, il vient :
M = (f 4 π σ)-5/2 G15/4 T-10 R45/4
Isolons f, dont la valeur n’est pas déterminée précisément ; c’est la masse de Jeans :
Mj = f -5/2 (4 π σ)-5/2 G15/4 T-10 R45/4
Dénommons k le terme constant (hors f), et calculons sa valeur :
k = (4 π σ)-2,5 G3,75 = [4 × 3,1416 × (5,670 10-8 W m2 K-4)]-2,5 × (6,674 10-11 m3 k-1 s-2)3,75
On obtient Mj = 1,62 10-23 f -5/2 T-10 R45/4, avec les unités ci-dessus.
Le calcul montre finalement que la masse de Jeans la plus petite possible est de l’ordre de la masse du Soleil !
Par conséquent, la fragmentation cesse pour des masses de l’ordre de celles des étoiles.
Cette théorie explique par conséquent comment un nuage, tels ceux que l’on observe dans les galaxies les plus proches, peut s’effondrer sous sa propre gravité, se fragmenter hiérarchiquement, pour produire des objets relativement denses de la masse d’une étoile.
Ces objets rayonnent un peu dans le visible, et beaucoup dans l’infra-rouge. On en observe dans les région HII de notre galaxie.
Cette théorie semble donc bien expliquer l’amorce de la formation des étoiles.
Soit un nuage de une masse solaire, qui en se fragmentant a multiplié sa densité (1.000 atomes par cm3 au départ) par 100.
La masse d’un proton est de 1,672 10-27kg, ou 1,672 10-24 g. Chaque cm3 du nuage a donc une masse 100.000 fois plus grande, donc la masse volumique en g par cm3 vaut 100.000 × 1,672 10-24 g cm-3= 1,672 10-19 g cm-3. Une masse solaire (2 1030 kg = 2 1033 g), occupera donc un volume :
V = 2 1033 g / 1,672 10-19 g cm-3 = 1,196 1052 cm3
V = 4π R3 /3 = 1,196 1052 cm3 ; on en déduit R3 = 3 × 1,196 1052 cm3 / (4 π) = 2,86 1051 cm3
Le rayon est la racine cubique de cette valeur :
R = 1,42 1017 cm = 1,42 1012 km, c’est-à-dire 1/10 d’année-lumière.
L’application de la formule donne :
τff2 = (1,4 1015 m)3 / (6,673 10-11 m3 kg-1 s-2 × 2 1030 kg) = 2,74 1045 / (13,346 1019) = 0,2 1045-19 = 0,2 1026 s2
Prenant la racine carrée, et divisant deux fois par 60, on obtient le temps en heures :
τff = 0,45 1013 s = 0,0074 1013 mn = 0,000125 1013 h = 1,25 109 h
Divisant encore par 24, puis par 365, on obtient le temps en années :
τff = 0,052 109 j = 0,00014 109 ans = 140.000 ans
τff =140.000 ans
---=OO=---