Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� L’Informatique en Astronomie | |||||||
L’ordinateur est un outil versatile, s’adaptant à toutes sortes de tâches différentes. C’est une machine à traiter l’information, et pour peu que l’on soit capable de la lui fournir sous la forme adaptée, elle peut la traiter à très grande vitesse, et de manière répétitive sans erreurs. L’informatique est utilisée un peu pour tout, et on ne s’étonnera pas donc de la voir en astronomie.
Le champ est d’ailleurs large. Nous allons examiner les différents secteurs où l’ordinateur est indispensable.
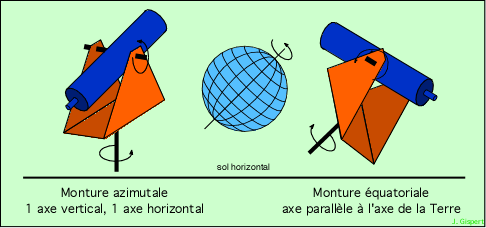
Pour suivre le mouvement apparent des astres dans le ciel, une solution mécanique simple consiste à faire tourner le télescope autour d’un axe parallèle à celui de la Terre, en sens inverse, et à la même vitesse. Alors, par un mouvement circulaire uniforme réalisable mécaniquement comme dans une horloge, on peut suivre très longtemps l’astre à observer.

Mais cette solution mécanique met le télescope en porte-à-faux, et limite le poids supportable par la fourche. Aussi a-t-elle été utilisée sur tous les instrument jusqu’à celui du Mont Palomar (miroir de 5 m de diamètre qui pèse à lui seul 15 tonnes). Ensuite, il a fallu abandonner cette solution mécanique simple, mais heureusement on a pu la remplacer par une solution informatique : l’axe principal de la monture est redressé à la verticale. Les mouvements sur les deux axes sont complexes, et dépendent de la hauteur de l’astre observé. Bref, il est impossible de réaliser une monture mécanique. Mais un ordinateur est tout à fait capable de calculer tous les mouvements à exécuter par les moteurs des axes, afin de piloter le tube du télescope exactement comme s’il était monté avec un axe parallèle à l’axe du monde. C’est la première révolution informatique en matière d’instrumentation, et elle est due aux soviétiques avec le télescope Bolchoï de Zélentchouk.

Le télescope E-ELT, montrant son miroir principal et sa structure image ESO
Les soviétiques ont pu ainsi contruire un télescope de 6 m de diamètre, mais ils se sont heurtés à une nouvelle limite : le poids du miroir. Pour assurer la rigidité du miroir, afin qu’il conserve sa forme parfaite dans toutes les positions d’observation, il fallait le réaliser dans un bloc de verre épais, et par conséquent lourd. Mais il y a pire. Lorsqu’on coule le miroir, le verre est à 1.000 degrés, et il doit refroidir. Si le refroidissement est rapide, il se forme d’abord une carapace dure de verre entourant un liquide. Ensuite ce liquide, en refroidissant se contracte, et il se crée des tensions dans le verre. Au moment de la taille du miroir, il casse. C’est arrivé aux soviétiques lors de la taille d’un premier miroir de 6 m.
Pour aller plus loin, il faut amincir le miroir, à la fois pour diminuer son poids et pour faciliter et accélérer le refroidissement. Mais on perd la rigidité. Pour palier à cet inconvénient, on place le miroir fini sur des vérins très précis, pilotés par ordinateur. 50 fois pas seconde, l’ordinateur analyse l’image d’une étoile donnée par le miroir, et de ses défauts déduit la forme du miroir. En agissant sur les vérins, il la corrige. Tous les télescopes modernes utilisent ce principe, nommé optique active.
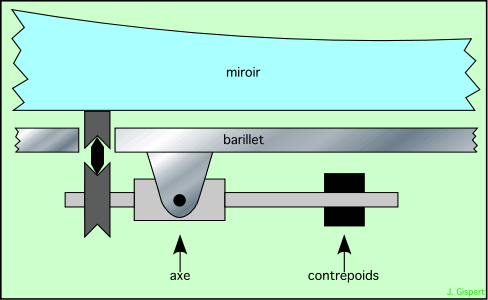
Les leviers astatiques utilisés autrefois sont remplacés par des vérins pilotés par l’ordinateur.
On construit des miroirs de plus en plus grand pour deux raisons :
Mais le second point ignore un problème important : avant de parvenir au miroir, la lumière des astres traverse l’atmosphère de la Terre. Or celle-ci est de mauvaise qualité optique. Ses différentes couches sont à des températures diverses, et l’indice de réfraction varie avec l’altitude. Mais en plus, il n’est pas stable, mais change constamment comme l’air surchauffé à la surface d’une route en été. Et la lumière des étoiles est déviée en permanence de façon totalement aléatoire par cette agitation. En pratique donc, le pouvoir séparateur réel (nommé seeing) d’un grand télescope ne dépasse pas celui d’un instrument d’amateur de 35 cm de diamètre !
Une solution à ce problème consiste à envoyer le télescope au-dessus de l’atmosphère, mais c’est très coûteux, et la réparation du télescope est bien difficile. Le HST est en orbite basse, et la navette spatiale était destinée en particulier aux réparations Mais ceci est terminé. Les navettes sont maintenant au musée.
L’autre solution, récente, consiste à analyser le problème. Le rayon lumineux qui nous parvient d’une étoile, est dévié par rapport à sa direction normale. Il suffit (sic) de produire une déviation en sens inverse pour l’annuler. Si le principe est simple, son application est démoniaque. La correction se fait par déformation d’un miroir, comme pour l’optique active. Mais l’analyse de l’image se fait après correction de la forme du miroir.

Diffusion Rayleigh au William Herschel Telescope (4,20 m) La Palma, Iles Canaries photo Olivier Martin
Par ce moyen, on arrive à récupérer au niveau du sol (dans les meilleurs sites mondiaux) une image aussi bonne que si le télescope était dans l’espace. C’est ainsi que les 4 VLT européens donnent des images bien plus fines que celles du télescope spatial américain.
L’interférométrie est une technique inaugurée par Edouard Stéphan à l’Observatoire de Marseille sur le télescope de Foucault. Si la lumière d’une étoile passe par deux trous à une distance d l’un de l’autre, les deux faisceaux émergeants produisent des franges d’interférence (expérience des fentes de Young). Mais une étoile présente un disque (inaccessible aux télescopes), et des rayons lumineux proviennent des différents points de ce disque. Par conséquent, en observant une étoile à travers deux trous, on produit plusieurs systèmes de franges d’interférence qui se superposent. Si le diamètre de l’étoile est petit, ces systèmes sont très proches les uns des autres, et leur superposition donne un système résultant bien net.
Par contre, si les bords de l’étoile sont éloignés (si son diamètre apparent est grand), les systèmes d’interférence sont décalés, et des franges lumineuses de l’un se superposent à des franges sombres d’un autre. Résultat : il y a de la lumière partout, et on n’observe pas de franges.
Mais la formation des franges dépend aussi de la distance entre les deux trous. En faisant varier cette dernière, pour une même étoile, on doit voir ou ne pas voir des franges. A la limite où les franges disparaissent, la distance d des deux trous permet de calculer le diamètre angulaire de l’étoile, puisque les systèmes de franges qui se recouvrent proviennent de deux bords opposés de l’étoile.
Le diamètre du télescope de Foucault étant de 80 cm, il n’était pas possible de faire varier la distance entre les trous. Stéphan a donc fixé celle-ci au maximum possible avec cet instrument. Et il a fait varier l’autre paramètre, le diamètre angulaire de l’étoile, en observant des étoiles différentes ! Il pouvait ainsi observer la disparition des franges pour toute étoile dont le diamètre angulaire aurait été supérieur à 0,158". Or il n’en a observé aucune… Cette première expérience n’a donc pas permi de mesurer le diamètre d’une étoile, mais montré que toutes celles qui avaient été observées étaient plus petites que 0,158". C’est le tout premier résultat concernant le diamètre des étoiles.
Les difficultés de mise en oeuvre de cette technique ont entraîné sa mise en sommeil. Seule une expérince du même genre a été faite une trentaine d’année plus tard sur le télescope de 2,50 m du Mont Wilson.
Plus tard, on a commencé à étudier les ondes radio émises par les astres (radioastronmie). Mais la longueur d’onde étant au moins 100.000 fois plus grande, la finesse des images est 100.000 fois plus mauvaise ! Pour obtenir une même finesse, les radioastronomes doivent utiliser des miroirs 100.000 fois plus grands (en diamètre) que ceux des astronomes optique…
Les plus grand radiotélescopes mobiles font 100 m de diamètre, ce qui est déjà énorme. Mais pas suffisant. Alors, les radioastronomes ont dû faire preuve de beaucoup d’imagination. Et ils ont trouvé une solution dans l’interférométrie. Mais contrairement à ce qu’on avait fait jusque-là, ils ont utilisé deux radiotélescopes, un pour chacun des faisceaux qui interfèrent. Et la finesse de l’image qu’on peut obtenir ainsi est définie par la distance entre les deux radiotélescopes.
Le problème est qu’il faut recontruire l’image par des calculs mathématiques extrêmement complexes. Seul l’ordinateur en est capable. Mais les résultats sont là.
Aujourd’hui, on connecte ainsi des radiotélescopes situés en des lieux très éloignés de la Terre, comme par exemple celui de Parkes en Australie avec celui de Jodrell Bank en Angleterre. On nomme cette technique VLBI pour Very Large Base Interferometrer. Et la finesse des images obtenues est meilleure que celle qu’on atteint en optique…
Sans doute est-il inutile de dire que les astronomes optique ont relevé le flambeau ? Mais disons-le tout de même. C’est Antoine Labeyrie sur le plateau de Calern près de Grasse, qui a réalisé le premier interféromètre optique. Les contraintes sont extrêmes, mais il a résolu les problèmes techniques.

Un télescope en béton de Labeyrie
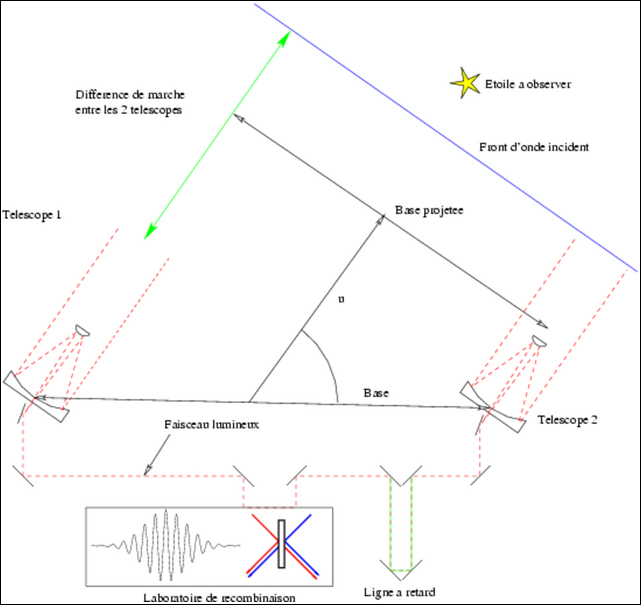
Principe de l’interférométrie à 2 télescopes
A la suite de ce travail, l’Europe s’est lancée dans la construction du VLT, Very Large Telescope. Il s’agit en fait de 4 télescopes identiques de 8,20 m de diamètre, groupés au sommet d’une montagne. On dispose ainsi de quatre instruments parmi les meilleurs du monde, pouvant mener quatre programmes de recherche simultanément; Cette réalisation se justifie pleinemet parce que le coût d’un télescope est fortement impacté par le coût des études et du développement. Construire quatre télescopes sur le même modèle coûte plus cher, mais pas beaucoup, et multiplie par quatre les résultats.
Le VLT a été conçu pour une utilisation en configuration VLTI (Very Large Telescope Interferometer). La lumière captée par ces télescopes est mélangée, pour produire des interférences (deux à deux). Et par des calculs de transformation de Fourier inverse, une image est recontruite.

Les 4 télescopes du VLT
Ces télescopes faisant 8,20 m de diamètre, soit 3,4 fois plus grands que le télescope spatial, permettent de reconstruire chacun une image 3 fois plus fine que celles données par le télescope spatial, grâce à l’optique adaptative. Mais en interféromètre, ils atteignent ensemble une finesse 80 meilleure que celle du télescope spatial.
C’est bien sûr grâce aux calculs très coûteux réalisés par l’ordinateur que cette performance est atteinte.
Nous avons vu certains domaines dans lesquels l’informatique s’est fait une place très importante. Mais elle s’est imiscée également dans de nombreux domaines où elle a fait ses preuves également, bien que leur apport soit moins visible.
Edouard Stéphan a réalisé cette expérience à Marseille sur le télescope de Foucault, en plaçant à son ouverture un cache percé de deux trous. Il n’a pu observer la disparition des franges, parce que le télescope est trop petit. Mais il a montré que le diamètre de toutes les étoiles observées est inférieur à 0,158", donnant ainsi pour la première fois une idée du diamètre apparent des étoiles.
Depuis cette expérience historique, Antoine Labeyrie, sur le plateau de Calern, a développé une technique très délicate d’interférométrie à deux télescopes. L’utilisation de deux instruments a pour avantage de ne plus limiter la précision, les télescopes pouvant théoriquement être aussi éloignés qu’on le désire.
Le VLT a été conçu en particulier pour fonctionner en VLT-I (Very Large Telescope Interferometer). La reconstitution d’une image à partir des données interférométriques est un calcul très très complexe. Mais possible. Et le pouvoir séparateur de l’instrument résultant est donné par la distance entre les télescopes.
La mécanique céleste est le domaine le plus naturel d’application de l’informatique, par l’abondance des calculs qu’elle nécessite. La loi de la Gravitation Universelle permet de définir le mouvement des astres, mais les équations sont très complexes. Pour calculer par exemple les éclipses des satellites du Jupiter, il faut résoudre pas à pas, à des intervalles de temps de l’ordre de l’heure, un ensemble d’équations différentielles. Des techniques mathématiques (différences finies) permettent de mettre le problème en forme. Ensuite, des ordinateurs puissants permettent d’effectuer les masses de calcul nécessaires pour construire des tables de position.
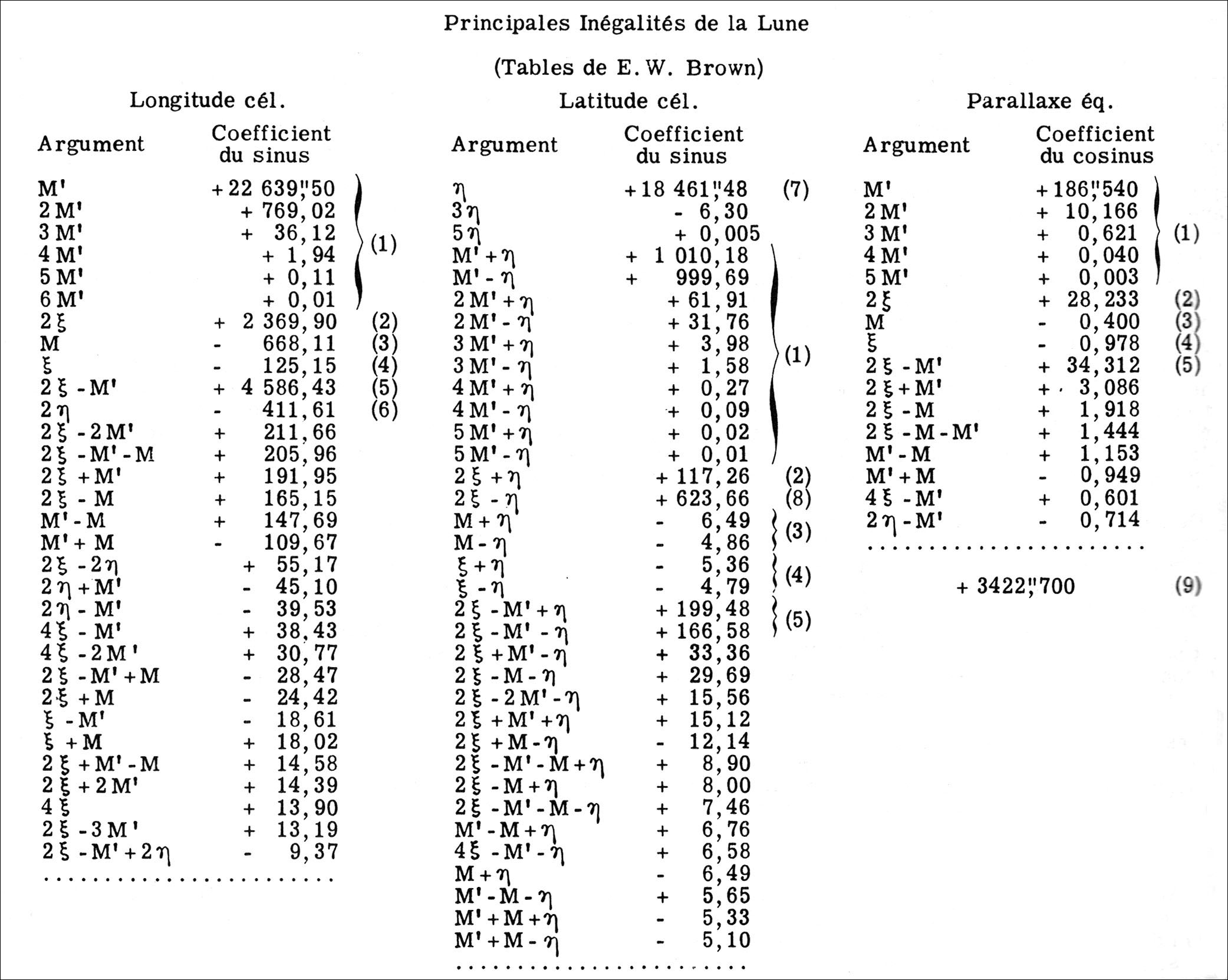
Un aperçu de la complexité…
On remarquera que la théorie des satellites de Jupiter a permi la première mesure de la vitesse de la lumière ! L’erreur périodique constatée entre les positions calculées et les positions observées a été interprétée par Römer comme due à la différence de distance entre la Terre et Jupiter au cours de l’année. Elle a donné un excellent ordre de grandeur de cette vitesse.
L’astronomie s’est développée considérablement depuis l’apparition des fusées. Les meilleures photos que l’on peut faire aujourd’hui depuis le sol ne nous permettraient toujours pas de comprendre la physique des planètes géantes, ou la géologie de Mars…
Mars donc ne se présente que comme un minuscule disque sur lequel on distingue des taches plus ou moins colorées (figures d’albédo).

Opposition 27/08/03 photo S. Lisciandra
Difficile, dans de telles conditions, de faire de la bonne science !

Myrtille (sphérule d’hématite) vue sur place par Opportunity…
On a posé une sonde sur le sol de Titan, satellite de Saturne, à 1,4 milliards de km de chez nous ! Pour réussir un tel exploit, il faut maîtriser la mécanique céleste. Celle-ci utilise la même loi de la Gravitation Universelle que le calcul des éphémérides, mais les problèmes sont un peu différents. En tous cas, les résultats sont là.

Le robot scientifique Curiosity
L’exploration robotisée des planètes est infiniment plus simple que l’exploration humaine. Un robot possède un billet aller-simple ! Il n’a pas besoin de nourriture, pas besoin d’oxygène, il résiste très bien au froid…
Les robots Rocky, Spirit, Opportunity, Curiosity, pratiquent une exploration systématique de la surface de Mars, avec des moyens d’analyse très performants. Les résultats qu’ils apportent sont considérables, et impossible à obtenir à distance.
La distance minimale entre la Terre et Mars est de 60 millions de km. La lumière met 3 minutes 20 secondes pour franchir cette distance. Au plus loin, le temps est de 21 minutes. Le pilotage d’un robot depuis la Terre nécessiterait 2 fois ce temps pour amener une vue du paysage sur Terre, l’analyser et envoyer une commande vers Mars. Même à la vitesse d’un escargot, le robot aurait bien le temps de tomber dans un précipice avant que l’ordre d’arrêt lui parvienne !
Le robot doit donc être totalement autonome, et capable de circuler sur un terrain accidenté, où personne n’a tracé de routes…
Les étoiles sont d’énormes boules de gaz en équilibre entre leur propre poids, qui tend à les écraser, et la production d’énergie en leur centre, qui tend à les faire éclater. L’énergie est produite par des réactions thermonucléaires de fusion de l’hydrogène (pendant la plus grande partie de la vie de l’étoile), ou de l’hélium… Ces réactions sont plus ou moins rapides selon la température. Et une augmentation de température produit une dilatation, et par suite un refroidissement, ce qui ralenti les réactions. Cette boucle permet à l’étoile de maintenir un équilibre très précis sur des durées très grandes. L’évolution du taux de réaction répond à un système d’équations différentielles. Seul un calcul par ordinateur est capable de nous indiquer comment une étoile va évoluer.
On cosntruit un modèle, qui est un ensemble d’équations différentielles. Ensuite on transforme ces équations en équations aux différences finies, puis on écrit un programme pour les calculer. Plus grande est la précision recherchée, plus les calculs sont importants. De plus, les résultats concernent seulement le jeu de paramètres utilisés. Pour d’autres valeurs de ces paramètres, il faut refaire des calculs.
Ensuite, l’analyse des résultats numériques peut parfois mettre sur la piste d’une loi qui représenterait empiriquement le modèle. Les simulations numérique peuvent donc, dans un domaine où elles sont impossibles, remplacer les expérimentations.
Une galaxie est un ensemble de plusieurs dizaines, voire plusieurs centaines de milliards d’étoiles. Elles tournent toutes autour du centre de la galaxie, mais leur densité diminue en allant du centre vers l’extérieur. Aussi, la détermination de la masse qui attire une étoile particulière n’est pas évidente. Là encore, on écrit des modèles qui représentent la structure de la galaxie, et calcule l’évolution. Un des problèmes essentiels est la stabilité des galaxies.
Un autre problème, longtemps non résolu, concerne des galaxies dites "anormales". Par exemple les antennes de Arp.
Mais on a tenté de simuler des collisions de galaxies. Pour commencer, on a représenté une galaxie par un ensemble d’un millier d’étoiles. Ceci n’était absolument pas réaliste, mais a permi de valider la méthode. Ensuite, avec les progrès à la fois des ordinateurs (groupes d’ordinateurs) et de la programmation, on est arrivé à simuler des galaxies de plusieurs millions d’étoiles. Ce qui commence à être assez représentatif. Et les résultats ont été surprenants. Un objet anormal comme les antennes a été reproduit comme conséquence de la collision de deux galaxies spirales !

La galaxie des Antennes de Arp
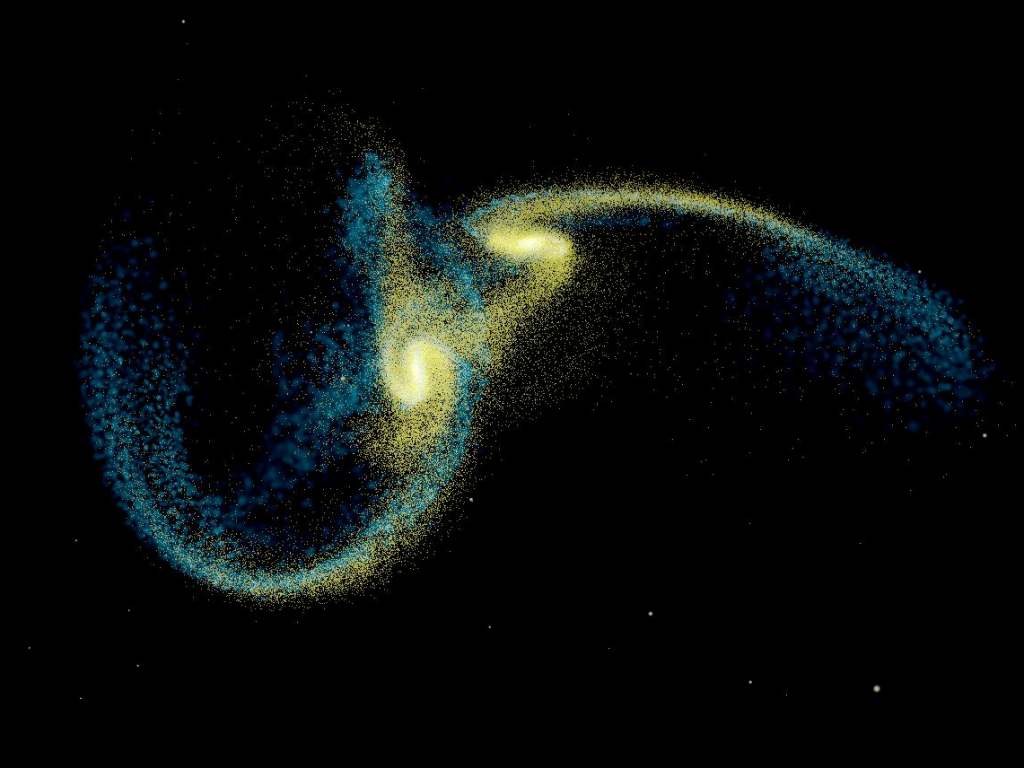
Collision de deux galaxies spirales, simulation
---=OO=---