Historique de Marseille
| liens |
le 18/08/17
| Bonne année 2026 ! |
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
|||||
| �� Assistance Gravitationnelle |
| |||||||
Dans un précédent séminaire, nous avons considéré le voyage d’une sonde d’une planète à une autre, dans sa phase interplanétaire seule. La solution la plus économique est le transfert de Hohmann. Nous allons maintenant envisager les phénomènes qui peuvent se produire lorsque la sonde atteint la planète cible.
Revenons d’abord sur ce transfert. On considère deux planètes dont les orbites sont supposées circulaires pour simplifier. L’orbite de transfert est une ellipse (dont la sonde parcoura la moitié) tangente aux deux orbites. Soient R et r les rayons des deux orbites planétaires (les lettres R et r sont mises pour rayons, puisque les orbites sont considérées circulaires ; on suppose R > r). Les éléments de l’orbite de Hohman sont :
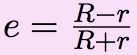
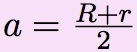
Quelle est la vitesse de la sonde à l’approche de la cible ? Son orbite est un arc d’ellipse autour du Soleil. Le carré de la vitesse d’un objet (sonde ou planète) sur une orbite elliptique est, lorsqu’il est à la distance ρ du Soleil :
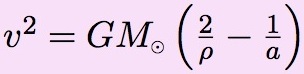
a étant le demi grand-axe de l’orbite de transfert, ρ la distance de la sonde au Soleil, G la constante de la gravitation universelle, et enfin M la masse du Soleil.
Si la planète visée est une planète supérieure (Mars par exemple), le départ se fait du périhélie, et l’arrivée à l’aphélie. Donc, pour l’orbite de transfert, le périhélie q = r = rayon de l’orbite terrestre, et l’aphélie Q = R = rayon de l’orbite de Mars. Pour une planète inférieure, le rôle de la Terre est inversé : q = r = rayon de l’orbite de Vénus, et Q = R = rayon de l’orbite terrestre, en prenant toujours la lettre minuscule pour l’orbite la plus petite.
Dans la suite, nous allons considérer une sonde partant de la Terre, à destination de Mercure, en passant par Vénus. Nous verrons quel est l’avantage de cet intermédiaire. Ce voyage sera composé de deux arcs d’orbite : le premier est un transfert de Hohmann entre la Terre et Vénus, et le second un autre transfert de Hohmann entre Vénus et Mercure. On sait que chacun est optimal (en termes d’énergie) ; la question sera de savoir si leur composition l’est aussi…
Pour une raison qui apparaîtra plus loin, nous allons commencer par déterminer la formule qui donne la vitesse orbitale d’une planète, en supposant son orbite circulaire.
vp2 = G M (2/ρ - 1/a), où ρ = r, et a = r (r rayon de l’orbite de la planète, l’orbite étant supposée circulaire, ρ est constant égal au rayon de l’orbite).
Donc vp2 = G M (2 / r - 1 / r) = G M / r.
| (1) | 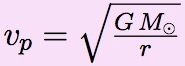 |
La vitesse de la planète est indicée avec un 'p' minuscule ; le rayon est noté 'r' minuscule. Pour une planète supérieure, on remplacera ces deux minuscules par des majuscules, ce qui ne change que la notation, et non la signification de la formule.
On remarque que cette vitesse varie inversement proportionnellement à la racine carrée du rayon r. Or la racine carrée augmente très vite quand on part de 0, puis de plus en plus lentement. Quand on arrive à de grandes valeurs de r, une petite variation de r en plus ou en moins ne change pas grand chose (les matheux calculent la dérivée pour s’en assurer, et constatent qu’elle tend vers 0 quand r tend vers l’infini). Et en effet, plus les planètes sont loin du Soleil, plus leurs vitesses sont semblables :
Alors qu’entre Mercure et Vénus la différence de vitesse est de 12,85 km s-1 pour une différence de distance au Soleil de seulement 50,3 millions de km,
entre Uranus et Neptune la différence de vitesse est de 1,44 km s-1 pour une différence de distance au Soleil de 1,63 MILLIARDS de km.
Cette remarque nous servira plus loin pour comprendre le coût des transferts.
Considérons le transfert de Hohmann vers une planète inférieure. On doit déterminer les vitesses de la sonde au départ et à l’arrivée. Entre ces deux positions, elle est en mouvement inertiel sur l’orbite.
Il y a deux planètes à considérer. Pour avoir une notation simple, on désignera par p la plus proche du Soleil, et par P la plus éloignée. C’est la même convention que pour les rayons.
Le demi grand-axe de l’orbite est a = (R + r) / 2. Au départ, la sonde est en ρ = R (elle part de la planète la plus loin du Soleil). L’application de la formule donne :
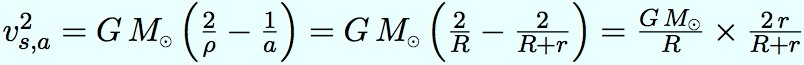
vs,a représente la vitesse de la sonde (s) à l’aphélie (a).
Le premier terme de droite, G M / R, est le carré de la vitesse de la planète de départ. On notera cette vitesse vP, avec un P majuscule en indice.
| (2) | 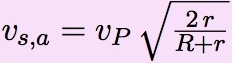 |
vs,a est la vitesse de la sonde à l’aphélie de l’orbite de Hohmann.
On fait le même calcul pour la vitesse d’arrivée de la sonde, au périhélie de l’orbite de transfert. Le demi grand-axe de l’orbite est évidemment le même, mais maintenant la sonde est près de la planète inférieure, donc ρ = r.
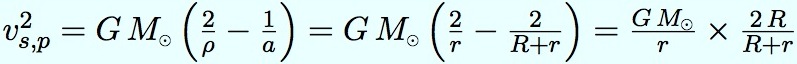
Le premier terme à droite représente la vitesse de la planète cible sur son orbite (puisqu’il y a r au dénominateur). On notera cette vitesse vp, avec un p minuscule en indice. Donc :
| (3) | 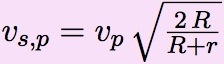 |
Cas d’une planète supérieure : considérons deux planètes nommées A et B, A étant plus près du Soleil que B. A est une planète inférieure pour B, et B est une planète supérieure pour A. Ces rôles sont parfaitement symétriques.
Ces deux demi-ellipses sont les deux moitiés de la même ellipse, la seule tangente aux deux orbites.
Il s’ensuit que la vitesse d’une sonde près d’une planète est la même qu’elle en parte ou qu’elle y arrive, puisque les vitesses de part et d’autre du périhélie sont symétrique (idem à l’aphélie). Si la planète est la plus loin du Soleil, c’est la vitesse aphélique de la sonde ; sinon c’est sa vitesse périhélique.
Les formules à utiliser sont donc :
| cible inférieure | cible supérieure | |
|---|---|---|
| départ | 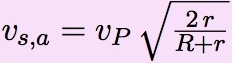 | 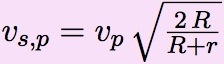 |
| arrivée | 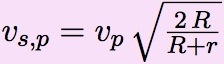 | 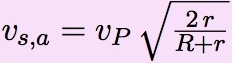 |
Il y a beaucoup de similitudes entre les deux formules :
- la vitesse de la planète qui y figure est celle de la planète où se trouve la sonde.
- cette vitesse est multipliée par la racine carrée d’un rapport, dont seul le numérateur diffère. Il contient le rayon de l’orbite à atteindre, l’orbite de l’autre planète.
Les formules (2) et (3) que nous venons d’établir sont suffisantes pour calculer les transferts de Hohmann. Nous les appliquerons pour définir le trajet interplanétaire.
Quelles sont les manœuvres à faire pour que la sonde atteigne sa cible ?
Au départ, elle est lancée depuis le sol, puis placée sur une orbite solaire quasiment identique à l’orbite de la planète d’où elle part (pour l’instant la Terre, mais une autre planète si on en ramène des échantillons). Donc, la sonde accompagne la planète, et va à la même vitesse qu’elle.
A l’arrivée, la sonde doit se placer sur une orbite solaire identique à celle de sa cible, donc à la même vitesse. Ensuite, elle pourra s’y poser éventuellement, mais ce n’est pas ce qui nous occupe maintenant.
Dans les deux cas, la vitesse de la sonde doit changer, et il faut une manœuvre pour lui donner la bonne vitesse.
Pour atteindre sa cible, elle doit modifier sa vitesse selon l’une des formules que nous venons d’établir. C’est cette variation de vitesse qui constitue la manœuvre de départ. Si la vitesse de la sonde doit être supérieure à la vitesse de la planète, il lui faudra accélérer, sinon elle devra freiner.
| la sonde va de la planète supérieure à la planète inférieure elle se rapproche du Soleil | la sonde va de la planète inférieure à la planète supérieure elle s’éloigne du Soleil | |||
| Départ | vitesse initiale de la sonde = vitesse de la planète supérieure | vitesse de départ de la sonde = vitesse de l’aphélie de Hohmann | vitesse initiale de la sonde = vitesse de la planète inférieure | vitesse de départ de la sonde = vitesse du périhélie de Hohmann |
|---|---|---|---|---|
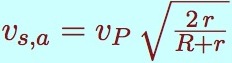 | 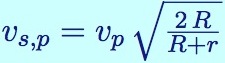 | |||
| Arrivée | vitesse d’arrivée de la sonde = celle du périhélie de Hohmann | vitesse finale de la sonde = celle de la planète inférieure | vitesse d’arrivée de la sonde = celle de l’aphélie de Hohmann | vitesse finale de la sonde = celle de la planète supérieure |
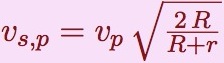 | 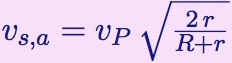 | |||
Voyage vers une planète inférieure. C’est la partie gauche du tableau qui concerne ce cas.
Voyage vers une planète supérieure. C’est la partie droite du tableau qui concerne ce cas.
Pour résumer cela :
Dans ce qui suit, nous prendrons comme exemples la Terre, Vénus et Mercure. Le tableau ci-dessous en donne les éléments nécessaires, à l’approximation des orbites circulaires.
| Terre | Vénus | Mercure | |
|---|---|---|---|
| Vitesse orbitale | 29,79 km s-1 | 35,02 km s-1 | 47,87 km s-1 |
| Rayon de l’orbite | 149,6 106 km | 108,2 106 km | 57,9 106 km |
Pour un voyage Terre-Mercure, les paramètres sont : r = 57,9 106 km ; R = 149,6 106 km.
| départ de la Terre formules en haut à gauche du tableau | vitesse de la planète (la Terre) | vitesse de la sonde (aphélie) | freinage |
| 29,79 km s-1 | 22,25 km s-1 | 7,54 km s-1 | |
| arrivée sur Mercure formules en bas à gauche du tableau | vitesse de la sonde (périhélie) | vitesse de la planète (Mercure) | freinage |
| 57,48 km s-1 | 47,87 km s-1 | 9,61 kms-1 |
La vitesse de la sonde à l’aphélie se calcule par :
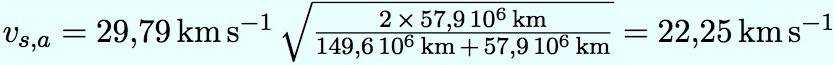
Le freinage est la différence entre la vitesse avant le départ (celle de la planète), et la vitesse de descente (celle de l’aphélie).
A l’arrivée, on utilise la formule donnée en bas à gauche du tableau, soit vs,p

Le transfert de Hohman direct Terre-Mercure coûte donc (uniquement dans sa partie interplanétaire) :
Le transfert se fait par l’orbite de Hohmann décrite par :
a = (R + r) / 2 = 103,75 106 km.
e = (R - r) / (R + r) = 91,7 / 207,5 = 0,442.
On détermine le coût de chacun des arcs de Hohmann (Terre-Vénus et Vénus-Mercure).
Trajet Terre-Vénus : la Terre est le point de départ, et Vénus celui d’arrivée. R sera encore le rayon de l’orbite de la Terre, et r celui de Vénus (l’aphélie de l’orbite de transfert est au niveau de la Terre, le périhélie au niveau de Vénus). Le calcul est identique au précédent, avec les mêmes formules :
| départ de la Terre formules en haut à gauche du tableau | vitesse de la planète (la Terre) | vitesse de la sonde (aphélie) | freinage |
| 29,79 km s-1 | 27,29 km s-1 | 2,50 km s-1 | |
| arrivée sur Vénus formules en bas à gauche du tableau | vitesse de la sonde (périhélie) | vitesse de la planète (Vénus) | freinage |
| 37,73 km s-1 | 35,02 km s-1 | 2,71 kms-1 |
Encore un calcul complet, celui de l’aphélie :

Le reste se calcule exactement comme pour le cas du voyage Terre-Mercure. La vérification vous est laissée…
coût total Terre-Vénus : 2,50 km s-1 + 2,71 km s-1 = 5,21 km s-1
Trajet Vénus-Mercure : R = 108,2 106 km, rayon de l’orbite de Vénus, r = 57,91 106 km, rayon de l’orbite de Mercure.
| départ de Vénus formules en haut à gauche du tableau | vitesse de la planète (Vénus) | vitesse de la sonde (aphélie) | freinage |
| 35,02 km s-1 | 29,24 km s-1 | 5,78 km s-1 | |
| arrivée sur Mercure formules en bas à gauche du tableau | vitesse de la sonde (périhélie) | vitesse de la planète (Mercure) | freinage |
| 54,64 km s-1 | 47,87 km s-1 | 6,77 kms-1 |
coût total Vénus-Mercure : 5,78 km s-1 + 6,77 km s-1 = 12,55 km s-1
En comparant les coûts des transferts Terre-Vénus et Vénus-Mercure, on voit que le second est beaucoup plus coûteux. Pourtant, la distance entre les orbites de la Terre et de Vénus, et la distance entre celles de Vénus et de Mercure sont du même ordre de grandeur. Le coût plus élevé entre Vénus et Mercure se justifie par la plus grande proximité du Soleil, qui exerce une attraction plus forte. La remarque concernant la formule (1) explique que la vitesse orbitale croît très vite lorsqu’on s’approche près du Soleil. Pour deux planètes écartées de 50 millions de kilomètres, la différence de vitesse sera bien plus grande si elles sont proches du Soleil que loin. La vitesse d’une sonde allant de l’une à l’autre sera du même ordre de grandeur que les vitesses orbitales. On comprend donc bien que les vitesses de la sonde à l’aphélie et au périhélie soient d’autant plus différentes que les planètes sont plus proches du Soleil. Le surcoût s’en déduit directement.
On peut regrouper les termes de freinage au niveau de Vénus. Le premier (2,71 km s-1) est le freinage à l’arrivée de la Terre, le second (5,78 km s-1) le freinage au départ vers Mercure. Mais dans ce calcul, on n’a pas pris en compte la présence de Vénus, et tout se passe comme si la planète n’était pas là ; on la considérera plus bas. On peut donc tout à fait regrouper ces deux termes, qui représentent le freinage total à effectuer au niveau de l’orbite Vénusienne, soit 2,71 km s-1 + 5,78 km s-1 = 8,49 km s-1. C’est cette valeur que l’on envisagera de prélever à la planète pour économiser le carburant.
Le rapport de masse est le nombre par lequel il faut multiplier le poids de la charge utile pour trouver le poids du lanceur nécessaire. Un bon rapport de masse est de l’ordre de 30 (pour une satellisation en orbite basse). Vu de l’autre côté, la charge utile ne représente que 3 % de la masse de la fusée sur le pas de tir (dans les bons cas, toujours pour l’orbite basse).
Analogie pour comprendre le rapport de masse : envisageons de faire le tour du monde en voiture, sans jamais s’arrêter à une station-service ! Mettons que notre voiture consomme 5 l/100 km. Pour effectuer les 40.000 km de la circonférence de la Terre, il faut 5 l x 40.000 km / 100 km = 2.000 l de carburant, soit 1.500 kg de carburant, occupant un réservoir de 2 m3. Ces nombres ne sont pas vraiment impressionants, mais il sera tout de même difficile de trouver une voiture avec un tel réservoir. Il faudra alors se rabattre sur un petit camion citerne. Mais sa consommation est plutôt de 30 l / 100 km, et il devra emporter 12.000 l de carburant…
Le voyage Terre-Mercure direct coûte, pour sa partie interplanétaire, 17,15 km s-1. En passant par Vénus, il en coûte 17,76 km s-1. Soit légèrement plus. On aurait pu s’attendre à ce que le coût soit plus élevé, mais l’ordre de grandeur est le même. Si on n’utilise pas l’assistance de Vénus, le voyage direct est préférable.
Sans l’assistance de Vénus (voyage direct), il faudrait freiner de 9,61 km s-1 au niveau de Mercure, et pour cela amener sur place un moteur, des réservoirs et du carburant (beaucoup). Tout ceci aurait dû être placé en orbite terrestre, puis subir le freinage au départ de la Terre. Un coût très élevé. C’est ce que nous voulons économiser. Avec les moyens de lancement actuels, la charge utile serait nulle dans ces conditions…
Comment faire cette économie n’est pas facile à concevoir. Mais une fois la solution trouvée, il suffira de piloter la sonde pour qu’elle passe à la bonne distance de la planète, afin d’en recevoir juste l’impulsion nécessaire.
| comparaison des vitesses | |||
|---|---|---|---|
| départ Terre | arrivée Vénus | départ Vénus | arrivée Mercure |
| 27,29 km s-1 | 37,73 km s-1 | 29,24 k s-1 | 54,64 km s-1 |
| vitesse Terre | vitesse Vénus | vitesse Mercure | |
| 29,79 km s-1 | 35,02 km s-1 | 47,87 km s-1 | |
| freinage départ | freinage au niveau de Vénus | freinage à l’arrivée | |
| 2,50 km s-1 | 8,49 km s-1 | 6,77 km s-1 | |
Sur ce tableau, on vérifie bien ce qui a été dit plus haut sur une base théorique.
Dans le séminaire précédent, nous avons vu la formule qui donne la période orbitale :
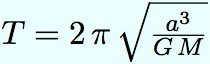
Puisque le trajet de Hohmann est une demi-ellipse, la durée de son parcours est la moitié de la période de l’orbite. On peut donc calculer facilement les durées de trajet de la Terre à Mercure, soit directement, soit en passant pas Vénus.
| Terre-Mercure direct | Terre-Vénus | Vénus-Mercure | Terre-Mercure par Vénus | |
|---|---|---|---|---|
| durée du trajet | 105,47 jours | 146,06 jours | 75,54 jours | 221,59 jours |
On remarque tout de suite que le voyage vers Mercure, en passant par Vénus, est plus de deux fois plus long que le voyage direct. Et il coûte un peu plus d’énergie sans assistance gravitationnelle…
Mais tout de même, le voyage est très rapide. 210 jours ne représentent que 7 mois de voyage. Donc, si on envoyait une sonde vers Vénus en utilisant le carburant nécessaire pour l’injecter sur le trajet de Hohmann adhoc, en assurant le freinage au niveau de Vénus par assistance gravitationnelle, il resterait encore beaucoup d’énergie à mettre au niveau de Mercure pour freiner. Un tel voyage, rapide, est encore bien trop coûteux.
Supposons tout d’abord un astre (planète, étoile, peu importe), isolé dans l’univers, et une sonde qui passe à proximité. Elle n’est soumise qu’à la gravité de l’astre. Nous savons bien que le problème a trois volets :
Cette remarque amène deux conséquences :
La première de ces régions est une sphère centrée sur Vénus, et dans laquelle on considérera que la sonde n’est soumise qu’à l’attraction de la planète, en négligeant celle du Soleil. On la nomme sphère d’influence.
La seconde région est l’univers, moins la sphère d’influence. Cette région contient le Soleil. On se limitera tout de même à la sphère d’influence du Soleil (qui contient le système solaire).
La sphère d’influence s’étend autour de la planète jusqu’à une distance où l’attraction du Soleil est supérieure à celle de la planète. Mais c’est un phénomène dynamique. On ne peut pas déterminer le rayon de cette sphère sans tenir compte du mouvement de la planète autour du Soleil.
Nous ne démontrerons pas la formule qui donne son rayon ; la voici :
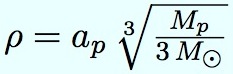
Où ap est le demi grand axe de l’orbite de la planète, Mp sa masse, et M celle du Soleil.
On remarque que :
Remarque : si on considère une planète isolée dans l’espace, ceci revient à envisager que le Soleil est rejeté à l’infini. Dans ces conditions, la sphère d’influence de la planète s’étend à l’infini, ce qui correspond bien à ce qu’on attend.
Sur son orbite de transfert, la sonde est soumise à l’attraction du Soleil, et on néglige celle de Vénus. Puis elle approche de la planète, et brutalement, on considère qu’elle est soumise à Vénus et plus au Soleil. Dans la réalité, la transition est progressive, une influence augmentant jusqu’à dépasser l’autre. Mais jamais elles ne s’annulent. Cependant, cette approximation a l’avantage de distinguer deux régions dans lesquelles les problèmes sont simples, et de montrer comment les choses se passent, au moins qualitativement.
Cette analyse montre qu’on peut approcher de Vénus selon la trajectoire de Hohmann, qui néglige l’attraction de la planète. Les modifications à envisager seront donc uniquement à proximité de Vénus.
En admettant que Vénus soit seule dans l’Univers, avec la sonde, celle-ci pénétrerait dans la sphère d’influence de la planète selon une trajectoire hyperbolique, avec une certaine vitesse, et en ressortirait avec la même vitesse (sous un angle différent). Mais il faut considérer que Vénus n’est pas isolée, et qu’elle tourne autour du Soleil. Son orbite est balistique, puisqu’elle ne reçoit par d’énergie pour la maintenir. C’est un mouvement inertiel, dont l’impulsion est proportionnelle à la masse de la planète. Pareillement, la sonde effectue un vol balisitique, inertiel, dont l’impulsion est proportionnelle à sa propre masse. L’idée est maintenant toute simple : on s’approche de Vénus, qui va produire un lien gravitationnel avec la sonde. Elles vont exercer l’une sur l’autre une force d’attraction identique, mais évidemment la sonde va être entraînée infiniment plus que la planète, en fonction de leurs masses respectives. C’est ainsi que la sonde vole un peu d’énergie à la planète, qui ne s’en porte pas plus mal…
C’est donc bien un peu de l’énergie cinétique de Vénus que la sonde doit emprunter. Et c’est cette énergie qui doit accélérer ou freiner la sonde, selon les nécessités. La modification de direction qui en est le corolaire n’est pas forcément souhaitable, mais en calculant bien les trajectoires, on peut en faire un apport positif.
Lorsque la sonde arrive dans la sphère d’influence de la planète, une interaction gravitationnelle se produit entre elles. Nous allons analyser l’essentiel de cette interaction.
On considère le système planète-sonde comme isolé dans l’espace, sans interactions avec le reste de l’univers. Alors, ce système possède une certaine quantité de mouvement. La quantité de mouvement, qu’on appelle plutôt impulsion aujourd’hui, est le produit de la masse de l’objet par sa vitesse. En parlant de vitesse, on signifie le vecteur vitesse, car la direction a bien évidemment une grande importance. Et par suite, l’impulsion est aussi un vecteur, qui a une direction, la même que la vitesse :
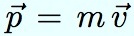
Puisque nous considérons que le système est isolé, il n’échange pas d’énergie avec l’extérieur (ce qui est vrai avec une bonne approximation), et par conséquent sa quantité de mouvement TOTALE reste constante. La quantité de mouvement des deux objets est la somme de leurs quantités de mouvement, soit : 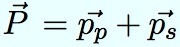 , où
, où ![]() est la quantité de mouvement de la planète, et
est la quantité de mouvement de la planète, et ![]() celle de la sonde.
celle de la sonde.
Cette somme reste constante, alors que les deux termes peuvent varier. Donc, on peut envisager :
De combien varient les vitesses de la sonde et de la planète ? Calculons la variation de l’impulsion du système planète-sonde :
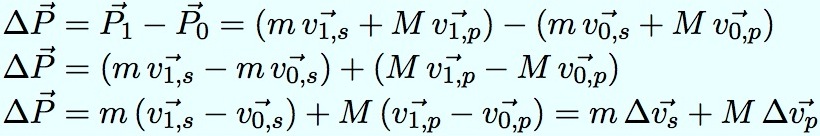
Ce que perd la planète, la sonde le gagne.
Nous avons maintenant la formule qui donne la variation de l’impulsion du système planète-sonde. En considérant que ce système n’a pas d’interactions avec l’extérieur (il est isolé), son impulsion est constante, et sa variation est par conséquent nulle. Donc :
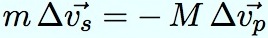
Cette relation montre que, les masses de la sonde et de la planète étant considérées comme constantes à une excellente approximation, la variation de vitesse de la sonde par rapport à celle de la planète est de :
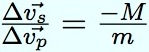
La variation de vitesse est inversement proportionnelle à la masse des objets. Il est évident que la masse de la planète est extrêmement plus élevée que celle de la sonde. Donc une variation significative de la vitesse de la sonde se traduira par une variation infinitésimale de celle de la planète.
Dans la sphère d’influence, la sonde peut approcher la planète de deux côtés. Soit devant, soit derrière, par rapport à son mouvement orbital. Voyons les deux cas :
Accélération veut dire augmentation de la vitesse, ET changement de direction. Idem pour le ralentissement.
Si la planète est devant la sonde, elle l’entraîne. Elle lui cède une petite fraction de son énergie cinétique.
formule de Rutherford : D = 2 arctan(GM/v02d) d paramètre d’impactLe calcul de la sphère d’influence de Vénus (voir la formule plus haut) donne :
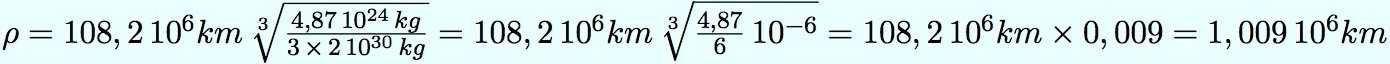
La sphère d’influence autour de Vénus s’étend donc jusqu’à 1 million de km (frontière où l’influence du Soleil se fait bien sentir, mais est minoritaire). La sonde doit donc passer à l’intérieur de cette sphère pour subir la gravité de Vénus, et voir sa trajectoire modifiée de manière significative.
Le prochain paramètre à considérer est la vitesse de la sonde dans cette sphère d’influence. Si elle est trop faible, la sonde sera capturée par la planète, ce qui n’est pas le but. Donc, elle doit garder une vitesse supérieure à la vitesse de libération. Mais attention, que signifie vitesse de libération ? C’est la vitesse que l’on doit donner à un mobile pour qu’il échappe à la planète, depuis le sol. Mais la sonde ne partira pas du sol… Il faut donc évaluer la vitesse de libération en fonction de l’altitude à laquelle elle va passer au plus près de la planète.
La vitesse de la sonde n’est pas prise par rapport au Soleil, mais par rapport à la planète elle-même. Donc, c’est la différence entre la vitesse de la sonde et celle de Vénus : V = 37,73 km s-1 - 35,02 km s-1 = 2,71 km s-1. A quelle altitude au-dessus de Vénus cette vitesse est-elle la vitesse de libération ? Pour le savoir, il suffit de prendre la formule qui donne la vitesse de libération en fonction de l’altitude, et d’écrire qu’elle a cette valeur :

On élève au carré, et on tire h :
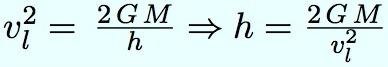
Application numérique, avec la valeur de la vitesse donnée plus haut :
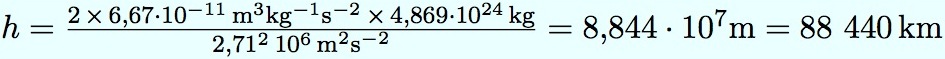
h est l’altitude à laquelle la vitesse de la sonde est égale à la vitesse de libération de la planète. Plus près, sa vitesse serait forcément inférieure à la vitesse de libération. Donc, elle doit passer plus haut. En regroupant ces deux contraintes, la sonde doit passer entre 88.000 et 1.000.000 km de Vénus. Plus près elle passera en restant dans cette fourchette, plus forte sera l’influence de Vénus.
Le problème est donc maintenant bien posé :
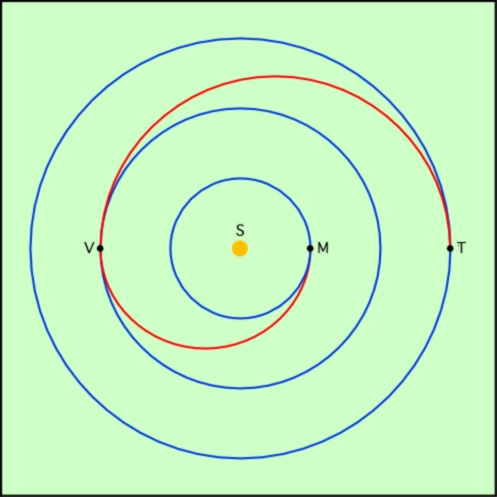
Les deux arcs d’orbite rouges semblent bien se raccorder, et c’est le cas car ils sont tagents à la même ellipse en un même point. Ils se raccordent donc en tant que courbes. Mais si on considère la vitesse de parcours de ces arcs, rien ne va plus. En effet, la vitesse d’arrivée depuis la Terre est de 37,73 km s-1, alors que la vitesse de départ vers Mercure est de 29,24 km = s-1.
On peut voir là deux problèmes :
Le trajet se compose donc de trois segments :
Ces trois arcs doivent être raccordés, et ne doivent pas présenter de changement de direction à leur articulation (les tangentes aux deux arcs aboutés doivent être parallèles).
Il y a une difficulté supplémentaire : l’arc d’hyperbole qui réalise l’assistance implique un changement de direction (l’entrée et la sortie ne sont pas parallèles). L’hypothèse que nous avions prise précédemment était que les deux arcs de Hohmann étaient tangents
En les séparant par un arc d’hyperbole, nous devons abandonner la tangence des arcs de Hohmann entre eux. N’étant plus tangents, ils ne le seront pas davantage avec l’orbite de Vénus. Ce ne seront plus exactement des arcs de Hohmann, ou tout au moins ils ne seront pas complets.
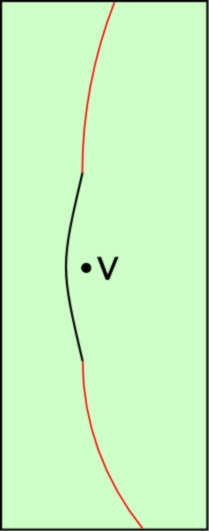
Sur ce schéma, on a abouté les deux arcs de Hohmann à un arc d’hyperbole intermédiaire, sans modifier les orientations (celle de l’hyperbole est naturellement centrée sur Vénus). On voit clairement les angles que font ces arcs entre eux, angles qui traduiraient des changements brusques de direction de la sonde, changements n’ayant aucune réalité physique.
Pour raccorder les arcs dans leur prolongement (angle nul), on a trois possibilités à prendre en compte.
Ceci est bien sûr approximatif, car la solution réelle ne passe pas par des arcs aboutés, mais par une continuité d’orbite qui se modifie progressivement. Mais l’explication reste adaptée.
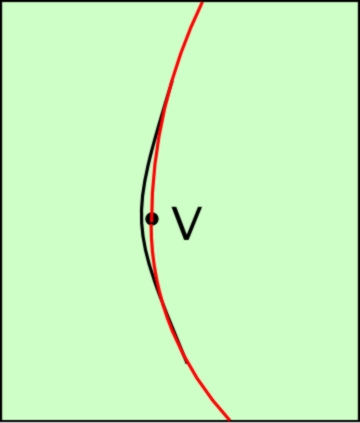
Ce schéma montre une trajectoire dans laquelle les deux arcs de Hohmann sont tronqués, et restent par ailleurs inchangés. Tout ceci illustre le principe de l’assistance gravitationnelle, mais les équations réelles du mouvement sont tout de même un peu plus complexes. La véritable solution consiste à écrire les équations du mouvement d’une sonde de masse négligeable, dans le champ gravitationnel combiné du Soleil et de Vénus (selon notre exemple). On utilise ces équations (différentielles) pour écrire un programme d’intégration numérique qui calcule pas à pas les positions successives de la sonde. A l’approche de Vénus, le champ de celle-ci augmente tout naturellement (par la plus grande proximité). Petit à petit, il devient prépondérant et le mouvement de la sonde se définit essentiellement par l’attraction de la planète. Puis, le point le plus proche étant passé, l’influence de la planète diminue, et celle du Soleil redevient prépondérante.
Où la sonde ira après dépend bien sûr de la partie de trajectoire avant approche. Si la cible est ratée, il faut modifier ces paramètres, et recalculer. On fait cela jusqu’à trouver la bonne trajectoire. L’approche que nous avons présentée plus haut peut dégrossir le problème, et fournir un jeu de paramètres approximatif pour démarrer les itérations du calcul.
Si on vise une planète supérieure, il faut disposer d’un relais assez massif pour servir de tremplin raisonnable. Ce n’est pas le cas de Mars, dont la masse est bien trop faible pour que l’assistance qu’elle pourrait produire soit significative. Ceci veut dire que pour aller vers Jupiter, on vise directement cette planète.
L’histoire change si on vise une planète plus lointaine. La masse de Jupiter est telle, que l’assistance gravitationnelle qu’elle peut fournir est énorme. Les planètes Saturne, Uranus et Neptune seront bien plus économiquement accessibles en passant par Jupiter.
Comment procède-t-on ?
Dans les formules établies plus haut, on a considéré l’arc de Hohmann pour aller d’une planète à une autre, et vu que les formules du demi grand-axe et de l’excentricité sont symétriques : que l’on aille de la Terre à Vénus, ou de Vénus à la Terre, les formules sont les mêmes. Seule leur interprétation change pour s’adapter à la situation.
Imaginons un voyage Vénus-Terre (retour d’échantillons de sol par exemple). Au départ de Vénus, la sonde se déplace sur la même orbite que la planète, à la même vitesse (35,02 km s-1). Elle doit accélérer pour atteindre 37,73 km s-1 (la vitesse de départ de Vénus vers la Terre est égale à celle d’arrivée de la Terre vers Vénus, puisque l’arc de Hohmann est la demi-ellipse tangente aux deux orbites).
Pour la même raison, l’arrivée vers la Terre est symétrique d’un départ de la Terre vers Vénus. Le voyage Vénus-Terre est donc facile à comprendre. Et un voyage Terre-Mars, ou Terre-Jupiter est semblable. Il est donc inutilie de les décrire en détail.
Dans les formules, comme il a été mentionné plus haut, R est toujours le rayon de l’orbite la plus grande, donc concerne toujours la planète la plus éloignée du soleil. r concerne la planète la plus proche.
Pour finir cette étude, déteminons les vitesses d’un voyage vers Jupiter. Les paramètres utiles sont :
| Terre | Jupiter | |
|---|---|---|
| vitesse | 29,79 km s-1 | 13,07 km s-1 |
| rayon orbital | 149,6 106 km | 778,4 106 km |
Départ : on utilise la formule (3), qui est pertinente pour l’arrivée vers une planète inférieure, ou le départ vers une planète supérieure.
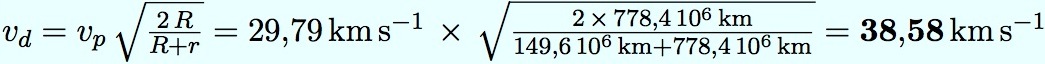
Arrivée : on utilise la formule (2), qui est pertinente pour le départ vers une planète inférieure, ou l’arrivée vers une planète supérieure.
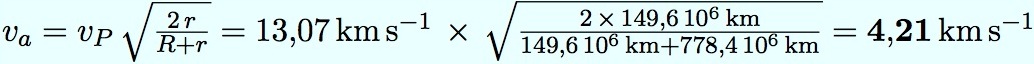
Nous avons considéré l’assistance gravitationnelle fournie par Vénus dans le voyage vers Mercure, en économisant le freinage au milieu du parcours. Mais on peut faire encore mieux ! Pourquoi ne pas utiliser l’assistance gravitationnelle de la Terre ? Imaginons lancer une sonde à destination de Vénus, en la plaçant d’abord sur une orbite très proche de celle de la Terre. Au bout d’un an à très peu près, la sonde va repasser à proximité de la Terre. On peut très bien s’arranger pour la faire passer dans la sphère de Roche, pour qu’elle subisse une influence. Et on comprend maintenant facilement qu’ainsi, on peut infléchir la trajectoire pour la précipter vers Vénus. C’est ce principe qui a été utilisé pour la sonde Messenger. Il est évident que cette méthode fait perdre un an à la sonde, temps qu’on aurait économisé avec une certaine quantité de carburant ! On ne peut pas gagner sur tous les tableaux…
Messenger devait freiner à l’approche de Mercure, et nous avons vu qu’il faudrait beaucoup de carburant (et le moteur pour l’utiliser). Pourquoi ne pas faire à l’arrivée ce qu’on a fait au départ ? Soit frôler Mercure pour infléchir la trajectoire de la sonde (abaisser son aphélie) afin de revenir vers la planète un tour de Soleil après, avec une vitesse relative plus faible. Mercure étant une petite planète, une assistance n’a pas suffi, et il a fallu trois survols avant d’envisager la satellisation (par une action d’un moteur).
Dans tout ce qui précède, on a considéré une sonde allant vers une planète. Mais on a lancé des sondes ayant d’autre buts. Par exemple la sonde Ulysses, destinée à l’observation du Soleil. On n’avait, avant elle, observé le Soleil que depuis le plan de l’écliptique. Il s’agissait pour cette nouvelle sonde, d’aller observer les pôles du Soleil. Pour les survoler, il fallait injecter la sonde sur une orbite perpendiculaire à l’écliptique. Or une telle orbite serait extrêmement coûteuse à atteindre. La solution a été de lancer cette sonde vers Jupiter, et de la faire passer sous la planète. L’assistance gravitationnelle a alors tourné le plan de l’orbite. Cette méthode est donc très pratique et très versatile. Elle peut s’adapter à de nombreuses situations, et on peut aussi la faire agir plusieurs fois de suite, avec des planètes différentes… avec évidemment l’allongement du temps de parcours !
---=OO=---