Historique de Marseille
| liens |
le 18/08/17
| Bonne année 2026 ! |
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
|||||
| �� Mécanique Quantique |
| |||||||
La Mécanique Quantique a été abordée dans d’autres chapitres, pour les nécessités de la compréhension de nombreux phénomènes. Le but du présent chapitre est de remettre certains de ces phénomènes dans un contexte historique qui apporte un éclairage très utile. Il est aussi d’apporter des précisions importantes et des détails sur des points délicats. Les différents aspects de la Mécanique Quantique seront donc revus ici.
On parle de quanta parce qu’une lumière monochromatique ne peut pas avoir toutes les intensités. S’il nous semble qu’on peut faire varier la quantité de lumière à volonté, c’est parce que la lumière que nous voyons est toujours de grande intensité : notre œil ne nous permet pas de voir de très très faibles éclairements. Mais l’effet photoélectrique, découvert par Hertz, montre qu’il y a un seuil de longueur d’onde, en-dessous duquel il ne se produit pas. Ceci prouve que certaines longueurs d’onde ont suffisamment d’énergie pour le provoquer, d’autres non. La lumière (l’énergie qu’elle transporte) n’arrive que par paquets.
Cette notion de paquet appelle celle de corpuscule : comme la masse est associée à une particule, un paquet d’énergie doit l’être également. C’est de là que vient la notion de photon (particule de lumière).
S’il n’y a qu’une seule couleur, c’est que tous les photons ont exactement la même énergie E = h ν, et par conséquent si on ajoute UN photon, on ajoute l’énergie h ν, et rien de moins. Un groupe de n photons de cette couleur possède l’énergie En = n h ν. Un groupe de n + 1 photons de même couleur possède l’énergie En+1 = (n+1) h ν = n h ν + h ν = En + h ν.
Il n’est pas possible d’ajouter une quantité d’énergie inférieure à h ν. C’est pourquoi on dit que l’énergie arrive par paquets.
Dans le contexte historique précité, le spectre de l’hydrogène a été étudié expérimentalement, en particulier par Hagenbach à Bâle. Il s’agit d’un spectre de raies, c’est-à-dire qu’il ne présente que quelques couleurs bien précises, et rien entre elles. Hagenbach a précisément mesuré les longueurs d’onde des diverses raies visibles. Aucune logique n’émergeait à l’époque entre ces longueurs d’onde, pour l’hydrogène et pour tous les autres éléments. Mais l’hydrogène étant le plus simple de tous, c’est lui qui a été choisi comme premier objet d’étude.
Hagenbach a donné la liste des longueurs d’onde à un professeur de la ville, Jean-Jacques Balmer, qui a trouvé une formule empirique les représentant. Cette formule n’expliquait rien, bien sûr, mais mettait en lumière un rapport entre les différentes radiations émises par l’hydrogène. Cette formule allait être capitale dans la compréhension du mécanisme d’émission, mais il fallait lui ajouter un principe, qui a été énoncé par Max Planck.
La formule de Balmer fait intervenir un entier n, numéro de la raie (celles-ci étant numérotées à partir de la raie rouge Hα) : 1 / λ = RH (1 / 22 - 1 / n2). Cet entier représente une notion fondamentale : le spectre de l’hydrogène n’est pas continu mais discret (le terme discret en mathématiques et physique signifie que deux valeurs sont séparées forcément par un intervalle vide). Alors qu’un spectre thermique montre une transition continue entre les différentes couleurs, le spectre d’émission de l’hydrogène ne montre que quelques couleurs précises.
D’après la formule de Balmer, Niels Bohr a supposé que l’électron tourne autour du proton (noyau), sur des orbites bien précises, auxquelles sont attachées des énergies bien définies. Il émet un photon lorsqu’il passe d’une orbite à une autre. Et l’énergie emportée par le photon est simplement la différence d’énergie entre les deux orbites d’origine et de destination de son saut.
Niels Bohr a posé une condition qui représente la quantification. Elle porte sur le moment cinétique de l’électron sur son orbite. Le moment cinétique est une notion classique importante, car dans le mouvement elle se conserve : sa valeur ne change pas dans toutes les variations de vitesse, d’accélération… que subit le mouvement, à la seule condition qu’il n’y ait pas de force extérieure appliquée au système.
Notons v la vitesse de l’électron sur son orbite, me sa masse. Le moment cinétique de rotation est défini comme la quantité de mouvement de l’électron P = me v, multipliée par le rayon de l’orbite : C = me v r.
La condition impose que ce moment cinétique soit un multiple entier d’une valeur, la constante de Planck. Par conséquent, la condition s’exprime par C = n ℏ.
Posant cette condition a priori, Niels Bohr en a étudié les conséquences, et vu qu’elles étaient en accord avec les observations. Cet accord justifie cette condition a posteriori. Nous allons voir maintenant comment on retrouve en particulier la formule de Balmer à partir de cette condition, puis plus loin, nous l’utiliserons comme base de la théorie quantique.
Il est très facile de calculer le rayon des orbites de l’électron dans le modèle de Bohr (vous pouvez sauter ce calcul, et considérer le résultat noté au-dessous ; mais remarquez bien l’utilisation de la condition). On considère les orbites circulaires, de rayon r. L’électron se trouve donc à la distance r du proton. ε0 est une constante de l’électrostatique (la permitivité du vide, et e la charge de l’électron. ℏ = h / 2 π est la constante de Planck réduite.
| L’électron subit une attraction électrostatique : | 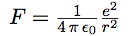 |
| En tournant, il subit également une force centrifuge (force fictive due à l’inertie) : | 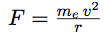 |
| Son orbite résulte de l’équilibre entre ces deux forces, qui sont donc égales : | 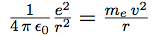 |
| Après simplification on obtient l’équation 1 : | 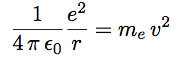 |
| Le moment cinétique de l’électron sur son orbite est : | 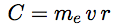 |
| Et la condition de quantification de Bohr : | 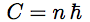 |
| En égalant ces deux expressions, on obtient l’expression de la vitesse de l’électron sur son orbite : | 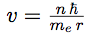 |
| Elevant la vitesse au carré, et la portant dans l’équation 1 il vient : | 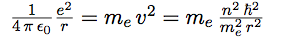 |
| Qui se simplifie en : | 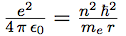 |
| On en tire enfin l’expression du rayon : | 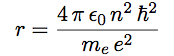 |
On voit que le rayon est proportionnel à n2.
Le calcul de l’énergie permet de déterminer les longueurs d’onde associées aux différents sauts de l’électron d’une orbite à l’autre. L’énergie totale de l’électron est la somme de son énergie potentielle et de son énergie cinétique.
| énergie potentielle | 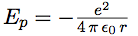 |
| énergie cinétique | 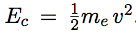 |
| Dans l’expression de l’énergie cinétique, reportons la vitesse obtenue dans l’équation 1 : | 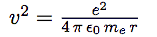 |
| On en tire l’énergie cinétique : | 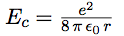 |
| On peut maintenant calculer l’énergie totale : | 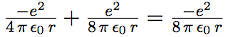 |
C’est la valeur absolue de l’énergie qui nous intéresse (le signe - nous rappelle qu’il faut fournir de l’énergie à l’électron pour l’arracher à l’atome).
| Reportons l’expression de r dans l’énergie correspondant à n : | 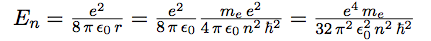 |
| En remplaçant ℏ par h / 2 π : | 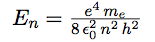 |
| On peut maintenant calculer les raies spectrales : | 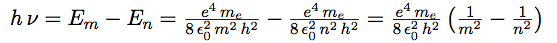 |
| Et obtenir la fréquence de l’onde : | 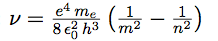 |
| On passe de la fréquence à la longueur d’onde par : | 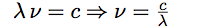 |
| d’où : | 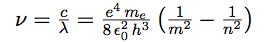 |
| et | 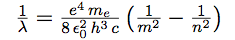 |
| On pose : | 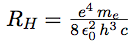 |
| Et on obtient l’expression recherchée : | 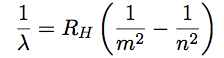 |
Remarquez que l’entier n dans cette formule provient de la formule donnant r, laquelle dérive de la condition de Bohr. C’est donc cette dernière qui définit les longueurs d’onde.
A partir des lois de la Mécanique Classique, et en ajoutant seulement la condition de Bohr, on retrouve donc la formule de Balmer donnant les longueurs d’onde des raies spectrales de l’hydrogène.
Jusqu’ici donc, il n’y a pas eu de bouleversement dans la Physique… Ceci parce qu’on s’intéresse toujours à la lumière seule !
L’étude approfondie de la lumière a donc montré qu’elle était à la fois ondulatoire (interférences, diffraction…), et corpusculaire (effet photoélectrique, rayonnement du corps noir…). Louis de Broglie a eu une intuition géniale, en ce sens particulièrement qu’elle était contre-intuitive. Il a imaginé qu’il pourrait en être de même de toutes les particules, et donc que les particules de matière pourraient avoir aussi une onde associée.
Il est surprenant de voir que la Mécanique Quantique, si différente de la Mécanique Classique, a été bâtie au départ en utilisant les lois classiques !
La formule de Balmer est empirique, et le modèle de Bohr est construit sur les lois classiques, modifiées par l’adjonction d’une contrainte pour introduire le caractère discret des orbites. Cet ajout est arbitraire, sans justification théorique. Le modèle marche, mais n’explique rien.
Louis de Broglie est parti d’une approche plus profonde. Les orbites de l’électron sont supposées circulaires, et il leur applique les lois de la mécanique classique. Mais il introduit la contrainte sous une forme bien plus physique. Il suppose que le moment cinétique C des orbites est quantifié : C = n ℏ.
On fait un calcul très simple, en utilisant les propriétés des orbites circulaires, et celles de ondes.
ATTENTION ! Dans le calcul qui suit, λ désigne la longueur d’onde de l’onde associée à l’électron, qu’il soit en orbite autour du noyau ou pas. C’est une propriété de l’électron lui-même et non pas, comme la lumière qu’il émet, une propriété de ses changements d’état.
| 1 | C = n ℏ | quantification du moment cinétique |
| 2 | C = P r | définition du moment cinétique d’une orbite circulaire |
| 3 | P = C / r | tiré de la ligne précédente |
| 4 | P = n ℏ / r | (1) reportée dans (3) |
| 5 | P = ℏ k | impulsion d’une onde, k est le vecteur d’onde |
| 6 | n ℏ / r = ℏ k | (4) = (5) |
| 7 | n / r = k | simplification |
| 8 | k = 2 π / λ | expression de k en fonction de la longueur d’onde |
| 9 | 2 π / λ = n / r | on égale les deux expression (7) et (8) |
| 10 | 2 π r = n λ | on réordonne |
| 11 | L = 2 π r | on reconnait la longueur de la circonférence |
| 10 | L = n λ | on obtient l’expression de L |
Le résultat indique que, le moment cinétique de l’orbite étant quantifié, la circonférence de cette orbite est égale à un nombre entier de longueurs d’onde. Ceci signifie que l’onde de l’électron, emportée avec lui, se retrouve exactement en phase après un tour. Elle interfère donc avec elle-même de manière constructive !
Si on considère une orbite qui ne vérifie pas cette propriété, elle interfère destructivement, et c’est ce qui explique que l’électron ne peut être stable sur une telle orbite.
Par conséquent, si l’électron emporte avec lui une onde, comme Louis de Broglie l’a supposé, il ne peut utiliser que ces orbites particulères. Le calcul montre que l’on retrouve ainsi exactement la formule de Balmer, et qu’on explique donc les raies de l’hydrogène. On explique aussi les raies des autres atomes, bien que le calcul se complique très vite.
Mais il y a mieux. Le deutérium est l’hydrogène lourd, dont le noyau comporte un neutron. Comment se présentent ses raies spectrales ?
Le modèle planétaire de l’atome de Bhor a été développé dans un contexte classique, en utilisant les lois classiques de la mécanique, et en leur ajoutant, pour répondre aux observations, une loi supplémentaire quantifiant les orbites.
Or le calcul que nous avons ébauché, qui est le calcul initial de Louis de Broglie, suppose que le proton (noyau de l’atome d’hydrogène) est parfaitement fixe. C’est une approximation tout à fait valable, puisque le proton est 1 840 fois plus lourd que l’électron, et donc, comme pour les planètes autour du Soleil, le petit corps perturbe peu le gros. Mais Louis de Broglie a cependant refait un calcul plus précis en tenant compte de l’entraînement du proton.
Notons mP la masse du proton. Soit ε = me / mP le rapport de la masse de l’électron à celle du proton. ε vaut à peu près 1 / 1 840. Alors, l’expression de la constante de Rydberg est légèrement modifiée : R = RH / (1 + ε).
Ceci n’a pas eu d’influence importante sur l’atome d’hydrogène, mais a permi la découverte du deutérium. Urey, en 1932, a observé que la raie Hα de l’hydrogène était flanquée, du côté violet, d’une raie faible à environ 2 Å. Cette raie s’explique simplement en considérant un noyau deux fois plus lourd que celui de l’hydrogène (le neutron et le proton ont pratiquement la même masse). Le rapport de masse de ce noyau ε′ = me / 2 mP = ε / 2 = 1 / 3 680. Les raies de ce noyau se trouvent donc décalées par rapport à celles de l’hydrogène de ε / 2.
Le spectre du deutérium a donc été découvert avant le deutérium lui-même. Et cette explication indique en même temps où se trouvent les raies de cet isotope de l’hydrogène.
Les relations d’incertitude d’Heisenberg ont été formulées en 1927 à partir d’une analyse de la notion de mesure. Mais elles proviennent plus profondément de la nature ondulatoire de la matière. Nous allons exposer successivement, de manière succinte, ces deux approches.
Lorsque Heisenberg s’est penché sur le problème de la mesure des grandeurs à l’échelle microscopique, il possédait la mécanique classique, dont les succès dans le système solaire étaient impressionants. L’idée la plus naturelle était évidemment d’appliquer ces principes à une échelle plus petite. Mais dans le cas des planètes, dont la masse est énorme, on peut très facilement mesurer simultanément la position et la vitesse. Alors, ces deux valeurs étant connues, l’applicaton des lois de la mécanique permet de prévoir la position et la vitesse à tout instant ultérieur. C’est le déterminisme de la Mécanique Classique.
Heisenberg a réfléchi à l’abîme immense qu’il y a entre la masse d’une planète et celle d’un électron. Comment mesure-t-on la position et la vitesse d’un électron ? Pour une planète, la lumière nous apporte ces informations. Qu’en est-il pour une particule ?
Pour éclairer une planète, il faut un grand nombre de photons. Chacun possède une énergie qu’il cède à la planète lorsqu’il vient la frapper. Mais cette énergie est négligeable par rapport à l’énergie cinétique d’une telle masse. Par contre, si le même photon vient frapper un électron, les choses se présentent d’une manière bien plus violente. L’énergie du photon perturbe gravement le mouvement de l’électron. On comprend bien alors qu’après avoir mesuré ainsi la position de l’électron, sa vitesse a été changée, et la mesure qu’on va en faire n’est plus exacte. Elle sera forcément entachée d’une erreur.
Heisenberg a supposé que la quantité de mouvement p de l’électron a été mesurée avec grande précision. Pour mesurer sa position, imaginons de l’observer avec un microscope. On sait qu’un instrument d’optique ne donne qu’une précision limitée par la longueur d’onde de la lumière utilisée. Cette précision est limitée à la moitié de la longueur d’onde : Δx = λ / 2. Pour faire la mesure de position, il faut qu’au moins un photon ait été dévié par l’électron, et viennent impressioner notre œil. Le choc subi par l’électron lui confère une énergie, celle du photon E = h ν. P = h / λ. Si le photon est renvoyé en sens inverse, sa quantité de mouvement change de signe. Pour cela, il faut l’arrêter, c’est-à-dire communiquer une impulsion p = h / λ, puis le renvoyer en sens inverse avec la même implusion, donc encore p = h / λ. Au total donc, l’électron aura acquis une impulsion de ΔPx = 2 h / λ (au maximum ; on ignore totalement dans quel sens le photon frappe l’électron, ce qui fait que l’impulsion acquise est comprise entre 0 et 2 h / λ).
Faisons le produit Δx ΔPx = λ / 2 × 2 h / λ = h. Puisque l’erreur ne peut pas être inférieure, on en déduit immédiatement que :
Δx × ΔPx ≥ h.
On nomme souvent les relations de ce genre relations d’incertitude. Cette appellation n’est pas bien correcte, parce qu’elle semble dire que nous ne sommes pas capables de faire les mesures, et que davantage de précautions pourraient donner un meilleur résultat. Le raisonnement précédent montre déjà le contraire, mais la seconde façon d’obtenir ces relations lève tout doute à ce sujet.
Cette approche est plus difficile à appréhender, car elle est plus mathématique. Elle s’appuie sur une analyse de l’onde que Louis de Broglie a associée aux particules de matière. Une onde sinusoïdale simple telle que sin ω t se traduit par un graphe infini dans les deux sens, donc par une onde d’extension infinie. Il n’est pas question de ça dans l’idée de Louis de Broglie. Au contraire, il s’agit d’une onde a portée très limitée. Ce n’est donc pas une sinusoïde simple.
L’onde associée à une particule matérielle doit être limitée à un petit domaine autour de celui-ci. Il faut donc trouver un moyen de construire une telle onde, mathématiquement, limitée.
On sait très bien que les ondes se mélangent par interférences, constructives ou destructives. Si on additionne deux ondes de fréquences différentes, on obtient une onde modulée. Et Fourier a montré qu’on peut très bien former une onde limitée à un petit domaine, nulle partout ailleurs, en ajoutant des ondes (en nombre infini). Plus précisément, si l’onde est non nulle entre t1 et t2, c’est-à-dire sur un intervalle de longueur Δt = t2 - t1, elle se représente par une somme d’ondes de pulsations ω telles que Δω × Δt ≥ 2 π.
La somme de toutes ces ondes s’appelle un paquet d’onde, et caractérise l’état d’une particule. Remarquez bien en effet qu’il ne s’agit par d’une onde simple, dont l’extension serait infinie, mais bien de la somme de toutes ces ondes élémentaires, chacune d’extension infinie, mais dont la somme n’est non nulle que dans l’intervalle considéré.
La relation E = ℏ ω permet d’écrire : ΔE / ℏ × Δt ≥ 2 π. D’où : ΔE × Δt ≥ 2 π × ℏ = h
ΔE × Δt ≥ = h
Nous avons retrouvé la même relation, par une méthode qui semble différente, mais qui est tout autant basée sur les propriétés mathématiques des ondes. Ces relations découlent donc de la nature ondulatoire de la matière, et sont incontournables. Nulle technique de mesure, si élaborée soit-elle, ne pourra les contourner.
L’existence du quantum d’action implique une sorte d’incompatibilité entre le point de vue de la localisation dans l’espace et dans le temps et le point de vue de l’évolution dynamique ; chacun de ces points de vue est susceptible d’être utilisé pour la description du monde réel, mais il n’est pas possible de les adopter simultanément dans toute leur rigueur. La localisation exacte dans l’espace et dans le temps est une sorte d’idéalisation statique qui exclut toute évolution et tout dynamisme ; l’idée d’état de mouvement prise dans toute sa pureté est par contre une idéalisation dynamique qui est en principe contradictoire avec les concepts de position et d’instant.
La Mécanique Classique partait de l’hypothèse que la position ET la vitesse d’un objet quelconque peuvent être mesurés avec la précision que l’on souhaite. C’est vrai dans le domaine macroscopique, mais pas pour l’étude des particules. Louis de Broglie explique la différence entre deux façons d’aborder les choses : soit on les considère statiques, et on mesure leur position ; soit on les considère dynamiques, et on mesure leur vitesse (exactement leur impulsion, produit de la masse par la vitesse). Ces deux points de vue, compatibles en Mécanique Classique, ne le sont plus en Physique des Particules.
La Mécanique Quantique est forcée d’utiliser un peu de ces deux approches pour décrire les phénomènes. La proportion de chacune est précisée par les relations d’Heisenberg. Vous remarquerez que la plus connue de celles-ci, Δx ΔPx ≥ ℏ, relie deux variables x et Px, la première étant une variable de position, traduisant le point de vue statique, la seconde Px étant une variable de mouvement, conformément au second point de vue. Et l’inégalité montre que si on augmente la prise en compte du point de vue statique (en diminuant l’incertitude sur x), on diminue forcément l’importance du point de vue dynamique, en augmentant l’incertitude sur Px.
Les inégalités d’Heisenberg montrent donc la balance entre ces deux points de vue.
Partant du principe que chaque particule possède une onde associée, et que cette onde ne s’étend pas à l’infini, il s’agit de construire mathématiquement cette onde. En évitant au maximum les formules, nous allons tout de même essayer de montrer visuellement comment les choses se passent.
On connait la forme d’une sinusoïde, courbe représentant la fonction sinus. On peut définir la somme de deux fonctions en additionnant simplement leurs valeurs en chaque point. Ainsi, on peut additionner deux sinusoïdes. Ou plus… Le résultat se voit sur l’animation ci-dessous :
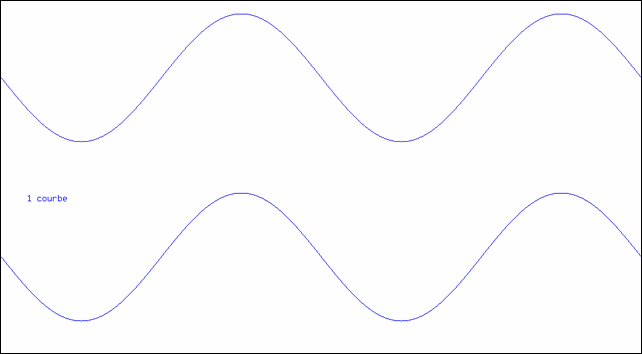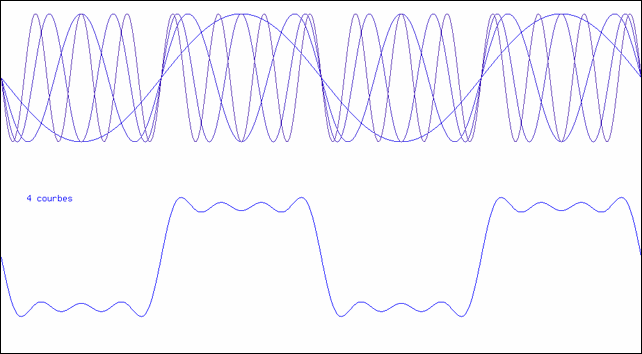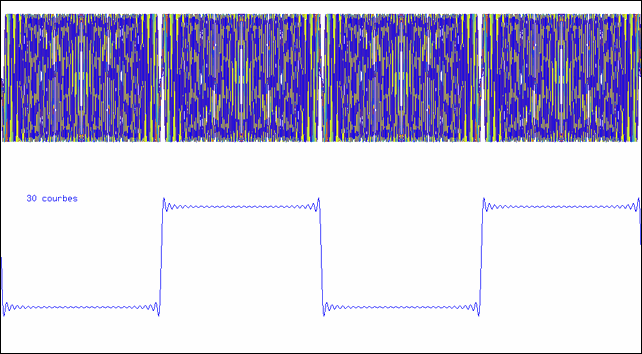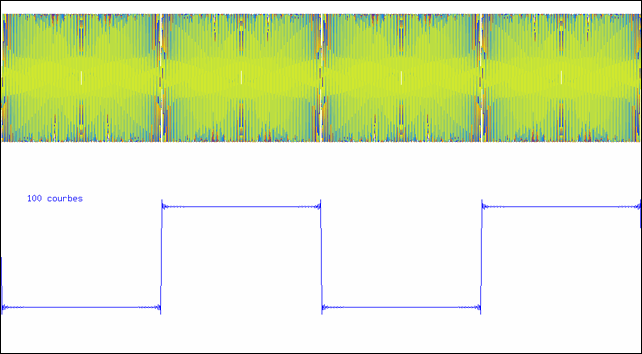
Addition de sinusoïdes
L’animation montre comment on peut synthétiser une courbe en créneau à l’aide d’un nombre suffisant de sinusoïdes. La partie supérieure montre la superposition des sinusoïdes ; la courbe inférieure est leur somme.
| nb courbes | somme | |
|---|---|---|
| 1 | f1(t) = sin(ω t) | |
| 2 | f2(t) = sin(ω t) + 1/3 sin(3 ω t) | |
| 3 | f3(t) = sin(ω t) + 1/3 sin(3 ω t) + 1/5 sin(5 ω t) | |
| … | … |
Sur l’animation, on voit immédiatement que, plus on ajoute de termes, plus la courbe prend la forme d’un créneau.
Ces fonctions représentent le spectre de la fonction considérée. Pour la fonction f2(t) = sin(ω t) + 1/3 sin(3 ω t) par exemple, le spectre comprend deux raies : ω et 3 ω, avec les amplitudes respectives 1 et 1/3. On peut compléter le tableau précédent :
| nb courbes | somme | raies | amplitudes | |||
|---|---|---|---|---|---|---|
| 1 | f1(t) = sin(ω t) | ω | 1 | |||
| 2 | f2(t) = sin(ω t) + 1/3 sin(3 ω t) | ω, 3 ω | 1, 1/3 | |||
| 3 | f3(t) = sin(ω t) + 1/3 sin(3 ω t) + 1/5 sin(5 ω t) | ω, 3 ω, 5 ω | 1, 1/3, 1/5 | |||
| … | … | … | … |
La dernière courbe représentée dans l’animation est la somme de 100 sinus ; elle a donc un spectre contenant les 100 raies ω, 3 ω, 5 ω,…, 100 ω. Vous remarquez qu’elle est toujours périodique, et que sa période est la même que celle de la première sinusoïde (ω). Si cette fonction était injectée dans un amplificateur, on entendrait un son correspondant à cette fréquence. Quand à la nature du son, il serait d’autant plus riche qu’il y a plus de termes : la première fréquence, la plus basse, est le fondamental, les autres sont les harmoniques (multiples du fondamental).
On peut représenter sur un graphique le spectre correspondant :
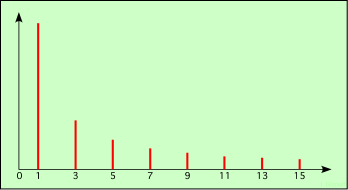
spectre de la fonction porte
Les traits verticaux rouges représentent chacun une raie spectrale. Leur position (1, 3 …) indique la pulsation (équivalente à la longueur d’onde) de la raie ; leur hauteur indique l’amplitude de la raie (son intensité).
On a donc réussi à fabriquer, par addition de sinusoïdes, une courbe qui reproduit à l’infini un paquet d’ondes ! Il faut maintenant le limiter à une seule copie.
Tant qu’on sommera des sinusoïdes écartées (laissant un trou entre 3 ω et 5 ω par exemple), on obtiendra toujours une fonction périodique. Même en additionnant une infinité de sinusoïdes. Il faut donc accepter de supprimer les trous entre deux raies, et par conséquent de passer d’un spectre de raies, à un spectre continu !
La question est donc de savoir si on doit considérer toutes les valeurs possibles de ω, ou si on peut se limiter à un intervalle par exemple.
La méthode mathématique utilisée pour trouver les raies spectrales plus haut est basée sur les séries de Fourier, qui font une addition discrète (avec des trous entre les fonctions additionnées). Il faut généraliser en supprimant les trous, ce qui se fait en passant d’une somme à une intégrale. Mais le but ici n’est pas de faire des calculs, et nous allons préciser le résultat que l’on veut atteindre :
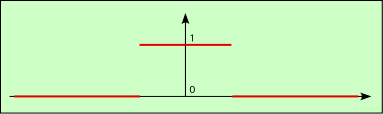
fonction porte
La fonction représentée ci-dessus représente un seul créneau. Elle vaut 1 autour de l’axe vertical, et 0 partout ailleurs. C’est elle que nous voulons représenter.
Un petit calcul que nous ne ferons pas ici montre que le spectre de cette fonction n’est plus un ensemble de raies munies de leurs amplitudes, mais une nouvelle fonction, qui nous donne l’amplitude correspondant à chaque valeur de ω :
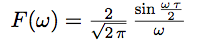
On voit apparaître un rapport de sin ω et ω. Cette fonction joue donc un grand rôle, et on la nomme sinus cardinal.
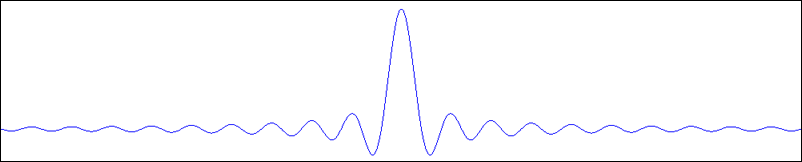
La courbe représente la fonction sinus cardinal, définie par sinC(x) = sin(x) / x. A priori, elle n’est pas défine au point x = 0 (à cause de la division par 0), mais elle est continue à gauche et à droite de 0, et les limites sont égales à 1. On peut donc la prolonger par continuité par sinC(0) = 1. Sa courbe est parfois nommée courbe sombrero, pour une raison évidente !
On peut voir que cette courbe présente une valeur élevée au voisinage de 0, mais que ses valeurs diminuent rapidement en s’en éloignant, du côté négatif comme du côté positif. Puisqu’elle représente le spectre de la fonction porte, on comprend bien que seules les fréquences autour de 0 sont utiles.
C’est par un tel procédé qu’on définit le paquet d’onde en Mécanique Quantique.
Mais là ne s’arrête pas la question. Quelle est la largeur de l’intervalle de fréquences à considérer ? Y a-t-il une relation entre cette largeur et la largeur de la fonction porte elle-même ?
La réponse est capitale, et elle est affirmative !
On démontre en effet que :
Δω est la largeur de l’intervalle de fréquences ; Δt est celle de l’intervalle de temps considéré.
Reprenons la relation fondamentale que Louis de Broglie a utilisée en associant une onde à chaque particule :
E = h ν = h ω / 2 π (puisque ω = 2 π ν) = ℏ ω
Soit ω = E / ℏ et donc Δω = ΔE / ℏ
Remplaçons Δω par cette valeur dans l’inégalité encadrée ci-dessus :
ΔE / ℏ × Δt ≥ 2 π
ΔE × Δt ≥ 2 π ℏ = h
On vient de démontrer la première des relations d’incertitude d’Heisenberg…
Bien qu’Heisenberg ait obtenu ces relations par une analyse des perturbations que l’on produit sur une particule en l’observant, elles proviennent de la nature ondulatoire profonde de la matière. Et elles sont donc incontournables : nul progrès ne pourra nous en affranchir !
Le paquet d’onde associé à une particule, doit être lié à elle, et donc se déplacer avec elle. Considérons le système de coordonnées lié à la particule. Dans ce système, il est évident que l’onde est au repos, donc stationnaire (sin ω t). Mais si on considère un repère par rapport auquel la particule (avec son onde), se déplace à la vitesse v, l’application de la transformation de Lorentz à l’onde montre qu’elle devient progressive, c’est à dire qu’elle se déplace dans ce système (utiliser la transformation du temps, et la reporter dans le sinus). Et on obtient simultanément la vitesse d’entraînement, qui est évidemment celle de la particule.
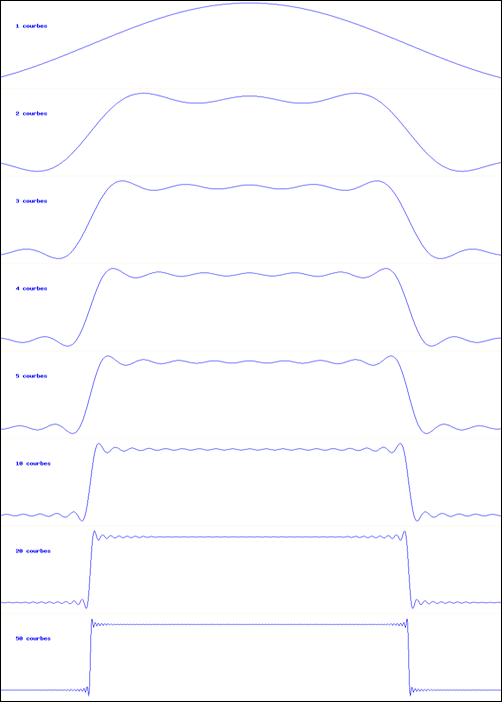
La fonction tracée est la somme :
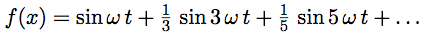
Vous remarquerez qu’elle est périodique. Le créneau se répète à l’infini.
Considérons un essaim d’abeilles. Il est impossible de déterminer la trajectoire de chaque abeille. Pourtant la trajectoire de l’essaim entier est facile à décrire. Il en est de même avec les particules. Chacune nous échappe dans le détail de son mouvement, mais l’ensemble, qui constitue un objet macroscopique, se laisse bien décrire par les lois de la Mécanique Clasique.
Si la Mécanique quantique recèle un mystère, ce n’est pas dans la quantification elle-même, ni dans le Principe d’Incertitude qu’il faut le rechercher. Les deux sont la conséquence de l’association d’une onde à chaque particule.
Le mystère, s’il y en a un, se trouve donc dans cette onde qui accompagne la particule. Mais ce n’est un mystère que parce que nous sommes très gros ! Nous sommes constitués de milliards de milliards de particules, et à notre échelle, les mécanismes quantiques probabilistes sont moyennés et deviennent naturellement les lois certaines de la Physique Classique, celles auxquelles nous sommes habitués, et que nous trouvons naturelles….
---=OO=---