L’actualité du LAM	Le cours à l’Observatoire Historique de Marseille	… …	liens - alphabet grec bibliographie fiches lexique multiplicateurs tableau périodique	Mis à jour le 18/08/17
Temps thermique

Le temps thermique, ou temps de Kelvin-Helmholtz, est le temps pendant lequel l’objet peut rayonner sur ses réserves d’énergie gravitationnelle, en se contractant lentement.

Temps de Kelvin-Helmholtz

L’énergie gravitationnelle produite par la contraction alimente le rayonnement du nuage d’une part, et le chauffe d’autre part. Le théorème du viriel, assez fondamental en thermodynamique, indique les proportions : la moitié est rayonnée, l’autre moitié sert pour le chauffage.

Le nuage se contracte, mais sa température est restée très basse, beaucoup trop basse pour déclencher la fusion de l’hydrogène. Aussi, pendant cette nouvelle étape, la source d’énergie sera encore la gravitation.

La luminosité L d’une étoile est l’énergie rayonnée par unité de temps. Donc, l’énergie E_r rayonnée par l’étoile en formation dans une durée τ_KH est :

E_r = L τ_KH

Le théorème du viriel nous dit que cette énergie est la moitié de l’énergie potentielle ΔE_p produite dans le même temps :

E_r = L τ_KH = ΔE_p / 2

On en déduit le temps : τ_KH = ΔE_p / 2 L

L’énergie potentielle s’exprime en fonction du rayon de l’étoile : ΔE_p = G M² / R

d’où :

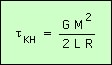
τ_KH est le temps de Kelvin-Helmholtz.

Exemple

Imaginant un instant que le Soleil ne fusionne plus l’hydrogène, et que l’énergie gravitationnelle soit sa seule source. Pendant combien de temps brillerait-il encore ?

Le rayon du Soleil est de 6,9599 10⁸ km = 6,9599 10¹¹ m ; sa luminosité est de 3,846 10²⁶ W , et sa masse vaut 2 10³⁰ kg. L’application de la formule donne :

τ_KH = 6,673 10^-11 m³ kg^-1 s^-2 × (2 10³⁰ kg)² / (2 × 3,846 10²⁶ W × 6,9599 10¹¹ m) = 26,692 10⁴⁹ / 53,5355 10³⁷ = 0,4986 10¹² s = 15,81 millions d’années

C’est 300 fois moins que les 5 milliards d’années depuis lesquelles le Soleil brille. La présence de la vie sur Terre (fossiles) atteste que le Soleil émet la même quantité de lumière depuis plusieurs centaines de millions d’années, ce qui suffit à éliminer la source gravitationnelle seule. Donc la contraction gravitationnelle ne saurait en aucun cas expliquer que le Soleil ait brillé aussi longtemps dans le passé.

Reprenons le nuage d’hydrogène précédent, au terme de sa contraction en chute libre. Supposons qu’il brille autant que le Soleil (en réalité, une étoile à ce stade brille davantage). Les parties externes sont encore en chute, alors que le cœur a atteint l’équilibre mécanique. C’est le rayon de ce cœur qu’il faut prendre en compte. Le nuage complet a un rayon de 5 10¹³ m ; prenons le centième de ce rayon pour le cœur : 5 10¹¹ m. Alors :

τ_KH = 6,673 10^-11 × (2 10³⁰)² / (2 × 3,846 10²⁶ × 5 10¹¹) = 26,692 10⁴⁹ / 38,46 10³⁷ = 0,694 10¹² s = 22.000 ans.

Sans nous attarder à la valeur trouvée, nous pouvons constater qu’elle est d’un ordre de grandeur supérieure à la chute libre, mais toujours très petite par rapport à la vie du Soleil.

---=OO=---