Historique de Marseille
| liens |
le 18/08/17
| Bonne année 2026 ! |
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
|||||
| �� Etoiles à neutrons |
| |||||||
Les étoiles à neutrons sont des objets compacts, les seconds après les naines blanches par ordre de densité croissante. Comme les naines blanches :
Les étoiles à neutrons sont des objets à la fois théoriques et observés. Prévus par le calcul, ils ont étés découverts sous différentes formes, dont la plus connue est le pulsar.
Lorsque la densité est très forte, les électrons ne supportent plus le poids, et l’objet se contracte. Les électrons se rapprochent des noyaux, et peuvent même y pénétrer à la faveur d’une réaction β transformant un proton en neutron :
p + e- → n + νe (1)
p : proton, e- : électron, n : neutron, νe : neutrino électronique.
Mais le neutron n’est pas une particule très stable, et il se désintègre selon la réaction inverse :
n → p + e- + ![]() e (2)
e (2)
Ces deux réactions constituent un processus d’équilibre, l’une annulant l’effet de l’autre.
Elles peuvent s’appliquer à un nucléon faisant partie d’un noyau. Considérons donc un noyau A
ZX ayant Z protons (ce qui définit l’élément chimique auquel il appartient), et A nucléons. Par exemple 4
2He. Les deux réactions le transforment de la manière suivante :
A
ZX + e- → A
Z-1X + νe
A
Z-1X → A
ZX + e- + ![]() e
e
Dans la première réaction, un proton du noyau absorbe un électron, et se transforme en neutron. Le noyau a donc un proton de moins, il lui en reste Z-1. Puisque le proton s’est transformé en neutron, le noyau a un proton de moins, et un neutron de plus, donc le même nombre A de nucléons. La seconde réaction fait l’inverse.
La première fait disparaître un électron, la seconde en crée un ; et ces deux réactions sont en équilibre. Mais cet équilibre va être rompu.
Dans le cœur d’une étoile massive, les électrons libres constituent un gaz dégénéré dans lequel baignent les noyaux. Un état dégénéré est un état dans lequel tous les niveaux d’énergie quantiques les plus bas sont occupés. Lorsque la pression est très forte, il ne reste plus de niveaux de faible énergie. La seconde des deux réactions, ne pouvant en général produire un électron de très haute énergie, se trouve bloquée. Mais la première n’est pas affectée.
Ce processus qui tend à remplacer les protons par des neutrons dans une matière dégénérée se nomme neutronisation.
Il s’ensuit que les électrons peuvent être absorbés par les protons dans le processus β de la première réaction, transformant les protons en neutrons, mais ensuite ces neutrons ne peuvent plus redevenir protons.
Les noyaux conservent le même nombre de nucléons (masse atomique A constante), mais leur nombre de protons décroît. Alors, leur énergie de liaison diminue, et ils finissent par se briser. A une densité de 1014 g cm-3, ils sont tous brisés, et les neutrons sont libres. Dans des conditions normales, le neutron libre n’est pas stable, et se désintègre spontanément par la réaction 2. Mais dans les conditions qui règnent dans ces objets compacts, le neutron est stable.
La faible probabilité (non nulle) de produire un électron de haute énergie dans la réaction 2 permet de maintenir un taux de 0,5 % de protons et d’électrons.
Outre la conversion des protons en neutrons, le processus URCA produit des neutrinos électroniques. Ces neutrinos équilibrent la balance énergétique de la réaction :
énergie(A
ZX) + énergie(e-) = énergie(A
Z-1X) + énergie(νe)
Or le neutrino, particule fantôme, passe à travers l’étoile et s’échappe, emportant son énergie. Le bilan énergétique de la réaction, pour l’étoile, est donc négatif. Ce mécansime est très efficace, du fait de la très faible section efficace du neutrino. L’étoile perd énormément d’énergie, en très peu de temps.
Pour maintenir son équilbre hydrostatique, elle a besoin de produire beaucoup d’énergie au centre. Cette perte accélère donc la contraction, qui se tourne en effondrement.
L’effondrement s’arrête lorsque, les protons ayant été changés en neutrons, l’étoile est devenue un gaz de fermions. Les neutrons jouent dans l’étoile à neutrons, le même rôle quantique que les électrons dans les naines blanches. La pression quantique de dégénérescence bloque la contraction, à condition que la masse ne soit pas trop forte. Les neutrons peuvent supporter jusqu’à 3 M.
Le processus URCA conduit à :
- transformer les protons en neutrons ;
- évacuer l’énergie par les neutrinos, en provoquant l’effondrement.
Le nom du processus a une origine qui vaut la peine d’être contée ! Le difficile problème de l’explosion d’une supernova a été résolu en partie, par la découverte de ce mécanisme, à Rio de Janeiro. La particularité du phénomène est la disparition, qui semblait bien mystérieuse, de l’énergie. Or il existait à Rio un casino un peu particulier, où l’argent des joueurs s’évaporait de façon tout aussi mystérieuse... Le nom du casino a été donné par analogie à ce groupe de deux réactions.
Quelques temps plus tard, les autorités, ayant eu connaissance de cette analogie, ont fermé le casino !
L’étoile à neutrons se forme à très haute température, de l’ordre de 10 milliards de degrés. Un fort flux de neutrinos entraîne un refroidissement très rapide, qui amène l’étoile à 1 milliard de degrés seulement (!) en une journée. Le refroidissement se ralentit ensuite, et il faut un siècle pour diviser encore par 10 la température, ce qui donne 100 millions de Kelvins.
Au début de l’effondrement, la pression est produite presque exclusivement par les électrons dégénérés. Plus la densité augmente, plus les électrons sont capturés par les protons pour donner des neutrons (avec émission de neutrinos). Les électrons sont ainsi progressivement remplacés par des neutrons, et finalement c’est la pression de dégénérescence des neutrons qui produit pratiquement la pression totale. La densité centrale est alors de 2 1013 g cm-3. A plus haute densité, 2,4 1014 g cm-3, les noyaux sont pratiquement au contact, et perdent leur individualité. Il reste un gaz de neutrons, contenant quelques protons et électrons (de l’ordre de 1 %).
L’équilbre d’une étoile à neutrons est assuré par le principe d’exclusion de Pauli, comme dans les naines blanches, mais appliqué ici aux neutrons (qui sont aussi des fermions).
Tout comme dans les naines blanches, il existe une masse limite, au-dessus de laquelle la pression quantique des neutrons ne peut plus supporter la gravité, et l’objet s’effondrera encore plus, pour former un trou noir. La limite se situe là où la vitesse quantique d’un neutron approche la vitesse de la lumière, ce qui correspond à une densité de l’ordre de 6 1015 g cm-3. La masse limite correspondante se situe autour de 3 masses solaires. On la nomme masse d’Oppenheimer-Volkov, du nom des premiers physiciens l’ayant déterminée.
La construction d’un modèle d’étoile à neutrons est difficile, et reste un peu floue, car il est impossible de reproduire en laboratoire les conditions qui y règnent. On n’a jamais observé directement le gaz de neutrons qui constitue le centre de l’étoile.
La nature précise de l’interaction forte n’est pas connue à très courte distance : on sait qu’elle est attractive à des distances de l’ordre du fermi (distance entre deux nucléons dans la matière normale), et devient répulsive plus près, vers 0,3 fermi. Lorsqu’elle est attractive, elle diminue la pression, et lorsqu’elle est répulsive, elle l’augmente.
Les moyens techniques actuels ne permettent pas de déterminer le potentiel d’interaction forte à des distances plus courtes encore, qui sont à considérer lorsque la masse du cœur dépasse les 3 M. Ceci se traduit par une incertitude sur les propriétés de ces objets.
La rotation, bien que très rapide, n’affecte pas la masse maximum. La gravité est si forte, que la force centrifuge reste négligeable, sauf peut-être dans un pulsar ultra-rapide.
Lorsqu’on parle de la masse d’une étoile à neutrons, il faut considérer deux choses différentes :
La différence entre les deux est l’énergie de liaison, et correspond à l’énergie qui a été libérée au cours de la contraction. La masse sensible, qui influence gravitationnellement les astres environnants, est plus petite que la masse qui a formé l’étoile.
Les hypérons sont des particules, semblables à des nucléons lourds. Ce sont tous des fermions (spin demi-entier), qui obéissent à la statistique de Fermi-Dirac (donc obéissent au principe d’exclusion de Pauli). Ils interagissent par interaction forte (ce sont des hadrons).
Les hypérons sont constitués, comme les nucléons, de trois quarks, incluant un quark étrange s (proton = uud, neutron = udd). Les hypérons sont donc des particules étranges.
Ils sont instables, et se désintègrent en proton, neutron ou méson en 10-10 à 10-8 seconde.
Quelques hypérons : Δ, Λ, Ξ et Ω.
On trouve des hypérons dans les rayons cosmiques, et on en produit dans les accélérateurs de particules. La masse des hypérons étant plus grande que celle des nucléons, les hypérons sont moins stables, et nécessitent beaucoup plus d’énergie pour produire une paire hypéron-antihypéron.
Lors de l’effondrement, les principaux paramètres physiques de l’étoile sont conservés. Ainsi, le moment cinétique de rotation ne change pas, alors que le rayon diminue fortement. Ceci entraîne une très forte accélération de la rotation, qui amène l’étoile à neutrons à tourner, d’après les calculs, en un temps de l’ordre de la seconde !
Bien sûr, la gravité extraordinaire qui règne à la surface de cet objet empêche la force centrifuge de projetter sa matière dans l’espace. Une telle vitesse de rotation est donc parfaitement possible.
Un autre paramètre physique conservé est le champ magnétique. Comprimé dans un volume beaucoup plus petit, son intensité à la surface devient très grande.
Lorsque la densité devient suffisante, l’énergie correspondante permet la création de paires hypéron-antihypéron. On nomme cette transformation hypéronisation du cœur de l’étoile. Il a une influence sur les propriétés physiques, conséquences mal connues.
Une autre désintégration devient possible lorsque la densité atteint le double de la densité nucléaire :
n → p + π-
Or les π sont des bosons, et tendent à se placer tous dans le même état quantique d’énergie minimum, donc de vitesse nulle. On appelle un tel ensemble de bosons un condensat de Bose-Einstein. Dans cette réaction, un neutron (fermion) a disparu, au profit d’un π (boson), donc la pression quantique diminue.
Un autre problème des modèles concerne la proximité des particules. Pour représenter correctement leurs interactions, il faut résoudre le problème des n-corps, comme en mécanique céleste. Ce problème ne peut pas se résoudre de manière analytique.
Toutes ces difficultés produisent une incertitude importante dans les modèles d’étoiles à neutrons. En fait, selon le choix que l’on fait pour le potentiel, les propriétés changent. Mais il est intéressant de noter que l’observation peut, parfois, interdire certains modèles. Il est possible qu’on obtienne ainsi des renseignements sur la physique même de ces particules, dans des conditions inaccessibles au laboratoire.
Par exemple, le pulsar binaire PSR 1913+16 est une étoile à neutrons de 1,42 M. Tous les modèles (définis par une équation d’état) qui prévoient une masse limite en-dessous de cette valeur sont donc invalidés.
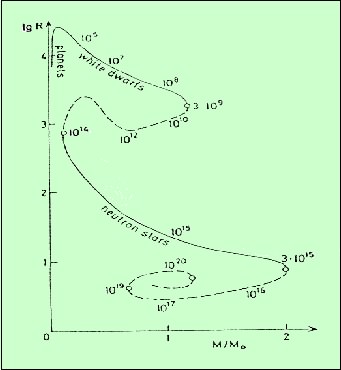
Relation masse-rayon, des planètes aux trous noirs
Les valeurs ci-dessous sont calculées pour une étoile à neutrons de 1,4 M. Son rayon est de l’ordre de 10 km.
Les étoiles à neutrons ont une atmosphère, si l’on peut nommer ainsi la fine enveloppe gazeuse qui les entoure. La gravité à la surface (g = 1,3 1014 cm s-2) est 10 milliards de fois supérieure à celle du Soleil (g = 2,7 104 cm s-2) ! Aussi, l’atmosphère n’est qu’une infime couche de quelques centimètres de gaz, à une température de plusieurs millions de degrés. La matière n’y est pas dégénérée.
Sous l’atmosphère, se trouve une surface solide ! C’est assez inhabituel pour une étoile, et ce simple fait suffirait à les rendre extraordinaires. Il s’agit d’une croûte métallique, constituée essentiellement de fer, dont l’épaisseur totale n’est que de 900 mètres. Sa masse volumique est de 106 g cm-3 à la surface, et atteint 2,4 1014 g cm-3 à la base. Les atomes de fer forment un treillis, qui produit la structure cristalline. L’arrangement des noyaux de fer dans ce treillis lui assure une énergie d’interaction coulombienne minimale, et cette matière ressemble à celle qui forme l’intérieur d’une naine blanche. Elle est divisée en deux parties, la séparation se trouvant à une profondeur de 300 mètres, lorsque la masse volumique atteint 4 1011 g cm-3. Au dessous de cette limite, les noyaux de fer, toujours arrangés en réseau cristallin, baignent dans un gaz de neutrons et d’électrons libres. A la base de cette croûte, tous les noyaux sont détruits, et les neutrons sont tous libres. La destruction des noyaux se fait progressivement avec la profondeur croissante.
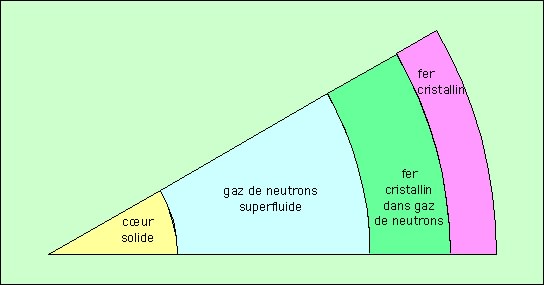
Sous la croûte se trouve la soupe de neutrons. La masse volumique est supérieure à 2,4 1014 g cm-3. Elle est mélangée à une faible quantité de protons et d’électrons qui subsistent. Le gaz de neutrons est bien évidemment dégénéré, et superfluide. Le gaz de protons est de son côté superconducteur, ce qui devrait avoir une grande importance en considérant le champ magnétique. L’étendue de cette zone est d’une dizaine de kilomètres.
Enfin, il est possible - mais on n’en a pas la certitude - qu’il y ait un noyau solide au centre, d’un kilomètre de diamètre. Si c’est le cas, les neutrons doivent y former une structure cristalline. La masse volumique centrale atteint 1,3 1015 g cm-3.
On n’a pas observé directement une étoile à neutrons. Sa petite taille et sa faible brillance nous en empêchent. Mais la découverte des pulsars, puis leur intreprétation, ont donné une observation indirecte.
---=OO=---