L’actualité du LAM	Le cours à l’Observatoire Historique de Marseille	… …	liens - alphabet grec bibliographie fiches lexique multiplicateurs tableau périodique	Mis à jour le 17/08/17
Jour solaire

Une planète se caractérise, entre autre, par ses durées de révolution autour du Soleil (année), et de rotation sur elle-même (jour).

L’une et l’autre sont mesurées par rapport à un repère réputé fixe : les étoiles. Le jour ainsi défini se nomme jour sidéral.

Le jour solaire est la durée qui ramène le Soleil deux fois successives au méridien. Mais nous verrons que cette définition, qui nous semble très claire en bons terriens que nous sommes, ne le serait pas forcément si nous vivions sur une autre planète ! De plus, même sur Terre, cette durée est variable au cours de l’année ; on l’appelle alors jour solaire vrai. Pour des raisons de commodité, on définit le jour solaire moyen. Celui-ci est donc invariable ; c’est lui qu’on utilise en disant que l’année tropique terrestre dure 365,2422 jours (solaires moyens). Une durée exprimée en ces termes est immédiatement convertible en secondes, la seconde étant l’unité de temps définie par des moyens optiques, indépendants des mouvements de la Terre. Le jour solaire vrai étant variable, sa durée ne correspond pas toujours au même nombre de secondes au cours de l’année.

Sur les schémas ci-dessous, la planète est représentée par un disque noir. Le petit trait indique la direction du zénith pour un observateur particulier (le point du ciel au-dessus de sa tête). De plus, on représente l’ensemble vu du côté nord de l’orbite (on observe les pôles nord de la planète et du Soleil). Le mouvement orbital et la rotation de la planète sur elle-même se feront tous dans le même sens direct.

Première situation

• Pour simplifier, considérons d’abord le cas d’une planète qui ne tournerait pas autour du Soleil, et donc resterait toujours à la même place par rapport aux étoiles (bien sûr, une planète réelle dans cette situation ne pourrait que tomber sur le Soleil…). Le mouvement du Soleil dans le ciel serait alors dû exclusivement à la rotation de la planète sur elle-même ; or en un jour sidéral, elle tourne de 360°. par rapport aux étoiles. Puisqu’elle ne bouge pas par rapport au Soleil, elle accomplira aussi 360°. par rapport au Soleil. Donc elle accomplira un jour solaire exactement. Par conséquent, dans une telle situation, jour solaire = jour sidéral. Bien sûr, le Soleil, fixe par rapport aux étoiles, semble tourner dans le même sens et à la même vitesse qu’elles.

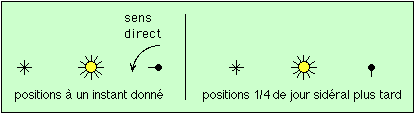
Dans le schéma de gauche, le Soleil et l’étoile sont au zénith pour cet observateur ; à droite, le Soleil et l’étoile sont à l’horizon et se couchent. On voit donc qu’il s’est écoulé un 1/4 de jour sidéral, et aussi 1/4 de jour solaire. Les deux durées sont égales.

Attention, le Soleil semble tourner dans le sens inverse ! Donc si la planète tourne d’un angle j (j est la rotation sidérale de la planète), le Soleil tourne dans le ciel d’un angle -r. Si la planète tourne dans le sens direct, le Soleil montre un mouvement apparent rétrograde dans le ciel.

Deuxième situation

• Considérons maintenant une seconde situation hypothétique dans laquelle la planète tourne autour du Soleil d’un mouvement circulaire uniforme (excentricité de l’orbite nulle). Supposons encore que cette planète ne tourne pas sur elle-même par rapport aux étoiles (rotation sidérale nulle). Le mouvement du Soleil dans le ciel serait dû exclusivement au déplacement de la planète sur son orbite. Lorsque la planète aura tourné d’un angle v autour du Soleil (v est l’anomalie vraie), celui-ci se sera déplacé d’une même quantité dans le ciel. On voit aussi que le Soleil tourne apparemment dans le sens direct.

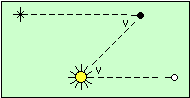Le Soleil et l’étoile sont au zénith.	La planète a tourné d’un angle v autour du Soleil ; elle n’a pas tourné par rapport à l’étoile. Le Soleil a tourné d’un angle v dans le ciel.

Troisième situation

• Considérons maintenant le cas réel d’une planète qui tourne autour du Soleil et sur elle-même. Les deux mouvements vont se combiner pour donner le mouvement réel apparent du Soleil dans le ciel. Or le mouvement dû à la rotation de la planète sur elle-même se fait dans le sens rétrograde, alors que celui dû au mouvement orbital se fait dans le sens direct.

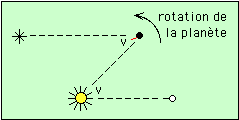
Par rapport à la situation précédente, on remarque que la planète a tourné sur elle-même d’un angle j, ce qui fait que le Soleil ne s’est déplacé dans le ciel que de l’angle v - j.

Conséquences

On voit immédiatement que si la planète tourne sur elle-même à la même vitesse qu’autour du Soleil, on a v = j, donc v - j = 0 ; le Soleil reste toujours à la même place dans le ciel. C’est le cas particulier où les forces de marée ont asservi la planète à tourner dans le même temps sur elle-même et autour du soleil. Ce cas ne se présente pas pour les planètes du système solaire, mais il y a de telles résonnances dans les systèmes de satellites. C’est d’ailleurs le cas de la Lune qui tourne toujours la même face vers la Terre (mais son orbite excentrique complique un peu les choses). Vue de la Lune, la Terre est toujours à peu près au même endroit dans le ciel.

D’autre part, si v > j, alors v - j est positif ; donc le mouvement moyen du Soleil se fera dans le sens direct. Par contre, si v < j, le mouvement apparent du Soleil sera dans le sens rétrograde.

Nous pouvons maintenant calculer la durée du jour solaire en fonction de celles du jour sidéral et de l’année, en supposant l’orbite circulaire.

Formule

Soit :

• v = 2 π t / T, où T est la durée de l’année. L’angle ainsi défini est l’anomalie moyenne. (la planète fait un tour complet, c’est-à-dire 2 π, autour du Soleil en un an = T jours ; donc en 1 jour, elle tourne T fois moins, soit 2 π / T ; et en t jours, t fois plus soit 2 π t / T).
• j = 2 π t / j_s, où j_s est la durée du jour sidéral, et t est mesuré en jours (solaires moyens terrestres).

En remplaçant v et j par les formules ci-dessus, on obtient : v - j = 2 π t / T - 2 π t / j_s

v - j est l’angle apparent dont a tourné le Soleil pendant le temps t. Si S est la durée du jour solaire moyen, v - j = 2 π t / S

Donc : v - j = 2 π t / T - 2 π t / j_s = 2 π t / S

En simplifiant par 2 π t, il vient : 1 / T - 1 / j_s = 1 / S

d’où :

L’inverse du jour solaire s’obtient donc en retranchant l’inverse du jour sidéral à l’inverse de l’année de la planète.

Exemples

Nous allons faire le calcul pour Mercure, Vénus et la Terre. Nous connaissons la durée de l’année et celle du jour sidéral ; nous en déduirons la durée du jour solaire moyen à l’aide de la formule : 1 / S = 1 / T - 1 / j_s.

Mercure :   T = 87,969 j   j_s = 58,6462 j

1 / S = 1 / 87,969 - 1 / 58,6462 = 0,0113676409 - 0,0170514032 = - 0,005683762

S = -175,9398 j

Le signe est négatif, donc le sens apparent du Soleil est rétrograde. Le Soleil se lève à l’est.

Attention ! La formule utilise la vitesse constante d’une planète ayant même durée de l’année mais une orbite circulaire. On peut donc dire que pour Mercure le Soleil se lève à l’est (comme sur Terre), en première approximation. A certains instants, le Soleil peut cependant se déplacer en sens inverse, nous le verrons dans l’animation présentée plus bas.

Remarquez de plus que 3 × 58,6462 = 2 × 87,969 = 175,938.

D’où la relation : 3 js = 2 T = - S

Sur Mercure, 1 jour solaire = 2 ans = 3 jours sidéraux (au signe près).

Cette contrainte a été imposée par les forces de marée produites par le Soleil sur la jeune planète encore chaude. Des calculs ont été faits pour déterminer le temps nécessaire au développement de la contrainte : il apparaît que ce temps est de l’ordre du milliard d’années, si Mercure tournait sur elle-même rapidement au départ, en 8 heures seulement. Mais ce calcul, qui montre que ce que nous observons est possible ( ! ), a un autre intérêt, il permet de calculer la chaleur dégagée par ces marées. Elle est très importante, puisque la température de Mercure a été augmentée de 100 ℃ par les frottements produits. Ce résultat est à rapprocher des effets de marée actuels qui se produisent sur Io, satellite de Jupiter.

Vénus :   T = 224,7 j   j_s = -243 j

T / j_s = 224,7 / -243 = 0,924691358 n’est pas un rapport simple. Il n’y a pas d’asservissement par les marées comme sur Mercure.

1 / S = 1 / 224,7 - 1 / ( - 243) = 0,004450378 + 0,004115226337 = 0,0085656049.

S = + 116,75 j

Sur Vénus, le signe est positif, donc le sens est direct, et le Soleil se lève à l’ouest.

Malheureusement, les nuages qui couvrent Vénus en permanence empêchent de le voir ! De toutes façons, étant données les conditions infernales qui règnent sur Vénus, qui souhaiterait y contempler un coucher de Soleil ?

La Terre :   T = 365,2422 j   j_s = 23 h 56 mn = 1.436 mn = 0,9972 j.

1 / S = 1 / 365,2422 - 1 / 0,9972 = 0,0027379 - 1,00280786 = - 1,0000699.

S = - 1,0000699 j

On retrouve donc que le jour solaire moyen sur Terre est égal à 1… jour solaire moyen terrestre !

De plus, le signe - indique une rotation rétrograde, donc le Soleil se lève à l’est…

C’est toujours encourageant de vérifier que les formules obtenues donnent bien le résultat attendu !

Variations de vitesse

La majorité des planètes du système solaire ont des orbites très proches de cercles. Mais Mercure, Mars et Pluton font exception, avec des excentricités notables. Il s’ensuit des variations de vitesse importantes entre le périhélie et l’aphélie. Prenons le cas de Mercure. Nous avons vu, sur les valeurs moyennes, que le jour solaire y était égal à deux années, ou trois jours sidéraux. Prenons maintenant en compte les variations de vitesse.

La vitesse d’une planète sur son orbite est donnée par la formule :

v² = GM (2/r - 1/a)

où r est la distance au Soleil, et a le demi-grand axe de l’orbite. On peut définir les deux cas particuliers correspondant au périhélie et à l’aphélie. Au périhélie, r = a (1 - e) et à l’aphélie r = a (1 + e). En substituant on obtient :

Au périhélie, la vitesse de Mercure sur son orbite est de 58,98 km/s.

  Animation montrant le jour solaire

---=OO=---