Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Topologie de l’Univers | |||||||
Peut-on voir l’espace ? Non ! On voit un objet, situé à une certaine distance. Entre notre œil et l’objet, on ne voit rien. Dans le langage courant, on dit qu’il y a là du vide. Par exemple lorsqu’on se trouve au sommet d’une montagne, et qu’on regarde vers la vallée, ce vide peut donner le vertige. Mais il est facile de constater que ce vide ne l’est pas : il contient de l’air qui devient palpable s’il se met en mouvement.
Le mot espace, dans le langage courant, désigne ce qu’il y a entre un objet et nous par exemple. Il devient nécessaire parce que nous pouvons aller vers l’objet. Ce déplacement prend un certain temps, qui est une façon de percevoir la quantité d’espace qui était située entre l’objet et nous. On peut aussi se déplacer selon une direction perpendiculaire, et l’espace prend alors une seconde dimension. On peut regarder l’oiseau s’envoler, et il en prend une troisième. Tout ceci reste bien flou, et pour fonder la physique, il a fallu aller bien plus loin.
La physique étudie les mouvements, les objets dans leurs relations les uns avec les autres. Pour définir un mouvement, il faut bien dire d’où l’on part et où l’on arrive. Donc, préciser des positions. Par rapport à quoi ? Par rapport à l’espace, qu’on doit mesurer. Notre concept flou doit donc être précisé, en un modèle mathématique qui permettra des mesures et des comparaisons (deux objet qui sont au même point sont en contact). L’histoire prend là toute son importance.
La notion d’espace a tout d’abord été précisée par les Egyptiens, lorsque chaque année ils devaient reconstruire leur cadastre après la crue du Nil. Il leur a fallu développer une méthode pratique pour retrouver les bornes de leurs champs. C’est l’invention de la géométrie (littéralement : mesure de la Terre), avec les mesures de longueur et probablement aussi d’angles. Les Grecs ont ensuite idéalisé ces notions, et ont produit le premier modèle abstrait de la géométrie.
Ce modèle est celui de la géométrie euclidienne. En effet, pratiquement, il est plus facile d’aller tout droit que de suivre une courbe délicate à reproduire. Donc, la géométrie s’est fondée sur l’étude des lignes droites, et des angles qu’elles forment entre elles. Euclide a formalisé cela dans sa Géométrie Euclidienne, définie à l’aide de postulats.
On peut se faire une idée assez juste de la géométrie euclidienne en regardant un sol pavé de carreaux (carrés par définition). Les deux systèmes de lignes perpendiculaires que les carreaux dessinent représentent les repères entiers de positions particulières. Entre deux de ces repères, on interpole. On peut imaginer une troisième dimension en hauteur. Oubliant les carreaux, ne conservons que les lignes, et imaginons-les matérialisées par des fils de fer. Ajoutons aussi la troisième dimension. Ce grillage représente la structure de l’espace euclidien. On peut remarquer que deux lignes côte à côte sont parallèles, et ne se rejoignent jamais si on prolonge le carrelage indéfiniment par la pensée.
Les postulats d’Euclide sont au nombre de 5. Il est remarquable que les 4 premiers n’aient pas posé de problème d’acceptation, mais que le cinquième soit apparu, pour la plupart des géomètres, comme superflu. A tel point qu’ils ont, pendant des siècles, cherché à le démontrer à partir des 4 premiers… sans succès ! Jusqu’à ce que l’on démontre enfin que ce n’était pas possible (1829, Lobatchevski). Ce cinquième postulat est indispensable pour définir la géométrie euclidienne.
Mais alors, que se passerait-il si on n’acceptait pas ce postulat ? Des géomètres se sont posé le problème à la fin du XIXe siècle. Il leur est apparu que, pour construire une géométrie cohérente et complète, il fallait mettre un cinquième postulat. Donc, ils ont modifié le cinquième postulat d’Euclide. Et ils ont obtenu deux familles de géométries distinctes entre elles et distinctes de la géométrie euclidienne : ce sont les géométries elliptique (courbure positive, Riemann 1867) et hyperbolique (courbure négative, Lobatchevski 1829, Bolyai 1832). La géométrie euclidienne est de courbure nulle.
De ce point de vue, l’espace est donc une construction. Il n’a pas encore de réalité physique. Si l’Univers est fini, l’espace existe-t-il au-delà ? Dans la conception euclidienne, la réponse pourrait être affirmative. Mais Einstein a donné une réponse physique à cette question.
Les deux nouvelles géométries ont été considérées comme de belles constructions mathématiques, jusqu’à ce qu’Einstein s’en empare pour fonder la Relativité Générale.
La géométrie est la mesure de l’espace : étant donnés deux points, on veut déterminer par exemple leur distance. La topologie est d’une autre nature. Se référant elle aussi à l’espace, elle ne considère plus les distances, mais seulement les possibilités offertes par la forme de l’espace.
Première idée : imaginez que l’espace soit constitué de deux sphères qui ne se touchent pas. Il sera impossible d’aller de l’une à l’autre. On dit que cet espace n’est pas connexe. Un espace connexe est donc un espace dans lequel on peut joindre tout couple de points (on peut aller de n’importe quel point à n’importe quel autre).
Deuxième idée : puisque les distances, les longueurs, ne sont pas importantes, une boucle est équivalente à une boucle plus petite. Que la boucle soit irrégulière, ou bien soit un cercle parfait, n’a pas davantage d’importante. Et on peut donc rétrécir une boucle indéfiniment, jusqu’à la réduire à un seul point (comme une ficelle avec un nœud coulant qu’on serre). Mais pas toujours ! Prenez une sphère, et dessinez-y une boucle quelconque. Vous pourrez toujours la réduire à un point par contraction. Par contre si l’espace présente un trou, comme par exemple un tore, certaines boucles ne pourront pas se réduire à un point. Par exemple celles qui enserrent le trou du tore. Mais elles pourront toutes se réduire à une même boucle minimale.
Cette notion de réduction à une boucle minimale est importante, c’est elle qui permet de définir deux topologies identiques. Pour bien le comprendre, cherchez l’intru :
88888888o888
Les huit sont formés de deux boucles attachées. Elles présentent un trou, et ne peuvent se réduire à un point. Le o contient un seul trou. Mais on peut dessiner les huit dans toutes les polices immaginables ; si ce sont des huit, on les reconnaîtra à la présence des deux boucles. Attention toutefois, le symbole infini, un huit couché, est bien topologiquement équivalent à un huit. Ce n’est pas pour rien qu’on peut dire huit couché.
La Relativité Générale traite d’un espace a priori connexe, et défini la gravitation comme une déformation géométrique de l’espace-temps. Elle ne prend pas en compte les diverses topologies possibles. Pourtant, ces dernières pourraient avoir un rôle capital dans la perception que nous avons de l’Univers. Dans certaines topologies, une même galaxie pourrait nour donner plusieurs images, d’aspect différent, nous donnant l’illusion d’un nombre apparent de galaxies bien supérieur au nombre réel. L’Univers pourrait aussi nous apparaître plus vaste qu’il n’est en réalité.
Créer des théories mathématiques de l’Univers est bien beau. Mais si ces théories ne peuvent être confrontées avec les observations, elles restent de peu d’intérêt. Or la topologie de l’espace définit des propriétés qui pourront être vérifiées ou infirmées, peut-être pas très rapidement, mais dans un avenir envisageable. Par conséquent, ces théories pourront être soit invalidées, soit justifiées par l’observation.
L’espace nous apparaît-il toujours identique ? On peut le considérer dans différentes directions autour de nous, à différentes distances, à différentes époques, à différentes échelles. Ces points de vue nous montrent-ils toujours le même aspect ?
Nous avons vu plus haut que l’on n’observe pas directement l’espace, mais qu’on déduit ses propriétés de l’observation de son contenu. Or les méthodes de cette observation sont diverses. Elles comprennent l’étude du ciel profond, qui permet d’accéder aux galaxies proches et à l’Univers lointain. Elle inclus aussi la physique de l’infiniment petit, puisque là ce sont les mouvements et les interactions des particules élémentaires qui font l’objet d’études. Les particules sont plongées dans un espace, on mesure leur position et leur vitesse un peu à la manière des mesures en Mécanique Céleste.
On constate tout d’abord, que ce soit en Astronomie ou en Physique Nucléaire, que l’espace est continu, tel qu’on l’imagine. Il est connexe : de tout point on peut aller vers tout autre. Par conséquent, une même représentation théorique doit convenir. Mais il faut retenir une leçon de la Relativité Générale : la gravitation s’exprime comme une déformation de l’espace-temps, et le contenu en matière-énergie est indissociable de l’espace-temps lui-même. Alors, à l’autre bout de l’échelle, dans l’infiniment petit, il n’est pas raisonnable d’ignorer la gravitation pour construire une théorie vraiment pertinente. Toutefois, dans les conditions actuelles (celles de nos laboratoires), la gravité étant 1039 fois plus faible que l’intéraction électromagnétique, il est bien correct de la négliger. Ce n’est plus le cas lorsqu’en cosmologie, on s’intéresse à ce qui s’est passé peu de temps après le Big-Bang. La densité de l’Univers était telle que la gravité était énorme, et il n’est plus question de la négliger. Seulement, à cette échelle, la Mécanique Quantique règne, et la nécessité de réunir ces deux théories en une seule cohérente se fait sentir. Cette théorie n’existe toujours pas à l’heure actuelle.
Lorsqu’on aura réussi à la construire, comment l’espace y sera-t-il décrit ? La Mécanique Quantique nous a appris que l’énergie est quantifiée (non continue). Et puisque l’espace-temps est intimement mêlé à l’énergie, il est fort probable qu’il apparaîtra également quantifié.
Ce que l’on envisage actuellement, c’est un espace-temps microscopique (à des échelles proches de la longueur de Planck), soumis aux relations d’incertitude d’Heisenberg. Sa forme même devrait fluctuer. Et l’image la plus pertinente qu’on puisse donner est celle d’une écume.
L’image de l’espace est un peu analogue à celle de la mer vue d’avion. A très haute altitude, elle apparaît lisse, uniforme, légèrement courbée par la rotondité de la Terre. Plus bas, on distingue des vagues, et bien que sa forme générale soit inchangée, on y voit des fluctuations locales. Enfin, à très courte distance, on voit l’écume, avec des gouttes qui se détachent, puis retombent et s’y réincorporent. Ceci donne une idée de ce que pourrait être l’espace-temps, selon l’échelle à laquelle on l’observe.
Les théories actuelles ne peuvent mêler vraiment Mécanique Quantique et Relativité Générale, pour la raison que la description de l’espace n’est pas la même b;: l’espace est rigide et euclidien pour la première, déformable pour l’autre. Dans ce qui suit, nous verrons la structure de l’espace-temps à grande échelle. Pour traiter de topologie, le mieux est de prendre des exemples.
Premier exemple : un plan infini dans toutes les directions possède une topologie simple. Il est connexe (on peut aller de n’importe quel point à n’importe quel autre), et infini. Si vous tracez une courbe fermée à sa surface, vous pourrez toujours la réduire à un point : la topologie n’a pas de trou.
Deuxième exemple : une feuille de papier. C’est une partie de plan, c’est donc un espace semblable au précédent mais fini. Là encore, toute courbe fermée peut se réduire à un point. Mais la finitude entraîne une différence fondamentale : cet espace topologique possède un bord. Arrivé à ce bord, il n’est pas possible de continuer tout droit, il n’y a plus d’espace au-delà (au-delà étant un mot de notre espace, puisqu’il n’y a rien après le bord de la feuille). Il est tentant d’assimiler la finitude de l’espace à la présence d’un bord. Mais ceci est faux, nous en verrons plusieurs exemples.
Troisième exemple : enroulons la feuille de papier pour en faire un cylindre, et collons les deux bords joints. Nous obtenons une topologie d’espace fini, mais différente de celle de la feuille déroulée. En effet, si vous y tracez une courbe fermée qui fasse le tour du cylindre, il vous sera impossible de la réduire à un point. Cette topologie présente un trou.
Quatrième exemple : le cylindre est un bout de tuyau. Prenons un bout de tuyau en caoutchouc pour des raisons de commodité, et enroulons-le de telle manière à rejoindre les deux extrémités. On forme ainsi un tore. Une boucle autour du tuyau ne peut toujours pas être réduite. Mais une boucle le long du tuyau, qui se rejoint à la liaison entre les deux extrémités, ne peut non plus se réduire. Pour bien comprendre cette notion, entourez donc le tore avec une ficelle, et essayez de tirer pour faire un nœud. Pour cette analogie, on donne le nom de lacet à ce genre de boucle.
Une surface est monoconnexe si tout lacet qui y est dessiné peut être réduit à un point. Dans le cas contraire, la surface est multiconnexe.
Prenons le tore à deux dimensions vu plus haut. Il se construit à partir d’un rectangle. Plaçons dans ce rectangle deux galaxies, l’une, notée O, étant celle de l’observateur, l’autre étant nommée G. Les galaxies rayonnent de la lumière dans tous les sens. Mais un seul rayon part de la galaxie G en direction de la galaxie O. De O, on voit donc une image de G et une seule.
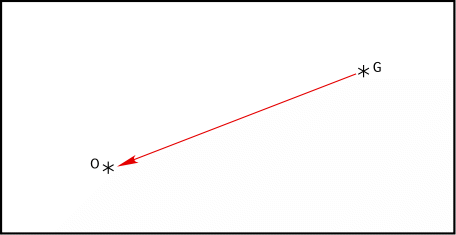
fig. 1
Lorsqu’on enroule la feuille pour produire un cylindre, on identifie ses deux bord opposés. Par collage, chacun des points du bord haut se retrouve identique au point correspondant du bord inférieur (A et B sont réunis en un seul point ; C et D également ; et aussi tout point sur les bords haut et bas, en particulier E et F). Là où on avait un bord, on trouve une continuïté. Par conséquent, un rayon lumineux issu de G qui arrive au bord haut du rectangle, peut continuer sa route à partir du bord bas, bien entendu en ligne droite (puisqu’il y a continuïté au niveau du collage, il n’y a pas de cassure du rayon).
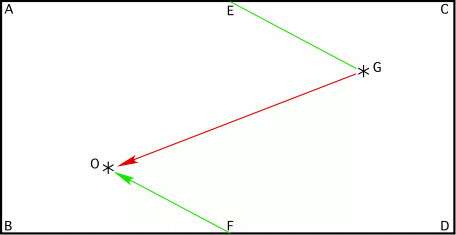
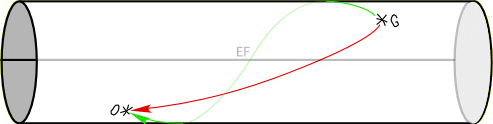
fig. 2
Les deux rayons, rouge et vert, issus de G, arrivent en O (le rouge passe par devant, le vert par derrière). L’observateur voit donc deux images de la galaxie G. Mais ces deux images proviennent de deux directions différentes ! Il aura donc l’impression de voir deux galaxies là où il n’y en a qu’une…
Comment voit-on ces images ?
On voit deux images de la galaxie G, mais sous un angle différent, d’éclats différents, d’âges différents… Il sera bien difficile de prouver qu’il s’agit bien de la même galaxie. Pire encore, nous verrons notre propre galaxie O, telle qu’elle était il y a un certain temps, celui mis par sa lumière pour faire un tour de l’Univers ! Même si c’est un rêve pour un astronome de voir notre Galaxie, il serait bien difficile de la reconnaître…

fig. 3
Ces considérations simples indiquent que l’Univers pourrait être plus complexe que ce qu’on imagine en général ; qu’il serait possible de le prouver, mais que ce sera difficile par identification simple des images.
Quelle est la taille de cet Univers ? On peut dire que la galaxie G est éloignée de O d’une distance correspondant au temps mis par sa lumière pour aller de G à O. Mais puisqu’il y a plusieurs chemins possibles pour cette lumière, il y a aussi plusieurs distances ! Evidemment, on peut considérer la plus courte comme étant représentative. Mais si on regarde G par le rayon vert, on verra une galaxie plus lointaine ! On pourrait en déduire que l’Univers est plus grand qu’il n’est en réalité. Voici pourquoi la topologie de l’Univers, si elle présentait ce genre de propriété, pourrait nous faire croire à un univers plus grand qu’il n’est en réalité, et bien plus peuplé.
Cet univers montrerait-il seulement deux images d’une galaxies ? Non, car la lumière pourrait faire plusieurs fois le tour de l’univers avant de nous parvenir :
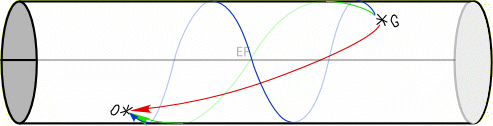
fig. 4
Le rayon bleu fait un tour complet de l’univers avant de parvenir en O. Un autre rayon peut faire deux fois le tour…
Le cylindre, comme la feuille, est un univers fini, mais il possède encore un bord. Pour obtenir le tore, il faut le courber, et abouter ses deux extrémités, ce qui aura pour effet de supprimer le dernier bord. Tous les rayons que nous avons vus sur le cylindre existent aussi sur le tore ; mais il en existe d’autre encore. Il est facile de concevoir que ce sont des rayons qui passeront par une extrémité du cylindre et par l’extrémité qui lui est collée. Ceci multiplie encore les images d’une même galaxie.
La tessellation est une représentation plus commode d’un univers (d’une topologie). Nous l’illustrerons d’abord sur le cylindre. S’il est facile de tracer le rayon direct de G à O, il n’est pas si simple de représenter celui qui franchit un bord de le feuille génératrice du cylindre. En fait, il suffit de dessiner deux copies de l’univers pour trouver ce rayon. Plaçons deux copies identiques l’une au-dessus de l’autre :

fig. 5
Glissons la copie supérieure sur l’inférieure. La partie du rayon vert qui s’y trouve (dans sa partie inférieure) passera dans la partie inférieure du résultat. De même la partie inférieure du rayon bleu (en haut) se retrouvera en bas, pointant vers la galaxie O (fig. 2 en haut). Enroulant le dessin formé de cette superposition, nous obtenons le cylindre, avec les rayons voulus(fig. 2 en bas).
Pour construire le chemin qui fait un tour complet du cylindre, il faut ajouter une troisième copie :
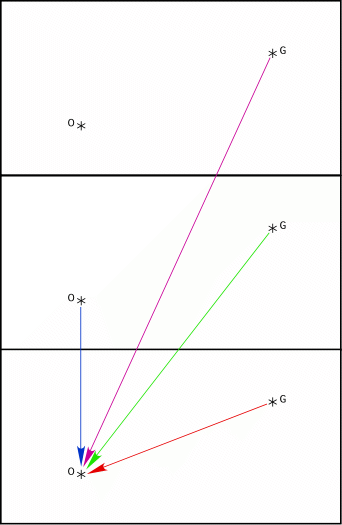
fig. 6
Les bords droit et gauche de ce schéma correspondent aux extrémités du cylindre (l’enroulement se fait selon un axe horizontal). Pour passer du cylindre au tore, il faut identifier ces deux bords. Ce qui revient, en extrapolant la méthode ci-dessus, à reproduire le schéma horizontalement :
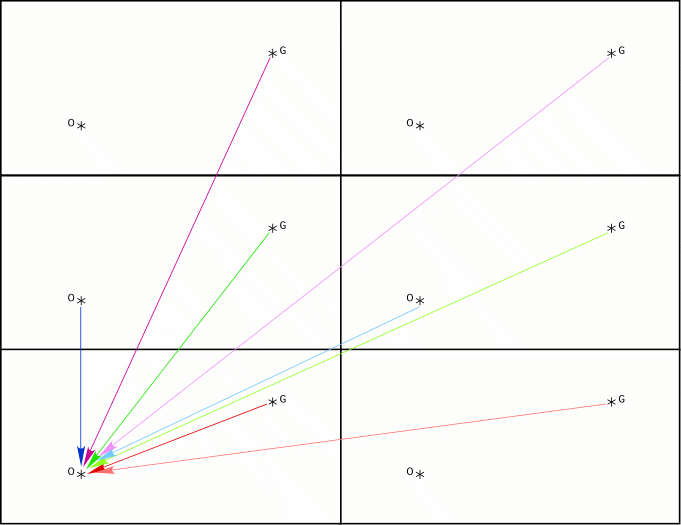
fig. 7
La tessellation correspondant au tore est donc un damier infini, répétition dans les 4 directions d’un motif de base. Le mot tessellation vient de tesselle, qui signifie carreau. Un tel pavage est nommé revêtement universel.
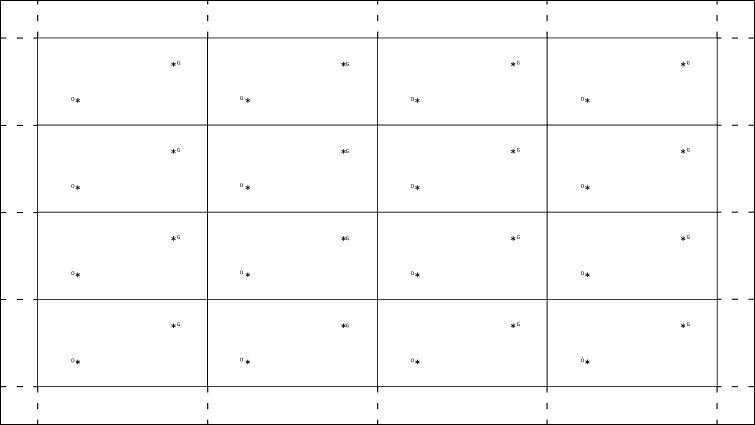
fig. 8
Jusqu’ici, nous avons raisonné sur un univers bi-dimensionnel. Le motif de base est donc un rectangle. Si on passe à trois dimensions, c’est-à-dire à un univers qui ressemble davantage à l’Univers réel, on doit partir d’un parallélépipède. A la place des bords linéaires, on a les 6 faces du parallélépipède. Il faut, de la même manière, associer deux à deux les faces opposées. Le résultat est de même nature que le tore, mais c’est une surface à trois dimensions. On la nomme hypertore. Pour visualiser simplement l’hypertore, il faudrait nous trouver dans un espace à 4 dimensions, ce qui n’est pas le cas. Aussi, la représentation mentale est bien difficile à faire, et la tessellation est-elle d’une grande utilité. Dans chacune des directions, il faut imaginer un pavage infini de motifs identiques. Et les images qui se forment dans un tel univers se conçoivent alors facilement.
Il est surprenant de constater que Karl a décrit, en 1900, un univers hypertorique, dans lequel notre propre galaxie donnerait une infinité d’images. Discutant la découverte de ces images, il montre qu’il serait absurde de penser qu’elles sont de véritables galaxies, toutes identiques, et qu’il serait préférable de penser qu’il s’agit de la même, visible dans un hypertore.
La bande de Möbius est une bande de papier qu’on colle par ses extrémités, après lui avoir fait subir une torsion. Ceci a pour effet d’identifier les coins de la bande en diagonale. Et cette identification change totalement la topologie de la bande puisque, à l’origine, elle possède deux faces et quatre bords, et qu’après elle n’a plus qu’une seule face et un seul bord.

fig. 9
Suivez le bord supérieur de la bande, de A vers B. En arrivnt en B, vous êtes tout aussi bien au point B en bas à gauche, puisque la bande est ainis collée. Suivez maintenant la ligne inférieure, et vous retournez au point A. Vous avez parcouru tout le bord de la bande, de manière continue. La bande n’a bien qu’un seul bord…
Les trois surfaces précédentes sont des topologies multiconnexes (il existe des lacets qui ne se contractent pas en un point), dont la géométrie est euclidienne. Il n’en reste qu’une seule qui est la bouteille de Klein. La bouteille de Klein s’obtient par collage d’une bande, à la manière de Möbius d’un côté, du cylindre de l’autre :
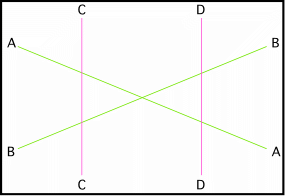
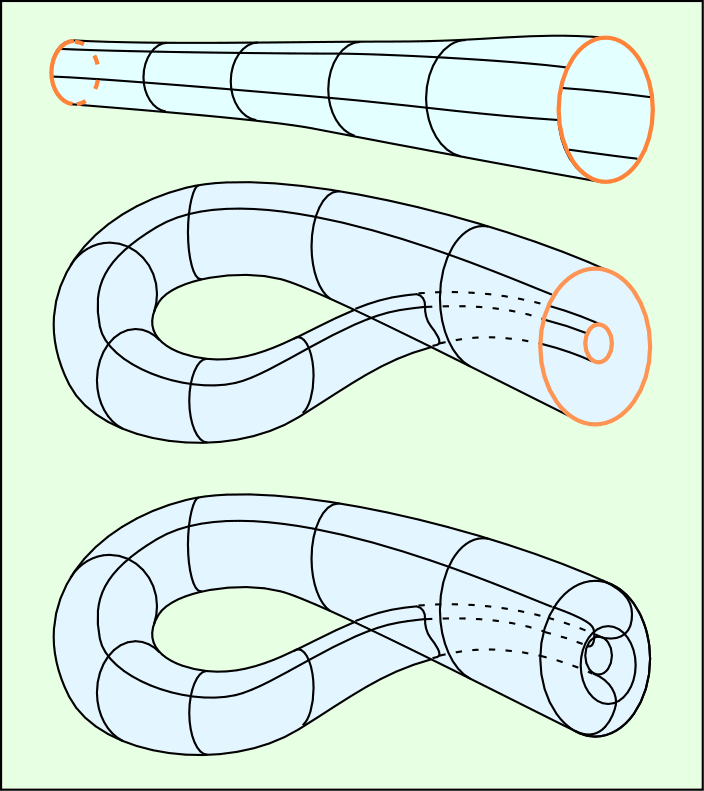
fig. 10
Regardez le premier dessin. Il représente le cylindre (collage des bords CD du carré). Si on enroule normalement ce cylindre, on obtient le tore : avant le collage les deux extrémités du cylindre se font face. Mais au lieu de cela, on replie le cylindre de façon que ses deux extrémités soient orientées dans le même sens. C’est ce qui est produit par le croisement des bords AB. Et puisque les deux extrémités ne se font plus face, il faut bien de replier une pour pouvoir la coller à l’autre.
Ce sont deux notions à ne pas confondre. La géométrie est définie par le Relativité Générale, et c’est une propriété locale. Les équations différentielles qui la définissent permettent de trouver un point infiniment voisin d’un point donné. Connaissant un point, et les courbures en ce point, on peut en effet calculer un point voisin. Mais il faudra connaître la courbure en ce nouveau point pour pouvoir aller un peu plus loin. Nous sommes loin d’une connaissance globale de l’Univers dans son ensemble.
Par contre, la topologie s’adresse à la forme globale de l’Univers, ignorant ses propriétés locales.
Nous avons envisagé le tore (topologie) construit à partir d’un cube. Ce tore possède une géométrie euclidienne, car sa courbure est partour nulle. Mais on peut déformer le cuve de base en le gonflant (ses faces deviennent courbes, bombées), et son utilisation pour un pavage donnent un espace elliptique (courbure positive). Alternativement, on peut dégonfler le cube, et provoquer un creusement de ses faces. Leur coubure devient négative, et l’utilisation d’un tel cube dégonflé dans un pavage donne une topologie hyperbolique (à courbure négative).
La connaissance de la géométrie de l’Univers n’implique donc nullement celle de sa topologie. Et les deux sont nécessaires pour définir complètement la structure de l’Univers.
Le tore (ou hypertore) est obtenu à partir d’un carré, et la topologie est fixée par les identifications de points. L’identification consiste à faire correspondre, à un point du bord du motif, un autre point d’un bord opposé. Cette association se nomme holonomie.
Il existe d’autres façons de paver l’univers.
Il ne faut pas confondre espace et espace-temps. Le premier est l’espace tel qu’on le concevait du temps de Newton, totalement indépendant du temps. Le second est le mélange intime de l’espace et du temps tel qu’il ressort de la Relativité (Restreinte et Générale). Toute mesure de l’un dépend de l’autre, et ils sont donc inséparables. Mais les notions de courbure et de topologie s’appliquent à un espace, c’est-à-dire à l’une ou l’autre des deux interprétations précédentes. On peut donc parler de la courbure de l’espace, ou de la courbure de l’espace-temps. La première est une déformation de l’espace indépendante du temps (constante donc). La seconde peut varier au cours des âges.
Les notions de topologie peuvent aussi s’appliquer aux deux formes. Mais la cosmologie étant basée sur la Relativité Générale, c’est normalement à l’espace-temps qu’on les adapte.
Créer des théories mathématiques est une activité en soi, mais leur intérêt astrophysique n’apparaît que si ces théories sont vérifiables observationnellement. C’est donc ce problème qu’il faut maintenant aborder.
Quelles sont les conséquences de la topologie sur les observations ? La topologie est un phénomène global, qui concerne l’Univers dans son entier. Il faut donc se baser sur une observation intégrale, qui couvre la totalité du ciel. L’Univers aujourd’hui est visible dans les galaxies proches qui nous entourent, pour lesquelles on peut négliger le temps de parcours de la lumière. Cet échantillon n’est donc pas représentatif. Si on veut aller plus loin, il faut observer des objets très faibles, avec un temps de prise de vue bien plus long. Et le champ de prise de vue est très faible, donc la couverture totale du ciel n’est pas possible.
La situation semble donc compromise, mais il existe une observation qui soit globale, et qui, à l’inverse des galaxies, nous montre tout le ciel au même moment ! C’est le fond diffus cosmologique. Sa lumière a été émise au moment où l’Univers est devenu transparent, c’est-à-dire lorsque les électrons se sont accrochés aux noyaux atomiques. Ce phénomène dépend de la température, et celle-ci était décroissant avec l’expansion. De ce fait, cette température a été atteinte brusquement (au sens astronomique du terme) et partout. La lumière, qui était piégée dans la matière chargée, s’est d’un coup trouvée libre dans une matière devenue neutre. Cette époque de l’Univers est nommée recombinaison. On peut sélectionner cette lumière, l’isoler de celle qui est produite aujourd’hui, par sa couleur. Au moment où elle a été émise, la température de l’Univers était de 3.000 K. Et l’expansion a refroidi l’Univers depuis. Le taux d’expansion depuis cette époque étant de 1.000, la température a chûté du même facteur, et se trouve maintenant à 3 K. Il suffit donc d’observer à la longueur d’onde correspondante pour voir ce phénomène, isolé du reste de l’évolution de l’Univers.
Considérons la Terre comme point d’observation. Puisque la recombinaison a eu lieu partout au même instant, la lumière qui nous en parvient a mis le même temps pour arriver jusqu’à nous, et donc elle a parcouru la même distance. Par conséquent, nous observons une sphère. C’est ce qu’on appelle la surface de dernière diffusion. Il y a donc une grande homogénéïté dans cette observation.
Imaginons qu’on puisse faire la même observatin depuis une galaxie lointaine. Nous observerions aussi une surface de dernière diffusion, mais ce ne serait pas la même, puisque la perspective serait différente, et que les distance aussi seraient autres. La Terre et cette galaxie, seraient centre de deux sphères de dernière diffusion. Si ces sphères sont assez grandes, elles pourraient se recouper. Deux sphères se coupent selon un cercle. Les deux sphères auraient donc un cercle en commun, et les deux observateurs verraient, sur ce cercle, les mêmes objets au même moment, donc à la même température. En mesurant cette température sur le cercle, en admettant que les observateurs puissent communiquer, ils constateraient que la température est bien partout la même sur leurs cercles, et par conséquent qu’ils observent le même cercle. Ces cercles sont nommés cercles dans le ciel.
Le point un peu délicat est ici. Il est évident que deux observateurs éloignés (beaucoup) ne peuvent absolument pas communiquer à cause du temps de parcours du signal. Mais il faut ici se placer dans l’état d’esprit correct pour un univers multiconnexe. Prenons un tore pour fixer les idées. Nous avons appris qu’un tore peut se représenter par un pavage dans lequel un motif (l’univers réel) se trouve reproduit une infinité de fois. Toujours en raisonnant à deux dimensions, le motif est un carré, et l’univers est un tore. Notre galaxie est reproduite dans chacun des motifs. Faisons un dessin des surfaces de dernière diffusion vues depuis deux copies de la Terre :
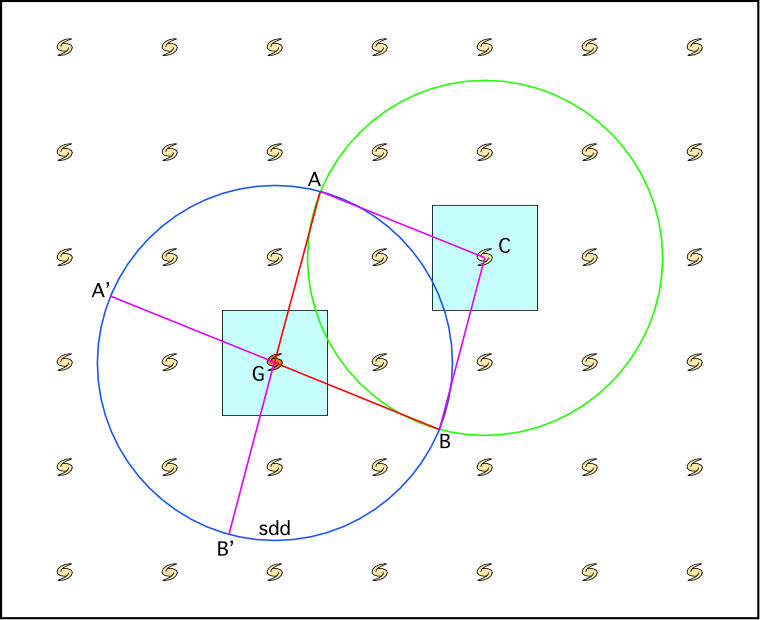
Puisque les deux sphères sont centrée sur deux copies de la Terre, nous verrons l’une vers la droite (sur le schéma), l’autre vers la gauche. Et par conséquent, nous devrons trouver dans le ciel une paire de cercles qui représentent, dans des directions différentes d’observation, une même région de la surface de dernière diffusion (sur le schéma à deux dimensions, les cercles se réduisent aux points A et B, et A’ et B’). Par conséquent, si on trouve deux tels cercles dans le ciel, on aura la preuve que la lumière qui en provient a effectivement parcouru deux trajets différents pour nous parvenir, et donc que l’Univers est multiconnexe. On dispose donc d’un test pour déterminer la topologie de l’Univers.
On peut réfléchir plus profondément sur la taille de la surface de dernière diffusion, par rapport à celle du motif. Et selon le rapport entre les deux, les aspects du fond diffus seront différents. Il contient donc l’information nécessaire pour reconstruire la topologie de l’Univers.
Les premières observations du fond diffus sont celles de COBE. Leur résolution était bien trop faible pour qu’on puisse y trouver des paires de cercles conjugués. En effet, on peut trouver quelle est la taille d’une fluctuation typique de température (germe d’un amas de galaxies futur), et l’on trouve que c’est de l’ordre du degré. Il faut donc des observation qui dépassent cette finesse pour être probantes. Ce n’est pas le cas de COBE, dont la résolution est de l’ordre de 8°.
Ce texte a nécessité de nombreuses sources qu’il est impossible de citer toutes.
Mais l’ouvrage le plus synthétique à consulter est celui de Jean-Pierre Luminet, l’Univers chiffoné.
---=OO=---