Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Cosmologie alternative | |||||||
Le modèle standard de la cosmologie, parfois nommé modèle de concordance, est basé :
Après quelques discussions, le décalage vers le rouge a été interprété comme une vitesse d’éloignement des galaxies lointaines. Cette vitesse proportionnelle à la distance a trouvé une explication toute naturelle, et par là convaincante, dans l’expansion de l’univers. Mais puisque l’Univers est en expansion, en regardant le film à l’envers, on le voit en contraction. Et rien ne vient, a priori, empêcher cette contraction de se poursuivre jusqu’à une singularité, où l’univers devait avoir un volume nul… Cette singularité n’a pas d’explication physique. Mais elle signifie que l’Univers a eu un commencement.
La Cosmologie utilise la Relativité Générale comme base. Or cette dernière modélise l’espace-temps comme une entité maléable, influencée par la matière, et influançant la matière… L’équation simplifiée à l’extrême peut s’écrire G = κ T, où G représente la géométrie de l’Univers, et T son contenu en matière-énergie. κ est une constante de couplage. Cette égalité montre bien que toute variation de G entraîne une variation de T : si la géométrie de l’Univers varie, la matière se déplace. Et à l’inverse, une variation de T entraîne aussi une variation de G : si la matière se déplace, la géométrie change. L’essentiel de la difficulté vient de ce couplage.
Les équations de la Relativité Générale ne sont pas suffisantes pour résoudre le problème. Il faut leur ajouter une fonction donnant la distance entre deux points voisins, fonction nommée métrique.
Le problème est maintenant de déterminer une métrique, et là, les choses se gâtent. La difficulté est trop grande pour pouvoir aborder le problème dans toute sa généralité. Il faut donc simplifier les données pour le rendre gérable.
Un modèle est une solution des équations de la RG, définie par une métrique. Les solutions envisageables sont :
La simplification envisagée par Friedman et Lemaître dès les années 1920 est basée sur le Principe Cosmologique. Celui-ci suppose que l’Univers est homogène et isotrope. L’homogénéité indique que les propriétés qui nous intéressent ont la même valeur partout (en particulier la densité). L’isotropie prétend que ces propriétés sont identiques dans toutes les directions de l’espace. Il n’y a donc pas de direction privilégiée.
L’observation du ciel montre immédiatement qu’il contient des étoiles séparées par de grands vides. Les étoiles se groupent en galaxies, séparées par de grands vides aussi. Les galaxies se regroupent en amas… les amas se groupent enfin en superamas. Au niveau des superamas, on découvre également des vides immenses. Cette image de l’Univers est donc tout, sauf homogène ! Mais on suppose, on pose comme principe, qu’à une échelle encore plus grande (plusieurs centaines de millions d’années lumière), l’Univers est enfin homogène.
Il est évident que cette affirmation est gratuite. En 1920 on n’avait encore aucune idée de ces structures à grande échelle. Et aujourd’hui les observations viendraient plutôt l’infirmer. Mais en posant cette homogénéïté, on obtient un problème intégrable, ce qui est une très bonne justification pour attaquer le problème.
Mais peut-être serait-il sage de reconsidérer ces limitations presque un siècle plus tard…
La famille de ces modèles dépend d’un paramètre : la densité moyenne ρ de l’Univers. Il s’agit de la moyenne, mais d’après le Principe Cosmologique qui sous-tend ces modèles, elle est la même en tout point de l’Univers. Elle fixe les caractéristiques des modèles car ceux-ci sont instables, ils sont en contraction ou en expansion mais ne peuvent être statiques. Pour s’accorder aux observations, c’est l’expansion qui doit être choisie.
L’univers étant en expansion, la gravité mutuelle de toutes les particules qui le remplissent tend à les rapprocher, donc à freiner l’expansion. En effet, le freinage des particules modifie leur position dans l’espace-temps, et donc la géométrie de celui-ci. On s’attend alors à ce que l’expansion soit décélérée. Et aussi que cette décélération soit d’autant plus forte que la densité de l’Univers est plus élevée.
Selon leur densité ρ, les modèles de Friedman-Lemaître se divisent en trois catégories :
Dans les trois cas, l’expansion est freinée.
Les modèles de Friedman-Lemaître sont issus du Principe Cosmologique appliqué à la Relativité Générale. Après une phase de calcul initial indiquant leurs propriétés générales, on est passé à une analyse plus fine, qui a mis rapidement en lumière bien des difficultés.
Première difficulté : la synthèse des éléments légers. Les modèles de Friedman-Lemaître présentent une singularité, donc un commencement. Par conséquent, le contenu de l’univers a eu aussi un début. On sait que la matière primordiale (celle qui n’a pas été transformée par les étoiles) a une composition bien précise, comprenant approximativement 3/4 d’hydrogène, presque 1/4 d’hélium, et une pincée de lithium.
Mais en remontant le temps, la matière est de plus en plus chaude, et l’énergie détruit les atomes, les noyaux, et même les particules… Très peu de temps après le Big Bang, l’Univers était rempli seulement de particules indépendantes, neutrons, protons et électrons. l’Univers se refroidissant par l’expansion, une brève période a permi la synthèse de l’hélium à partir de l’hydrogène : il fallait que la température soit encore suffisante pour vaincre la barrière électrostatique des protons, mais plus trop haute sans quoi les noyaux complexes formés étaient immédiatement détruits. La masse de l’Univers, qui freine l’expansion, détermine la durée de cette période, et donc la quantité d’hélium primordial. La mesure de cette quantité d’hélium indique donc combien de temps cette phase a duré, et par conséquent l’efficacité du freinage. On en a déduit la densité de l’Univers, et trouvé qu’elle doit être de l’ordre de la densité critique : ρnucl ≅ ρc. Cette détermination de la densité moyenne de l’Univers ne dépend que de la composition chimique du gaz.
Il y a bien sûr une méthode plus directe pour mesurer cette densité. Dans une galaxie, la masse et la luminosité globales sont reliées par la relation : M = 4 L (M en masses solaires et L en luminosités solaires). Il s’agit d’une moyenne qui intègre tous les types d’étoiles avec leur luminosité propre, en tenant compte des proportions de chaque type. En observant la luminosité d’une galaxie, on en déduit sa masse. Et de là on peut déterminer la densité de l’Univers : on trouve une valeur de l’ordre de ρvis = ρc / 10. Il y a là un léger problème : cette estimation est dix fois plus faible que la précédente !
Pour pallier à ce problème, le modèle standard de Big Bang incorpore la matière noire, qui est en masse neuf fois plus importante que la matière connue. Avec ces 10 % de matière normale + 90 % de matière noire, on arrive à concilier une gravité expliquant la dynamique de l’Univers, et une nucléosynthèse juste assez longue pour donner les produits attendus. Le seul inconvénient est qu’on n’a jamais vu la couleur de la matière noire… Gardons tout de même à l’esprit que cette absence est peut être provisoire, les recherches continuant en particulier au LHC.
Malgré cette difficulté, l’explication de cette nucléosynthèse primordiale est considérée comme l’un des piliers du modèle du Big Bang.
Seconde difficulté : La platitude de l’Univers. L’Univers nous semble aujourd’hui bien plat. Plat signifie que sa courbure est pratiquement nulle. La courbure est produite par la matière. On pourrait s’attendre à ce que l’univers présente une courbure, positive ou négative, la courbure nulle n’étant qu’une valeur particulière parmi une infinité de valeurs envisageables. Pourquoi l’univers est-il plat ? Ce ne peut être l’effet du hasard, et il faut absolument trouver un mécanisme qui le justifie.
Troisième difficulté : Le rayonnement micro-onde, ou fond diffus cosmologique. Après le Big Bang, l’expansion a fait baisser sans cesse la densité moyenne de l’Univers. Très chaud, celui-ci rayonnait énormément, mais l’énergie rayonnée était immédiatement absorbée par la matière très dense… Jusqu’au jour où cette densité est passé en-dessous d’une valeur critique, rendant l’Univers transparent. Dès lors, les rayonnements ont pu se propager librement, et traverser des étendues immenses pour parvenir jusqu’à nous aujourd’hui. Avec l’expansion, les longueurs d’onde se sont étendues comme l’espace, mille fois, et des rayonnements émis à 3.000 K nous parviennent maintenant à 3 K seulement (l’énergie d’un rayonnement est E = h ν = h c / λ si λ a été multipliée par mille, E et la température qu’elle représente ont été divisées par mille). Il s’agit donc d’un rayonnement micro-onde.
Mais plus on améliore les instruments d’observation, plus ce rayonnement nous apparaît uniforme sur le ciel. Il montre un spectre de corps noir très pur, et une température incroyablement uniforme. Ses valeurs sont identiques sur tout le ciel, au cent millième près… Comment tout l’Univers observable a-t-il pu égaliser ses température à ce point ? Ceci en sachant que la vitesse d’expansion étant plus faible que la vitesse de la lumière, des points éloignés de l’Univers n’ont pas pu communiquer dans les premiers instants ? Ce problème reste ouvert.
L’équilibre thermique de l’Univers ne peut être atteint que par échange d’énergie d’un point à un autre. Pour cela, il faut que l’énergie ait eu le temps de franchir la distance entre ces deux points. Or il est impossible que ce soit le cas dans les premiers instants de l’Univers, dans le cadre du Big Bang simple. Pour provoquer cette uniformisation, on a dû ajouter le paradigme de l’inflation, qui n’est là que pour ça. Et encore faut-il que cette inflation ait des propriétés bien précises, difficiles à admettre. L’alternative est de penser que l’Univers s’est formé dans le Big Bang à température uniforme, mais alors, on ne sait absolument pas pourquoi…
La dynamique des galaxies (étoiles périphériques), et des amas, ne s’explique pas si on considère la matière visible. Ces objets seraient instables. Qu’à cela ne tienne, on a inventé la matière noire pour y remédier : elle est là pour tout stabiliser. C’est la même que celle qui explique la nucléosynthèse, du moins on l’espère !
Quatrième difficulté : cerise sur le gâteau, on s’est aperçu en 1998, en observant des supernovæ de type Ia lointaines, que l’expansion de l’Univers n’est pas ralentie comme on le pensait, mais accélérée. Qu’importe, on ajoute la QSP (quantité suffisante pour) d’énergie noire, et le tour est joué. Evidemment, nous n’avons pas la moindre preuve de son existence.
Comme on le voit, le modèle standard dérive d’une idée simple, l’utilisation de la Relativité Générale, mais sa conception incorpore plusieurs éléments ajoutés pour la circonstance. Pour rendre le problème abordable, on impose des principes supposés raisonnables (Principe Cosmologique). Ensuite, à chaque problème, plutôt que de remettre en question le modèle, on lui ajoute un petit quelque chose pour le remettre sur pieds. Un ingrédient que les physiciens sont priés de bien vouloir découvrir dans leurs laboratoires. Sauf que jusqu’à maintenant, ils n’ont rien trouvé…
Attention toutefois ; Ces critiques ne doivent pas faire oublier que l’ensemble ainsi conçu représente vraiment bien les observations, au moins telles qu’elles sont aujourd’hui. Et il reste tout à fait possible que l’on découvre finalement matière et énergie noires. Les théories physique actuelles ne l’interdisent pas, et au contraire elles proposent des pistes pour les expliquer. La théorie peut le prévoir, mais les observations, les expériences, n’ont jamais rien vu jusqu’à aujourd’hui. Or sans observations pour vérifier, les théories n’ont pas de valeur…
On peut envisager des modèles alternatifs, ce que nous allons faire, mais actuellement aucun d’entre eux n’est à même de tout expliquer. Il faut dire qu’ils ont été infiniment moins travaillés que le modèle standard. Chacun est l’œuvre d’un petit nombre de chercheurs, et depuis un temps bien moindre. Alors, ça vaut la peine de passer en revue quelques-uns de ces modèles, au moins dans leurs grandes lignes. D’ici quelques années, certains auront été complètement écartés, parce qu’on aura trouvé des difficultés majeures (à moins qu’on n’y mette quelque rustine…). D’autres seront plus avancés qu’aujourd’hui, et resteront en course. L’avenir nous le dira.
L’inflation explique l’homogénéité et l’isotropie de l’Univers, parce qu’il aurait eu le temps de s’uniformiser avant elle. Elle explique aussi la platitude : plus une sphère est grande, plus elle paraît plate.
Mais un modèle autre, basé sur une évolution différente, les explique aussi. Il suppose que l’Univers existait avant son expansion, mais qu’il était en contraction. Il aurait poursuivi cette contraction assez longtemps pour s’uniformiser, puis aurait inversé cette évolution. L’arrêt de la contraction se serait produit lorsque les dimensions auraient atteint la dimension de Planck (au temps de Planck). C’est extraordinairement petit, mais stricto sensu la singularité du Big Bang est évitée. Dans sa contraction, l’Univers aurait bien eu le temps aussi de s’aplatir, et ce problème-là est également évité.
Notez bien que le rebond, atteignant le temps de Planck, se produit dans un état physique totalement hors de portée de nos théories actuelles. Cet aspect du modèle le ramène, à ce point de vue, au même point que le Big Bang : il n’explique rien de mieux.
Pour le rendre valide, il faudrait aussi expliquer que la contaction antérieure s’arrête, puis s’inverse en expansion. Mais nous n’avons pas de pistes pour cela.
Une idée semble-t-il plus prometteuse ne remet pas en cause les grandes lignes du modèle standard, mais opère une analyse plus fine des principes de base. Plus particulièrement du Principe Cosmologique qui, comme nous l’avons vu plus haut, est une approximation très grossière à petite échelle, et qui ne prend sens qu’à des échelles de l’ordre de plusieurs centaines de méga parsecs.
Dans ces conditions, comment les amas de galaxies auraient-il pu se former, sans modifier la géométrie de l’Univers ? Leur masse est tout de même loin d’être négligeable. Un modèle réaliste devrait bien sûr prendre en compte cette structuration de l’Univers. C’est justement ce que nie le Principe Cosmologique.
Que pourrait-on dire si on partait d’un principe plus réaliste, en remettant en cause l’hypothèse d’isotropie et/ou d’homogénéité de l’Univers ?
Plusieurs chercheurs se sont penchés sur ce problème, sachant que l’abandon de ces hypothèses complique passablement les équations, au risque de rendre les difficultés mathématiques insurmontables. Considérons d’abord l’isotropie.
Si l’Univers est isotrope, la métrique contient un facteur d’échelle R(t), qui ne dépend pas des coordonnées d’espace. Le facteur d’échelle est le coefficient, variable au cours du temps, qui multiplie les distances entre deux points quelconques. Si à l’instant t0 la distance entre deux points est d, à l’instant t elle sera d × R(t). Le modèle de Big Bang utilise un tel facteur d’échelle.
Si l’Univers est anisotrope, il n’a pas les mêmes propriétés dans toutes les directions. L’allongement des distances selon la direction x n’est pas le même que selon la direction y. Alors, le facteur qui multiplie ces allongements doit être différent, c’est-à-dire que R(t) est remplaçé par trois facteurs : Rx(t), Ry(t), Rz(t). On peut imaginer, en deux dimensions, un tissus élastique que l’on allongerait plus dans une direction que dans l’autre.

Rx(t) = 1,01, Ry(t) = 0,99
Il est évident que ceci complique les équations qui en dépendent, et rend bien plus difficile la recherche de solutions. Il n’est donc pas étonnant que les premiers chercheurs se soient abstenus d’envisager ce cas.
Formellement, c’est la métrique qui est modifiée. La métrique est la fonction qui donne la distance infinitésimale entre deux points voisins. Dans le cas anisotrope, il n’y a pas qu’une seule métrique possible, il y en a neuf. Elles ont été étudiées par Luigi Bianchi, qui leur a donné son nom, en 1897. Etudiées avant la Relativité Générale, ces métriques n’avaient alors qu’un caractère purement mathématique. Elles ont pris ensuite un caractère physique, mais toutes n’ont pas la même valeur de ce point de vue. De plus, les difficultés de résolution ne sont pas de même niveau, et là encore, ce sont les plus accessibles qui ont été les plus étudiées.
On fait déjà un tri en considérant que l’Univers actuel est tout de même assez isotrope. Aussi les métriques retenues sont celles qui tendent vers un espace-temps isotrope. La question importante, pour laquelle Alexandre Friedman s’est intéressé aux métriques de Bianchi, est "ces modèles présentent-ils des singularités ?" Il se trouve que oui. Mais ces singularités sont plus diverses que celle dérivée du Big Bang.
Selon la métrique choisie, on constate que l’espace-temps peut être en contraction selon une dimension, et en dilatation selon les deux autres… Et de plus, ces dimensions peuvent s’échanger. Bref, si on se rapproche de la singularité, on obtient des oscillations qui empêchent de déterminer vraiment ce qu’il se passe. Dans certains cas, on observe même un comportement chaotique.
Vers la singularité, il arrive qu’une dimension s’effondre et tende vers 0, alors que les autres conservent des valeurs finies. C’est une singularité en forme de crêpe. Une autre métrique donne une singularité unidimensionnelle. Ces métriques présentent donc beaucoup de possibilités, qui demanderaient à être confrontées à l’expérience. Mais les difficultés ont freiné jusqu’à maintenant des études précises, et elles restent donc à l’état d’ébauches.
Voyons maintenant ce que donne l’abandon de l’homogénéité. La complexité des équations est bien grande, car les métriques non homogènes sont les plus générales possibles. Les facteurs d’échelle sont maintenant fonction du lieu.
Remarquez à quel point ceci est naturel, même si on le ressent pas a priori. Imaginez l’Univers, avec une galaxie dedans. Il n’y a pratiquement pas de matière partout, sauf où se trouve la galaxie. Il est bien évident que si cet Univers est en expansion, celle-ci sera freinée par la masse de la galaxie là où elle se trouve, et de moins en moins à mesure qu’on s’en éloigne ! Imaginer que l’expansion serait partout pareille est au contraire bien absurde ! Les facteurs d’échelle seront donc de moins en moins perturbés par la masse lorsqu’on s’en éloigne. Ils doivent donc varier selon la position considérée dans l’espace : Rx(x, y, z, t), Ry(x, y, z, t), Rz(x, y, z, t).
Ces métriques présentent une symétrie sphérique : elles possèdent un centre. Il semble donc évident qu’elles ne puissent s’appliquer à l’Univers, sans remttre en cause le Principe Copernicien : la Terre n’est pas au centre de l’Univers ! Pourtant, ces métriques jouent un rôle important en ce qu’elles permettent d’approcher un problème, même si les conditions ne sont pas réalistes.
Ces métriques changent en fonction de la distance à la Terre, ce qui est correct pour prendre en compte les variations locales de l’espace-temps, mais elles changent de la même manière dans toutes les directions : c’est cela qui leur donne la symétrie sphérique, et qui est en désaccord avec ce que nous pensons profondément de l’Univers. Mais si on s’intéresse justement aux phénomènes liés à l’éloignent, elles peuvent nous donner des indications.
La symétrie sphérique se conçoit en imaginant que l’Univers ainsi décrit serait formé de coquilles concentriques à la Terre, ayant chacune ses propres propriétés physiques : densité de matière, température… Considérons un axe issu de la Terre, et une petite zone conique autour de lui. Cette zone est caratérisée par sa densité (celle de la coquille à laquelle elle appartient), qui varie selon la distance à la Terre. On peut penser à une zone semblable contiguë à la première, mais décrite par un autre modèle de même nature, avec simplement une loi de densité différente. Ainsi, on peut concevoir que l’Univers soit découpé en zones coniques centrées sur la Terre, chacune étant décrite par un modèle semblable, mais avec une loi de densité différente.
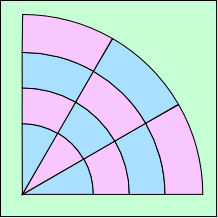
Représentation d’un modèle composite
Les couleurs correspondent à deux densités différentes
Ceci ne constituera pas un vrai modèle parce qu’il n’y a pas de continuité d’une zone à l’autre. Il ne nous apprendra rien sur le passage d’une zone à l’autre. Mais radialement, il prend un certain sens.
En utilisant ces métriques, Marie-Noëlle Célérier a pu obtenir une relation entre la luminosité d’un objet et son décalage vers le rouge. Ceci nous rappelle un vieux souvenir : la loi de Hubble ! On obtient donc une nouvelle loi semblable, mais cependant différente.
Utilisant cette loi, Marie-Noëlle Célérier a montré que l’observation des SNIa peut s’expliquer tout naturellement sans faire intervenir la moindre énergie noire !
En fait, l’accélération de l’expansion serait un artéfact, une conclusion fautive basée sur un modèle trop simpliste. Il ne serait plus nécessaire non plus de réintroduire la Constante Cosmologique. Celle-ci est en effet la traduction mathématique d’une grande variété de phénomènes physiques envisageables : l’énergie noire en est un.
C’est là l’intérêt de ces modèles, qui ne sont pas réalistes certes, mais qui, abandonnant le simplificateur Principe Cosmologique, non validé par les observations, ouvrent des horizons nouveaux à l’étude de la Cosmologie. Un vrai modèle admissible est encore loin, il y a un très important travail mathématique à faire pour cela ; mais la voie semble tracée pour une nouvelle approche dont les fondements sont plus réalistes qu’avant.
Thomas Buchert a envisagé une autre façon de réintroduire des inhomogénéités dans un modèle. Partant de la constation que la méthode traditionnelle gommait toutes les irrégularités de l’Univers en prenant la densité moyenne de matière, identique partout, il a supposé que l’Univers était homogène et isotrope en moyenne. Ce qui est une façon de raccorder le Principe Cosmologique applicable aux grandes échelles (qu’il obtient donc par la moyenne), avec les inhomogénéités évidentes aux petites échelles.
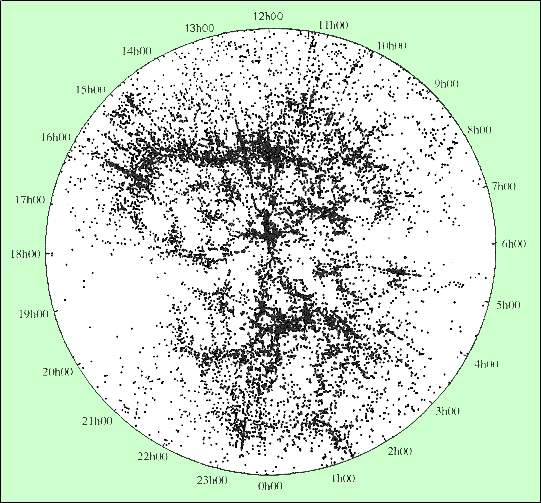
Le Grand Mur est une immense structure qui regroupe des amas de galaxies. Certaines de ces structures s’étendent sur une distance de plus d’un milliard d’années-lumière. Les vides sont de même importance. L’Univers prend donc une forme en nid d’abeille, ou en mousse de savon. Mais en-dessous du milliard d’années lumière, il est loin d’être homogène. La prise en compte de ces immenses inhomogénéités semble bien incontournable !
Si vous mélangez de l’eau chaude et de l’eau froide, il est bien évident que la température moyenne que vous obtiendrez dépend des proportions d’eau chaude et d’eau froide. De la même manière, l’expansion moyenne de l’Univers dépend de la taille des différentes zones contributrices. Considérons deux zones, l’une de faible densité et l’autre de forte densité. L’expansion les emporte toutes deux de la même façon, mais elle est libre dans la zone de faible densité, et ralentie dans l’autre. On peut admettre que la zone dense verra son expansion s’annuler, puis s’inverser en contraction, pour former un amas de galaxies. Sa taille diminue alors beaucoup. Et de ce fait, sa contribution à l’expansion moyenne aussi ! L’expansion forte qui continue dans l’autre zone l’emporte largement dans la moyenne, qui de ce fait peut augmenter. On constate alors une accélération de l’expansion moyenne, alors que l’expansion est décélérée dans toutes les zones…
Cette remarque a été formulée par Syksy Räsänen à partir du modèle proposé par Thomas Buchert. Comme dans le modèle de Marie-Noëlle Célérier, on arrive à la conclusion que l’accélération de l’expansion, déduite de l’observation des supernovæ, pourrait n’être qu’un leurre, conséquence d’un modèle inadapté à la réalité.
Précisons bien ici que l’observation des supernovæ ne donne pas une mesure de la vitesse d’expansion !
Elle ne donne que la magnitude apparente des objets, et leur décalage spectral. On déduit une accélération en évaluant leur distance d’après le décalage spectral, en utilisant le loi de Hubble. L’accélération repose donc, non seulement sur l’observation, mais tout autant sur l’utilisation du modèle standard de Big Bang. Si par hasard celui-ci n’était pas parfaitement exact, l’accélération de l’expansion n’aurait plus de base…
Encore une fois, il est bien trop tôt pour en déduire que le modèle standard est faux. Mais ces travaux illustrent le fait que la Cosmologie en est encore à ses débuts. Elle est très loin d’être achevée, et nos connaissances sur l’Univers doivent être encore considérablement approfondies.
L’équation d’Einstein de la gravité est la base : G = κ T, où G représente la géométrie de l’espace-temps, et T son contenu en matière-énergie.
| Univers vide de de Sitter | T = 0 | ρ = 0 |
| modèles de Friedman-Lemaître | T = constante | ρ = ρ(t) |
| modèle général | T quelconque | ρ = ρ(x, y, z, t) |
Les modèles de Friedman-Lemaître se divisent en trois catégories :
Dans une galaxie, il existe une relation entre la masse globale des étoiles et leur luminosité globale : M = 4 L, les deux valeurs exprimées en unités solaire (masse solaire et luminosité solaire). Cette relation permet de déterminer la masse d’une galaxie en observant sa luminosité. On en déduit que la densité moyenne de l’Univers doit être de l’ordre de ρvis = ρc / 10.
Très peu de temps après le Big Bang, l’Univers se refroidissant par l’expansion, une brève période a permi la synthèse de l’hélium à partir de l’hydrogène. La masse de l’Univers, qui freine l’expansion, détermine la durée de cette période, et donc la quantité d’hélium primordial. La mesure de cet hélium indique que la densité moyenne de l’Univers doit être de l’ordre de la densité critique : ρvis = ρc
Ces deux démarches différentes amènent à deux valeurs contradictoires de la densité de l’Univers. Plutôt que de remettre en question tout le modèle, les cosmologistes ont inventé la matière noire, qui représente la différence. L’Univers contiendrait donc dix fois plus de matière noire (jamais observée) que de matière ordinaire. Pour cela, il faut bien entendu que la matière noire ne participe pas aux réactions nucléaires, et ne soit pas visible. Elle est donc très différente de la matière ordinaire.
Une supernova de type Ia est l’explosion d’une naine blanche qui accrète de la matière, et dépasse ainsi la masse de Chandraskhar. Elle explose au moment où elle dépasse cette limite, et donc toutes les SNIa explosent dans les mêmes conditions. Aussi ont-elles toutes les même propriétés. Des supernovæ Ia lointaines ont été observées. De leur décalage spectral, on déduit leur distance par la loi de Hubble. Connaissant la distance, on déduit la magnitude absolue de la magnitude apparente. Or la magnitude absolue ainsi calculée ne correspond pas à la valeur attendue. On a remis en cause la distance déduite de la loi de Hubble, mais non la loi de Hubble elle-même ! En imaginant que la constante de Hubble soit en fait variable dans le temps, on déduit que l’expansion est accélérée.
Enfin, l’observation du fond cosmologique montre que 380.000 ans après le Big Bang, l’Univers était très homogène, au cent millième près. Or l’expansion est bien trop lente pour que l’Univers ait eu le temps de s’uniformiser ainsi depuis le Big Bang. Pour pallier à cette difficulté, on a imaginé l’inflation : pendant un temps très bref (10-35 secondes) l’expansion a été exponentielle. Ceci permet de comprendre que l’Univers observable aujourd’hui ait été assez petit à l’origine pour s’uniformiser.
De ces considérations, nous déduisons le tableau suivant :
| RG + principe cosmologique => modèles de Friedman-Lemaître (MFL) | MFL + nucléosynthèse primordiale => matière noire | MFL + SN Ia => accélération de l’expansion => énergie noire | MFL + fond cosmologique => inflation |
---=OO=---