Historique de Marseille
| liens |
le 27/09/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 27/09/17 |
||||
| �� Rappels mathématiques | |||||||
Ce chapitre contient des explications simples sur quelques point mathématiques, utiles pour comprendre les formules physiques, et certains points un peu délicats. Ce n’est pas un vrai cours de maths, mais plutôt un guide pour vous aider pas-à-pas si vous en ressentez le besoin.
Les puissances interviennent partout en maths et en physique. C’est une notion très simple, juste basée sur la répétition d’une multiplication. Les explications ci-dessous visent à détailler le calcul sur les puissances, et montrer que leur usage est très naturel. Si vous les trouvez simplistes, c’est parfait !
Par définition, la puissance n est le produit de n termes égaux ; c’est donc une abbréviation :
102 = 10 × 10
103 = 10 × 10 × 10
104 = 10 × 10 × 10 × 10
etc.
Les puissances ci-dessus se lisent "10 puissance 2", "10 puissance 3" et "10 puissance 4".
Nous nous sommes limités à la puissance 4, mais on peut continuer aussi loin qu’on veut :
10n = 10 × 10 × … 10 produit de n termes
(lire "10 puissance n")
Il est bien évident que l’on peut remplacer 10 par 2, ou 3, pour décrire les puissances respectives de ces nombres. De manière un peu plus abstraite, on peut donc remplacer 10 par une lettre, qui est censée représenter n’importe quelle valeur entière :
avec n ≥ 2, n entier, puisque nous sommes partis du carré, qui met en jeu deux termes.
On voit immédiatement que a3 = a2 × a
A gauche du =, il y a trois a et à droite il y en a 2 multipliés par un troisième, donc 3 termes aussi.
Pareillement, a4 = a3 × a (4 termes a de chaque côté)
Et de manière générale, pour toute valeur de n (entière, supérieure ou égale à 2) :
an = an - 1 × a
En fait, la formule ci-dessus est une nouvelle façon, plus correcte, de définir les puissances entières. C’est ce qu’on appelle "définition récursive", en ce sens que pour définir la puissance n, il faut déjà connaître la puissance n - 1. C’est donc un procédé de descente, qui doit être limité. Pour l’instant, on dira donc que la formule est valable pour n > 2 (on se base sur la première puissance définie à ce stade).
Par exemple, a4 = a3 × a. On calcule donc d’abord a3 par le même procédé :
a3 = a2 × a. On est arrivé à a2, qu’on a défini comme a × a. On prend cette définition, et on arrête la descente.
En reportant cette valeur, on a successivement : a3 = (a × a) × a
et a4 = a3 × a = ((a × a) × a) × a
L’associativité du produit (on peut enlever les parenthèses), donne le résultat.
Cette méthode de représentation des problèmes est extrêmement puissante, et constitue la base de résolution des problèmes en Intelligence Artificielle. D’ailleurs, l’intelligence naturelle l’utilise souvent aussi… Si vous voulez un exemple, recherchez le jeu des tours de Hanoï !
Nous avons commencé avec des entiers. Mais on peut aussi calculer le carré d’un nombre décimal :
2,52 = 2,5 × 2,5 = 6,25
La définition et la formule ci-dessus sont donc valables si a prend une valeur décimale quelconque.
Le cas particulier où a = 10 est très important. Son emploi est universel en physique, pour des raisons de commodité.
Par exemple, l’unité de longueur est le mètre, qui correspond à une valeur commode pour nous, à notre échelle, mais qui se trouve totalement inadaptée pour décrire les noyaux atomiques, les longeurs d’onde de la lumière ou les distances dans l’univers.
On résoud ce problème de deux manières différentes :
Les unités dérivées se définissent à l’aide de puissances de 10 : le kilomètre vaut 103 mètres ; l’angström vaut 10-10 mètres ;
Il est envisageable de multiplier deux puissances. Qu’obtient-on ? Soit à calculer : 10n × 10p
Par définition, 10n = 10 × 10 × … 10 (produit de n termes), et 10p = 10 × 10 × … 10 (produit de p termes)
Donc 10n × 10p = 10 × 10 × … 10 × 10 × 10 × … 10 le produit de n termes multiplié par le produit de p termes (le signe de multiplication en rouge sépare les termes des deux puissances).
Il y a donc dans ce produit n + p termes.
Pour bien voir ceci, écrivons-le pour 102 × 103 = (10 × 10) × (10 × 10 × 10) = produit de 5 termes = 105 = 102 + 3
10n × 10p = 10n + p
Ceci peut être fait pour toute autre valeur décimale notée a, et donc :
Remarquez que la formule transforme un produit de puissances en une puissance de la somme des exposants.
On peut envisager de calculer une puissance d’une puissance : (10n)p.
Par définition, 10n = 10 × 10 × … 10 produit de n termes
Donc la puissance p de cette valeur est : (10 × 10 × … 10)p = (10 × 10 × … 10) × (10 × 10 × … 10) × … (10 × 10 × … 10) dans lequel il y p couples de parenthèses.
Dans chaque paire de parenthèses, il y a n termes, et il y a p paires de parenthèses. Donc, il y a en tout n × p fois la valeur 10.
Pour fixer les idées, nous avons en particulier : (102)3 = (10 × 10) × (10 × 10) × (10 × 10) = 10 × 10 × 10 × 10 × 10 × 10 = 106. Pour être correct, il faut dire que l’on utlise là l’associativité du produit.En revenant à la définition, ceci représente 10n × p
On ne note pas le symbole du produit (×) : 10np
On vient donc de montrer (même si c’est de manière un peu informelle) que (10n)p = 10np
Ce que nous nous empressons de réécrire de manière générale :
Remarquez cette fois que la formule transforme une puissance de puissance en une puissance de produit des exposants.
Pour qu’une puissance existe, naturellement, il faut qu’il y ait au moins deux termes ! Donc, a1 n’est pas défini. Ceci est bien gênant, car une telle écriture peut très bien apparaître comme résultat d’un calcul. Que faire ?
Bien évidemment, si nous définissons a1 par une expression quelconque, il y a peu de chances pourqu’elle satisfasse la formule 1. Aussi, si nous voulons que les calculs soient les plus simples possibles, c’est bien de la première formule qu’il faut partir pour tenter une définition. On impose que cette formule soit aussi valable pour la puissance 1.
Dans cette formule, prenons p = 1 : an × a1 = an + 1. A gauche, an contient n termes, et à droite an + 1 contient (n + 1) termes. Pour que l’égalité soit conservée, il faut donc que a1 contienne exactement 1 terme, donc que :
Sur cette lancée, qu’en serait-il de 0 ? Autrement dit, pourrait-on définir, donner un sens à, a0 ?
Le même raisonnement que ci-dessus nous amène à partir de la formule 1, et à l’appliquer (l’imposer) avec p = 0 :
an × a0 = an + 0 = an.
A gauche, an contient n termes ; à droite, on retrouve les mêmes n termes. Donc, à gauche, la multiplication par a0 ne change pas la valeur. La seule possibilité est que :
Remarquez que la valeur 1 est la même, quelle que soit la valeur de a ! 1 = 20 = 30 = 40…
Pour les deux définitions que nous venons de proposer, remarquez que 0 est l’élément neutre de l’addition, et 1 celui de la multiplication.
L’opération puissance transforme l’élément neutre de l’addition en l’élément neutre de la multiplication. Les mathématiques montrent une magnifique cohérence !
Vous pourrez vérifier que la définition récursive donnée plus haut est valable en prenant maintenant pour base a0 = 1. On réservera cette formule pour des puissances entières, positives.
Ayant défini initialement les puissances pour p ≥ 2, nous venons de prolonger cette définition pour p = 1 puis p = 0. Maintenant, tout entier positif ou nul peut être un exposant. Que dire des entiers négatifs ?
Pour l’instant, on ne peut pas les considérer. Mais là encore, on peut envisager de les voir apparaître dans un calcul. En effet, si n est le résultat d’un calcul, rien n’empêche d’obtenir une valeur négative pour n, et de trouver a-3 par exemple. Une telle situation s’est produite dans le passé (lointain), et les mathématiciens en restaient là, sur une impossibilité de résoudre le problème. Mais là encore, nous allons trouver une méthode. Comme précédemment, pour que les calculs soient réguliers, il faut que la formule 1 soit valide avec la définition de la puissance négative. Donc :
an × a-p = an - p.
A gauche, nous avons un produit de n termes, multiplié par la valeur à déterminer de a-p. A doite, dans an - p, nous avons n - p termes, c’est-à-dire n termes, auquels on en a retranché p. Pour que ce soit égal à l’expression de gauche, il faut qu’il y ait le même nombre de termes, donc il faut que a-p retranche p termes aux n de an…
Pour retrancher ces p termes, il suffit de diviser p fois par a, c’est-à-dire diviser par ap. Et donc :
Exemple : on doit avoir a3 × a-2 = a3 - 2
(a × a × a) × (a-2) = a3 - 2 = a1 = a
Donc, a-2 retranche 2 termes a à gauche. Pour cela, a-2 divise deux fois par a, ce qu’on peut encore traduire par divise par a+2.
a-p divise par ap, ou encore multiplie par 1 / a-p
Maintenant, nous avons défini an pour toute valeur entière de n, positive, négative ou nulle, de telle manière que la formule 1 soit vérifiée :
On n’a pas noté l’opérateur de multiplication à gauche. Les symboles à droite signifient que la formule est valable pour tous les n, et pour tous les p, pris dans l’ensemble ℤ des entiers relatifs (c’est-à-dire positifs, négatifs, ou 0).
ℤ = {… -3, -2, -1, 0, 1, 2, 3, …}
Maintenant que nous avons défini les puissances en-dessous de 2, il faut vérifier que la formule 2 : (an)p = anp est toujours valide. Il faut passer en revue les valeurs de n et de p non considérées avant, donc 1, 0 et les valeurs négatives.
• Prenons d’abord n = 1. La formule devient (a1)p = a1 p. D’après la définition, a1 = a, et 1 p = p. Donc ap = ap est évidemment vérifié. Les mathématiciens disent trivialement, terme qui signifie tellement évident qu’aucune démonstration n’est nécessaire.
• Prenons maintenant n = 0. Il faut que (a0)p = a0 p. Le produit de p par 0 donne évidemment 0. Donc on a à droite a0 = 1. Mais à gauche, on a (a0)p = 1p = 1. Donc, l’égalité est réalisée.
• Considérons maintenant n négatif, avec p positif. La tâche n’est guère plus importante : (a-n)p = a-n p. Toujours en appliquant la définition, a-n = 1 / an. Donc il faut vérifier que (1 / an)p = a-n p.
Examinons d’abord le terme de gauche. (1 / an)p = (1 / a × a… × a)p = (1 / a × a… × a) × (1 / a × a… × a)… × (1 / a × a… × a).
Dans chaque parenthèse, il y a n termes, et il y a p parenthèses. Donc ceci est égal à 1 / (a × a… × a) où la parenthèse contient n p termes. C’est donc par définition 1 / an p. Et enfin, par définition de la puissance négative, 1 / an p = a-n p. cqfd
Ceci achève la démonstration pour les valeurs de n 1, 0 et négatives. Il est facile de faire le même genre de travail pour les valeurs de p, ce qui achèverait la démonstration, et que nous laissons au lecteur. La méthode est toujours la même : il faut revenir aux définitions.
Nous venons donc de vérifier la formule 2 pour tous les entiers relatifs affectés à n. Il nous reste à faire la même chose pour p.
• Commençons par p = 1. Il faut (an)1 = an 1. A gauche, élever une valeur quelconque à la puissance 1 ne la change pas. Donc le terme de gauche vaut an. A droite, on an 1 = an, même valeur qu’à gauche. Donc la formule 2 est respectées pour p = 1.
• Pour p = 0 : (an)0 = an 0. On élève, à gauche et à droite, des valeurs à la puissance 0. Puisque tout valeur à la puissance 0 vaut 1, l’égalité est trivialement vérifiée.
• Enfin, pour les valeurs négatives de p : (an)-p = an (-p). On peut d’abord écrire : (an)-p = (1 / (an))p en utilisant la définition de la puissance négative. 1 / (an) s’écrit 1 / (a × a… ×a) avec n termes a. La puissance p de cette valeur s’écrit (1 / (a × a… ×a)) × (1 / (a × a… ×a))… × 1 / (a × a… ×a), avec p parenthèses. On a donc au dénominateur n × p fois a, donc anp. Puisque c’est au dénominateur, ça représente a-np. Pour le terme de droite, il suffit de faire le produit des exposants pour obtenir an (-p) = anp. Là encore, l’égalité est vérifiée.
Donc, les définitions que nous avons imposées sont telles que les formules sont maintenant valables pour toutes les valeurs entières, positives, nulles ou négatives.
| an = a × a × … × a produit de n termes |
| a1 = a |
| a0 = 1 |
| a-p = 1 / ap |
| an ap = an + p ∀ n, p ∈ ℤ |
| (an)p = anp ∀ n, p ∈ ℤ |
L’identité s’écrit (a + b)2 = a2 + 2 a b + b2
Il est très facile de la démontrer algébriquement : (a + b)2 = (a + b) (a + b)
Pour calculer le produit de ces deux facteurs, on additionne les produits de chaque couple de termes. Les couples de termes sont mis en lumière ci-dessous :
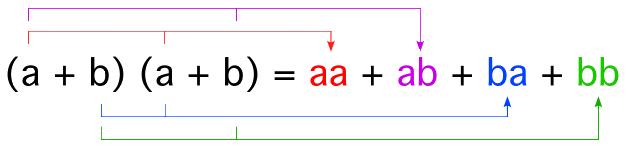
Le produit étant commutatif, ab = ba, et donc les deux termes se concentrent en 2 ab :
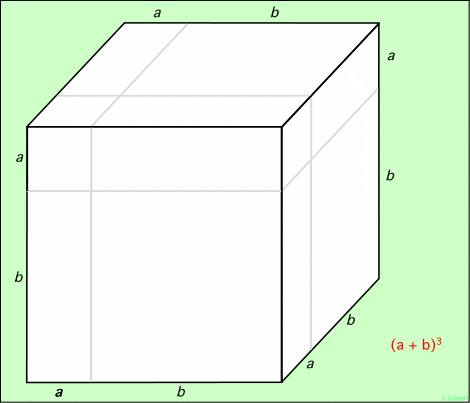
Mais on peut voir cette égalité sous une forme géométrique, peut-être plus parlante. Un carré (algébrique) est la mesure de la surface d’un carré (géométrique). Ainsi, a2 mesure la surface d’un carré de côté a. Plus généralement, la surface d’un rectangle de côtés a et b est le produit ab de ses côtés. Le carré ci-dessous se décompose en quatre parties :
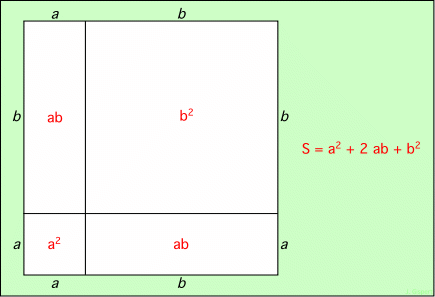
Tout d’abord, en bas à gauche, un petit carré de côté a. Sa surface, notée en rouge en son centre, vaut a2. Ensuite, on trouve un second carré, plus grand, de côté b, en haut et à droite. Sa surface est donc b2. La figure se complète par un rectangle en haut à gauche, qui s’appuie sur les deux carrés, et dont les côtés sont par conséquent a et b. Ce rectangle a une surface valant ab. Enfin, en bas et à droite, un autre rectangle qui s’appuie sur d’autres côtés des carrés, et dont les côtés sont également a et b. Sa surface vaut par conséquent aussi ab.
La figure complète est un carré, puisque chaque côté comporte deux longueurs, a et b dont la somme est a + b. Et sa surface est la somme des surfaces de chaque composante, donc a2 + b2 + ab + ab. On ajoute les deux quantités égales, et on réarrange en : S = a2 + 2 ab + b2. Cette formule est donc une représentation de la surface totale du grand carré.
Alternativement, on peut calculer directement sa surface. Puisque son côté vaut a + b, sa surface s’obtient en multipliant a + b par a + b, c’est-à-dire en prenant le carré de a + b, soit (a + b)2. On le voit sur la figure ci-dessous :
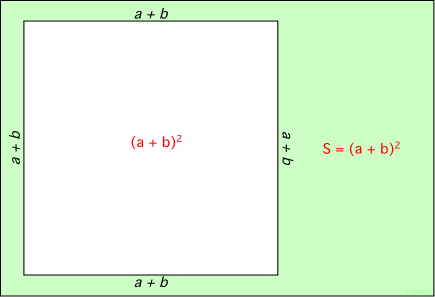
Nous venons de trouver deux formules différentes, qui représentent toutes deux la même quantité : la surface du grand carré. Par conséquent, ces deux quantités sont égales, et l’on peut écrire : (a + b)2 = a2 + 2 ab + b2. Ceci est donc une interprétation géométrique de la formule trouvée algébriquement plus haut.
Pourrait-on avoir une formule semblable avec des cubes ? Bien sûr ! Algébriquement, il suffit de reprendre la définition du cube, et d’effectuer :
(a + b)3 = (a + b) (a + b) (a + b) = (a + b) (a + b)2 = (a + b) (a2 + 2 ab + b2)
où l’on a remplacé le produit des deux derniers termes par la formule équivalente qu’on vient de déterminer. Il nous reste seulement à effectuer ce produit. Comme plus haut, c’est la somme des produits de chaque couple de termes :
(a + b) (a2 + 2 ab + b2) = a3 + 2 a2b + ab2 + a2b + 2 ab2 + b3
et en regroupant les termes égaux :
Y aurait-il aussi une interprétation géométrique ? Oui, là encore… Evidemment, à la place de surfaces, on aura des volumes. Repartons de la figure en surface précédente, et donnons-lui une épaisseur.
On construit ainsi une plaque d’épaisseur a, représentée ci-dessous :
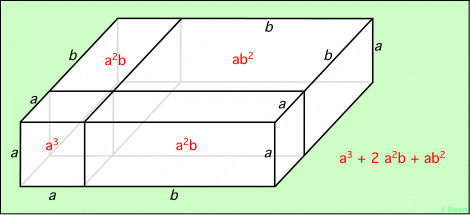
Il est facile d’en évaluer les différents volumes : on note la longueur de chaque côté, et on multiplie. Le résultat est noté en bas à droite de la figure.
Construisons maintenant un autre volume, en donnant à la surface précédente une épaisseur b :
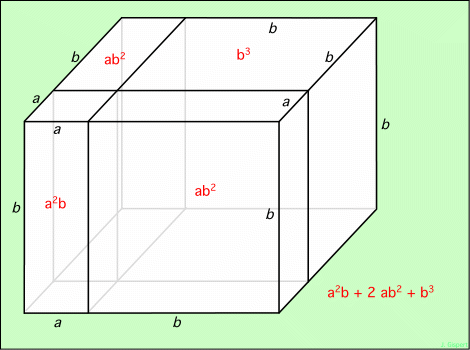
L’évaluation des volumes est tout aussi simple. La somme est notée en bas à droite.
Il ne reste qu’à empiler les deux volumes à peine construits :
Le volume total des deux parties est donc :
a3 + 2 a2b + ab2 + a2b + 2 ab2 + b3
Le plus en rouge sépare les deux expressions provenant des deux parties de la figure. Le résultat est :
a3 + 3 a2b + 3 ab2 + b3
Par construction, on a bien un cube de côté a + b. Par conséquent son volume est (a + b)3. L’égalité de ces deux expressions du volume donne la formule annoncée.
Pourrait-on aller encore plus loin, et envisager une puissance 4 ? Bien sûr, il suffit, algébriquement, de multiplier le dernier résultat par a + b, pour passer de la puissance 3 à la puissance 4. Le calcul donne :
(a + b)4 = a4 + 4 a3b + 6 a2b2 + 4 ab3 + b4
On voit apparaître une forme facile à prévoir. Tous les termes de la somme totalisent les mêmes exposants : le premier a l’exposant 4 pour a, et 0 pour b (puisque a4 = a4 × 1 = a4 × b0 = a4 b0) ; le second a 3 pour a, 1 pour b ; le troisième 2 pour chacun ; le quatrième 1 pour a et 3 pour b ; et enfin le dernier 4 pour b et 0 pour a. On peut prévoir que les puissances supérieures seront construites de la même manière. D’ailleurs, les constructions géométriques ci-dessus nous ont montré que pour la puissance 2, c’est une somme de surfaces. Toute surface est le produit de deux longueurs, donc il doit y avoir exactement deux termes, égaux (comme dans a2, un carré), ou différents (comme dans ab, un rectangle). Pour le cube, c’est une somme de volumes, donc trois termes…
Mais au-delà de 3, l’intuition géométrique ne peut pas être poursuivie… tout au moins avec des mathématiques élémentaires. Il existe des géométries dans des espaces ayant plus de trois dimensions, mais nous ne sommes pas capables de les visualiser dans notre espace à trois dimensions.
Ceci est une belle illustration de l’unité entre l’algèbre et la géométrie. C’est une marque de la construction logique des mathématiques. La notion de puissance commence par le carré, qui est la mesure de la surface d’un carré ! Ensuite, on a défini le cube, qui mesure le volume d’un cube. Après, la notation algébrique permet facilement de construire des puissances supérieures, aqlors que la géomtérie s’est trouvée limitée. Jusqu’à ce qu’on construise des géométrie sur des espaces à plus de trois dimensions…
Un raisonnement sur la forme des expressions permet de calculer une puissance quelconque. Le problème est de déterminer les coefficients, et le triangle de Pascal permet de le faire. On écrit tout d’abord 1 sur la première ligne, puis 1, et 1 sur la seconde. La première ligne correspond à (a + b)0 qui vaut 1, la seconde à la puissance 1, qui s’écrit 1 a + 1 b. Ensuite, pour chaque ligne successive, on additionne les deux termes qui sont dans la ligne immédiatement au-dessus, dans la case au-dessus et celle qui est à sa gauche. Voici quelques lignes du triangle :
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
| 1 | 3 | 3 | 1 | ||
| 1 | 4 | 6 | 4 | 1 | |
| 1 | 5 | 10 | 10 | 5 | 1 |
On peut continuer ainsi, après avoir vérifié que les expressions que nous avons obtenues plus haut sont bien en accord avec les coefficients obtenus ici.
Dans le volume que nous avons dessiné, la face supérieure représente le dessin des surfaces, et montre que (a + b)2 = a2 + 2 ab + b2. Les volumes montrent de leur côté que (a + b)3 = a3 + 3 a2b + 3 ab2 + b3. Une figure à 4 dimensions (que l’on ne peut pas dessiner, mais qui est imaginable, et mathématiquement constructible) exhiberait ces deux identités sur des 'faces', et en plus l’identité (a + b)4 = a4 + 4 a3b + 6 a2b2 + 4 ab3 + b4. On peut imaginer aussi la dimension 5, et ainsi de suite. Un hypervolume de dimension n (volume d’un hypercube de dimension n), exhiberait ainsi toutes les identités remarquables jusqu’à la puissance n, comme décomposition de certaines faces, de dimension 2 pour la puissance 2, de dimension 3 pour la puissance 3…
Si on part de 104, on obtient 103 en divisant par 10 : 103 = 104 / 10 ;
de même, partant de 103, on obtient 102 en divisant par 10 : 102 = 103 / 10 ;
puis 102 donne 101 = 10 en divisant par 10 une nouvelle fois : 101 = 102 / 10 ; 101 = 100 / 10 = 10.
On voit donc tout d’abord que 101 = 10.
Que se passe-t-il si nous divisons cette dernière valeur par 10 ? 101 / 10 = 10 / 10 = 1. Or dans notre procédé nous avons à chaque opération retranché 1 à la puissance : on est passé de la puissance 4 à la puissance 3, puis de 3 à 2 … Maintenant, partant de 1, nous obtenons 0 !
On définit donc une nouvelle puissance ainsi :
100 = 1
On peut représenter tout ce qui vient d’être défini sous forme de tableau, le nombre du haut étant la puissance, et celui du bas la valeur de 10 élevé à cette puissance :
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 10n | 1 | 10 | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 |
Bien sûr, tout ce que nous venons de dire peut se répéter pour d’autres nombres : on définit les puissances d’un nombre quelconque x de la manière suivante :
xn = produit de n termes égaux à x
La dernière étape de notre raisonnement ci-dessus nous a montré qu’on passait de 101 = 10 à 100 = 10 / 10 = 1. De même, x1 = x et donc x0 = x / x = 1.
Donc tout nombre à la puissance 0 donne 1.
Les puissances négatives
Et si nous continuions notre procédé ?
Nous nous sommes arrêtés à 100 = 1 ; si nous divisons encore par 10, nous obtenons 1/10 et nous retranchons 1 à la puissance. D’où, naturellement :
10-1 = 1/10
On continue ?
10-2 = 1/100
10-3 = 1/1000
etc.
Maintenant, nous avons défini toutes les puissances entières de 10. Ce que nous avons fait sur cette valeur particulière peut se faire sur tout nombre.
La puissance 2 porte un nom particulier : on l’appelle carré, car c’est elle qui donne la surface d’un carré.
La puissance 3 de même se nomme cube, car elle donne le volume d’un cube.
On s’arrête là, car notre univers ne présente que 3 dimensions (d’espace)… à moins que la théorie des supercordes ne nous en révèle d’autres, mais celles-ci, si elles existent, échappent à nos sens.
| 10-6 | 10-5 | 10-4 | 10-3 | 10-2 | 10-1 | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| 0,000001 | 0,00001 | 0,0001 | 0,001 | 0,01 | 0,1 | 1 | 10 | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 |
| micro | milli | hecto | kilo | méga |
On remarque dans ce tableau que pour écrire sous forme de nombre la puissance 10n, il faut écrire "1" suivi de n zéros. Ainsi 103 s’écrit "1" suivi de trois "0".
De même, pour écrire 10-n, il faut écrire "0", suivi de n-1 zéros, suivi de 1. Ainsi 10-3 s’écrit "0", suivi de deux 0, suivi de 1 (dans les deux cas, il y a n chiffres, soit avant, soit après la virgule).
Calcul des puissances
Le produit de deux puissances peut s’écrire sous une forme simple. Voyons d’abord un exemple :
105 × 103 = 100.000 × 1.000 = 100.000.000 = 108
Ceci peut se faire plus généralement :
10n × 10p = ("1" suivi de n zéro) × ("1" suivi de p zéro) = ("1" suivi de n+p zéro) = 10n+p
Par conséquent : 10n × 10p = 10n+p
Si l’une des deux puissances est négative, le résultat est le même :
105 × 10-3 = 100.000 × 0,001 = 1.000 = 103
d’où 10n × 10-p = 10n-p
On pourrait vérifier aussi que le résultat se conserve si les deux puissances sont négatives. Au bout du compte, la formule est vraie pour tout n et p entiers négatifs, positifs ou nuls.
Exemple
Une année-lumière est la distance parcourue par la lumière en une année. La lumière se propage à la vitesse de 300.000 kilomètres par seconde. 300.000 = 3 × 100.000 = 3 105. On peut déjà écrire que la vitesse de la lumière vaut 3 105 kilomètres par seconde.
Transformons maintenant cette valeur dans les unités internationales, c’est-à-dire en mètres par seconde. Un kilomètre vaut 1.000 mètres, c’est-à-dire 103 mètres. Donc la vitesse de la lumière est de 3 105 fois 103 mètres par seconde = 3 105x 103 mètres par seconde = 3 105+3 mètres par seconde = 3 108 mètres par seconde.
Pour connaître l’année-lumière en mètres, il faut multiplier la vitesse par le temps ; calculons ce temps. L’année contient 365 jours de 24 heures, chaque heure est composée de 60 minutes de 60 secondes.
1 heure = 60 × 60 secondes = 3.600 secondes
1 année = 365 × 24 heures = 8.760 heures
d’où : 1 année = 8.760 × 3.600 secondes = 31.536.000 secondes
Une année-lumière vaut 3 108 mètres par seconde × 31.536.000 secondes = 3 108 × 31.536.000 = 3 × 31.536.000 108 = 94.608.000 108 mètres.
Cette valeur est trop précise pour qu’on puisse la retenir. Changeons-la un peu pour la simplifier. 94.608.000 est très proche de 94.000.000, qui est proche de 100.000.000. Maintenant, nous n’avons plus qu’un 1 suivi de 8 zéros. Ce nombre peut donc s’écrire sous forme d’une puissance de 10 :
100.000.000 = 108
L’année-lumière est donc très proche de : 108 × 108 mètres = 108+8 mètres = 1016 mètres
Si on l’écrit sous forme de nombre : 1016 mètres = 10.000.000.000.000.000 mètres, nombre absolument illisible !
Si on veut exprimer l’année-lumière en kilomètres, il suffit d’enlever 3 zéros à ce nombre, donc de retrancher 3 à la puissance de 10 :
1 AL = 1013 kilomètres
Préfixes
Pour parler simplement, on définit des préfixes correspondant à des coefficients standards :
hecto = 102 = 100
kilo = 103 = 1.000
| femto | pico | nano | micro | milli | kilo | méga | giga | téra | péta |
| 10-15 | 10-12 | 10-9 | 10-6 | 10-3 | 103 | 106 | 109 | 1012 | 1015 |
Le pulsar milliseconde tourne sur lui-même en une milliseconde !
Le laser femtoseconde est un laser dont l’impulsion lumineuse dure une femtoseconde, soit un millionième de milliardième de seconde !
Les constantes physiques
Nombre d’Avogadro N = 6,022 1023 mol-1
Constante de Boltzmann kB = 8,617 10-5 eV K-1
Constante de Plank h = 4,136 10-15 eV s
Vitesse de la lumière dans le vide c = 299.792.458 m s-1 proche de 300.000 km s-1
Charge élémentaire de l’électron e = 1,602 10-19 C
Masse de l’électron mB = 9,109 10-31 kg
Masse du proton mp = 1,673 10-27 kg
Masse du neutron mn = 1,675 10-27 kg
Trigonométrie
La trigonométrie a été inventée il y a très longtemps, pour résoudre les problèmes qui se posent dans un triangle (d’où le nom, du grec tri trois, gonos angle).
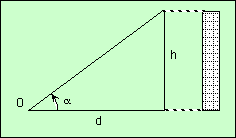
Comment mesurer la hauteur d’un immeuble, sans dérouler une corde depuis le toit ? On peut faire un dessin et remarquer que plusieurs immeubles de tailles différentes, mais situés à des distances différentes, sont vus sous la même hauteur apparente. Cette hauteur se matérialise par l’angle α sous lequel on voit l’immeuble.
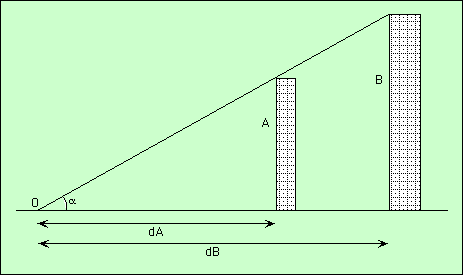
L’idée de base consiste donc à trouver un immeuble assez bas pour pouvoir le mesurer, et à déterminer la hauteur du grand en faisant une proportion :
hauteurB / hauteurA = distanceB / distanceA
On connait hauteurA, distanceA et distanceB, on en déduit hauteurB = (distanceB / distanceA) × hauteurA.
Pour faire cette mesure, on a utilisé une propriété des triangles semblables : leurs côtés sont dans le même rapport. Deux triangles sont semblables s’ils ont la même forme, mais sont de dimensions différentes. C’est exactement ce qui se passe si vous faites des photos d’un triangle, avec des réglages de zoom différents. Sur les photos, vous verrez toujours le même triangle, mais avec des tailles différentes.
Etude des rapports
Les rapports de longueurs que l’on peut définir dans les triangles sont donc très importants, et l’idée est vite venue de les étudier et de formaliser les calculs associés. C’est ce que fait la trigonométrie.
Reprenons le rapport précédent, en simplifiant un peu l’écriture :
hauteurB / hauteurA = distanceB / distanceA
réécrit
hB / hA = dB / dA
De chaque côté de l’égalité on voit des grandeurs dépendant des deux immeubles. On peut réécrire le rapport en mettant du même côté le grandeurs qui caractérisent chacun :
hB / dB = hA / dA
Ceci exprime que le rapport hauteur / distance est le même pour tous les triangles semblables. C’est-à-dire pour tous les triangles qui ont les mêmes angles. On va donc caractériser les angles (cette famille de triangles), par le rapport hauteurA / distanceA en particulier.
Triangles particuliers
Les triangles les plus divers sont trop complexes pour être apréhendés facilement. En effet, avec un angle α donné, on peut avoir n’importe quelle valeur pour les deux autres angles :
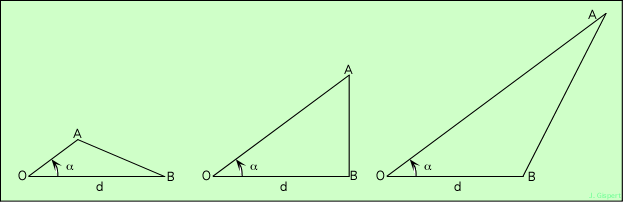
Ces trois triangles partagent le même angle α (celui auquel on va s’intéresser), et aussi la même base OB = d. Mais les autres côtés sont différents. Celui du milieu est particulier : il est rectangle en B (l’angle B vaut 90°). Pour représenter l’angle α, on peut choisir ce triangle particulier. C’est ce choix qui est la base de la trigonométrie.
En résumé : la trigonométrie est l’étude des rapports dans les triangles, et pour pouvoir les caractériser, on choisit les triangles rectangles comme représentants.
Fonctions trigonométriques
On définit trois fonction de base : le sinus, le cosinus et la tangente. Chacune correspond à un rapport dans un triangle rectangle. Considérez donc le triangle rectangle au centre de la figure.
| Le sinus (noté sin) est le rapport du côté opposé sur l’hypothénuse : | sin α = AB / OA |
| Le cosinus (noté cos) est le rapport du côté adjacent sur l’hypothénuse : | cos α = OB / OA |
| La tangente (notée tg) est le rapport du côté opposé sur le côté adjacent : | tg α = AB / OB |
Nous pouvons déjà trouver une propriété, en divisant le sinus par le cosinus :
sin α / cos α = (AB / OA) / (OB / OA) = (AB / OA) x (OA / OB) = AB / OB
On constate que c’est le rapport qui définit la tangente. Donc :
sin α / cos α = tg α
On voit tout de suite que si l’angle est nul, la hauteur de l’immeuble est nulle aussi. Si l’angle vaut 90°, la tangente (la hauteur) est infinie.
Pour quelle valeur de l’angle la hauteur vaut-elle 1 ? Si on refait un dessin montrant cette situation, on s’aperçoit qu’on a construit un carré, et que le triangle CPS est la moitié du carré. Donc l’angle recherché vaut la moitié d’un angle droit, 45°.
Supposons qu’on ait réussi à calculer les valeurs de cette fonction pour un grand nombre de valeurs de l’angle. Ces valeurs seront notées dans une table sous la forme :
| angle | tangente | angle | tangente |
|---|---|---|---|
| 0° | 0 | 50° | 1,19 |
| 5° | 0,0875 | 55° | 1,43 |
| 10° | 0,176 | 60° | 1,73 |
| 15° | 0,268 | 65° | 2,14 |
| 20° | 0,364 | 70° | 2,75 |
| 25° | 0,466 | 75° | 3,73 |
| 30° | 0,577 | 80° | 5,67 |
| 35° | 0,700 | 85° | 11,4 |
| 40° | 0,839 | 90° | infinie |
| 45° | 1,000 |
Alors, on peut calculer la hauteur d’un immeuble simplement en mesurant l’angle sous lequel on le voit et sa distance :
hauteur = distance × tg α
Cercle trigonométrique
Pour tenir compte de tous les angles possibles, on définit le cercle trigonométrique dans lequel ils vont s’inscrire/ Par définition, le cercle trigonométrique est un cercle de rayon 1 (ce qui se justifie puisqu’on ne calcule que des rapports), avec deux axes orientés perpendiculaires :
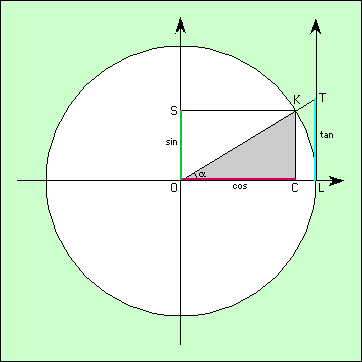
Donc sur le schéma, OL = OK = 1.
La tangente de l’angle α est notée tan, et sa mesure est la longueur du segment LT.
Sur le cercle trigonométrique, on définit encore deux fonctions, nommées sinus et cosinus. Comme la tangente, ce sont des rapports :
sin α = côté opposé / hypothénuse = CK / OK
cos α = côté adjacent / hypothénuse = OC / OK
Les triangles OCK et OLT étant semblables, LT / CK = OL / OC
LT = tg α ; CK = sin α ; OL = 1 ; OC = cos α
Par substitution il vient immédiatement :
tg α / sin α = 1 / cos α
ce qui s’écrit plus simplement :
tg α = sin α/ cos α
Relation fondamentale
Dans le triangle rectangle OCK, on peut écrire le théorème de Pytagore :
OC2 + CK2 = OK2
par substitution encore il vient :
cos α2 + sin α2 = 12
que l’on écrit :
sin α2 + cos α2 = 1
Etant donné que le cercle trigonométrique a un rayon unité, on voit que le cosinus ne peut pas dépasser 1. Si l’angle croît jusqu’à 90°, le cosinus décroît jusqu’à 0. L’angle dépassant 90°, le cosinus passe de l’autre côté, il est orienté dans l’autre sens, et devient donc négatif. Sa valeur va décroître jusqu’à l’angle de 180°, et atteindra -1. Ensuite, si l’angle augmente toujours, le cosinus remonte de -1 jusqu’à 0 pour α = 270°, et ensuite jusqu’à 1 pour 360°
Rien ne nous empêche d’entamer un deuxième tour, avec un angle croissant toujours au-dessus de 360°. Les valeurs du cosinus seront les mêmes que précédemant. Donc, on a la relation fondamentale :
cos (360° + α) = cos α
On peut d’ailleurs faire autant de tours qu’on veut, et donc pour toute valeur de n :
cos (n 360° + α) = cos α
Une telle fonction est dite périodique, puisque pour des valeurs croissantes de la variable, elle reprend les mêmes valeurs dans le même ordre. La période est de 360°.
Le sinus est symétrique du cosinus.
Tout ce que nous avons vu pour le cosinus peut s’adapter au sinus :
pour α = 0, il vaut 0 ;
pour a = 90°, il vaut +1 ;
pour a = 180°, il vaut 0,
et pour a = 270°, il vaut -1.
Le sinus lui aussi est périodique, de période 360°.
sin (n 360° + α) = sin α
Radians
La plupart du temps, les mathématiciens n’utilisent pas les degrés, mais les radians pour la mesure des angles.
La définition est simple : un tour complet, qui vaut 360°, vaut par définition 2 π radians. D’où la correspondance :
| degrés | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| radians | 0 | π / 6 | π / 4 | π / 3 | π / 2 | π | 3 π / 2 | 2 π |
La conversion est facile. Soit à trouver la valeur en radians d’un angle de 23°. On écrit la correspondance :
180° → π
23° → x
Donc : 180° / 23° = π / x
x = π × 23° / 180° = 0,4014 radians
Dans l’autre sens, la conversion est tout aussi aisée :
180° → π
y° → 0,4014
Donc : 180° / y° = π / 0,4014
y = 180 × 0,4014 / π = 22,998°
On peut voir une petite difficulté si l’angle n’est pas un nombre entier de degrés. Prenons un exemple encore. Trouver la valeur en radians de l’angle 23° 42′ 12"
Nous allons d’abord convertir cette valeur sexagésimale en valeur décimale :
1′ → 60″
x′ → 12″
d’où : 1′ / x′ = 60″ / 12″
et x′ = (12″ / 60″) × 1′ = 0,2′
Par conséquent, 12″ font 0,2′. Et 42′ 12″ font 42,2′.
L’angle à déterminer est maintenant écrit : 23° 42,2′. Il ne contient plus de secondes. On le traduit en degrés décimaux pareillement :
1° → → 60′
x° → 42,2′
d’où : 1° / x° = 60′ / 42,2′
et x° = 42,2′ / 60′ = 0,7033°
Donc l’angle vaut 23,7033° décimaux.
Maintenant, on peut le convertir en radians comme précédement :
180° → π
23,7033° → x
Donc : 180° / 23,7033° = π / x
x = π × 23,7033° / 180° = 0,4137 radians
Relations
Il existe de très nombreuses relations entre les trois fonctions trigonométriques que nous avons définies. Ces relations permettent de faire des calculs, en remplaçant par exemple une somme de terme par un produit. Elles sont très utiles.
Voici un tableau qui les réunit :
| sin2 a + cos2 a = 1 | tg a = sin a / cos a | cos2 a = 1 / (1 + tg2 a) | sin2 a = tg2 a / (1 + tg2 a) | |
| cos (- a) = cos a | cos (π - a) = - cos a | cos (π + a) = - cos a | cos (π / 2 - a ) = sin a | cos (π / 2 + a ) = - sin a |
| sin (- a) = - sin a | sin (π - a) = sin a | sin (π + a) = - sin a | sin (π / 2 - a) = cos a | sin (π / 2 + a) = cos a |
| tg (- a) = - tg a | tg (π - a) = - tg a | tg (π + a) = tg a |
Ci-dessous, le tableau donne les fonction trigonométriques de sommes d’arc (colonne de gauche). On en déduit immédiatement (colonne centrale) des formules concernant les arcs doubles. Et la troisième colonne donne des formules reliant les arcs aux arcs moitié.
Les produits étant parfois plus faciles à traiter que les sommes, on a intérêt à transformer des sommes en produits. C’est ce que permettent ces formules. Par exemple, cos a cos b - sin a sin b peut être remplacé par cos (a + b), qui ne contient qu’un seul terme. Ces formules montrent des changements de forme des expressions. On utilise souvent ce changement de forme pour faciliter les calculs.
| cos (a + b) = cos a cos b - sin a sin b | cos 2 a = cos2 a - sin2 a cos 2 a = 2 cos2 a - 1 | 1 + cos a = 2 cos2 a/2 |
| cos (a - b) = cos a cos b + sin a sin b | cos 2 a = 1 - 2 sin2 a sin 2 a = 2 sin a cos a | 1 - cos a = 2 sin2 a/2 |
| sin (a + b) = sin a cos b + sin b cos a | tg 2 a = 2 tg a /(1 - tg2 a) | sin a = 2 sin a/2 cos a/2 |
| sin (a - b) = sin a cos b - sin b cos a | cos2 a = (1 + cos 2a) / 2 | cos a = (1 - t2)/ (1 + t2) (t = tg a/2) |
| tg (a + b) = (tg a + tg b) / (1 - tg a tg) b | sin2 a = (1 - cos 2a) / 2 | sin a = 2 t / (1 + t2) |
| tg (a - b) = (tg a - tg b) / (1 + tg a tg b) | tg2 a = (1 - cos 2a) / (1 + cos 2a) | tg a = 2 t / (1 - t2) |
Dans ce tableau, vous voyez la variable t = tg (a / 2) introduite. Cette variable est très importante, car les expressions correspondantes des fonctions sin, cos et tg sont des expressions rationnelles (des quotients). On peut alors transformer des expressions trigonométriques en expressions rationnelles. Ceci est très utile en intégration par exemple.
Enfin, voici les formules d’addition des arcs
| cos a cos b = [cos (a + b) + cos (a - b)] / 2 | cos p + cos q = 2 cos (p + q)/2 cos (p - q)/2 | tg p + tg q = sin (p + q) / cos p cos q |
| sin a sin b = [cos (a - b) - cos (a + b)] / 2 | cos p - cos q = - 2 sin (p + q)/2 sin (p - q)/2 | tg p - tg q = sin (p - q) / cos p cos q |
| sin a cos b = [sin (a + b) + sin (a - b)] / 2 | sin p + sin q = 2 sin (p + q)/2 cos (p - q)/2 | sin p - sin q = 2 sin (p - q)/2 cos (p + q)/2 |
Les mathématiques sont un jeu. Dommage que ce ne soit pas toujours évident… Les mathématiciens sont ceux qui l’ont compris !
Nous allons jouer avec des 1 et des 0. Pour jouer, il faut des règles. La première que nous utiliserons est le carré : x2 = x multiplié par x, soit x × x.
Le cube est x3 = x multiplié par x multiplié par x, soit x × x × x.
On peut continuer, et la puissance n de x est le produit de n termes égaux à x.
On peut étendre un peu cela en admettant le produit de 1 terme égal à x, ce qui donne x = x1.
Avec les 0 et les 1, on peut noter la dizaine, la centaine, le millier… qui sont des puissances de 10. Plaçons-les dans un tableau, en notant la puissance de 10 et sa valeur (10, 100, 1.000…), ainsi que le nombre de zéros :
| puissance | nombre | nb. de zéros |
| 104 | 10.000 | 4 |
| 103 | 1.000 | 3 |
| 102 | 100 | 2 |
| 101 | 10 | 1 |
Le nombre de zéros est égal à l’exposant de 10 : 10n s’écrit 1 suivi de n zéros (par exemple, 103 s’écrit bien 1 suivi de 3 zéros). Il est évident que l’on peut prolonger ce tableau vers le haut tant qu’on veut (105 = 100.000 avec 5 zéros, 106 = 1.000.000 avec 6 zéros…). Mais vers le bas ?
Poursuivons notre jeu de réflexion, pour trouver la suite logique de la série. Il faut ajouter une ligne en bas du tableau, qui soit structurée comme les autres :
| puissance | nombre | nb. de zéros |
| 104 | 10.000 | 4 |
| 103 | 1.000 | 3 |
| 102 | 100 | 2 |
| 101 | 10 | 1 |
| ? | ? | ? |
Partant de la première ligne (104, 10.000), il faut diviser le nombre par 10 pour atteindre la suivante (103, 1.000). Et le nombre de zéros (4) diminue d’une unité (3). Idem pour les lignes en-dessous. Alors, partant de la dernière ligne remplie (qui contient 10), il faut diviser 10 par 10, ce qui donne 1. Il faut aussi diminuer d’une unité l’exposant, ce qui donne 100. Enfin, le nombre de zéros est nul. Voici le résultat :
| puissance | nombre | nb. de zéros |
| 104 | 10.000 | 4 |
| 103 | 1.000 | 3 |
| 102 | 100 | 2 |
| 101 | 10 | 1 |
| 100 | 1 | 0 |
Pour que ceci soit cohérent, il faut définir 100 = 1. C’est bien une extension de la définition de puissance, car l’expression produit de zéro termes n’a pas de sens
Rien ne nous empêche de continuer à jouer, en prolongeant le tableau vers le bas (en divisant à chaque étape la ligne précédente par 10) :
| puissance | nombre | nb. de zéros |
| 104 | 10.000 | 4 |
| 103 | 1.000 | 3 |
| 102 | 100 | 2 |
| 101 | 10 | 1 |
| 100 | 1 | 0 |
| 10-1 | 0,1 | -1 |
| 10-2 | 0,01 | -2 |
Il y a un petit soucis. La méthode de construction utilisée, qui produit bien ce que l’on veut pour des valeurs plus grandes que 1, produit pour 0,1 et 0,01 un nombre de zéros négatif ! Doit-on rejeter la méthode, ou bien trouver une interprétation qui la sauve ? C’est la seconde possibilité qu’on choisit. Elle est simple : il suffit de considérer que, si le nombre de zéros est négatif, il y a un zéro avant la virgule, les autres après la virgule. Et le 1 est à droite au lieu d’être à gauche.
Comme nous l’avons fait plus haut pour 100, on voit qu’il faut définir 10-1 = 0,1 et 10-2 = 0,01. Remarquez que 0,1 = 1/10 et 0,01 = 1/100. On peut écrire donc :
10-1 = 1/10, 10-2 = 1/100.
Mais 10 = 101 et 100 = 102. On aboutit à :
10-1 = 1 / 101 et 10-2 = 1 / 102
On doit continuer, et définir pour un entier n ≥ 1 quelconque :
10-n = 1 / 10n
Maintenant, on est capable de donner une valeur pour toute puissance entière de 10. C’est une amélioration importante, mais on sent bien les limitations qu’il y a encore : pourquoi se limiter à des puissances de 10, et pourquoi des puissances entières ?
Nous avons utilisé les puissances de 10 parce que nous avons 10 doigts (c’est comme ça que les humains ont appris à compter, sur les doigts). Mais on peut procéder de la même façon avec 2 : le problème, c’est qu’on ne peut plus compter le nombre de zéros ! C’est normal, puisque notre numération a choisi 10 pour s’exprimer. On retrouve exactement le nombre de zéros si on écrit les nombres en binaire !
La numération choisie montre, ou cache, une propriété plus fondamentale et plus simple : le nombre de zéros dans notre numération habituelle correspond au nombre de facteurs 10 utilisés. C’est une façon équivalente de définir la puissance.
104 = 10 × 10 × 10 × 10 × = 10.000 puissance 4, 4 facteurs, 4 zéros
Dans le tableau, lorsqu’on passe d’une ligne à celle de dessous en divisant par 10 et en retranchant 1 zéro, on enlève un facteur 10. On peut faire exactement la même chose avec les puissances de 2, sauf compter les zéros si on représente les nombres en décimal (mais ce serait possible en représentation binaire) :
| puissance | nombre | nb. de facteurs |
| 24 | 16 | 4 |
| 23 | 8 | 3 |
| 22 | 4 | 2 |
| 21 | 2 | 1 |
| 20 | 1 | 0 |
| 2-1 | 1/2 = 0,5 | -1 |
| 2-2 | 1/4 = 0,25 | -2 |
Les formules de calcul que nous avons trouvées subsistent. Par exemple, 2-n = 1 / 2n, on le voit dans le tableau
Choisissant 10, ou bien 2, on obtient ces relations. Quel que soit le nombre choisi (appelons-le x), sa puissance 4 par exemple sera le produit de 4 facteurs x. Et pour passer à la puissance 3 il faudra diviser par x, donc enlever un facteur. On obtiendra donc comme ci-dessus qu’en passant de la puissance 2 (x2 = x × x) à la puissance 1, on divise par x, ce qui revient à supprimer 1 facteur (donc retrancher 1 à la puissance).
Et en continuant, on définit la puissance 0 : x0 = (1 facteur de moins, donc zéro facteurs) on divise donc par x (x / x = 1)
On définit de la même manière les puissances négatives.
Donc, nous pouvons définir pour tout nombre x, ses puissances entières, positives, nulle ou négative.
La racine carrée d’un nombre, par exemple 4, est le nombre qui, élevé au carré, donne 4. Il est évident que c’est 2 (2 × 2 = 4). Généralement, la racine carrée de x2 est x.
Ce qu’on écrit : √(x2) = x.
Si on prend la racine carrée du carré de x, on retrouve x, comme si on n’avait rien changé ! Pareillement, multiplier un nombre par 2 et diviser le résultat par 2 ne change rien. On dit que deux opérations qui, enchaînées, ne changent rien, sont inverse l’une de l’autre. La division par 2 est l’inverse de la multiplication par 2.
Et pareillement, la racine carrée est l’inverse de l’élévation au carré. On tire partie de cette remarque. Puisque la racine carrée est l’opération inverse de l’élévation au carré (qui est une puissance), elle est de même nature, c’est donc aussi une puissance. On écrira donc : √x = xk, où k est une valeur à déterminer. Donc :
√(x2) = (x2)k
Nous avons trouvé plus haut que (x2)k doit être égal à x2k.
Par conséquent, x2k = x = x1.
Donc 2k = 1, ce qui nécessite k = 1/2.
On obtient donc :
√ = x1/2
On constate facilement que ce raisonnement se reproduit à l’identique si on remplce la racine carrée par la racine cubique, en remplaçant 2 par 3 :
La racine cubique est la puissance 1/3
De cette façon, on définit toutes les puissances de la forme 1/n.
Enfin, si on élève x1/n à la puissance p, on a
(x1/n)p qui d’après la même formule que précédemment, donne xp/n.
avec n et p entiers.
On a ainsi défini les puissances pour tous les nombres rationnels. On pourrait étendre cela encore pour définir la puissance par un nombre réel quelconque, puis pour un nombre complexe, mais c’est un petit peu plus compliqué. On admettra simplement que xn est défini pour toute valeur de n.
Après ce petit jeu, on peut donner une définition élémentaire du logarithme décimal :
Par définition, le logarithme de 10n est n, le nombre de zéros (nombre de zéros comme défini précédemment).
log(10n) = n
Si n est négatif (nombre inférieur à 1), le logarithme est négatif.
Remarque : c’est tout de même une drôle de fonction, définie seulement pour les puissances de 10 ! Il faudra remédier à ça…
Pour le savoir, on va déterminer une propriété simple de cette fonction.
Multiplions deux puissances de 10. Le résultat est encore une puissance de 10, dont le nombre de zéros est la somme des nombres de zéros des nombres multipliés. Ainsi, le produit de 1.000 par 10.000 est 10.000.000. 3 zéros et 4 zéros font 7 zéros. On entrevoit que multiplier les puissances de 10 revient à additionner les nombres de zéros.
Le nombre de zéros du produit est la somme des nombres de zéros.
Puisque les nombres de zéros sont les logarithmes, on a :
log(10n × 10p) = log(10n) + log(10p)
Ce qui pourrait se lire : le nombre de zéros de 10n multiplié par 10p est égal au nombre de zéros de 10n plus le nombre de zéros de 10p
Reprenant la formulation au-dessus, on peut dire :
le logarithme d’un produit de facteurs est la somme des logarithmes des facteurs
Ces trois dernières formulations ont le même sens.
Remplissons un petit tableau :
| 1.000 | × | 100 | = | 100.000 |
| 3 zéros | + | 2 zéros | = | 5 zéros |
En haut, on a la multiplication des nombres, en bas l’addition des nombres de zéros (c’est-à-dire des logarithmes). Elle met bien en lumière la correspondance entre la multiplication des nombres et l’addition de leurs logarithmes. Or il est facile d’ajouter des quantités ; par exemple des longueurs : il suffit de le mettre bout-à-bout.
Prenons un bout de bois de section carrée (une sorte de règle). Plaçons-le dans un support où il peut coulisser (goulotte pour installation électrique par exemple), et inscrivons tous les centimètres une nouvelle puissance de 10 sur la règle et sur son support. Il faut commencer à l’origine de la règle et du support par mettre 1 = 100.
En plaçant l’origine de la règle (1) en face de 104 sur le support par exemple ; en repérant 107 sur la règle, on constate que cette marque (sur la règle) se trouve en face d’une marque sur le support. Les graduations de la règle et du support correspondent aux logarithmes, c’est-à-dire aux nombres de zéros. En mettant règle et support bout-à-bout, on additionne les longueurs, donc les logarithmes. On doit alors s’attendre à ce que la marque en face de 107 sur le support soit 1011 ! Si vous faites l’expérience, vous pourrez le vérifier facilement.
Il est plus rapide (mais moins pratique) de tracer les repères sur deux feuilles de papier que l’on fait coulisser l’une par rapport à l’autre.
Ceci constitue un embryon de règle à calcul. Après un instant d’émerveillement (tout au moins, je l’espère), on lui reproche vite de ne pouvoir multiplier que les puissances de 10 ! Normal, si vous vous souvenez de la remarque faite plus haut, stipulant que notre fonction était bien parcellaire…
Il est donc temps, maintenant qu’on en voit une utilité, de l’approfondir.
Nous avonc été guidé, pour définir le logarithme, par des relations que nous avons prolongées (qui étaient vraies pour certaines puissances, et que nous avons forcées pour définir d’autres puissances qui, de ce fait, les respecteront aussi).
Nous allons procéder de même, en utilisant la relation fondamentale des logarithmes que nous avons trouvée plus haut, à savoir :
log(10n × 10p) = log(10n) + log(10p)
Puisque nous voulons l’élargir à des nombres qui ne seront pas des puissances de 10, nous allons remplacer les puissances de 10 dans son expression par des lettres a et b, représentant maintenant des nombres quelconques (une même puissance remplacée par une même lettre, bien sûr).
log(a × b) = log(a) + log(b)
Si vous fixez a = 10n et b = 10p, vous retrouvez bien la forme de départ, ce qui prouve que cette nouvelle écriture en est une généralisation. Elle est même plus facile à lire !
Adoptant cette relation, on peut déterminer le log de n’importe quelle puissance :
log(x2) = log (x × x) = log(x) + log(x) = 2 log(x)
log(x2) = 2 log (x)
Si on veut connaître le log d’un cube (puissance 3), il suffit de remarquer que x3 = x × x2.
Alors, log(x3) = log(x × x2) = log(x) + log(x2) = log (x) + 2 log(x) = 3 log(x).
En répétant ce procédé, on arrive à :
log(xn) = n log(x)
On pourrait pareillement montrer que la formule est valable pour les puissances négatives.
Cette formule pour le carré permet de placer une nouvelle marque sur la règle. Soit x, la racine carrée de 10. On a donc x2 = 10. Donc log(x2) = 1.
En appliquant la formule, log(x2) = 2 log(x). Donc 2 log(x) = 1, et log(x) = 1/2 !
La racine carrée de 10 vaut à peu près 3,16 et donc log(3,16) = 0,5. On peut ajouter sur la règle une graduation exactement au milieu entre 1 et 10, que l’on désignera par 3,16…
Par des techniques analogues, on pourrait construire le logarithme de n’importe que nombre. Mais il y a des méthodes plus efficaces, car plus régulières pour y parvenir.
Choisissons une valeur x. Elever 10 à la puissance x donne 10x. Par la définition que nous avons adoptée, prendre le logarithme de ce nombre donne log(10x) = x.
Partant de x, lui appliquant la fonction puissance de 10; puis la fonction logarithme décimal, nous retrouvons x… Comme si nous n’avions rien fait. Autrement dit, l’application successive de ces deux fonctions est neutre, et ceci ne dépend pas de x ! Comme par exemple multiplier par 2, puis diviser le résultat par 2. Pour cette raison, on dit que ces deux fonctions sont inverses l’une de l’autre. Cette propriété et souvent fort utile dans les calculs.
Notre vue nous montre des éclairements plus ou moins forts. Pour les étoiles, on en voit de très brillantes et d’autres beaucoup moins. Les Anciens les ont classées par grandeur, les étoiles de première grandeur étant les plus brillantes, celles de sixième grandeur les plus faibles. Cette notion était obtenue par l’observation visuelle bien sûr, et dépendait des propriétés de l’œil humain. Lorsqu’on a pu mesurer l’éclat d’une étoile avec un appareil qui détermine l’intensité lumineuse reçue, on s’est aperçu qu’entre une étoile de magnitude 1 et une autre de magnitude 2, il y avait un rapport d’énergie de 2,5. Si donc l’énergie reçue d’une étoile de magnitude 6 est e0, l’énergie reçue d’une étoile de magnitude 5 est 2,5 e0 ; celle d’une étoile de magnitude 4 sera 2,52 e0 ; d’une magnitude 3 : 2,53 e0 etc. Les énergies se multiplient là où les magnitudes s’additionnent ; on retrouve la propriété des logarithmes, ce qui justifie la formule m - M = 5 log d - 5.
Parce que c’est la fonction la plus simple à définir de façon intuitive, nous avons présenté le logarithme décimal (construit sur les puissances de 10). Mais on pourrait faire de même pour n’importe quel entier, par exemple 2. On obtiendrait ainsi le logarithme binaire (à base 2, le décimal étant dit à base 10).
Il n’est même pas obligatoire de prendre une base entière… On peut par exemple choisir pour base le nombre e = 2,7182818284590452353602874… Il semble bien tordu ! Pourquoi avoir choisi celui-là ? La raison est un peu délicate à donner ici, mais pour mémoire : ce choix définit pour la fonction logarithme, la dérivée la plus simple (c’est la fonction 1/x).
Pour cette présentation qui se veut intuitive des logarithmes, il vaut mieux en rester là.
Pour sourire un peu, on a défini deux nombres assez grands, le gogol et le gogolplex. Inutile de donner les valeurs correspondantes, vous pourrez les écrire facilement, n’est-ce pas ?
log(gogol) = 100
log(log(gogolplex)) = 100
---=OO=---