Historique de Marseille
| liens |
le 18/08/17
| ��L’actualité du LAM | ��Le cours à l’Observatoire Historique de Marseille |
| �� Mis à jour le 18/08/17 |
||||
| �� Relativité Restreinte | |||||||
Les objets de notre perception impliquent invariablement temps et lieu ensemble.
Personne n’a jamais observé de lieu, sauf en un instant donné,
ni de temps, sauf en un endroit précis.
Minkowski
Table des matières
1.1 Justification
1.2 Principe de Relativité
2 La lumière
2.1 L’éther
2.2 Vitesse de la lumière
2.3 Expérience de Fizeau
2.4 Expérience de Michelson-Morlay
2.5 L’électromagnétisme
2.6 Observateurs galiléens
2.7 Synthèse
2.8 But de la Relativité Restreinte
3 Relativité du temps
3.1 Notation
3.2 Automobile de Poincaré
3.3 Dilatation du temps
3.4 Autre explication
3.5 Horloges
4 L’espace-temps
4.1 Défaut de la Relativité Galiléenne
4.2 Transformation de Lorentz-Poincaré
4.3 Vie du muon
5 Où l’on retrouve le Théorème de Pythagore
5.1 Invariant relativiste
5.2 Représentation
5.3 Cônes de lumière
5.4 Ligne d’univers
5.5 Addition des vitesses
6 Conséquences
6.1 Non simultanéité
6.2 Contraction des longueurs
6.3 Application
6.3 La masse en Relativité
6.4 Relation fondamentale de la dynamique
6.5 L’énergie de masse d’une particule
6.6 Formalisme
7 Un peu d’histoire
8 Résumé
La théorie de la Relativité Restreinte à été publiée en 1905 par Albert Einstein, et la légende veut qu’il l’ait imaginée entièrement seul. Ce n’est pourtant pas le cas, et des travaux bien antérieurs l’ont précédée. Tout d’abord, les travaux de Henri Poincaré et Hendrik Lorentz sur la transformation des coordonnées, qui ont déjà amené la notion d’espace-temps. Ensuite, l’œuvre d’Henri Poincaré, qui a publié dès 1902 une version de la Relativité bien avancée. Le travail de Poincaré était une œuvre de mathématicien, et Einstein lui a ajouté l’interprétation physique indispensable. Il ne faut pas oublier qu’Einstein était un théoricien et qu’il a exercé son intuition sur la façon dont la Nature doit fonctionner. Une fois son opinion faite, il cherchait le moyen de la transposer dans une théorie, et en général, celle-ci lui donnait raison.
Pourquoi a-t-on remis en question la Relativité Galiléenne, alors que toutes les expériences de Mécanique étaient si bien expliquées ?
Rappellons que la Mécanique Céleste s’est développée au cours du XVIIe siècle, et que ses performances sont exceptionnelles ! Elles ont permis de prédire les éclipses avec une précision de quelques secondes (la théorie de la Lune sera améliorée par Brown en 1930). Alors, pourquoi changer une équipe qui gagne ?
Le problème n’est pas venu de la Mécanique, mais de l’Electricité. Plus précisément, de la théorie de l’Electromagnétisme achevée par Maxwell.
Le texte qui suit n’est pas un cours de Relativité Restreinte. Son but est de montrer comment la Relativité résoud les problèmes posés par les théories antérieures, et comment elle s’est développée.
La Relativité Galiléenne prend en compte les référentiels galiléens, et impose que les lois de la Mécanique soient invariantes par la transformation de Galilée (lorsque les vitesses sont petites devant celle de la lumière, mais ceci n’est pas indiqué, et n’apparaîtra que plus tard comme un défaut de la théorie).
La Relativité Restreinte conserve les référentiels galiléens, mais généralise en levant la restriction sur les vitesses, et en imposant l’invariance des lois de l’électromagnétisme. Elle impose donc l’invariance de toutes les lois de la Physique dans la transformation de Lorentz-Poincaré (qui remplace la transformation de Galilée).
| Remarque : | La Relativité Restreinte se limite aux référentiels galiléens. |
| La Relativité Générale englobera tous les référentiels. |
La lumière étant une onde électromagnétique, voyons ce qu’elle nous réserve. La lumière est une onde, c’est une affaire entendue. Après avoir longtemps hésité entre une théorie corpusculaire (déjà les grecs…) et une théorie ondulatoire, les physiciens se sont laissés convaincre par les expériences de diffraction et d’interférences, que seules les ondes pouvaient expliquer. Donc, la lumière est une onde. Une onde se propage dans un milieu matériel ! (pensez au son, qui est une variation de pression ; heureusement il ne se propage pas dans le vide, sans quoi le Soleil nous ferait un drôle de vacarme).
Mais la lumière qui nous parvient du Soleil se propage dans le vide. Comment la lumière peut-elle se propager sans milieu matériel ?
Pour contourner cette difficulté, les physiciens ont imaginé l’existence d’un milieu qui baignerait tout l’espace, vide ou non, et dans lequel la lumière se propagerait ; c’est un milieu ad-hoc qu’ils ont nommé éther. Tous les phénomènes que l’on considère en physique sont des phénomènes locaux ! Leur distance spatiale et temporelle est petite. Par contre, la notion d’éther est une notion globale.
Le problème était alors de le mettre en évidence, et d’en définir les propriétés exactes (par rapport à la matière en particulier).
L’éther, s’il existait, constituerait un référentiel absolu, par rapport auquel on pourrait déterminer tous les mouvements. Le repos par rapport à l’éther serait envisageable, contrairement à ce qu’on a dit au sujet de la Relativité Galiléenne. Mais l’éther n’étant pas directement accessible (on ne peut y poser un repère), il n’y a pas de contradiction dans la théorie.
La lumière pose un problème tout à fait particulier. La Mécanique Classique admettait les interactions à distance instantanées (la gravitation en particulier est une force ne dépendant pas du temps pour sa transmission, mais attention, gravitation et lumière ne sont pas la même chose). Par conséquent, dans la physique classique, la lumière se propage instantanément. Or ceci est faux. La vitesse de la lumière est très grande, mais finie. La première démonstration en a été donnée par Römer, qui a expliqué une erreur périodique entre les positions calculées et mesurées des satellites de Jupiter (sur les phénomènes remarquables que sont leurs éclipses). La période de cette erreur était égale à la révolution synodique de la planète, donc elle était liée aux mouvements combinés de Jupiter et de la Terre. Römer a montré qu’il fallait tenir compte du temps que met la lumière pour nous parvenir, selon que Jupiter est en opposition ou en conjonction, la distance changeant de 300 millions de km entre ces deux points. Si la vitesse de la lumière est finie, l’erreur s’explique par la différence de temps pour parcourir un trajet plus ou moins long. Römer avait trouvé une vitesse de l’ordre de 200.000 km s-1, ce qui est déjà très bien étant données les difficultés de la méthode. Remarquez que cette première mesure a utilisé une distance de plusieurs centaines de millions de kilomètres pour mettre cet effet en évidence.
Par la suite, Foucault a réalisé un montage permettant de mesurer la vitesse de la lumière sur une distance faible (quelques kilomètres). Puis des méthodes électriques ont été utilisées, avec une bien meilleure précision (la vitesse de la lumière intervient dans les équations de l’électromagnétisme, puisque la lumière est un phénomène électromagnétique).
Ces expériences mesuraient la vitesse de la lumière dans le vide (Römer) puis dans l’air (Foucault) ; les mesures électromagnétiques donnent la vitesse dans le vide, celle qui intervient dans les équations de l’électromagnétisme.
Ensuite, de nombreuses expériences, dont celles, célèbres, de Fizeau et de Michelson-Morlay, ont prouvé que la vitesse de la lumière est la même pour tous les observateurs galiléens, que ceux-ci soient au repos ou en mouvement. Les physiciens se sont ensuite tournés vers les phénomènes fins, liés aux conditions de la mesure.
L’expérience a consisté à mesurer la différence de vitesse de la lumière, lorsque l’éther dans lequel elle se déplace est entraîné par un milieu matériel (on ne pensait pas que l’eau elle-même entraînerait la lumière).
Fizeau a envisagé de faire passer le rayon lumineux dans un courant d’eau, mais pour mettre en évidence une différence forcément très faible (sinon elle aurait été mise en évidence bien avant), il fallait produire des interférences, phénomène extrêmement sensible. Pour cela, Fizeau faisait passer le rayon lumineux deux fois dans un courant d’eau, grâce à une lame semi-réfléchissante :
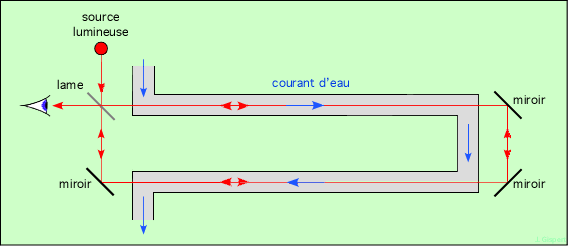
L’expérience a donné un résultat, sous la forme d’une formule empirique, qui n’est pas en accord avec l’addition des vitesses de la Mécanique Classique. Par contre, il sera parfaitement expliqué par la Relativité Restreinte, car il constitue une approximation au premier ordre de la formule relativiste d’addition des vitesses. Pour l’instant, c’est donc un accroc dans la théorie en usage, mais ce sera aussi une justification de la Relativité.
L’expérience de Michelson et Morlay est la plus célèbre des expériences de cette catégorie, et celle qui a emporté l’assentiment des physiciens.
Si la lumière se propage dans l’éther, étant donné que la Terre traverse celui-ci à 30 km s-1, la vitesse de la lumière doit être plus grande dans la direction du mouvement que dans la direction perpendiculaire. L’expérience consiste à lancer un rayon lumineux vers une lame semi-réfléchissante. Un partie du rayon, figurée en rouge, se réfléchit sur la lame, puis sur le miroir, revient vers la lame et la traverse pour atteindre l’observateur (bien sûr, une partie du rayon se réfléchit sur la lame au retour et revient vers la source ; cette partie est perdue). Une autre partie de la lumière émise (représentée en bleu) traverse la lame, se réfléchit sur le second miroir, puis se réfléchit sur la lame au retour (une autre partie traverse…). L’observateur reçoit donc deux rayons différents, émis par une même source, mais ayant parcouru des chemins différents, à une vitesse différente si l’on en croit la physique classique (addition des vitesses). Lors de l’aller-retour dans la direction du mouvement (de la Terre), la perte dans un sens ne compense pas le gain dans l’autre, et le résultat classique est un déphasage du rayon bleu par rapport au rayon rouge.
Ce déphasage doit être observé, il est nettement au-dessus des erreurs de mesure.
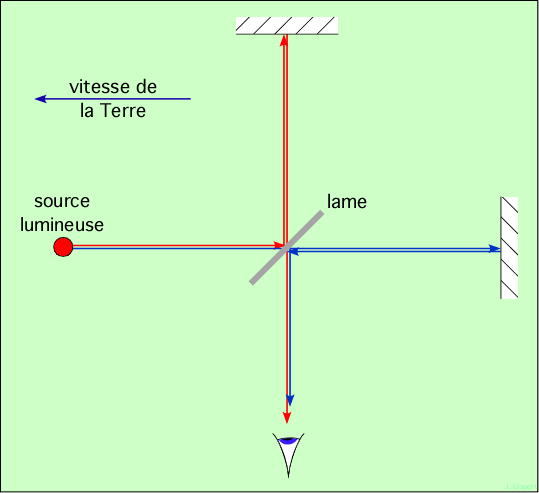
Et l’on n’a rien vu ! L’expérience refaite maintes fois a été têtue, elle a toujours donné le même résultat, négatif… Il n’y a pas d’entraînement de la lumière par l’éther. Et comme l’éther a été imaginé pour porter la lumière, il n’a plus de raisons d’être ! Exit l’éther …
Cette expérience a montré donc qu’il n’existe pas de référentiel absolu (l’éther). Elle a aussi montré que la vitesse de la lumière est indépendante de la vitesse de déplacement de la Terre : c + 30 km s-1 = c ! Cette équation, mathémtiquement fausse mais significative, met en défaut l’addition classique.
L’électromagnétisme est défini par un jeu de quatre équations (équations de Maxwell) qui permettent de décrire tous les phénomènes concernant l’électricité et le magnétisme. Or un petit calcul à partir de ces équations indique la formation d’ondes électromagnétiques, dont la vitesse de propagation est donnée par :
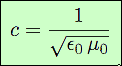
Les deux termes ε0 et μ0 sont les deux constantes fondamentales de l’électricité et du magnétisme. Par conséquent, la vitesse des ondes électromagnétiques qui en découle est aussi une constante. Le calcul montre qu’elle est égale à la vitesse de la lumière. Il a été prouvé par ailleurs que la lumière est bien cette onde électromagnétique-là. Donc la vitesse de la lumière, déduite de l’électromagnétisme, est bien une constante.
Sans considérer les ondes, le simple examen de la quatrième de ces équations, l’équation de Maxwell-Ampère, suffit pour prouver que la vitesse de la lumière est finie. En effet, elle s’écrit :
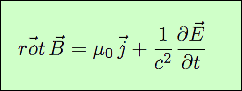
Si c est infini, le terme dE / dt a son coefficient nul. Il disparaît donc, ce que contredit l’expérience. Et dans ce cas, les équations de Maxwell seraient invariantes dans la transformation de Galilée.
Tout ceci fait un ensemble de problèmes qui affectent la théorie, et qui appellent à définir une sur-théorie, englobant celle-ci et résolvant ces problèmes. Ce sera la Relativité Restreinte.
Ce qui a été dit à propos de la Relativité Galiléenne n’a pas à être remis en cause : l’équivalence des référentiels galiléens est conservée.
Pour synthétiser cette introduction, nous pouvons noter que :
Regardons le résultat essentiel de la Relativité Galiléenne à la lumière (c’est le cas de le dire) de l’invariance de c. Reprenons pour cela le simple problème du train, mais en remplaçant le voyageur par un rayon lumineux issu d’une lampe fixée au wagon, et dirigée vers l’avant. Lorsque cette lampe est allumée, à quelle vitesse l’observateur situé sur le quai voit-il se déplacer le rayon lumineux ?
La réponse est simple. On applique la loi d’addition des vitesses vq = vLt + Vt, où vLt est la vitesse de la lumière dans le référentiel du train, Vt est la vitesse du train par rapport au quai, et vq la vitesse du rayon lumineux par rapport au quai. Dans l’exposé du problème nous avions Vt = 100 km h-1 ; vLt = c, donc :
vq = c + 100 km h-1
Inutile de faire le calcul, il est évident que le résultat est strictement supérieur à c. La conséquence de l’addition des vitesses est que le rayon lumineux se déplace à une vitesse supérieure à c par rapport au quai.
Nous venons de voir que ce résultat est en contradiction flagrante avec l’expérience. Et c’est toujours l’expérience qui a raison contre la théorie ! Par conséquent, la loi galiléenne d’addition des vitesses est fausse.
La Mécanique Classique ne peut donc s’étendre hors de son domaine des petites vitesses, puisque la vitesse de la lumière est la même dans tous les référentiels (ce qui implique que l’addition des vitesses n’est pas réelle). Voilà les idées de base à partir desquelles la Relativité a été bâtie. Remarquez qu’elles sont particulièrement solides.
De nombreux physiciens ont cherché à résoudre le problème. Abandonner l’addition des vitesses signifie la remplacer par une autre formule qui donnerait les mêmes résultats à petite vitesse, mais qui limiterait toujours à la vitesse de la lumière. La recherche de cette formule est un problème mathématique, qui a de nombreuses solutions. Il a été résolu par Poincaré et Lorentz, mais prenons les choses par le début.
Dans ce qui suit, on notera les coordonnées dans le référentiel mobile avec des primes : x′, y′, z′, t′, alors que les coordonnées dans le référentiel fixe n’en auront pas. Cette convention permet de distinguer immédiatement dans quel référentiel une variable se place.
Si nous partons, comme Poincaré et Einstein, de l’invariance de la vitesse de la lumière dans tous les référentiels, on peut comprendre que le temps ne puisse être absolu !
Prenons une source lumineuse et un miroir, ce dernier bien en face de la lampe. Plaçons-les verticalement dans une voiture à l’arrêt (figure 1.1).
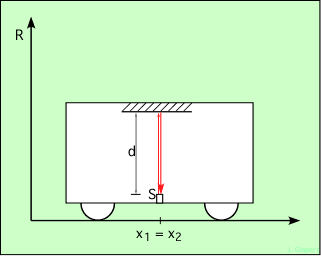
Figure 1.1 : Le rayon dans le référentiel de la voiture
Un rayon lumineux issu de la lampe va se réfléchir sur le miroir, et revenir à la lampe. Si d est la distance entre la lampe et le miroir, le rayon lumineux (en rouge) a parcouru la distance 2 d, à la vitesse c évidemment, donc dans le temps t = 2 d / c.
Vu du bord de la route (figure 1.2), associé au référentiel R′, dans lequel la voiture est en mouvement à la vitesse V, le signal lumineux est émis lorsque la voiture est en x′1, et reçu par la lampe, après réflexion sur le miroir, lorsque la voiture est en x′2.
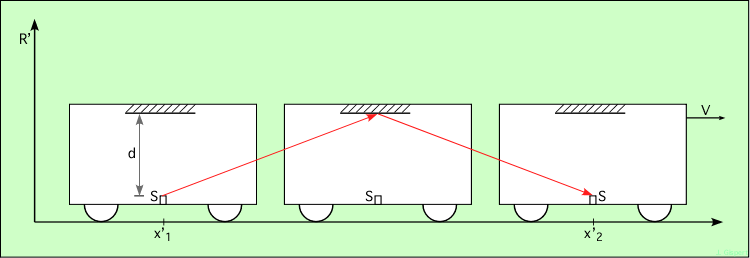
Figure 1.2 : Le rayon vu du bord de la route
Lorsque le signal atteint le miroir, la voiture est au milieu de ce parcours. Le trajet du signal (en rouge), vu de la route, est donc plus long que vu de la voiture. Or il est parcouru à la même vitesse c, puisque la lumière se déplace à cette vitesse-là dans tous les référentiels. Donc, puisque le trajet est plus long, et parcouru à la même vitesse, le temps de parcours doit être plus long. Le temps mesuré depuis le bord de la route est par conséquent supérieur au temps propre, mesuré dans la voiture.
La mesure du temps dépend donc de la vitesse du référentiel en mouvement. Le temps n’est plus absolu comme le supposait la Mécanique Classique (la Relativité Galiléenne).
Chaque observateur possède son temps propre, celui du référentiel dans lequel il est au repos.
Précisons le lien : on a constaté expérimentalement que la vitesse de la lumière était la même dans tous les référentiels galiléens. Ceci implique que le temps mesuré par différents observateurs est différent.
Schématisons les deux référentiels de la voiture :
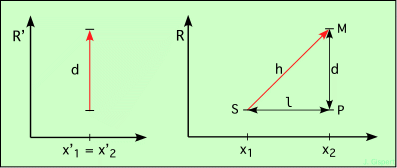
Le dessin de gauche montre le référentiel de la voiture. Il représente le seul rayon qui va de la source au miroir (moitié du trajet total). Le dessin de droite illustre la même situation vue de la route. Le rayon lumineux est diagonal, son trajet est de longueur h, la voiture s’est déplacée de la longueur l, et le miroir est toujours éloigné de d de la source.
Dans le tableau ci-dessous, Δ représente une différence. Δt est la différence entre deux temps, donc une durée.
| R′ référentiel de la voiture | R référentiel de la route |
|---|---|
| Δt′ = temps pour parcourir d de la source au miroir, à la vitesse c | Δt temps pour parcourir h de la source au miroir, à la vitesse c |
| Δt′ = t′2 - t′1 = heure de réception - heure d’émission dans R′ | Δt = t2 - t1 = heure de réception - heure d’émission dans R |
| d = c Δt′ | h = c Δt |
| l : distance parcoure par la voiture pendant le temps Δt, à la vitesse v | |
| l = v Δt | |
| triangle SPM est rectangle, Pythagore : h2 = l2 + d2 |
Reportons dans la dernière égalité les valeurs de h, l et d trouvées plus haut : (c Δt)2 = (v Δt)2 + (c Δt′)2 c’est une relation entre Δt et Δt′.
c2 Δt2 = v2 Δt2 + c2 Δt′2⇒c2 Δt2 - v2 Δt2 = c2 Δt′2
⇒(c2 - v2) Δt2 = c2 Δt′2⇒Δt2 = c2 Δt′2 / (c2 - v2)
et enfin, divisant par c2 à droite : Δt2 = Δt′2 / (1 - v2 / c2)
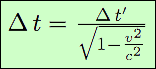
Cette mesure de la dilatation du temps, que nous venons d’obtenir facilement sur un exemple, est un cas particulier de la transformation générale que nous verrons plus loin. Mais cette dernière se détermine sur d’autres principes. On pose :

et donc :
Remarque 1
Vous pouvez constater que la mesure du temps dépend du trajet parcouru par la voiture, donc de la position de la voiture ! Par conséquent, espace et temps sont mélangés… Le temps t′ mesuré depuis le bord de la route, dépend à la fois du temps t mesuré dans la voiture, et de la distance d entre la source et le miroir : t′ = F(d,t).
Remarque 2
Ce phénomène a été considérablement amplifié sur le schéma. En effet, si la distance d vaut 1,5 m, la lumière mettra pour parcourir les 3 m de l’aller-retour, un temps propre t = 3 m / 300.000 km s-1 = 10-8 s, soit 10 milliardièmes de seconde. Pendant ce temps, la voiture, roulant à 100 km h-1, aura parcouru l’énorme distance de… 0,28 millièmes de millimètre ! Autant dire que les 3 dessins de la voiture, à droite, devraient être superposés sans possibilité de les distinguer. C’est pourquoi, avec de petites vitesses, il est absolument impossible de ressentir les effets de la Relativité. Ceci explique qu’on ne l’ait pas découverte plus tôt.Remarque 3Rêvons un instant que la voiture puisse se déplacer à la vitesse de la lumière (attention aux radars…). Pendant que le rayon lumineux atteint le miroir, la voiture aura parcouru 1,5 m (la même distance, puisqu’elle va à la même vitesse). Il en est de même pour le rayon réfléchi. Au total la voiture aura avancé de 3 m pendant l’aller-retour du rayon. Donc, l’angle des rayons rouges est au maximum droit contre le miroir ; dans tous les cas réels (V < c), il est aigu. Sur le dessin, pour la lisibilité, il a été représenté obtus…
A partir de cette expérience, on peut obtenir très facilement la relation entre les deux référentiels (transformation de Lorentz-Poincaré).
La relativité du temps est un phénomène de perspective :
le temps dépend du point de vue sous lequel on le mesure.
Une fusée s’éloigne à une vitesse proche de la vitesse de la lumière. A chaque seconde de son horloge, elle envoi un signal vers la Terre. Pour mesurer le temps qui s’écoule dans la fusée depuis la Terre, on utilise ces signaux. Mais il est évident qu’entre deux signaux successifs, la fusée à parcouru une distance non négligeable, et que le signal aura d’autant plus de trajet à parcourir pour parvenir sur Terre. Mais pour tenter un calcul direct, il faudrait bien prendre garde à ne pas mélanger les référentiels, ce qui n’est pas si simple… Conservons donc cette image comme une indication qualitative, et non quantitative.
Evidemment, si la Terre envoi des signaux vers la fusée, le même allongement de la distance est réalisé, et donc le mouvement est vu ralenti pareillement. Cet allongement du temps observé est symétrique.
Reprenons la voiture dans son référentiel, et imaginons que, lorsque le rayon revient à l’émetteur, il déclenche ainsi un second éclair. L’arrivée du second en déclenchera un troisième, et ainsi de suite. Les événements « arrivée d’un éclair » peuvent être considérés comme des tops d’horloge : notre système lumineux est une horloge. Dans la voiture, nous pouvons parfaitement l’utiliser pour mesurer le temps.
Sur le bord de la route, nous pouvons installer une horloge identique : les deux horloges fonctionnent pareillement, chacune dans son référentiel. Etant identiques, elles ont le même temps propre. Mais vu du bord de la route, le trajet aller-retour effectué par le rayon lumineux de l’horloge embarquée fait un chemin plus long que celui fait dans l’horloge à terre. Par conséquent, le temps mesuré, du bord de la route, sur l’horloge embarquée, est plus long que celui mesuré sur l’horloge fixe. C’est-à-dire que les passagers de la voiture (et la voiture elle-même) vieillissent moins vite !
Puisque la mesure du temps est relative à la position de l’observateur, elle dépend, nous l’avons vu, à la fois des coordonnées d’espace et de temps de l’autre référentiel. Ces quatre coordonnées sont donc indissociables, et constituent l’espace-temps. Ce dernier est un espace mathématique, qui possède des propriétés très semblables à notre espace habituel à 3 dimensions, mais il en a 4. On peut y définir une longueur, un volume… Ce sont simplement des fonctions mathématiques ayant les mêmes propriétés que leurs correspondantes dans l’espace à trois dimensions.
Nous avons vu plus haut que l’addition des vitesses de la Relativité Galiléenne ne s’applique pas lorque les vitesses (une d’entre elles au moins) sont proches de la vitesse de la lumière. Comment résoudre ce problème, qui s’est posé au début du XXe siècle ? Soit la notion de vitesse de la lumière indépendante du référentiel était fausse, soit c’était la loi d’addition des vitesses. Toutes les expériences qui ont été faites ayant conclu à l’invariance de la vitesse de la lumière, il ne restait plus qu’à admettre que la formule d’addition des vitesses ne pouvait s’appliquer lorsque les vitesses sont proches de celle de la lumière. Bien sûr, la physique classique ne pouvait être remise en cause dans le domaine de vitesses (très petites devant la vitesse de la lumière) où elle avait été définie. Il fallait donc trouver une nouvelle loi de composition des vitesses, qui corresponde avec la loi d’addition classique pour les vitesses faibles, mais qui ne dépasse jamais la vitesse de la lumière.
Puisque l’addition des vitesses découle de la transformation de Galilée, celle-ci n’est plus valable. Il faut lui substituer une forme plus complexe. C’est par là que la recherche a été faite.
Terminologie : On parle de phénomène relativiste lorsque les vitesses mises en jeu sont comparables avec celles de la lumière ; dans le cas contraire, il est dit non relativiste. Le domaine non relativiste est donc celui de la Mécanique Classique. L’écart entre les résultats classiques et relativistes y est insignifiant.
Ce postulat d’invariance de la vitesse de la lumière n’est donc pas nécessaire pour construire la Relativité Restreinte, et la transformation de Lorentz-Poincaré peut se démontrer en dehors de lui. Au contraire, l’invariance de la vitesse de la lumière apparaîtra comme une conséquence de cette transformation, conséquence qui s’applique à toutes les interactions, éliminant ainsi le problème.
Jean-Marc Lévy-Leblond a donné une démonstration qui produit la transformation de Lorentz-Poincaré en utilisant l’homogénéité et l’isotropie de l’espace-temps, ainsi que l’équivalence des référentiels galiléens. Cette démonstration met en évidence une vitesse limite, sans en donner la valeur. Cette vitesse limite peut être assimilée à la vitesse de la lumière, mais pourrait aussi lui être supérieure. En fait, une particule ne peut atteindre cette vitesse limite que si sa masse est rigoureusement nulle. Ceci sera expliqué plus loin. La masse du photon est réputée nulle ; si ceci est exact (et non approché) alors la vitesse limite est bien c. Mais toute la théorie resterait valable, même s’il y avait une différence minime entre la vitesse limite et c. Et Louis de Broglie a toujours soutenu que le photon possède une masse, extrêmement petite, mais non nulle. Si c’était le cas, sa vitesse c serait très légèrement inférieure à la vitesse limite.
La vitesse limite devenant ainsi une propriété de l’espace-temps, il est naturel que tout ce qui se passe dans l’espace-temps en soit affecté, et par conséquent que toutes les interactions subissent la même limitation.
La transformation obtenue est la suivante :
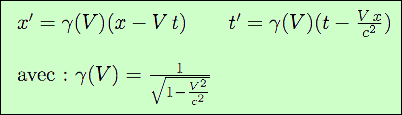
On reconnait le facteur γ qu’on avait trouvé dans le cas particulier de l’automobile de Poincaré.
Remarque 1 : si c → ∞, v2 / c2 → 0, et donc γ(V) = 1, et V x / c2 → 0. D’où x′ → x - V t, et t′ → t (transformation de Galilée). La transformation de Galilée est donc compatible avec celle de Lorentz-Poincaré, lorsque la vitesse limite est infinie (ce qui revient à dire qu’il n’y a pas de vitesse limite, ce qui est le paradigme de la Mécanique Classique). La vitesse de la lumière c étant très élevée (300.000 km s-1), il est impossible de distinguer entre les deux transformations, tant qu’on ne fait que des expériences à faible vitesse.
Remarque 2 : la transformation de Lorentz-Poincaré donnée ci-dessus est simplifiée (on la dit parfois spéciale), en ce sens que l’on n’a considéré qu’un seul axe d’espace pour le référentiel, cet axe étant parallèle à la vitesse du référentiel. La transformation de Lorentz-Poincaré complète comprend les axes y et z, qui sont inchangés par le mouvement. Donc y′ = y et z′ = z. Enfin, si on considère le référentiel dans une orientation quelconque par rapport à la vitesse, il suffira de faire une rotation pour obtenir les formules à appliquer. L’effet relativiste s’applique dans la direction de la vitesse, il est nul dans les directions perpendiculaires. Si le référentiel n’est pas aligné avec la vitesse, l’effet se réparti éventuellement sur les trois axes, par projection.
Remarque 3 : La construction actuelle de cette transformation s’appuie sur l’homogénéité de l’espace-temps, et sur l’équivalence des observateurs galiléens. Cette dernière implique, mathématiquement, que les transformations constituent un groupe (ensemble muni d’une loi de composition interne associative, possédant un élément neutre et un opposé). Toute transformation doit posséder une inverse (le point de vue de l’autre référentiel), et il doit exister une transformation identique (i.e. qui ne change rien), c’est la transformation à vitesse nulle. Ces deux propriétés mathématiques permettent de déterminer une transformation qui contient une constante dont la dimension est une vitesse. Appellons Χ cette vitesse ; la transformation trouvée est la transformation de Lorentz-Poincaré dans laquelle c est remplacé par Χ. Cette constante, déterminée par les propriétés de l’espace-temps, totalement en dehors de la vitesse de la lumière, apparaît en jouer le rôle. On peut les assimiler, si le photon a bien une masse strictement nulle. Sinon, la vitesse de la lumière serait très légèrement inférieure à cette constante. Le fait que ce soit une constante de structure de l’espace-temps explique clairement que toutes les interactions en soient affectées. C’est bien plus satisfaisant que de croire que les autres interactions se plient aux propriétés de la lumière (pourquoi pas la réciproque ?).
Importance de l’effet : Prenons par exemple une fusée se déplaçant à 8 km s-1 (vitesse de satellisation autour de la Terre). Entre le référentiel R lié à la Terre, et le référentiel R′ lié à la fusée, la transformation de Lorentz-Poincaré donne :
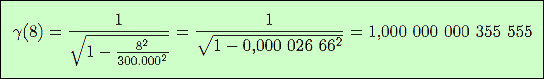
γ(V) = 1 à 3 10-10 près, soit 3 dix-milliardièmes ! Ceci est totalement non significatif. Même pour la vitesse d’une fusée, il n’est pas possible de distinguer entre les deux formules. Pour une vitesse de 30.000 km s-1, soit c / 10, l’écart n’est encore que de 5 millièmes… Pour envoyer une fusée sur Mars, la Mécanique Classique est totalement justifiée. A posteriori, on justifie également la Mécanique Céleste basée sur la loi de Newton. Cependant, cette loi de Newton sera prise en défaut lorsqu’on considérera des corps très denses, étoile à neutrons ou trou noir. Mais ceci est une autre histoire, qui concerne la Relativité Générale.
Linéarité : Les transformations de Lorentz-Poincaré sont linéaires par rapport aux longueurs et au temps. En effet, les coefficients γ(V), V et c sont indépendants de x et t, ce sont des constantes. Et donc, la transformation est de la forme :
![]()
Ceci a une conséquence importante : la mesure d’une longueur est de la même forme que celle d’une position. En effet, une longueur est la différence de deux positions : l = x2 - x1 = Δ x. En écrivant la transformation de Lorentz-Poincaré pour chacun des deux points x1 et x2, et en retranchant, on trouve :
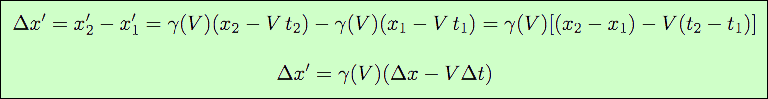
C’est-à-dire que, grâce à la linéarité, on peut remplacer dans la transformation de Lorentz-Poincaré, une position par une longueur, et un instant par une durée.
Le muon est un électron lourd (il a la même charge électrique, mais une masse 207 fois plus élevée). Etant plus lourd, le muon est instable, et se désintègre spontanément en un électron et deux neutrinos (conservation de la charge électrique et de la charge leptonique). Sa durée de vie, dans son référentiel, c’est-à-dire au repos, est de Δt′ = 2,2 µs. Les muons se déplacent à une vitesse très proche de celle de la lumière, V = 0,995 c. Donc, la distance qu’ils peuvent parcourir avant de se désintégrer, dans leur référentiel, est de Δx′ = c Δt′ = 300.000 km s-1 × 2,2 µs = 0,66 km = 660 m. Or les muons sont produits en abondance dans la haute atmosphère, par le rayonnement cosmique. Ces muons se déplacent vers le sol, et ne devraient parcourir que quelques 660 m en moyenne. Par conséquent, ils devraient être pratiquement inobservables au sol. Ce que contredit l’expérience !
Mais si on raisonne maintenant dans notre référentiel, lié au sol, on doit considérer le passage du référentiel lié à la particule, à celui lié au sol. L’un se déplace par rapport à l’autre à la vitesse V = 0,995 c, et le muon est immobile dans son référentiel. Le temps est multiplié par :
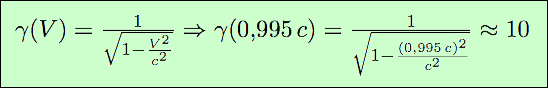
donc Δt = 10 Δt′, et puisque la vitesse est la même dans les deux référentiels, Δx = 10 Δx′ = 10 × 660 m = 6,6 km. Ceci en moyenne. C’est une valeur qui explique tout à fait la présence de muons d’origine cosmique à basse altitude. La transformation de Lorentz-Poincaré, clé de voûte de la Relativité Restreinte, permet donc de comprendre ce phénomène. Mais en retour, cette observation valide la théorie.
Tout le monde connait ce fameux théorème, qui donne la longueur de l’hypoténuse d’un triangle rectangle :
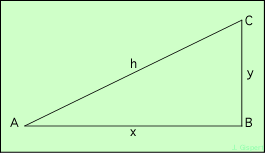
Le théorème de Pythagore permet de calculer l’hypoténuse h, à l’aide des côtés de l’angle droit x et y : h2 = x2 + y2.
Dans un référentiel à deux dimensions, on peut ainsi mesurer un segment quelconque AC :
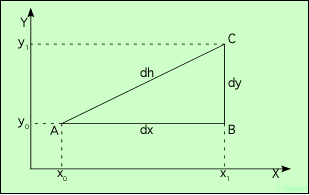
Les côtés sont maintenant notés dx = x1 - x0, et dy = y1 - y0. Par conséquent, l’application du théorème donne : dh2 = dx2 + dy2.
Pourquoi avoir nommé les côtés avec un d ? La notation utilisant d signifie différentielle, et représente une longueur infiniment petite (c’est la différence de deux positions infiniment voisines). Ceci parce que, sur une très petite longueur, on peut confondre un arc de courbe avec un petit segment de droite. Une courbe est ainsi décomposée en une succession de minuscules segments, c’est-à-dire par une ligne brisée qui lui ressemble énormément (et qui lui ressemble d’autant plus que le découpage est plus fin). Tout le calcul différentiel est basé sur ce principe, et la Relativité est une grande consommatrice de ce genre de calcul, parce qu’elle ne fixe pas les données dans l’absolu, mais relativement les unes aux autres.
Enfin, ce théorème se généralise immédiatement à trois dimensions (notre espace physique) : dh2 = dx2 + dy2 + dz2.
dh est la diagonale du parallélépipède de côtés dx, dy et dz, analogue de l’hypothénuse du triangle de Pythagore.
Considérons maintenant un photon, qui se déplace évidemment à la vitesse de la lumière. Comme on considère un déplacement infinitésimal, il se passe dans un temps lui aussi infinitésimal, que l’on note donc dt. Pendant ce temps dt, le photon parcours la distance dh = c dt. Donc : dh2 = dx2 + dy2 + dz2 = c2 dt2.
Faisant passer la somme centrale à droite du signe = on obtient une quantité nulle : c2 dt2 - dx2 - dy2 - dz2 = 0.
Cette équation est fondamentale, car elle représente le comportement d’un photon dans l’espace-temps (puisqu’elle le décrit en fonction des coordonnées d’espace et de temps). Peut-on la généraliser pour une particule non relativiste (à faible vitesse) ? Pendant le temps dt, la lumière parcourt toujours la longueur c dt, et la particule ne parcours qu’une longueur bien moindre, dx2 + dy2 + dz2. Par conséquent, c2 dt2 > dx2 + dy2 + dz2 ⇒ c2 dt2 - dx2 - dy2 - dz2 > 0.
On vient donc de trouver un terme qui représente le cheminement d’une particule, relativiste ou non, dans l’espace-temps. Si la particule se déplace à la vitesse de la lumière (particule de masse nulle), ce terme est nul ; sinon, il est positif. On le note ds2, et on l’appelle intervalle d’univers. Il est donc défini par : ds2 = c2 dt2 - dx2 - dy2 - dz2.
Remarquez que les signes des termes de temps et d’espace sont opposés. Certains auteurs définissent le ds2 en prenant la convention de signe opposée (le terme c2 dt2 négatif, les autres positifs, mais les termes dépendant de l’espace sont toujours de signe opposé au terme dépendant du temps).
Remarquez aussi que le premier terme c2 dt2 est le carré du produit c dt d’une vitesse par un temps. Une vitesse étant le rapport d’une distance sur un temps, c dt est une longueur. Donc le ds2 s’exprime en unités de longueur au carré.
Cette expression définit la Métrique de Minkowski :
Aucun signal ne peut se déplacer plus vite que la lumière. Donc, le ds2 d’une particule ne peut être que positif ou nul.
Remarque : la dénomination métrique est ici employée à tort. Une véritable métrique est une forme quadratique définie positive, ce qui n’est pas le cas ici (à cause des signes -). On devrait parler de pseudo-métrique, ou de forme Lorentzienne.
Le ds2 que nous venons de définir est un invariant relativiste, c’est-à-dire qu’il ne change pas de valeur si on passe d’un référentiel galiléen à un autre. Il est facile de le démontrer : on calcule c2 t′2 - x′2, et on y remplace t′ et x′ par les valeurs données par la transformation de Lorentz-Poincaré. On montre ainsi que : c2 t′2 - x′2 = c2 t2 - x2.
Cette invariance fait apparaître le ds2 comme le carré d’une longueur : lorsqu’on change de point de vue dans l’espace ordinaire à trois dimensions, la longueur d’une règle nous apparaît différente, mais pourtant elle ne l’est pas. Si on regarde la règle de face, on voit x = l, y = 0. Si on la tourne de 90°, on voit alors x = 0 et y = l. Mais la longueur
![]()
ne change pas !
Dans l’espace-temps, cette notion de longueur est plutôt celle de distance entre événements : la transformation de Lorentz-Poincaré change à la fois la mesure d’espace et la mesure de temps, mais la longueur qu’on en déduit, la distance entre les événements, ne varie pas. La transformation de Lorentz-Poincaré permet de faire de la géométrie dans l’espace-temps.
Remarquez aussi que la définition du ds2 est semblable au théorème de Pythagore. Celui-ci nous donne la longueur de l’hypoténuse, et c’est bien une longueur que nous avons définie ici, puisqu’elle est invariante.
Enfin, lorsqu’on fait tourner une règle dans notre espace à trois dimensions, elle ne change pas de longueur, mais nous la voyons en apparence de longueurs différentes. Dans l’espace-temps, on démontre aussi que la transformation de Lorentz-Poincaré est une rotation !
Pour bien comprendre la Relativité, il importe d’avoir une représentation intelligible de l’espace-temps. Il n’est pas question de nous tordre les méninges (qui le sont bien assez) pour arriver à conceptualiser un espace à 4 dimensions de manière simple, parce que notre expérience quotidienne se déroule dans un espace qui n’en a que trois. Alors, pour visualiser ce dont on parle, on aplatit le monde ! Cette méthode n’est d’ailleurs pas choquante, puisque c’est exactement ce que nous faisons lorsque nous prenons une photo : on capture une image du monde à trois dimensions sur une pellicule qui n’en a que deux, et lorsqu’on regarde la photo, on imagine la troisième dismension. Et lorsqu’on regarde le ciel, c’est bien une image à deux dimensions de l’espace que nous avons !
Qu’est-ce-qu’un film ? Une succession d’images fixes qui, projetées très rapidement l’une après l’autre, nous donne l’illusion de la continuité et du mouvement. Nous allons faire un film (figure 1.3) pour représenter l’espace-temps, réduit à deux dimensions.
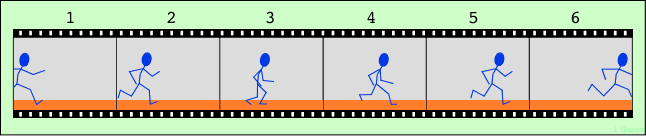
Figure 1.3 : Un petit film
Prenez la pellicule de votre film préféré. Dans ces conditions, l’axe vertical représente le temps, chacune des images étant séparée de la précédente par un vingt-cinquième de seconde. |
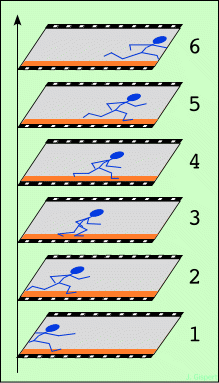 |
Effacez les images sur la pellicule, pour ne garder que les plans successifs, dans lesquels la scène se jouera. Voilà notre représentation de l’espace-temps. Tout phénomène physique peut donc s’y représenter par une sorte de film. Dans la réalité, l’espace physique étant de dimension 3, il faut par la pensée remplacer chaque plan par un volume. Mais c’est la seule difficulté, tout le reste étant inchangé.
Pour expliquer les cônes de lumière graphiquement, nous allons prendre la représentation de l’espace-temps étudiée au paragraphe 1.4.1. L’espace sera représenté par un plan horizontal quelconque, et le temps par l’axe vertical. Ainsi, tout plan horizontal représente l’espace, au temps correspondant à la coordonnée verticale.
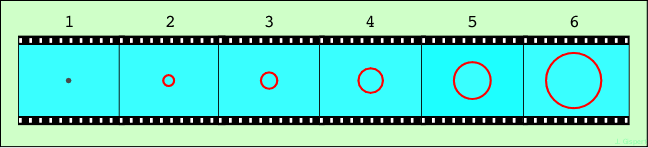
Figure 1.4 : des ronds dans l’eau
Filmons une pierre tombant dans la piscine (figure 1.4). Elle produit une onde qui se propage depuis le point de chute. Le film échantillonne les images toutes les 25 ms. C’est pourquoi il y a des trous entre deux images. Dans notre perception, c’est la persistance rétinienne qui les comble. En empilant les images, on obtient le dessin ci-contre L’axe vertical représente le temps, qui croît de bas en haut. Dans l’espace-temps, bien sûr, il y a continuité : on ne peut ici représenter que quelques images avec des trous entre elles. Imaginez que vous filmez avec une caméra ultra-rapide. Au lieu de prendre pour sujet la pierre dans la piscine, filmez une ampoule qui émet un éclair. Sur la première image, seule l’ampoule brille. Sur la seconde, elle s’est déjà éteinte, mais l’onde émise se trouve maintenant sur un petit cercle dont le rayon est r = c dt, dt étant le temps qui sépare les deux images. Sur la troisième, le cercle s’est agrandi de la même quantité c dt (puisque le temps qui sépare deux images est le même). |
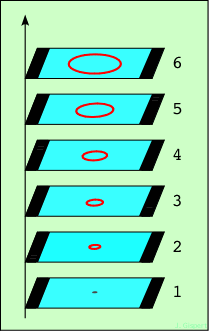 |
D’une image à l’autre, en montant, les cercles s’agrandissent donc régulièrement (vitesse de l’onde constante), et constituent un cône. Il ne nous reste qu’à expliciter un peu le dessin.
Considérons un point quelconque du temps présent, où se tient l’observateur O (ici et aujourd’hui). Dessinons l’axe du temps vertical passant par ce point (tout axe parallèle serait équivalent, celui-ci est simplement le plus pratique). Les cercles de couleur représentent une partie de l’espace à un instant donné : c’est l’ensemble des points dont la distance spatiale (habituelle) est inférieure à une certaine limite R(t), le rayon du cercle (on note R(t) parce que ce rayon dépend du temps).
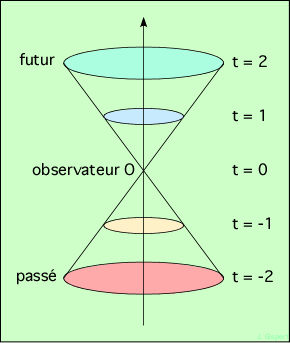
Supposons qu’une lampe soit allumée par l’observateur à t = 0 (ici et maintenant). Elle illumine l’espace dans toutes les directions. Les photons s’éloignent de l’observateur O horizontalement, puisqu’ils voyagent dans l’espace (restreint à deux dimensions). Mais le temps avance, donc les positions successives des rayons montent le long de l’axe du temps. Le cercle bleu représente donc la partie de l’espace qui sera baignée de lumière à t = 1, son rayon étant R(1) = c ; le vert à t = 2, de rayon R(2) = 2 c…
De même, au-dessous de l’observateur, on peut envisager de faire tourner le film à l’envers : descendre le long de l’axe du temps en-dessous de O consiste à remonter dans le passé. Puisque le temps va toujours vers le haut, on ne peut pas envoyer un signal vers le bas, mais on peut en recevoir : le cercle jaune contient tous les points de l’espace qui sont visibles par l’observateur, s’ils ont émis un signal depuis t = -1, puisqu’ils sont à une distance au plus égale à celle que peut parcourir la lumière pendant ce temps. Le cercle rouge enfin contient les points visibles qui ont émis le signal depuis t = -2.
La lumière se comporte exactement comme les ronds dans l’eau. C’est une onde qui se propage à une vitesse particulière. Si nous n’en sommes pas conscients, c’est que la vitesse de la lumière est vraiment trop grande pour nos sens. Pour inonder une pièce de 3 m lorsqu’on tourne l’interrupteur, il lui faut seulement 10-13 s, soit un dix millième de milliardième de seconde…
Qu’en est-il des points à l’extérieur du cône ? Pour un temps t donné (par exemple t = 1), les points qui ont eu le temps d’envoyer un signal depuis t = 0 sont dans le cercle de rayon ct. Ceux qui sont à l’extérieur de ce cercle (P par exemple) n’ont pas pu transmettre un signal depuis t = 0 (ils ont pu en envoyer, mais ceux-ci ne sont pas encore parvenus). Ils sont en-dehors de l’horizon… Mais si on attend t = 2, alors l’horizon s’est agrandi, et le point P s’y trouve maintenant inclus. Un signal qui aurait été émis de P à t = 0 parvient enfin à l’observateur.
Tous les points sur le schéma qui sont à l’extérieur du cône sont causalement indépendants du point O. Aucun signal n’a pu être échangé entre eux et O. L’extérieur du cône représente les points de l’Univers non liés causalement à O. Ceci veut dire qu’un événement ne peut être la cause d’un autre que s’il a pu lui envoyer un signal pour le provoquer !
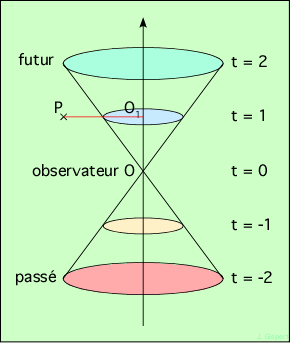
Lorsque l’Univers est devenu transparent (recombinaison), un signal de ce type est parti de tous les points de l’Univers, dans toutes les directions. Aujourd’hui, nous recevons ce signal depuis les points pas trop éloignés, qui constituent donc l’Univers observable. Supposons que le cercle rouge représente la recombinaison. A mesure que le temps passe, il s’éloigne de O le long de l’axe du temps (c’est O qui monte, entraînant son cône), et ce faisant, son diamètre augmente. Notre Univers observable croît donc au fil du temps.
Conisdérons deux événements A et B dans l’espace-temps. A est déterminé par une position (coordonnée horizontale) et par un temps (coordonnée verticale) ; B également. Toute ligne continue joignant A et B est une ligne d’univers. Nous allons préciser cela en considérant des exemples simples :
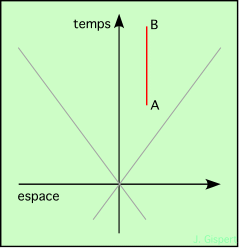
Première ligne : Elle décrit un objet immobile dans l’espace. Les événements A et B sont donc à la même coordonnée horizontale (puisque l’objet qui s’y trouve ne bouge pas). Mais le temps passe, donc la coordonnée verticale monte. L’objet ne bougeant pas dans l’espace, tous les points entre A et B sont aussi à la même coordonnée horizontale. Pour aller de A à B, il suffit d’attendre… Par conséquent, la ligne d’univers de cet objet est une ligne droite verticale. Il s’agit d’une ligne d’univers particulière de type temps (ou de genre temps), parallèle à l’axe du temps. |
 |
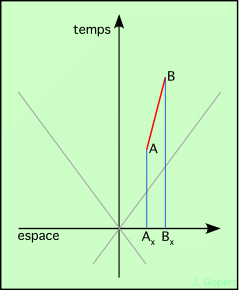
Deuxième ligne : Les événements A et B sont maintenant à des coordonnées horizontales différentes Ax et Bx, ce qui montre que l’objet se déplace. La ligne d’univers étant droite, le temps mis pour parcourir une distance infinitésimale d est le même partout. Donc la vitesse est constante. Par conséquent, un tel mobile se déplace de Ax à Bx à vitesse constante. Sa vitesse est inférieure à la vitesse de la lumière, puisque la pente de la trajectoire est inférieure à la pente d’un cône de lumière (qui représente justement la trajectoire d’un rayon lumineux). Cette ligne d’univers est également de genre temps. |
 |
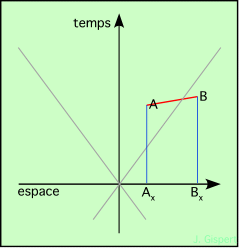
Troisième ligne : La pente de la ligne d’univers est plus forte que la pente du cône de lumière. Ceci montre que la vitesse du mobile est supérieure à la vitesse de la lumière. Aucun mobile connu ne se déplaçant à une telle vitesse, cette ligne d’univers n’a pas d’interprétation physique. On avait toutefois envisagé l’existence de particules qui se déplaceraient toujours à une vitesse supérieure à celle de la lumière. Elles étaient nommées tachyons. Pour elles, la surface du cône de lumière serait tout aussi infranchissable, mais elles vivraient à l’extérieur. On dit que cette ligne d’univers est de genre espace, car elle se trouve à l’extérieur du cône de lumière issu de A. |
 |
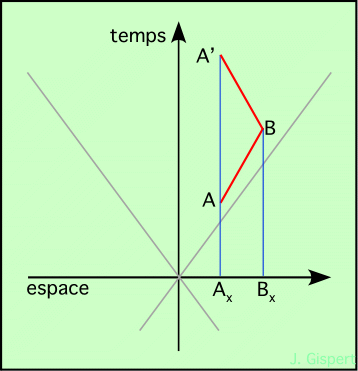
Quatrième ligne : On considère une ligne d’univers plus complexe, formée de deux segments de doite. L’interprétation de chacun des segments est claire (voir plus haut). La première ligne, de A à B, correspond à un déplacement du mobile de Ax à Bx, à vitesse constante positive (le mobile s’éloigne de l’origine dans le sens des x croissants). La seconde ligne représente le déplacement du mobile de B vers A′, A′ ayant la même position dans l’espace que A. Donc, le mobile revient à son point de départ. La vitesse est évidemment différente de celle de la première ligne, puisque maintenant le mobile se déplace dans le sens des x décroissants. La ligne d’univers composée est celle de l’un des deux jumeaux de Langevin. Celle de son frère est la ligne de genre temps qui relie A et A′. Cette ligne d’univers est de genre temps. |
 |
Bien évidemment, on peut construire des lignes d’univers plus complexes : nous n’avons considéré jusqu’ici que des déplacements à vitesse constante (avec un changement de vitesse brutal dans le dernier exemple). Si le mobile reste au repos, sa ligne d’univers est parallèle à l’axe des temps. S’il se déplace à vitesse constante, sa ligne est inclinée vers la droite si la vitesse est positive, vers la gauche sinon. La pente de la droite mesure la vitesse : pente nulle, vitesse nulle. Pente égale à celle du cône de lumière, vitesse de la lumière.
De ceci on déduit que, si un mobile accélère, la pente de sa ligne d’univers augmente ; s’il ralentit, elle diminue. On peut donc facilement interpréter une courbe quelconque.
Ligne quelconque : Sur ce nouveau schéma, on voit une ligne courbe, qui présente plusieurs variations. Partant de Ax (événement A) , le mobile accélère (la pente de sa ligne d’univers augmente, tout en restant inférieure à la pente du cône). Arrivé à mi-chemin de Bx, le mobile commence à ralentir (la pente diminue). Puis il arrive en Bx, et s’arrête (ligne droite verticale). Il stationne en Bx un certain temps (segment de droite vertical). Enfin, il repart vers Ax en accélérant, puis à mi-chemin ralentit, et arrive enfin à son point de départ Axavec une vitesse nulle (courbe tangente à l’axe vertical bleu). C’est une ligne d’univers assez générale de genre temps. |
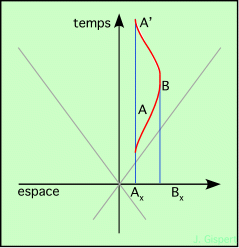 |
Une ligne d’univers représente donc bien le mouvement d’un mobile, avec la limitation à une seule dimension, puisqu’il n’est pas possible de représenter à plat une ligne d’univers en trois dimensions.
On va maintenant déduire une application très intéressante de cette représentation, et du formalisme qu’elle traduit.
Le principe d’inertie de Galilée dit : en l’absence de forces, un corps est soit au repos, soit en mouvement rectiligne uniforme.
Si le corps est au repos, sa ligne d’univers est une droite verticale. S’il est en translation uniforme (vitesse constante), sa ligne d’univers est aussi une droite, mais inclinée par rapport à la verticale, d’autant plus que sa vitesse est plus grande.
Si on raisonne dans l’autre sens , tout mobile dont la ligne d’univers est une droite,
se déplace en ligne droite dans l’espace,
et à vitesse constante,
donc est en translation (droite) uniforme (vitesse constante).
Le principe d’inertie de Galilée se réécrit donc ainsi :
Il n’y a plus de référence à la vitesse constante, celle-ci est contenue dans la rectitude de la ligne d’univers, qui amalgame l’espace et le temps !
Cette reformulation n’a l’air de rien, mais elle est fondamentale :
Une ligne d’univers non droite décrivant un mouvement accéléré (dernier schéma ci-dessus), l’idée de base de la Relatitvité Générale se trouve dans cette reformulation. Les lignes à considérer seront les géodésiques d’un espace-temps courbe.
La formule élémentaire d’addition des vitesses galiléenne ne peut être conservée, mais par quoi la remplacer ? La réponse est simple, il suffit de combiner les mouvements de trois référentiels (vu plus haut à propos du train) : R, que nous considérons au repos, R′ qui se déplace par rapport à R à la vitesse v1, et R" qui se déplace par rapport à R′ à la vitesse v2. En écrivant les transformations de Lorentz-Poincaré, et en les combinant, on aboutit à une formule, qui doit être de même forme que la transformation vue plus haut. Le référentiel R" se déplace par rapport au référentiel R à une vitesse v, qui est donnée par l’expression :
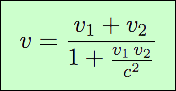
Là encore, si nous faisons tendre c vers +∞, nous voyons que le terme v1 v2 / c2 tend vers 0. Il reste alors la loi d’addition de Galilée. La loi d’addition relativiste n’en est donc qu’une généralisation, valable quelle que soit la vitesse.
Comme dans la théorie galiléenne, les deux vitesses considérées ici sont parallèles. Si ce n’est pas le cas, il faut effectuer les projections sur les trois axes.
Tout d’abord, l’expression "tout est relatif", qui a eu une grande vogue, dénote une profonde incompréhension de la Relativité. Bien sûr, le temps absolu n’existe plus, non plus que la longueur absolue. Mais la vitesse de la lumière est un nouvel absolu ! Et il existe toujours un temps au repos, et une longueur au repos. Nous avons vu que, quand on est en quasi-repos (vitesse petite devant c), les changements sont insignifiants, l’effet de perspective est négligeable. Il ne reste donc que le domaine des très grandes vitesses qui nécessite l’usage des formules relativistes.
La simultanéité de deux événements est une chose toute naturelle pour nous. Mais c’est une illusion…
Considérons deux événements qui ont lieu simultanément dans leur référentiel au temps t1 = t2, respectivement en x1 et x2 (x1 ≠ x2). En effet, dans la transformation de Lorentz-Poincaré, le temps se transforme par :
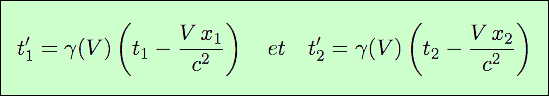
Le terme γ(V ) ne dépend que de la vitesse relative des référentiels ; il est donc de même valeur pour t′1 et t′2. Les deux événements étant simultanés dans R, t1 = t2. Pour savoir si les événements sont simultanés dans R′, calculons t′2 - t′1. Puisque t1 = t2 les termes correspondant s’annulent ; mais il reste les termes V x1 / c2 et V x2 / c2, qui sont différents puisque x1 ≠ x2.
Donc, dans R′, t′1 ≠ t′2, et les deux événements ne sont pas simultanés. Et puisque la différence entre t1 et t2 dépend directement de x1 et x2, on voit bien que c’est un effet de perspective.
La simultanéité des événements est donc un phénomène relatif, qui dépend du référentiel dans lequel on observe.
Là encore, si vous faites tendre c vers l’infini, vous constatez que les deux termes qui produisent la différence s’annulent. Les phénomènes sont perçus aux mêmes instants pour les deux observateurs. Dans notre expérience quotidienne, la vitesse de la lumière est bien trop grande pour que nous constations la relativité de la simultanéité, et nous avons bien l’impression que deux événements simultanés pour un observateur le sont aussi pour tous les autres.
La longueur propre d’un objet est, par définition, la longueur mesurée dans le référentiel où il est au repos. Par opposition, on nomme longueur impropre la longueur mesurée dans un référentiel en mouvement par rapport à l’objet mesuré.
Propriété 1 : γ(V ) est toujours plus grand que 1
V prend toutes les valeurs possibles de -c à +c. Lorsque V = 0, c’est-à-dire au repos, γ(V ) = 1, et tout se passe comme en Mécanique Classique. Tant que V reste petite, γ(V ) reste proche de 1 (très proche même). Ce n’est que lorsque V atteint des vitesses de l’ordre de quelques dizaines de pourcent de la vitesse de la lumière que γ(V ) commence à augmenter significativement, et modifie les résultats de manière mesurable. En fin, lorsque V tend vers ±c, γ(V ) tend vers l’infini.
Propriété 2 : γ(-V ) = γ(V )
Ceci est évident, puisque la vitesse n’intervient dans l’expression de γ que par son carré, qui est toujours positif.
Propriété 3 : Longueur impropre < longueur propre
Considérons une règle placée dans un référentiel R′ où elle est immobile, et alignée avec l’axe des x′. Sa longueur propre est l′, et les positions de ses extrémités sont x′1 et x′2.
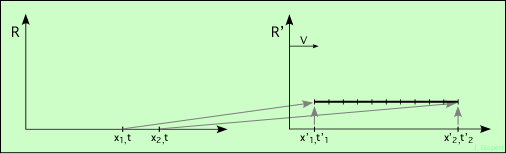
Dans le référentiel R′, la règle étant au repos, on peut mesurer les positions x′1 et x′2 à des instants t′1 et t′2 différents, puisque le résultat des mesures est indépendant du temps (la règle ne bouge pas). Par contre, si on se place dans le référentiel R, on voit la règle se déplacer. On peut y mesurer la position des extrémités de la règle, mais si on le fait à des instants différents, les mesures n’auront aucun sens, puisque la règle se sera déplacée entre les deux. Donc, il faut mesurer x1 et x2 au même instant t1 = t2. Dans ce référentiel, la longueur mesurée de la règle est notée l.
La longueur de la règle, dans tout référentiel, est égale à la différence entre les positions de ses deux extrémités. Dans R′, l′ = x′2 - x′1 = Δx′ ; dans R, l = x2 - x1 = Δx. Ecrivons les transformations de Lorentz-Poincaré relatives aux longueurs :
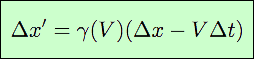
Puisque t1 = t2, Δt = 0. Donc il reste : Δx′ = γ(V ) Δx. On en tire :
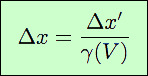
γ(V ) étant > 1 (V > 0), Δx est strictement plus petit que Δx′. C’est ce qu’on nomme contraction des longueurs.
La diminution de longueur est symétrique : R′ étant en mouvement par rapport à R, un observateur situé dans R′ voit une autre règle identique dans R raccourcie, dans la même proportion γ(V ). Ceci est parfaitement logique, si on se souvient que le repos n’existe pas. Dire que R′ se déplace à la vitesse V par rapport à R signifie simplement que la différence de vitesse des deux référentiels, par rapport à un troisième référentiel, est V. Vus de ce troisième référentiel, R et R′ peuvent parfaitement être tous deux en mouvement uniforme, donc jouer des rôles parfaitement symétriques. Donc, il serait invraisemblable de penser qu’ils puissent avoir un comportement différent.
La loi de contraction des longueurs a été trouvée en 1889 par Georges Fitzgerald. Il l’a publiée, mais malheureusement la revue a été suspendue pour des raisons financières. Elle a été retrouvée en 1892 par Hendrik Lorentz, qui l’a publiée. Plus tard, Lorentz a eu connaissance du travail de Fitzgerald, et l’a associé à sa découverte ! La loi de contraction des longueurs porte donc le nom de loi de Fitzgerald-Lorentz. Un bel exemple (rare) de fair-play (mot d’origine anglaise).
Notons que la vitesse est le rapport de la distance parcourue sur le temps de parcours, et que la vitesse de la lumière est invariable. Puisque nous avons vu plus haut une dilatation du temps, il est bien nécessaire, pour la compenser, d’observer une contraction des longueurs. Sans quoi la vitesse de la lumière serait variable…
Soit une fusée se déplaçant à la vitesse v par rapport à la Terre. Comment un observateur terrestre voit-il le temps (1 seconde) et les longueurs (1 mètre, dans le sens du mouvement) à bord de la fusée ? (on prend c = 300.000 km s-1)
|
|
On constate que pour les vitesses petites par rapport à c (bien que fort grandes pour nous), le facteur γ reste proche de 1, et longueurs et durées restent proches des valeurs mesurées dans leur référentiel. Même pour la vitesse de 150.000 km s-1, le temps mesuré n’est encore que de 1,155 s, ce qui est un accroissement encore faible. Le temps est doublé pour v = 259.807 km s-1. Ensuite, la progression s’accélère. Pour 0,999 c, soit 299.700 km s-1, le mètre ne mesure plus que 4,5 cm…
Dans les accélérateurs de particules, des vitesses encore plus proches de c sont atteintes. Ce tableau montre bien les problèmes que cela pose dans l’interprétation des résultats.
Tout d’abord, il faut préciser les termes employés : la masse d’une particule est définie au repos, et elle reste constante. Mais pour accélérer un objet, il faut lui communiquer une énergie croissante avec la vitesse : plus il va vite, plus il faut d’énergie pour l’accélérer. Lorsqu’on définit la loi fondamentale de la dynamique F = m γ, on se place dans le cadre classique, vitesses faibles devant c.
On généralise la notion de masse inerte en introduisant à sa place le coefficient d’inertie, fonction de la vitesse : F = I(v) γ. Il faudra calculer ce coefficient d’inertie.
Revenons provisoirement à la Mécanique Classique. Fermat a découvert le principe qui régit l’optique :
Il découle immédiatement de ce principe que dans un milieu homogène, les propriétés étant les mêmes partout, le plus court chemin (le plus rapide) est la ligne droite. Mais les lois de la réflexion et de la réfraction en dérivent directement aussi.
Ce principe s’illustre géométriquement pour la loi de la réflexion :
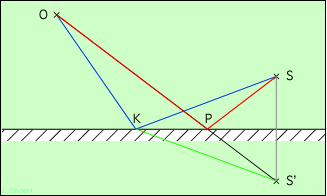
La source ponctuelle S émet un rayonnement dans toutes les directions. Un observateur situé en O voit l’image de la source dans le miroir. Quel est le chemin parcouru par la lumière pour faire le trajet ? La lumière pourrait a priori se réfléchir en un point quelconque du miroir. Mais le principe de Fermat nous dit que ce trajet doit être parcouru en un temps minimum, ce qui élimine tous les rayons possibles, sauf un. La lumière se déplace ici dans un seul milieu, homogène. Donc sa vitesse est la même partout. Par conséquent, le trajet le plus rapide est aussi le plus court. On voit bien que le trajet en bleu SKO est plus long que le trajet en rouge. Mais comment déterminer, parmi tous les trajets possibles, celui qui est le plus court ? Pour cela, dessinons le symétrique de la source par rapport au miroir, soit S ′. Il est évident que le plus court trajet de S′ à O est la ligne droite S′ O passant par P.
Mais puisque S′ est le symétrique de S par rapport au miroir, PS′ = PS. Donc SPO = S′ PO, et par conséquent SPO est minimum, donc parcouru dans le temps minimum. C’est la solution recherchée. Remarquez d’ailleurs que si vous regardez un objet dans un miroir, vous avez bien l’impression de le voir dans la position symétrique par rapport au miroir, ce qui confirme le calcul (on voit l’objet dans la direction d’où nous arrivent les rayons qu’il émet). Enfin, cette construction est utilisée en optique géométrique pour tracer le rayon réfléchi sur un miroir (la méthode s’applique aussi dans le cas d’un miroir non plan, en considérant la tangente à la surface au point de réflexion).
Insistons bien sur l’homogénéité du milieu : elle induit l’équivalence entre plus courte distance et plus court temps ! Dans le cas de la réfraction, il y a deux milieux différents, donc deux vitesses différentes. Alors, la distance la plus courte ne correspond pas avec le temps le plus court, et c’est ce dernier que le principe de Fermat impose (parce qu’il correspond à la réalité).Mais dans ce cas, il n’y a pas de construction géométrique possible.
On peut traduire le principe de Fermat de façon plus simple : la lumière prend toujours le chemin le plus rapide.
Un siècle plus tard (1744), Maupertuit définit un principe analogue en Mécanique, le Principe de moindre action. L’action est définie comme le produit de la masse, par la vitesse et par l’espace.
En utilisant ce principe, il suffira de chercher les évolutions qui minimisent cette variation pour obtenir la solution des problèmes mécaniques.
Nous pouvons maintenant en venir au coefficient d’inertie défini plus haut, et noté I(v). Le principe de moindre action s’applique en Relativité, à la condition de généraliser la définition de l’action. Alors, le coefficient d’inertie se détermine comme application de ce principe appliqué à l’action relativiste. La valeur obtenue est :
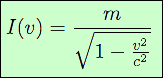
Lorsqu’un objet est au repos, sa vitesse est nulle, donc I(v) = I(0) = m (m est la masse mesurée au repos). Tant que la vitesse reste faible par rapport à c, le rapport v2∕c2 reste très proche de 0, et I(v) reste très proche de m. C’est ce qui justifie la Mécanique Classique. Mais lorsque v approche c, le rapport v2∕c2 tend vers 1, et le coefficient d’inertie tend vers l’infini ! Une particule qui se déplace à une vitesse proche de celle de la lumière présente un coefficient d’inertie très grand, qui s’oppose à son accélération.
C’est la raison pour laquelle il est impossible d’accélérer une particule de masse non nulle, à la vitesse de la lumière. C’est aussi ce qui explique que les accélérateurs de particules consomment tant d’énergie pour accélérer un malheureux électron… Lorsque sa vitesse approche celle de la lumière, son coefficient d’inertie, pour l’accélérateur qui est au repos, devient très grand. Il faut énormément d’énergie pour l’accélérer encore un peu.
La relation fondamentale de la dynamique étant valable pour les petites vitesses, il faut la conserver. Mais on y remplace la masse inerte par le coefficient d’inertie :
f = I(v) γ
Le coefficient d’inertie tendant vers l’infini lorsque la vitesse tend vers c, il en résulte qu’il est impossible d’accélérer une particule matérielle massive à la vitesse de la lumière.
Nous avons l’habitude d’une masse invariable. Lavoisier a pu dire « rien ne se perd, rien ne se crée, tout se transforme ». Mais regardons d’un peu plus près ce que cela signifie. « Rien ne se perd » veut dire que toute la masse que nous mesurons avant la réaction (chimique), se retrouvera après. « Rien ne se crée » constitue la réciproque : toute la masse que l’on trouve après la réaction y était forcément avant. « Tout se transforme » : les propriétés chimiques changent, donc à masse constante.
Nous allons voir qu’en fait ceci n’est pas vrai… Tout au moins, pas tout à fait. Lorsqu’on fait une réaction chimique, de la masse peut apparaître ou disparaître. Mais en faible quantité, de l’ordre de 10-8, ce qui est très difficilement mesurable, et ne l’était pas du temps de Lavoisier. Mais il s’agit là de réactions chimiques, les interactions entre atomes étant de type électromagnétique, à très faible énergie. Dans les réactions nucléaires, c’est l’interaction forte qui agit, et l’énergie de liaison est de l’ordre de 10-2, c’est-à-dire 1 %, ce qui est facilement mesurable. L’échange entre masse et énergie ne pouvait passer inaperçu lorsqu’on a commencé à réaliser des réactions nucléaires, alors que les réactions chimiques les cachaient parfaitement.
Le même principe variationnel que plus haut donne l’expression de l’énergie d’une particule en mouvement. Elle s’exprime par :
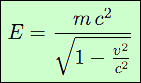
Si la vitesse est nulle, c’est-à-dire dans le référentiel de la particule, le rapport v2 ∕c2 est nul, le dénominateur vaut 1, et il ne reste que :
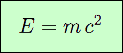
Relation bien connue !
Par l’égalité entre la masse et l’énergie (au coefficient c2 près), elle exprime que ces deux notions n’en font qu’une, qu’il y a équivalence entre elles. Par conséquent, l’une peut se transformer en l’autre, et c’est ce qui se produit dans le Soleil lorsqu’il transforme un peu de la masse d’hydrogène pour rayonner l’énergie qui nous fait vivre.
Pour mieux voir l’équivalence entre la masse et l’énergie, imaginons (comme les cosmologistes le font souvent) une nouvelle unité de longueur :
L’équivalence entre énergie et masse est évidente.
La Relativité Restreinte est donc une théorie de l’espace-temps, dans laquelle la vitesse de la lumière apparaît comme une constante liée à sa structure. Elle définit les relations entre deux observateurs galiléens, et toutes les conséquences qu’elles entraînent. Mais sa limite est dans ses prémices : seules les vitesses constantes sont traitées, et dès qu’il y a une accélération (changement quelconque de vitesse), elle trouve sa limite.
C’est dans cette limitation que se trouvent les justifications de la Relativité Générale…
Le temps se modifiant dans la transformation de Lorentz-Poincaré, doit maintenant faire partie intégrante de tout objet décrivant les lois de la physique. Prenons un exemple simple : en théorie classique, la vitesse est représentée par un vecteur à trois composantes, chacune correspondant à la projection de la vitesse sur l’axe correspondant. Puisque le temps est le même pour tous les observateurs, il est inutile de le représenter partout. Mais en Relativité, il faut l’adjoindre à chaque objet. Par conséquent, la vitesse, dans notre exemple, sera représentée par un vecteur à quatre composantes au lieu de trois.
Mais pour respecter le Principe de Relativité Restreinte, il faut que ces vecteurs puissent passer d’un référentiel galiléen à un autre. Donc, qu’ils se transforment comme les événements. On appelle donc quadrivecteur un vecteur à quatre composantes qui se transforme par la transformation de Lorentz-Poincaré.
Les noms des quadrivecteurs correspondant à des vecteurs de la théorie galiléenne sont constitués du préfixe quadri, accolé au nom du vecteur classique. Ainsi, on parle de quadrivitesse. Et puisque la vitesse est définie comme le rapport dx / dt, on remplace dx par ds, et dt par dτ (dτ étant la durée propre).
Sur l’ensemble des quadrivecteurs, on définit un produit scalaire semblable au produit scalaire habituel. Soient les quadrivecteurs V1 = (x1, x2, x3, x4) et V2 = (y1, y2, y3, y4) ; leur produit scalaire est V1 . V2 = x1 . y1 - x2 . y2 - x3 . y3 - x4 . y4. Remarquez les signes - à la place des sommes traditionnelles.
A partir de ce produit scalaire, on définit une pseudo-norme : || V ||2 = V . V = x12 - x22 - x32 - x42. Ce n’est pas une vraie norme, parce qu’elle n’est pas définie positive. Elle représente la longueur du quadrivecteur.
Le tableau suivant montre comment on définit trois notions relativistes à partir des notions classiques :
| Galilée | Einstein | ||
|---|---|---|---|
| vitesse | v = dx / dt | quadrivitesse | 4v = ds / dτ |
| accélération | a = dv / dt | quadriaccélération | 4a = d4v / dτ |
| quantité de mouvement | p = m v | quadrivecteur impulsion-énergie | 4p = m 4v |
Remarque 1: le quadrivecteur impulsion-énergie est noté parfois 4p = mc24v. Le facteur c2 peut être omis, si on considère un système d’unités dans lequel la vitesse de la lumière vaut 1.
L’adaptation de l’électromagnétisme est plus complexe, mais elle procède des mêmes méthodes.
Toute la Relativité Restreinte est ainsi notée dans le formalisme des quadrivecteurs.
Remarque 2 : la Relativité Restreinte n’est pas une réinvention des lois de la physique, mais seulement leur réécriture dans un formalisme plus général, élargissant leur domaine d’application. Cette réécriture met en évidence de nouvelles conséquences, qui ont toutes été validées par l’expérience.
Remarque 3 : considérant une onde électromagnétique dans son référentiel R′, et dans un référentiel considéré fixe R, on peut calculer, par l’application des transformations de Lorentz-Poincaré, l’expression de la fréquence dans les deux référentiels d’une part, et celle de l’énergie dans les deux référentiels d’autre part. Faisant le rapport, on trouve : E′ / ν′ = E / ν. Ceci quel que soit le référentiel R. Il en découle donc l’existence d’une constante, que l’on note h, telle que E = h ν. C’est la formule de Planck, qui est à la base de la Mécanique Quantique. On pourrait donc dire que la Mécanique Quantique est en partie issue de la Relativité, mais c’est en fait par des considérations expérimentales qu’elle a été fondée.
La Relativité Restreinte est associée au nom d’Einstein. Mais les choses sont un peu plus compliquées. Les problèmes de la Mécanique Classique ne faisaient plus de mystère pour les physiciens, et nombreux étaient ceux qui cherchaient comment en sortir.
Tout ceci ne doit pas diminuer les mérites d’Einstein, mais il faut admettre qu’il n’a pas bâti la Relativité Restreinte ex nihilo, comme on semble le croire souvent. Et qu’il a même profité du travail des autres physiciens pour le faire. Il est extrêmement difficile de lutter contre les idées admises pour avancer…
Pour de plus amples informations historiques sur la Relativité, consulter le destin de l’Univers, de Jean-Pierre Luminet.
Principe d’inertie : le principe d’inertie est conservé.
Le repos absolu n’existe pas : ceci n’est pas remis en cause, pas plus que l’inexistence de référentiel absolu.
Observateurs galiléens : constituent toujours le cadre de cette théorie, mais leurs vitesses ne sont plus limitées que pas celle de la lumière.
Principe de Relativité Restreinte : toutes les lois de la physique sont invariantes dans la transformation de Lorentz-Poincaré.
Le temps est relatif : le temps mesuré par deux observateurs galiléens dépend de leur vitesse relative.
Espace-Temps : le cadre de la théorie est maintenant l’espace-temps, combinaison des coordonnées d’espace et du temps.
Contraction des longueurs : les longueurs mesurées dans un référentiel en mouvement sont contractées dans le sens du mouvement.
Dilatation des durées : les durées mesurées dans un référentiel en mouvement sont dilatées…
Simultanéité : la simultanéité des phénomènes n’est plus qu’un souvenir. Elle dépend de la position de l’observateur dans l’espace-temps, c’est-à-dire de sa vitesse par rapport aux phénomènes observés.
Perspective : la relativité du temps et de l’espace est un phénomène de perspective, qui dépend de la position de l’observateur.
Transformation de Lorentz-Poincaré : elle remplace la transformation de Galilée. Elle définit à la fois les positions et le temps, puisque celui-ci est relatif à la vitesse des observateurs.
Vitesse limite : l’existence d’une vitesse limite dépend des propriétés de l’espace-temps, et non de celles de la lumière. Par conséquent, elle s’applique à toutes les interactions.
Composition des vitesses : découlant de la transformation de Lorentz-Poincaré, elle limite les vitesses possibles à une vitesse maximum, qui pourrait être celle de la lumière.
Métrique de Minkowski : la métrique mesure la distance entre deux événements. La métrique adaptée à la Relativité Restreinte est la métrique de Minkowski, généralisation du théorème de Pythagore.
Invariant : le ds2 est un invariant de l’espace-temps. Il est l’équivalent de la longueur dans l’espace physique. La transformation de Lorentz-Poincaré représente une rotation dans l’espace-temps, qui conserve les longueurs comme une rotation habituelle dans l’espace.
Electromagnétisme : cette théorie a été modifiée pour satisfaire au principe relativiste. Sous cette forme, elle est invariante dans la transformation de Lorentz-Poincaré.
Domaine d’application : La différence numérique sur les temps et les positions, entre la Relativité Galiléenne et la Relativité Restreinte, ne se fait sentir que pour des vitesses proches de celle de la lumière ; jusqu’à c / 10, elle reste très faible. Basée sur les repères galiléens, donc sans accélérations, elle ne concerne que les domaines où les forces gravitationelles sont négligeables. Donc dans un Univers pratiquement vide…
Relation fondamentale de la dynamique : f = I(v) γ.
La vitesse limite obtenue est la vitesse de la lumière, si le photon est de masse nulle. La masse du photon est extrêmement petite, mais il n’est pas sûr qu’elle soit strictement nulle. Si elle ne l’était pas, la vitesse de la lumière serait un peu inférieure à la vitesse limite. Pour l’instant, rien ne permet de supposer qu’elles diffèrent.
L’équivalence des observateurs galiléens implique que les transformations permettant de passer d’un référentiel galiléen à un autre forment un groupe. Cette propriété, avec l’isotropie de l’espace, permet de construire la transformation de Lorentz. Equivalence des observateurs galiléens et isotropie de l’espace-temps fondent la Relativité Restreinte.
La Relativité Restreinte explique de nombreux phénomènes, autrement incompréhensibles (durée de vie du muon, du pion…).
La Relativité Restreinte ne tient pas compte des accélérations. C’est sa limitation, qui nécessite une nouvelle théorie : ce sera la Relativité Générale.
---=OO=---