L’actualité du LAM	Le cours à l’Observatoire Historique de Marseille	… …	liens - alphabet grec bibliographie fiches lexique multiplicateurs tableau périodique	Mis à jour le 18/08/17
Dégénérescence

La dégénérescence est un état de la matière, qu’on rencontre dans le cœur de certaines étoiles, et dans certaines phases de leur vie.

Considérons d’abord le cas dans un cadre de Mécanique Classique.

Au zéro absolu, tous les électrons ont la même vitesse nulle.

Si on augmente légèrement la température, les électrons sont mis en mouvement, mais ne peuvent se déplacer vite, puisque leur vitesse moyenne mesure la température. Donc les électrons se partagent la faible énergie disponible, et ont tous la même vitesse (donc la même impulsion).

Plus on augmente la température, plus on augmente la vitesse moyenne des électrons. Mais l’espace de répartition entre 0 et cette vitesse moyenne est de plus en plus grand. Donc les électrons vont se répartir dans cet espace croissant. Lorsque la température est très élevée, ils se répartissent presque uniformément. Par conséquent, le nombre f(p) d’électrons en fonction de la vitesse (de l’impulsion), montre un maximum marqué à basse température, et ce maximum devient de plus en plus flou lorsque la température augmente. Ceci se voit sur le schéma ci-dessous :

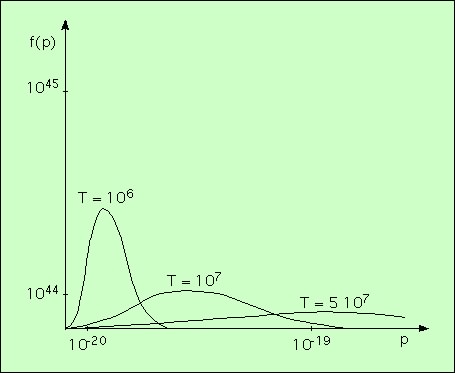
Ce schéma montre que, pour 10⁶ K par exemple, le nombre d’électrons ayant une impulsion de 10^-20 est très grand. Imaginez que la matière soit très condensée, soumise à une densité élevée. Alors, les électrons seront très proches les uns des autres. S’ils ont des impulsions identiques (vitesses identiques), ils seront à la fois au même endroit et à la même vitesse, ce que le principe d’exclusion de Pauli interdit.

A une position et une impulsion données, il ne peut y avoir que deux électrons, de spins opposés. Ceci limite donc le nombre d’électrons ayant une impulsion donnée. Il est facile de montrer que ce nombre doit être inférieur à 8 π p² / h³. On peut ajouter au graphique précédent la courbe qui représente cette fonction. La variation étant proportionelle à p², c’est une parabole :

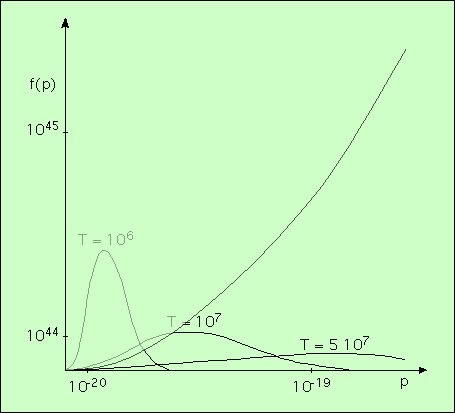
Le principe de Pauli impose donc que le nombre d’électrons soit inférieur à la valeur de la parabole, donc en-dessous de celle-ci.

On voit ainsi que tout se passe bien pour une température élevée (5 10⁷ K), mais que pour une température bien plus basse, le principe d’exclusion est violé par cette approche classique.

Tout ceci a été calculé à densité constante. Si on augmente la densité, les électrons se rapprochent, et le principe de Pauli est d’autant plus violé.

La mécanique quantique nous indique que, dans ces conditions, les électrons vont peupler tous les niveaux d’énergie en-dessous d’une certaine valeur nommée énergie de Fermi. La répartition classique des vitesses ne s’applique plus, et les électrons prendront une vitesse supérieure à celle calculée plus haut. Cette vitesse accrue implique une pression plus grande, dite pression de dégénérescence.

Lorsque les électrons peuplent tous les niveaux bas d’énergie, on dit qu’ils sont dégénérés.

Les considérations ci-dessus montrent que le taux de dégénérescence augmente si :

•  la température baisse ;
•  la densité augmente.

---=OO=---